大气边界层大涡模拟入口湍流生成方法综述
周 桐,杨庆山,闫渤文,Pham Van Phuc,王京学
(1.北京交通大学土木建筑工程学院,北京 100044;2.结构风工程与城市风环境北京市重点实验室,北京 100044;3.重庆大学土木工程学院,重庆 400044;4.清水建设技术研究所,日本,东京 135-8530)
现场实测、理论分析和风洞试验是结构风工程的三种传统研究方法。随着计算流体动力学方法(Computational Fluid dynamics,简称CFD)的不断改进和计算机软硬件水平的飞速发展,CFD成为结构风工程研究的重要工具,并逐渐发展成为一个重要分支,被称为计算风工程(Computational Wind Engineering,简称 CWE)。雷诺平均法和大涡模拟是计算风工程的两种主要求解方法,其中大涡模拟是一种对大于网格尺度的湍流脉动进行直接模拟,而对小于网格尺度的湍流脉动采用亚格子模型来描述的非稳态模拟方法。大涡模拟作为一种兼顾求解精度和求解效率的数值模拟方法,正逐渐成为结构风效应数值模拟研究的主要选择[1-3]。城市大气边界层研究涉及的尺度通常可划分为城市尺度(宏观尺度)、小区尺度(中尺度)和街区尺度(微尺度),而不同尺度上的大气运动呈现出不同的空气流动特点[4],因此需要发展适用于不同尺度特征的大气边界层数值模拟入口生成方法。例如,针对小区尺度的大气微环境研究,由于同时受到较大尺度气象因素和小尺度湍流脉动的影响,其入口来流特性应具有显著的多尺度特性,需采用多尺度耦合模拟[5-7]。而本文主要关注的是近地大气边界层内的结构风效应,需要模拟的主要是小尺度湍流脉动对结构表面的脉动风压分布和结构周围的绕流特性[8],因此真实重现目标风场内的小尺度湍流脉动特性是采用大涡模拟准确评估结构风效应的重要前提。然而,如何合理定义大涡模拟的入口边界条件一直都是计算风工程研究领域关注的重难点问题[9]。理想的结构风效应大涡模拟入口边界条件应满足以下四点要求:1)正确重构表征大气边界层风场的主要统计量,包括平均风速剖面、湍流强度、脉动风速功率谱和湍流积分尺度等;2)具有与真实风场相接近的流场结构;3)生成的脉动风速具有随机性;4)适用于并行计算环境,并且计算成本较低。
预前模拟法和人工合成法是目前主要的两类大涡模拟入口湍流生成方法。然而,由于缺乏从结构风工程研究的角度对不同方法的特点以及适用性进行系统探讨,研究人员难以合理选择和正确应用大涡模拟入口湍流生成方法开展结构风工程问题的研究。本文首先综述了不同方法的基本原理,梳理其在结构风工程领域的应用和发展,对比分析不同方法的特点及适用性,为基于大涡模拟方法开展结构风工程问题的研究提供了重要的理论指导。
1 预前模拟法
在预前模拟法中,求解的计算域包含两部分:主计算域和辅助计算域。首先在辅助计算域生成满足大气边界层风场特性的稳定来流,然后将其作为主计算域的入口边界条件。由于辅助计算域内生成湍流的具体方式不同,预前模拟法主要有两种实现形式,分别是被动模拟法和“回收-变换”法。
1.1 被动模拟法
在建筑结构风洞实验中,尖劈、粗糙元等装置被广泛应用于模拟不同地貌类别的大气边界层风场。采用风洞试验的被动模拟技术,通过建立尖劈、粗糙元的数值风洞模型,并在入口边界赋予与风洞试验相接近的均匀来流,进而一定程度上再现风洞试验中模拟的大气边界层风场,如图1所示。 被动模拟法的基本思想易于理解,并且技术难度较低,因而被研究人员应用于生成结构风效应大涡模拟的目标风场[10-12]。然而,这种方法在实际应用时主要存在以下两点局限性:1)工作效率低。不同的目标风场对应于不同的风场布置,因此在模拟不同目标风场条件下的结构风效应前,需要调整数值风洞中尖劈、粗糙元的几何形状和几何位置,并重新划分网格。2)计算成本高。计算域内的网格分辨率很大程度上决定了采用被动模拟法生成的大气边界层风场是否与风洞试验结果相一致。

图1 被动模拟法数值模型Fig.1 Numerical model of the passive simulation method
为解决上述不足,Enoki和Ishihara[13]提出了在计算域中建立“隐性粗糙元”的方法,即通过在动量方程中添加阻力源项,以近似地模拟粗糙元对来流产生的拖曳力效应。

式中:Cf=CD,ui/(1-γ0)2,CD,ui为阻力系数,建议取值为0.4[14];γ0=V0/Vgrid,γ0为体积占有率,V0为粗糙元体积,Vgrid为包含粗糙元的网格体积;l0=V0/A0,l0为特征长度,A0为单个粗糙元的迎风面积。
在此基础上,Liu等[15]将其延伸应用于光滑三维小山和二维山脊周围湍流场的大涡模拟。这种方法避免了在辅助计算域内建立数值粗糙元模型,当目标风场对应的粗糙元的几何尺寸、排列形式发生改变时,可通过修改相关程序代码快速地进行调整,有效地提高了工作效率。然而,该方法难以描述尖劈对于风场的影响。
1.2 “回收-变换”法
基于湍流边界层的相似变换理论,“回收-变换”法将提取得到的湍流边界层下游的平均统计量和脉动统计量进行调节后作为计算域的入口边界条件。这种方法最初应用于低雷诺数平板湍流边界层[16],并不适用于土木工程结构所处的高雷诺数粗面湍流边界层。为适应结构数值抗风研究的需求,在Lund等[17]方法的基础上,Nozawa和Tamura[18]在入口平面和循环站间建立数值粗糙元并合理地调整速度缩尺函数,实现了粗糙壁面湍流边界层的模拟,然后将其作为低矮建筑结构风效应大涡模拟的入口边界条件。通过引入边界层厚度沿顺流向不发生变化的假设,Kataoka[19]简化了Lund等[17]提出的拟周期边界条件,将下游循环站的脉动风速分量缩尺后与入口平面的平均风速分量叠加:

式中:u、v、w分别为顺风向、横风向和竖向的瞬时风速;分别为顺风向、横风向和竖向的平均风速;下标inlt表示入口平面;下标recy表示循环站;φ(θ)为权函数。
为进一步模拟具有较高湍流强度的大气边界层风场,基于 Kataoka[19]提出的简化方法,朱伟亮和杨庆山[20]通过建立数值粗糙元和扰流杆模型增大了近地面和边界层高处的湍流强度,如图2所示。

图2 “回收-变换”法数值模型Fig.2 Numerical model of the recycling-rescaling method
由于主计算域和辅助计算域的粗糙度存在显著差异,来流的湍流强度在主计算域内会发生一定程度的衰减,尤其是边界层高处。王婷婷和杨庆山[21]通过在一定高度以上添加满足正态分布的随机数,提高了边界层高处的湍流强度,但其风速时程呈现出明显的周期性,因此生成的流场特性与真实大气边界层风场不符。Aboshosha等[22]采用随机傅里叶模式生成分形表面,以模拟任意粗糙壁面的湍流边界层。Li等[23]提出了基于脉动速度比例系数λ(z,t)的主动控制方法,以生成满足目标湍流强度特性的边界层。

式中:Iu,obj(y,z,t)为目标湍流强度;Iu,re(y,z,t)为瞬时湍流强度;为横向平均值;为循环站处的平均速度;N为模拟时间步数;Δt为时间步长。
提高生成目标湍流的效率并避免虚假低频脉动的产生对于“回收-变换”法在结构风工程领域的应用具有重要意义。Liu和Pletcher[24]通过动态变换循环站的位置,使循环站处的湍流充分发展,有效减少了生成目标湍流的时间;Jewkes等[25]采用镜像方法有效地避免了入口边界和循环站间的误差反馈和累积,缩短了计算域长度,从而降低了计算成本;Stevens等[26]通过实时将辅助计算域出口区域内的数据传输到主计算域,提高了求解效率。Spille-Kohoff和 Kaltenbach[27]采用在计算域入口边界与循环站间添加源项的方法,对流场进行有效的反馈控制,降低了人工速度场长时间相关形成虚假低频脉动的可能性;Morgan等[28]将动态变换的横向反射应用于循环站,从而避免虚假低频脉动的产生。
2 人工合成法
人工合成法是基于严格的数理推导构造满足大气边界层风场特性(平均风速剖面、湍流强度、脉动风速功率谱等)的入口边界条件。根据生成湍流脉动的具体方式不同,人工合成法主要分为四类,分别是谱合成法、本征正交分解重构法、数字滤波法、涡方法。
2.1 谱合成法
基于对频谱空间和波谱空间的随机傅里叶变换,谱合成法可分为传统的谐波合成法和傅里叶合成法两类。
2.1.1 谐波合成法
谐波合成法是利用脉动风速的目标功率谱密度和空间相关性在频域内构造含有高斯随机系数项的三角级数,脉动风速样本可以表达为一系列的正弦和余弦函数。

式中:Δω为频率增量,Δω=(ωmax-ωmin)/N1;N1为采样频率点数,理论上N1→∞;Hjm(ωml)为目标功率谱S(ωml)的Cholesky分解矩阵H(ωml)中的元素;φml为均匀分布于[0,2π]的随机相位角。
Rice[29]首先提出了谐波合成法的基本思想,但是其仅适用于一维单变量平稳高斯随机过程,无法模拟大气边界层风场中不同位置处的脉动风速时程。经过Shinozuka等[30-32]的改进,将谐波合成法发展到多变量、非平稳高斯过程的模拟,进而适用于生成真实的随机脉动风场。基于频率双索引的概念,Deodatis[33]提高了谐波合成法的求解精度,模拟了各态历经的多变量平稳高斯随机过程。李正农等[34]采用非均匀圆频率间隔的方法有效地解决了以往谐波合成法模拟的周期性问题。上述方法改善了模拟精度,但是却降低了模拟效率。采用谐波合成法生成大涡模拟脉动入口边界时,通常需要模拟入口平面多点的脉动风速时程,而随着模拟点数的增加会导致其计算效率的显著降低[35],因此提高其求解效率至关重要。由于谐波合成法求解过程涉及对复杂矩阵进行大量的 Cholesky分解以及三角级数叠加,因此Cholesky分解与三角级数的叠加是制约其计算效率的主要因素。Yang[36-37]采用快速傅里叶变换技术简化了三角级数的叠加,进而大幅度提升了谐波合成法的模拟效率。孙瑛等[38]基于本征特征正交分解技术,建立能够近似代表实际风场频谱特性的少量阶时间主坐标的互谱密度矩阵,在保证计算精度的前提下提高了计算效率。Ding等[39]将脉动风速的互谱密度矩阵简化为实对称矩阵,利用三次Lagrange插值方法减少了Cholesky分解的次数,进而缩短了计算时长。罗俊杰和韩大建[40]引入并改进基于矩阵分块的“递归”算法以提高Cholesky分解效率,并采用矩阵乘法取代了效率低下的叠加算法。李春祥和刘晨哲[41]利用径向基神经网络对Cholesky分解后的互谱密度矩阵进行插值,在保证谐波合成法模拟精度的同时,显著地提高了模拟效率。Huang等[42]采用相位分解,将演化功率谱密度矩阵/功率谱密度矩阵转换为实模矩阵,进而提高了Cholesky分解效率。基于双索引频率和谱分解矩阵的特点,祝志文和黄炎[43]提出在双索引频率轴向采取均匀分布插值,谱分解矩阵的频率轴向采取前密后疏分段插值能够大幅提高随机脉动风场的模拟效率。对于Cholesky分解矩阵的非对角线元素,采用三次Lagrange插值方法的模拟值在某些插值区间存在较大波动。因此,陶天友和王浩[44]提出了基于Hermite插值方法的谐波合成法,以兼顾模拟精度和计算效率。
谐波合成法具有严格的数学理论基础,并且模拟的脉动风速功率谱与脉动风速的自/互相关函数均能够与目标值吻合较好。然而,由于其生成的脉动风速时程无法严格满足连续性条件,因此会在计算域内产生虚假的压力脉动并可能导致计算过程的发散。同时,由于该方法无法独立生成不同空间点的脉动风速时程,且生成的风速时程数据需要预先储存,因此不适用于并行计算。
2.1.2 傅里叶合成法
傅里叶合成法是基于三维能量谱在波数域内生成与目标功率谱相一致的、空间相关的湍流场。

Kraichnan和 Robert[45]首先提出了傅里叶合成法的基本思想,但其仅适用于生成均匀、各向同性的湍流场。以Kraichnan和Robert[45]提出的算法为基础,Smirnov等[46]引入了湍流长度尺度和时间尺度,并通过比例和正交变换生成了非均匀各向异性的湍流场。然而,采用上述方法仅能生成满足高斯谱形式的湍流场,并不适用于结构抗风研究。然而,通过改变的分布形式可以模拟具有不同能量谱特性的脉动速度场。当各向同性地分布在半径为k0的空间球面或平面圆表面时,对应脉动速度场的能量谱分别为利用E1(k)和E3(k)仅在k0处不为零的特性,以构造满足任意能量谱的脉动速度场:

式中:km为波长值;M为能量谱离散的区间样本数。基于上述理论,Huang等[47]提出了 DSRFG(discretizing and synthesizing random flow generation)方法,其脉动速度场的表达形式为:


在结构风工程领域,DSRFG方法主要具有以下几点优势:1)严格满足连续性条件;2)生成的湍流场基本满足脉动风速功率谱;3)能够独立生成不同空间点的脉动风速时程,适用于并行计算。然而,DSRFG方法中的Ls取值并未考虑其与相干函数的内在联系。基于数学推导,Castro和 Paz[48]指出采用DSRFG方法生成的随机脉动风场的湍流强度与离散谱的区间样本数相关。当离散谱的区间样本数达到一定数量时,湍流强度的模拟值能够较好地吻合目标值。在 DSRFG方法的基础上,Castro和Paz[48]通过时间尺度参数τ0的引入来考虑脉动风速的时间相关性。
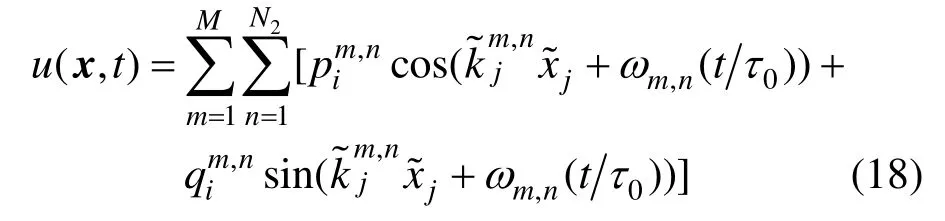
脉动风的空间相关性对于准确评估柔性结构(高层建筑、高耸结构、大跨度桥梁等)的风致耦合作用十分重要,Aboshosha等[49]在 DSRFG方法的基础上,提出了 CDRFG(consistent discretizing random flow generation)方法。这种方法修正了脉动风速谱能量在频率上的分布,并且通过建立空间尺度参数与频率的关系,比较合理地考虑了脉动风的竖向相关性。

式中:C为相干函数衰减系数;D=0.5~1.0h;h为建筑高度。类似于DSRFG方法,为使生成的脉动速度场满足连续性条件,须满足下列方程:

由于DSRFG方法、CDRFG方法需要耗费较多的计算资源并且脉动风速的表达形式相对复杂,因此,Yu等[50]在DSRFG方法、CDRFG方法的基础上,通过窄带过程的模拟和叠加,并考虑三个方向上脉动风的空间相关性提出了表达形式更为简洁、严格满足连续性条件和脉动风速功率谱的 NSRFG(narrow-band synthesizing random flow generation)方法。

式中:ui(i=1,2,3)为顺风向、横风向和竖向的脉动风速;N3为功率谱离散数目;Si(fn)(i=1,2,3)分别为顺风向、横风向和竖向的脉动风速功率谱;fn=( 2n-1)Δf2,Δf为带宽;φn~U(0,2π);为使生成的脉动速度场满足连续性条件,须满足下列方程:

从空间解析几何的角度分析,上述方程为一空间圆曲线,因此ki,n(i=1,2,3)可由式(25)求解:

2.2 本征正交分解重构法
本征正交分解法是一种随机脉动风场的高效描述方法[51-52],仅需通过少量阶与时间主坐标和空间本征模态的级数组合来重构随机脉动风场的主要信息[53-55]。
式中:a(n)(t)为时间主坐标;ψ(x)为本征模态;n为所选本征模态阶数。
基于热线风速仪或粒子图像测速仪采集得到平面内各点的脉动风速时程的本征正交分解,结合随机模拟技术,理论上可以构造出满足风洞流场特性的入口边界条件。热线风速仪具有较高时间分辨率,但由于热线风速仪同步测量的空间点数量有限,因此其空间分辨率较低。对此,Druault等[56]采用线性随机估计填补了测量位置间的空缺信息,进而生成了大涡模拟的入口边界条件。然而,线性随机估计的准确性很大程度上取决于空间点的距离。相比于热线风速仪,粒子图像测速仪具有较高空间分辨率。因此,Perret等[57-58]通过对三维粒子图像测速仪的测量数据进行本征正交分解,进而生成了空间发展平板混合层大涡模拟的入口边界条件。然而,由于其采样频率相对较低,因此需要引入随机时间序列来提高时间分辨率。
采用本征正交分解重构法生成的入口湍流需要经过较长的发展距离才能演化成为真实湍流,Johansson和Andersson[59]基于本征正交分解法准确定位具有最多能量的模态,并通过纳维-斯托克斯方程的伽辽金映射,将低能量、小尺度的模态叠加到高能量、大尺度的模态上以平衡耗散水平,实现了速度分量间更加真实的能量分布。
2.3 数字滤波法
数字滤波法的基本思想是利用数字滤波器将离散随机序列转变为满足指定时空相关性的随机序列。

式中:N5为滤波器的长度(),Δx为网格尺寸,l为湍流积分尺度;rm为满足零均值、单位方差的随机序列;bj为滤波系数,其表达式为。
随机序列的时间相关性同样可采用指数函数来定义:

式中:C为常数(π/4);T为拉格朗日时间尺度,T=l/Ucon,Ucon为平均对流速度。
基于数字滤波法生成的瞬时速度场为:

式中:Ui为平均速度;aij为雷诺应力Rij的Cholesky分解[17]。

Klein等[60]首先提出了数字滤波法的基本思想,指出采用该方法能够再现目标湍流场的二阶统计量和自相关性,但是其计算效率受限于网格形式。Kempf等[61]基于并行算法程序的改进,使其在复杂的非结构化网格形式下仍然具有较高的计算效率。Xie和 Castro[62]提出了简化的滤波方法,在每个时间步内仅需要进行二维滤波,因此进一步地提高了该方法的计算效率。同时,该方法是易于并行的,但其生成的湍流场无法严格满足零散度条件,因此会在计算域内引起显著的压力脉动,进而无法准确评估结构上的瞬时风荷载(极值)。为避免虚假的压力脉动,Kim等[63]改进了不可压缩流动求解器中的速度-耦合程序,Daniels等[64]将其应用于评估高层建筑物的极值风荷载和表面脉动压力。采用数字滤波法生成的湍流场通常无法与纳维-斯托克斯方程相容,导致其入口的湍流特性无法在计算域内得到良好的保持,然而,结构风工程领域主要关注建筑物附近的来流湍流特性。为满足结构数值抗风研究的需要,Lamberti等[65]在Kim等[63]方法的基础上,以建筑物区域的湍流特性为目标,采用梯度优化算法来确定入口湍流生成程序中的输入参数。该方法的基本步骤可简要概括为以下两步:1)基于贝塞尔曲线拟合目标湍流特征统计量(如雷诺应力、湍流积分尺度等)剖面;2)基于标量化技术确定目标函数(以雷诺应力为例)。

式中:yp为贝塞尔曲线控制点p的高度;γu、γv和γw为权重因子;下标i、b和exp分别表示入口平面、建筑物和风洞实验的雷诺应力值。
2.4 涡方法
基于涡量的拉格朗日描述,二维涡方法(VM)在入口平面构造随机分布的涡以产生湍流脉动。

式中:N6为入口平面的涡数量;Γi为涡环通量,为入口平面的面积;k为湍流动能;x为每个涡的二维坐标;xi为每个涡中心的二维坐标;z为顺流向的单位矢量;σi为涡的特征尺度。
基于湍流混合长假设,Mathey等[66]将局部涡的特征尺度与入口平面的湍流动能和湍流耗散率相联系(),并采用简化的线性运动学模型来描述顺流向的湍流脉动。在结构风工程领域,湍动能和耗散率通常采用下述公式进行计算:

在二维涡方法的基础上,Jarrin等[67-68]提出了SEM(synthetic eddy method),采用形函数来定义具有时空相关性的三维涡旋相干结构,进而生成脉动速度场。

式中:Ui为顺流向的平均速度;N7为入口平面的涡数量;aij为雷诺应力Rij的Cholesky分解;为独立随机变量,在(-1,1)上服从均匀分布;xk为涡的空间位置坐标;fσ(x-xk)为xk位置处涡的速度分布函数。

式中:f为形函数,常见的包括三角函数、高斯函数等;σ为涡的特征尺度,由湍动能、耗散率、网格尺度共同决定。

式中:κ=0.41;Δ=m ax(Δx,Δy,Δz);δ为边界层厚度。
基于泰勒湍流冻结假设以定义脉动速度场的时间相关性,在每个迭代时间步内的第k个涡的空间位置为:

式中,Uc为平均速度。
基于上述合成涡方法能够生成满足部分大气边界层风场特性的湍流场,如平均风速剖面、湍流强度、湍流积分尺度、时空相关性。同时,其各点风速时程的生成过程独立,因此适用于并行计算。然而,由于其生成涡的特征尺度单一,因此不符合脉动风速功率谱特性。针对这一问题,Luo等[69]提出了 MSSEM (multi-scale synthetic eddy method),其基本思想是合成具有不同频谱能量的多尺度涡以构造满足任意脉动风速功率谱特性的湍流场。

式中:U(x)为顺流向的平均速度;M为涡的特征尺度的数量;Nm为m阶尺度涡的数量,其定义式为为a的m阶分量,其中a为雷诺应力的 Cholesky分解,其定义式为为随机3×3矩阵,在(-1,1)上服从均匀分布;为位置处的速度分布函数。

基于不同尺度涡之间的独立性假设,方向i上的脉动速度功率谱可表示为:

式中:n为频率;为与m阶尺度涡相关的脉动速度功率谱。

式中,Fi为形函数f的傅里叶变换。
相应地,无量纲化的脉动速度功率谱为:

结合式(42)~式(45)可得:

Luo等[70]采用MSSEM生成了满足大气边界层风场特性的脉动入口边界条件,进而运用大涡模拟比较准确地评估了高层建筑上的风压分布和风荷载特性。
3 结论
生成满足大气边界层风场特性的入口边界条件是合理运用大涡模拟开展结构风工程研究的关键瓶颈问题。本文对预前模拟法和人工合成法这两类大涡模拟入口湍流生成方法的基本原理和发展历程进行综述,并从结构风工程研究的角度对不同方法的特点及适用性进行对比分析,结果表明:
(1)采用预前模拟法生成的入口边界条件具有相对真实的流场结构与时空相关性。同时,由于其满足流体运动的基本方程(连续性方程、纳维-斯托克斯方程),因此入口湍流特性在计算域内能够得到良好的保持,并且数值计算易于收敛。然而,预前模拟法无法直接定义目标湍流特性(湍流强度、湍流积分尺度和脉动风速功率谱),调试过程相对复杂。当网格质量和网格分辨率足够高时,运用被动模拟法能够比较真实地再现大气边界层风洞的流场特性。然而,被动模拟法需要在主要计算域外增加额外的预前模拟计算域,网格量增加较多,从而降低了工作效率、提高了计算成本,另一方面,要求主要计算域边界形状规则,这两点在一定程度上限制了其在结构风工程领域研究中的应用。基于“回收-变换”法生成的入口边界条件满足大气边界层的平均风速剖面,其局限性主要体现在边界层的湍流强度较低,与近地脉动风场的高湍流度特征不符。为适应结构数值抗风研究的需求,通常采用前置粗糙元法来增大近地面的湍流度,但边界层高处的湍流度仍然低于目标值。在“回收-变换”法的基础上,结合基于脉动速度比例系数的主动控制方法,在一定程度上能够生成满足目标湍流强度特性的大气边界层风场。
(2)采用人工合成法生成的入口边界条件满足大气边界层风场特性与时空相关性。同时,该方法的计算效率较高、适用范围较广。由于人工合成湍流无法满足纳维-斯托克斯方程,需要在计算域入口边界与计算模型之间预留较长的发展距离来形成目标湍流,而在此过程中,湍流特性可能因数值模型、网格尺寸、时间步长等因素发生改变。基于谐波合成法能够生成满足任意目标谱特性和空间相关性的脉动入口边界,但由于其无法与连续性方程相容,会在计算域内引起显著的压力脉动,进而无法准确评估结构的瞬时风荷载。谱合成法中的DSRFG、CDRFG和NSRFG方法严格满足连续性条件,入口湍流的空间相关性可通过空间尺度参数调整,其中NSRFG方法的并行计算效率相对较高。本征正交分解重构法的应用很大程度上取决于是否具有类似大气边界层湍流风场的实验数据,因此其在结构数值抗风研究中存在较大的局限性。数字滤波法生成的入口边界无法满足纳维-斯托克斯方程,因此入口湍流特性无法在计算域内得到良好的保持。相比于谱合成法、本征正交分解重构法和数字滤波法,涡合成法生成的入口湍流能更快地发展成为真实湍流。其中,MSSEM 生成的湍流场能较好地满足脉动风速功率谱,进而更适用于结构风工程研究。结合大涡模拟入口湍流生成方法在结构风工程领域的研究现状,对后续研究作出以下几点展望:
(1)在“回收-变换”法的基础上,进一步发展多目标湍流特性(湍流强度、湍流积分尺度等)的主动控制技术,提高“回收-变换”法的调试效率。
(2)人工合成法生成的入口湍流特性可能无法在计算域内较好地保持,结合相关优化算法对人工合成湍流程序中的输入参数进行适当调整,使来流在感兴趣的研究区域具有目标湍流特性。
(3)在满足大气边界层主要统计特性(平均风速剖面、湍流强度和脉动风速功率谱)的前提下,运用人工合成法生成比较合理的大气边界层湍流结构,即旋涡尺度随高度的增加而增加,并且随地面粗糙度的增加而减小。
(4)来流湍流特性会显著影响结构表面的风荷载特性,并且不同结构(高层建筑、低矮建筑、大跨度屋盖结构等)风荷载特性具有显著差异,因此应进一步对比各种入口湍流生成方法在不同结构风效应大涡模拟研究中的适用性。

