基于贝叶斯公式的采矿方法优选模型

王丹华 路增祥，2

（1.辽宁科技大学矿业工程学院，辽宁鞍山114051；2.辽宁省金属矿产资源绿色开采工程研究中心，辽宁 鞍山114051）

目前，由于全球经济复苏和我国矿业经济政策的影响，矿业投资活动增强，全球矿业预计6～8 a 后实现全面复苏［1］。充分利用资源，统筹规划，在确保矿山安全的前提下实现对资源的综合开发利用，扩大矿山规模，以最少建设投资和经营成本，获取最佳的经济效益，是矿产资源开发企业所追求的目标。采矿方法选择是影响矿山企业经济效益和安全生产的重要因素［2-4］，必须慎重选择［5-8］。传统的采矿方法常由相关专家采用经验类比法进行优选，这种方法主观性强，不具有完全适用性。目前，常采用定量分析或定性分析的优选方法，建立评价模型，获取指标的合理权重，从而获得指标综合评价值，指标综合评价值越大，方案越优。目前，在优选实践中常采用的方法有层次分析法［9-10］、模糊数学法［11］、组合赋权与TOPSIS 法［12］、模糊聚类与BP 神经网法［13］以及其它多种方法综合的优选方法［14-16］。郭进平等［17］采用AHPTOPSIS 评判模型法对四方金矿的采矿方法进行了优选；刘恒亮等［18］在综合博弈论和TOPSIS的基础上，建立了包括技术、经济、安全3 个方面采矿方法优选的综合评价指标体系，对某金矿破碎岩层下4种备选采矿方法进行了评价，最终确定了无底柱浅孔留矿嗣后充填法为该矿采矿方法优选方案。

上述方法各有特点和优势，但普遍存在计算繁琐、专业性强、多个采矿方案共用一组指标权重，这种处理方式忽视了指标在单一方案和整体方案中的重要程度，有失公平，会导致优选结果出现偏差。因此，重视指标权重在单一方案和整体方案中的作用，获取合理的指标权重是方案优选的关键。

为避免多个采矿方案共用一组指标权重导致优选结果出现偏差，由选取的评价指标构成完备事件组，将指标在单一方案和整体方案中的重要程度分别用先验概率和后验概率表示。先验概率与后验概率之间的关系可以用改进的贝叶斯公式进行描述，在定量分析的基础上，使每个采矿方法获取一组与之对应的指标客观权重。贝叶斯公式［19-21］作为一种数学方法，在进行多目标经济决策时属于客观赋权，克服了客观赋权计算繁琐的缺点，可操作性强，且获取的指标权重有合理的数学理论基础；反映了指标在单一方案和整体方案中的不同重要程度，体现了各方案的指标特点，使赋予的权重更加合理，优选结果更具有科学性。为寻求新的采矿方案数学优选方法，克服现有综合法指标权重处理中的不足，本研究根据采矿方案评价指标数据，基于贝叶斯公式建立采矿方法优选评价体系，进行采矿方法优选研究，以丰富采矿方案的数学优选方法。

1 基于贝叶斯公式建立优选模型

贝叶斯公式可表示为

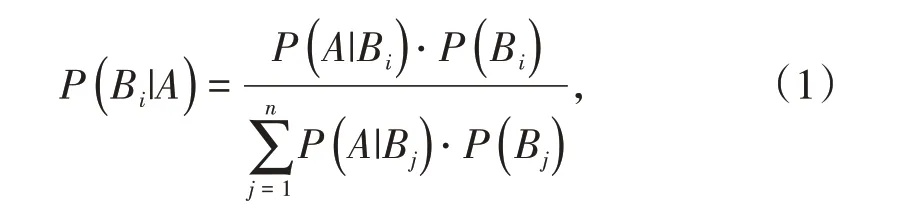
式中，n为事件B数量。

结合式（1）分析可知：事件A 发生的条件下事件B 发生的概率，与事件B 发生的条件下事件A 发生的概率不同，根据两者之间有确定关系的这个特点，用于描述采矿方案与评价指标之间的关系。若事件Ai表示待优选的采矿方案，Bij表示评价指标，待优选方案Ai发生的条件下事件Bij发生的概率（先验概率），与事件Bij发生的条件下事件Ai发生的概率（后验概率）不同，两者之间的关系可以用改进的贝叶斯公式优选模型进行描述。

1.1 基本定义

假设现有Ai( )i=1,2,3,…,m 个待优选采矿方案，每组评价方案有n个评价指标，第Ai个采矿方法的第j个指标可以表示为Bij( )i=1,2,3,…m;j=1,2,3,…,n。指标Bij之间的交集互为空集，评价指标Bi1,Bi2,Bi3,…,Bin组成全集，构成了完备事件组，且P( Ai)＞0，P( Bij)＞0。其中，P( Bij)是Bij的先验概率或边缘概率，因为它不考虑任何Ai方面的影响；P( Ai|Bij)是已知Bij发生后Ai的条件概率，也被称为后验概率；P( Bij|Ai)是已知Ai发生后Bij的条件概率，也被称为后验概率，即在方案Ai发生的条件下指标Bij的权重。

1.2 指标标准化

采矿方法评价指标主要有效益型、成本型、固定型、区间型。采矿方法技术经济指标属于非线性指标，主要分为成本型和效益型［22］，指标的关系及效益型指标与成本型指标之间的差异性问题可采用比重法进行指标标准化处理。假设aij表示第Ai种采矿方法的第Bij个未标准化的指标值，rij表示第Ai种采矿方法的第Bij个标准化后的指标值。当aij为效益型指标时，可采用下式进行指标标准化：

当aij为成本型指标时，可采用下式进行指标标准化：

标准化后的指标数据矩阵为

1.3 改进的贝叶斯公式模型与指标权重获取

（1）先验概率。由于某一方法Ai的指标Bij( j= 1,2,3,…,n )的概率P( Bij)为先验概率，不考虑其他任何方案的影响，只考虑指标Bij( j= 1,2,3,…,n)在某一方法Ai的所有指标（Bi1～Bin）中所占比重，因此，可以用均数法求出，体现了指标在单一方案中的重要程度。

（2）后验概率。第j 个指标条件下，有i 个采矿方法。P( Ai|Bij)表示某一方法Ai的指标Bij占所有方法（A1～Am）指标B1j～Bmj的权重，被称为后验概率，体现了指标在整体方案中的重要程度。

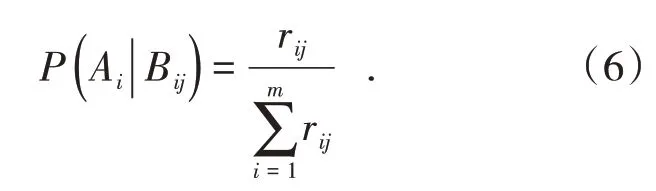
（3）指标权重。根据先验概率与后验概率的理论基础，将两者之间的关系利用改进的贝叶斯公式进行表述，方法Ai发生的条件下指标Bij的权重wij可表示为

式（7）的优点是每一方法都可以得到一组指标权重，即m组采矿方法可以得到m组指标权重，体现了指标在整体和部分中的关系与重要程度。

1.4 评价标准

方法Ai(i=1,2,3,…,m) 的指标标准化数据与权重运用简单线性加权法计算得到的指标综合评价值δi越大，对应的方法越优。δi可定义为

1.5 模型实现步骤

本研究基于贝叶斯公式建立的采矿方法优选模型的实现步骤为：①确定基本定义，先验概率、后验概率与改进的贝叶斯公式；②将待优选方法的指标进行标准化处理；③运用改进的贝叶斯公式获取指标权重，计算指标综合评价值，综合评价值越大则方案越优，综合评价值越小则方案越劣，从而确定采矿方法的优劣性。

2 实例分析

2.1 矿山概况

某铁矿矿区地势平坦，矿体赋存于地表2～6 m以下，矿体埋藏深度为+120 m～-240 m。地层岩性主要为区域变质岩，砂土层不存在砂土液化现象，地层分布稳定，力学特性良好。根据该铁矿所处地理位置、矿体赋存形态、开采技术条件、岩石力学特性等因素，适用的采矿方法有空场法和充填法。对采矿方法进行选择时，最初选用了大直径深孔落矿嗣后全尾砂充填的阶段矿房法（以下简称“方法1”）和机械化上向水平分层尾砂充填法（以下简称“方法2”），其技术经济指标如表1所示。

?

结合表1 分析可知：方法1 虽具有凿岩设备投资高、深孔凿岩技术要求高的不足，但该方法具有矿块生产能力大、劳动生产率高、采矿成本低等优点，适合地表不允许塌陷、矿体厚大、矿岩稳固的大中型矿山开采；方案2 不足在于矿块生产能力小、劳动生产率低、采矿成本高，同时该方法凿岩、出矿在采场内进行，安全性较差，但具有凿岩设备投资较少、钻孔技术要求低、采切工程量较少等优点。由于两种采矿方法在生产能力方面存在差异，因而导致其它指标不具备可比性，仅从两种采矿方法的优缺点也难以分辨优劣，故本研究采用改进的贝叶斯公式构建模型对采矿方法进行优选。

2.2 指标标准化与方案优选

2.2.1 指标标准化

如表1 所示，将该矿2 种采矿方法（方法1、方法2）分别记为Ai( i= 1,2)，选取的9 个评价指标分别记为Bij( i= 1,2;j=1,2,3,…,9)。其中效益型评价指标有采切工程量、矿块生产能力、采矿工效，成本型评价指标有采矿损失率、采矿贫化率、采切比、采矿设备费用、充填成本、采矿作业成本。

将效益型指标和成本型指标分别按式（2）和式 （3）进行标准化，标准化后的矩阵为

2.2.2 指标权重计算

对于待评价方法A1的指标B11的概率P( B11)，使用均数法公式（式（5））进行计算，计算过程为

同理，对于待评价方法A1、A2，指标B1j、B2j的概率P( B1j)、P( B2j)的计算结果如表2 所示。其中，P( B1j)表示指标在单一方法A1中的比重；P( B2j)表示指标在单一方法A2中的比重，反映了指标在单一方案中的重要程度。

?

在指标Bij( j= 1,2,3,…,9 )发生的条件下，概率P( A1|Bij)和P( A2|Bij)均采用式（6）计算。例如，在B11发生的条件下，A1发生的概率为P( A1|B11)=0.553 6，计算过程为

在B21发生的条件下，A2发生的概率为P( A2|B21)=0.446 4，计算过程为

同理，在Bij( j= 1,2,3,…,9 )发生的条件下，A1、A2发生的概率也可由式（6）计算，计算结果如表3所示。

?

根据式（7）计算Ai( i= 1,2 )发生的条件下指标Bij的权重，以在方法A1条件下指标B11的权重为例进行计算，计算过程为

同理，可计算出方法A1、A2条件下，指标Bij( j= 1,2,3,…,9 )的权重如表4 所示。由表4 可知：方法A1、A2各自得到一组指标权重，反映了指标在单一方案和整体方案中的不同重要程度。

?

2.2.3 方案优选

根据式（8），可通过简单线性加权法，计算出方法1的指标综合评价值δ1=0.830 7，计算过程为

同理，可得到δ2=0.723 8。由此可知，方法1、方法2 的指标综合评价值分别为0.830 7、0.723 8。因此，基于贝叶斯公式建立的既兼顾效益又兼顾成本的采矿方法评价体系中，实例矿山适宜使用大直径深孔落矿嗣后全尾砂充填的阶段矿房法开采。

2.3 优选结果现场应用效果

在矿山实践中，方法1 取得了较好的应用效果。采矿方法试验期间，矿山取得的技术经济指标如表5所示。

由表5可知：矿山实际生产能力达到了1 180 t/d，除了贫化率高出设计指标2.65 个百分点外，其它技术经济指标均优于设计指标，表明基于贝叶斯公式构建的采矿方法优选模型具有一定的适用性。

?

3 结 论

（1）通过建立采矿方法优选效益型和成本型指标体系，基于贝叶斯公式建立了采矿方法优选模型，并运用到某铁矿采矿方法优选实践中，得出了适宜该矿山开采使用的采矿方法。

（2）为避免常用采矿方案数学优选方法采用同一权重给项目评价带来的不公平性，基于贝叶斯公式建立了评价模型，指标评价体系中计算每一指标的权重，使每组采矿方案得到一组与之对应的指标权重，使得权重赋予更加合理、科学。

（3）以某矿山为实例，综合考虑各种技术经济指标，运用贝叶斯公式确定的最优采矿方法为大直径深孔落矿嗣后全尾砂充填的阶段矿房法。矿山开采初期采矿方法试验结果表明，基于贝叶斯公式构建的采矿方法优选模型有一定的实用价值，为采矿方法优选提供了新思路。