基于移动阵列电极的盾构超前探测正演响应分析
赵栓峰,拜云瑞,黄 涛,魏明乐
(西安科技大学机械工程学院,陕西 西安 710054)
隧道掘进机(Tunnel Boring Machine,简称TBM)近年来已成为隧道开挖领域必不可少的机械工具,而其施工过程的超前探测也是目前隧道开挖的热点、难点问题。目前,盾构超前探测常通过声波、直流电等方法对TBM 前方的地质情况进行探测、分析解释以及预报,保证隧道开挖的安全[1]。
其中,研究较为广泛且最为成熟的是直流电阻率法。众多学者专家通过电极排布[2]、影响因素[3]、理论分析[4]、正演模型[5]、反演算法[6]等方面对直流电阻率法加以研究,推动了直流电阻率法超前探测的发展。但受TBM 隧道施工空间的限制,传统直流电阻率法只能在掌子面后端布置测线实施测量,使得掌子面后端响应较为灵敏,而掌子面前端有效数据则会因干扰而丢失。为解决此类问题,德国GET勘探技术公司研制了一款隧道钻孔电气超前探测系统(Bore-Tunneling Electrical Ahead Monitoring,简称BEAM)[7-10],其原理主要是将电流通入接地电极,测量其余电极的电压,通过百分比频率效应及电阻率来进行水文地质分类评估。BEAM 系统探测灵敏度高,装置的稳定性好,并且可以实现实时在线探测,但其未利用层析成像,只能依靠结果定性分析前方地质环境,无法定量描述,使得BEAM 系统在分辨率、位置精度、观测距离等方面无法给出较为精确的结果。
因此,为提高探测效果、直观且定量地分析掌子面前端地质情况,结合直流电阻率成像方法及BEAM 系统硬件的优点,研究适用于成像系统的移动阵列电极盾构超前探测方法,采用有限元数值模拟方法分析不同异常反应下的响应情况,并验证适用于成像系统的移动阵列电极盾构超前探测方法的可行性。
1 移动阵列电极盾构超前探测系统组成
移动阵列电极盾构超前探测系统在TBM 施工环境基础上加以改进,将其阵列电极、数据采集、图像重建3 个单元布置在TBM 上,其布置如图1所示。阵列电极按用途分为测量、接地及保护三类电极。其中,测量电极由刀盘上一排刀头充当,测量时,按顺序通电或测量;接地电极为后方墙内锚杆;对TBM 护盾通入电流用作保护电极。为保证数据自动采集及显示过程不被干扰,将数据采集和图像重建两个单元与TBM 系统连接后放入主控室内。
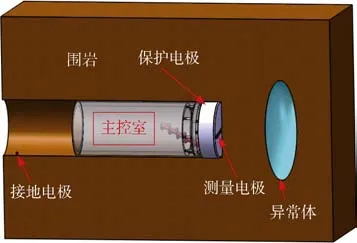
图1 移动阵列电极盾构超前探测系统的布置Fig.1 The arrangement of advance detection system of moving array electrode for shield tunneling
2 有限元仿真分析
2.1 聚焦点电源电场的边界条件及变分处理
为提高电源点周围的计算精度,本文通过异常点位法求解聚焦点电源电场[11-12]。
假设电导率为σm的均匀介质中存在电流为I的点电源A,大地的电导率为σ0,其内部异常体的电导率为σ,且σ′=σ–σ0。δ(A)用来表示在全空间以A为中心的狄拉克函数。
在聚焦点电源电场中,总电位ν是正常电位值u0与异常电位值u之和,则总电位ν的微分方程可化作:
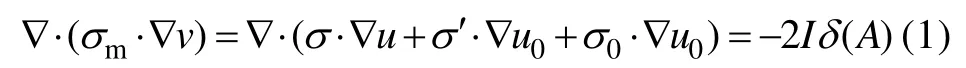
若令∇·(σ0·∇u0)=-2Iδ(A),则u的微分方程为:
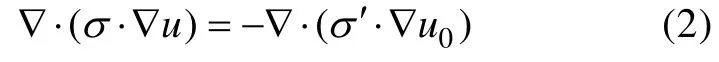
u的边界条件为:
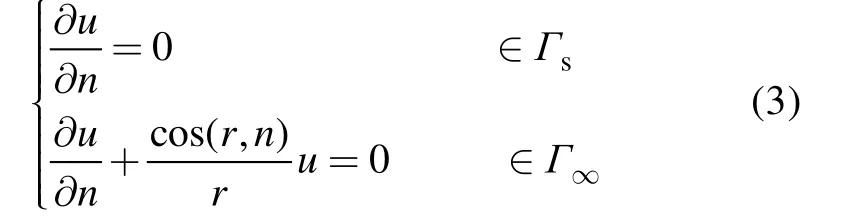
式中r为从点电源到测量点A间的距离;Γ为在空间任意闭合面;Γs是地面边界;Γ∞是无穷远边界;n为边界外法线方向。
在运用有限元法求解聚焦点源电场时,把边值问题转化为与之对应的泛函式[13],即变分处理。将上述边界问题变分处理得:
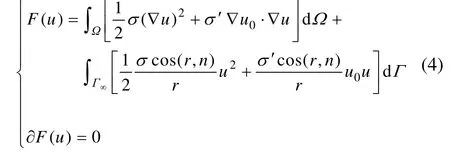
2.2 有限元网格划分
有限元网格划分过程主要有以下3 个步骤[14-15]:设置网格单元属性;设置网格划分选项;生成网格。本文进行二维电场仿真,在整个求解区域选择不重叠三角形为实体模型单元。在划分网格时,需要通过电位变化率来考虑、调整网格密度,一般情况下,变化率较大处需要密集化网格提高精度,变化不明显处则可疏化网格加快速度。本模型采用的是自适应网格剖分方法,自适应网格剖分法可在需要密集网格处自动提高网格质量[16]。
2.3 单元分析与总体合成
在变分处理中的泛函,需对求解域上做积分处理,可根据各单元积分分量和求得:
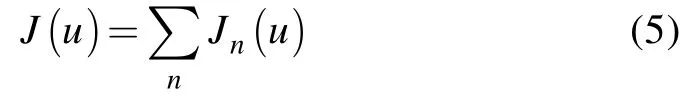
单元内部电导率为常量,则泛函为:
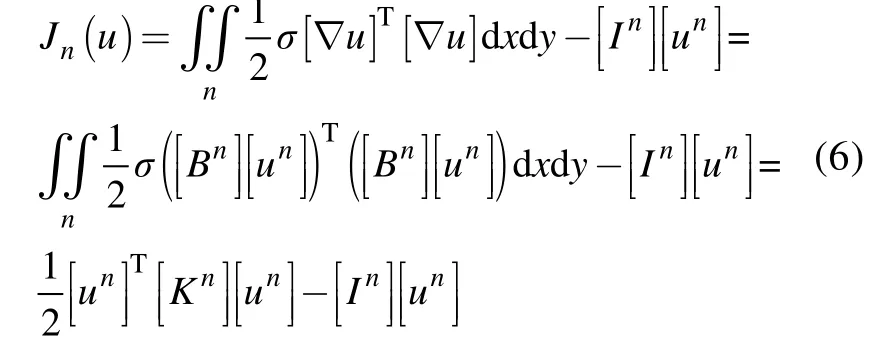
按式(5)对所有单元泛函相加,并将式(6)代入,得出整个求解区泛函,得到的即为被离散化为多元二次函数的泛函J(u):
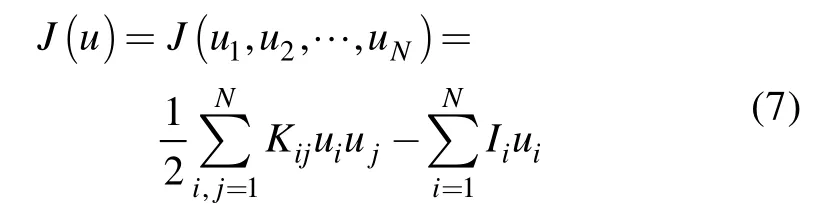
因此,变分问题式(4)可转化为二次函数极值问题,由极值条件得,函数对于各变量导数为零:
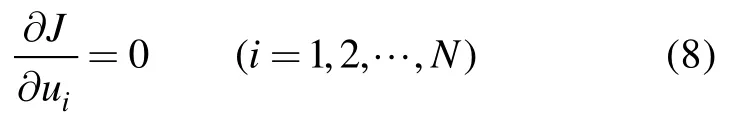
将式(7)代入式(8)可得:
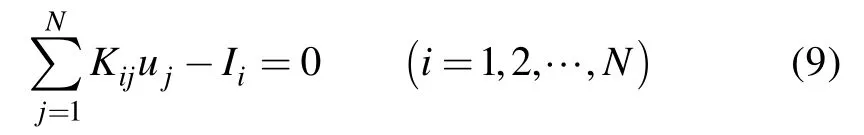
将式(9)以矩阵的形式表示为:

其中,[K]为方程组的系数,即刚度矩阵,其值由节点坐标及电导率分布决定且在各求解模型中已知;式(10)右端场源列矢量为已知量,因此,求解式(10)便可求得整个求解域内电位值。
2.4 地电几何实体模型的建立与仿真实验
利用Comsol Multiphysics 建立地电几何实体模型,模型如图2 所示。将所研究区域地电模型建立为长80 cm×宽40 cm 长方形,内部视作未开挖围岩层,电阻率设置为20 Ω·m。在其中部左侧开挖出一条长40 cm,直径10 cm 的隧道。在隧道开挖过程中,TBM 通常紧贴在隧道前端且不作为研究对象,因此,可等效为电极布置在隧道内壁。而根据模型几何缩放比例,可将电极视作为点电极,从而能更加精准测量对应处电位。测量电极共12 个,均匀布置在隧道最前端掌子面上,各电极间距为0.8 cm,图2 中由上到下依次为1 至12 号。保护电极被简化为TBM 护盾所贴内壁的上下各5 个电极,其所在截面半径5 cm。根据测算,模型宽度为40 cm,满足大于保护电极截面半径5 cm 的6倍以上,此时可将四周外部面看做无穷远处,电位视为零。
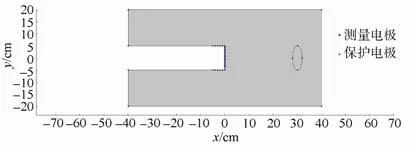
图2 地电几何实体模型Fig.2 Geometrical solid model of geoelectricity
仿真测量时,首先给1 号电极施加激励电流,分别按顺序测量2—12 号测量电极的电压,然后依序换下一个测量电极作为激励电极进行供电,按顺序测量余下测量电极的电压,至此类推至12 个电极全部作为激励电极并将测量电极全部按序测量完成。整个仿真实验过程中,异常体的大小、形状、位置等变量可根据需要调整,电极布置及测量方式维持不变。
3 正演仿真结果分析
3.1 保护电极是否存在时的正演响应
当不存在保护电极时,给7 号电极通入1 mA的直流电作为激励电极,其电压分布图如图3a 所示;当存在保护电极时,给7 号电极与保护电极同时通入1 mA 的直流电,其电压分布图如图3b 所示。
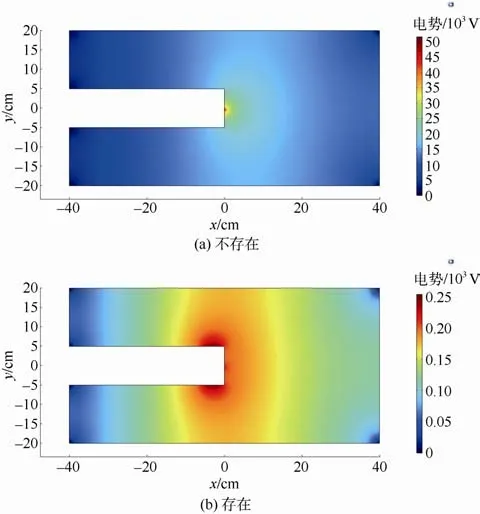
图3 保护电极是否存在的电压分布Fig.3 Voltage distribution diagram for presence or absence of protective electrode
通过对图3 进行比较可发现,当不存在保护电极时(图3a),电场在传播的过程中衰减较为迅速,对电极施加激励可产生一个长轴15 cm、短轴10 cm的椭球形分布电场,其电场范围所产生的探测距离仅与隧道同宽,无法完成探测要求。而存在保护电极时(图3b),其电场范围前向传播至40 cm 处仍未衰减至0 V,这是由于保护电极通入与激励电极同极性的电流,致使激励电流出现“同极相斥”的现象进而产生聚焦,使测量范围覆盖近乎整个模型,大大增强了探测范围。
3.2 异常体尺寸变化时的正演响应
设置异常体形状为正方形,电阻率值ρ=0.05 Ω·m,使其中心对准y=0 cm 处(即隧道几何中心轴线处)且距隧道掌子面D=20 cm。分别以异常体边长L=10 cm、L=15 cm 和L=20 cm 三种情况作为对照组,向激励电极及保护电极同时通入1 mA 的直流电,并按既定测量方式完成仿真分析。
通过仿真测量得到异常体尺寸变化时测量电极电压关系如图4 所示。从图4 可以得到,异常体尺寸的变化会导致测量电极电压分布随之变化。当改变异常体的尺寸大小使边长L增大时,由于其电阻率较低产生低阻态效应,使得周围围岩电阻率的影响范围增大,从而相同电极上电压值会降低。
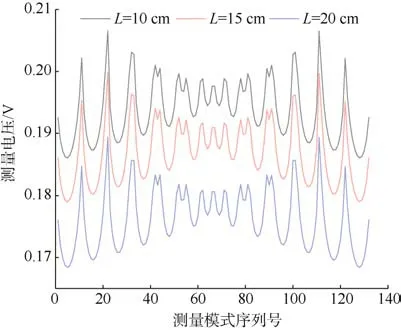
图4 异常体尺寸变化时各测量电极的电压Fig.4 Potential electrode voltage of different abnormal body size
3.3 异常体形状变化时的正演响应
设置异常体电阻率值ρ=0.05 Ω·m,使其中心对准y=0 cm 处(即隧道几何中心轴线处)且距隧道掌子面D=20 cm。分异常体形状为边长L=10 cm 的正方形、长20 cm×宽5 cm 的矩形和R=5 cm 的圆形3 种情况作为对照组,向激励电极及保护电极同时通入1 mA 的直流电,并按既定测量方式完成仿真分析。
通过仿真测量得到异常体形状变化时测量电极电压关系如图5。从图5 可以得到,当异常体形状为矩形、圆形、正方形时,电极电压依次递减。这是由于在3 种异常体形状所设置的中心点位置相同的情况下,其测量电极与各自作用面间距离不同,从而导致测量电压不同。

图5 异常体形状变化时各测量电极的电压Fig.5 Potential electrode voltage of different abnormal body shape
3.4 异常体位置变化时的正演响应
将异常体位置变化分解为纵向偏移和横向偏移两个问题。先对纵向偏移问题进行分析,即异常体与掌子面距离保持一定,但在纵向方向上进行上下偏移。设置异常体形状为长半轴A=5 cm、短半轴B=2 cm 的椭圆,电阻率值ρ=0.05 Ω·m,使其中心距隧道掌子面D=20 cm。异常体椭圆短轴处于y=5 cm(向上偏移5 cm)、y=0 cm(不发生偏移)、y=-5 cm (向下偏移5 cm)3 种情况作为对照组,向激励电极及保护电极同时通入1 mA 的直流电,并按既定测量方式完成仿真分析。
通过仿真测量得到异常体中心点偏离隧道中轴线不同距离时测量电极电压关系(图6)。从图6 可以分析得到,当异常体短轴处于y=0 cm 时,相同电极上电压值最大而纵向的偏移会导致电压值减小。并且由于异常体短轴处于y=5 cm 时其边界外法向量与测量电极间夹角小于异常体短轴处于y=-5 cm 时其边界外法向量与测量电极间夹角,通过式(4)得到,异常体短轴处于y=5 cm 时其测量电压大于异常体短轴处于y=-5 cm 时的测量电压。
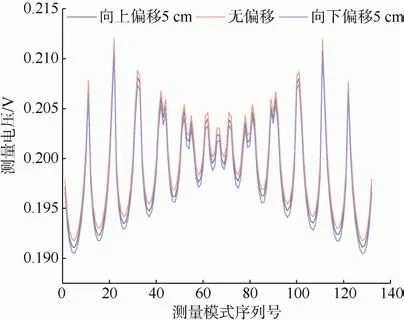
图6 异常体的中心点偏离隧道中轴线不同距离时各测量电极的电压Fig.6 Voltage of measurement electrodes at differeat distance of geometric center of abnormal body to the central axis of tunnel
第二类问题是横向偏移问题,即当异常体中心恒对准y=0 cm 处,而与掌子面的距离发生变化。设置异常体形状为长半轴A=5 cm、短半轴B=2 cm 的椭圆,电阻率值ρ=0.05 Ω·m,使其中心对准y=0 cm处(即隧道几何中心轴线处)。异常体中心距隧道掌子面D=10 cm、D=20 cm 和D=30 cm 三种情况作为对照组,向激励电极及保护电极同时通入1 mA 的直流电,并按既定测量方式完成仿真分析。
通过仿真测量得到异常体中心点到掌子面距离不同时测量电极电压关系(图7)。从图7 可以分析得到,在相同电极的情况下,随着异常体中心距隧道掌子面距离增大,电极上电压降低。分析式(4)可得,在点电源电场求解异常点电位的过程中,距点源电场距离越远,异常点的电位值越小。
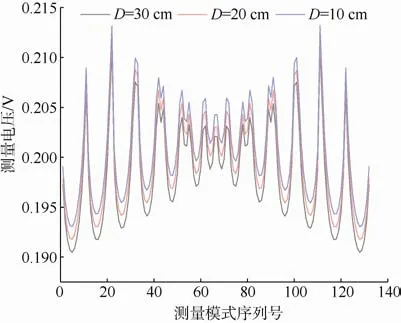
图7 异常体的中心点到掌子面的距离不同时各测量电极的电压Fig.7 Voltage of different measurement electrodes at different distance of the center of abnormal body to working face
4 移动阵列电极的盾构超前探测实验
4.1 基于相似性原理的物理模型实验平台设计
物理模型实验装置见图8。实验台的外壳尺寸为长80 cm×宽40 cm×高50 cm,由厚度为0.8 cm的亚克力板制成。选择一个椭圆柱形黄铜作为低阻异常体,其长轴为10 cm,短轴为4 cm,厚度为2 cm,电阻率值为0.05 Ω·m。为便于改变异常体的位置,在实验台上方装有可沿XYZ三方向自由度平动的丝杠螺母机构。为了使电极与介质充分地接触,减小接触电阻的影响,将水注入实验台至40 cm 处作为模拟围岩,其电阻率值为20 Ω·m。选用外径10 cm,内径9 cm,长为40 cm 的PVC 空心圆管模拟盾构机,将导电铜箔纸贴在圆管外壁上模拟护盾并将电极均匀固定在护盾周围用作保护电极。模拟刀盘选用直径为10 cm 圆形亚克力板,在其上直径方向均匀布置12 个间距为0.8 cm 的铜制螺栓用作12 个测量电极,将电极连接导线装入有防水密封轴承的轴内,轴的另一端连接联轴器与步进电机用于刀盘旋转。盾构超前探测实验系统由开关电源、恒流源激励模块、多路转换器、主控器、信号处理与采集模块,计算机组成。开关电源用以给恒流源激励模块及步进电机系统供直流电,电流进入恒流源激励模块放大后产生50 μA~10 mA 的恒定电流,通过多路转换器(CD4067)的选择依次通入激励电极内。信号处理与采集模块也与多路转换器相连,通过多路转换器的选通依次对测量电极电压进行测量和采集。主控器(MSP430F149)负责对多组多路开关选择通断,用以按次序控制激励及测量,最终将数据传入计算机中进行成像。

图8 盾构超前探测物理模型实验装置图Fig.8 Physical model experiment device picture for advanced detection of shield
4.2 实 验
实验时,按要求连接电路,测量方式与仿真实验过程相似,从一端起,将激励通入单个测量电极,按顺序测量余下测量电极的电压值,并通过采集模块传入计算机存储,再按次序将激励转换至下一个测量电极,直至12 个电极全部被激励且测量完毕,则完成一次测量。样本可以通过改变不同异常体的形态与位置得到。
4.3 实验结果及分析
在完成对实验各测量电极电压值的采集后,绘制测量电极—测量电压图像,选取仿真与实验模型中,异常体中心对准y=0 cm 处(即隧道几何中心轴线处)且距隧道掌子面D=15 cm 的一组进行对比,图像如图9 所示。在对比物理实验所得结果曲线与仿真结果曲线可得其变化趋势基本一致,通过测算,仿真所得实验结果与物理模型实验结果间的平均相对误差为0.7%,在一定程度上验证了基于移动阵列电极的盾构超前探测方法的可行性。
5 结论
a.对保护电极是否存在的情况作了对比,通过电压、电流分布可知,保护电极的存在能使电场较好地向前传播,从而增大探测范围。因此,有必要添加保护电极。
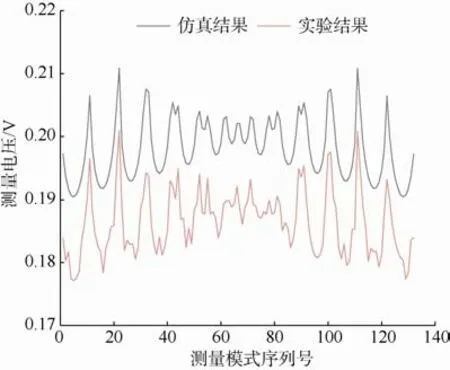
图9 仿真结果和实验结果Fig.9 Simulation results and experimental results
b.对异常体不同尺寸、形状、位置、分别作了对比,据其电压分布显示,同一测量电极的电压值随着异常体尺寸的增大而变小;几何中心位置相同的矩形、正方形和圆形异常体,矩形异常体的测量电压最大,正方形异常体得测量电压最小;当异常体向上偏移时电极的电压要比异常体向下偏移时电极的电压大一些,且异常体距隧道掌子面距离越远,各测量电极电压越小。因此,采用移动阵列电极的盾构超前探测对异常体尺寸、形状、位置变化响应能够做出规律性响应。
c.通过相似性原理建立了移动阵列电极的盾构超前探测的物理模型实验平台,最终得出电极间仿真实验结果与物理模型实验结果之间的平均相对误差为0.7%,在一定程度上验证了基于移动阵列电极的盾构超前探测方法的可行性,为后续应用提供了理论保障。

