煤复电阻率频散机理研究
郭跃辉,张玉贵,2,李 健,周 猛
(1.河南理工大学安全科学与工程学院,河南 焦作 454000;2.中原经济区煤层(页岩)气河南省协同创新中心,河南 焦作 454000)
近年来,频率域复电阻率测井(Complex Resistivity Logging,简称CRL)已经在岩石上广泛应用。该方法可以实现在频率域和空间域的高密度测量,较其他物探方法具有获取电性参数多,且多参数对比解释可提供更丰富的煤体激电地球物理响应特征,在深部构造、固体矿产、油气资源、水文地质、工程地质、环境监测等领域发挥着重要的作用。然而,这种技术在煤矿测井中应用却很少。煤的频散机理是复电阻率测井技术的理论基础,不同的频率范围,煤的频散机理(包括激发极化、电磁感应、介电极化)和所研究的电场性质各不相同,因此,明确煤的频散机理,对复电阻率测井在煤矿上的应用具有重要的意义。
在岩石上,国内外许多研究学者表明,岩石的复电阻率频散机理与岩石的激发极化现象有关[1-4]。向葵等[5]进行了不同矿化度下页岩的复电阻率实验研究,运用激发极化模型进行反演,结果表明:电阻率随着矿化度的增大而减小,极化率整体上逐渐减小,最后趋于稳定。童茂松等[6]首次利用奇异值分解的算法从激发极化角度解释了弛豫时间,将界面极化频率与激发极化建立了联系,这为激发极化与岩石复电阻率频散现象的研究奠定了基础。孙斌等[7]利用AutoLab-1000 高温高压岩心测量系统,对影响激发极化的因素(矿化度、温度、压力)进行了研究,得出矿化度变化对于泥质砂岩复电阻率的振幅、相位、实部、虚部有不同的影响;在储层条件下,对泥质砂岩的频散特性进行了分析研究,得出储层深度增加会导致泥质砂岩的电阻率、频散程度降低。
关于煤复电性的研究成果很多,主要采用单频、双频、多频的交流电测量[8-12]。王云刚等[13]在1 MHz和160 MHz 测试频率下,对不同变质程度的原煤样及湿煤样进行了复电阻率测试,得出1 MHz 下原煤样与湿煤样的差异要比160 MHz 频点下原煤样与湿煤样的差异大。郭晓洁等[14]采用日置3533-50LCR测试仪进行了扫频模式下100 Hz~100 kHz 连续频率下复电性研究,测量了常温常压下煤体复电性特征,分析煤体结构与阻抗振幅之间的关系,通过将所测得的阻抗振幅值分别与煤体各个物性参数进行拟合,找出预测煤体基础性质的优势频段。柳苏等[15]在0~100 kHz 范围内测量了4 种变质程度煤样的复阻抗幅频相频曲线,发现在相同电性频率域下不同变质程度的煤样所表现出来的阻抗及相位不同,并满足激发极化机理。
目前,对于煤的复电阻率,前人主要研究了煤复电阻率的各向异性和幅频相频曲线的变化规律。而对于煤复电阻率频散的物理机理有待进一步研究。煤是一种固态的可燃有机岩,具有和岩石相似的频散现象。为了研究煤复电阻率的频散机理,笔者运用双电层形变假说,将煤复电阻率频散数据进行从频域到时域的傅里叶逆变换,并和岩石频散数据对比,而后将Cole-Cole 模型与实验数据拟合,初步明确了在小于200 kHz 时,煤复电阻率的频散特性主要受激发极化影响,电磁感应的影响很小。
1 样品制备与实验
1.1 样品制备
在焦作矿区赵固、九里山煤矿二1煤层采样,样品沿平行层理,加工成尺寸为Φ50 mm×100 mm的圆柱体,如图1 所示。

图1 焦作矿区赵固矿与九里山矿样品Fig.1 Samples from Zhaogu Mine and Jiulishan Mine in Jiaozuo mining area
1.2 实验系统与方案
1.2.1 实验系统
实验系统为复电阻率测试系统,如图2 所示,包括IM3533-01 型LCR 阻抗测量仪、带黏合剂的导电铜纸(导电的黏合剂与样品接触面干燥,不发生极化现象)及固定装置。
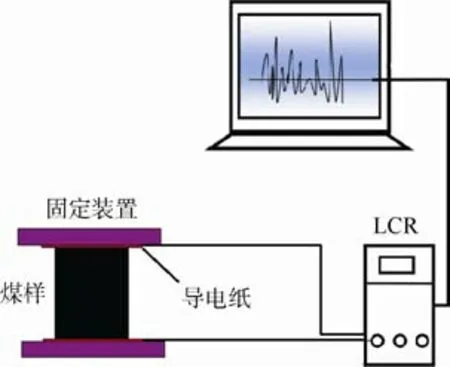
图2 复电阻率测试系统Fig.2 Test system for complex resistivity
1.2.2 实验方案
实验开始前将样品浸泡在水中一段时间,使其孔隙的含水程度接近于天然条件;而后在样品轴向两端贴上导电铜纸,控制电流大小不变,只在频率为0~200 kHz 内采用两电极法;利用IM3533-01 型LCR 阻抗测量仪,测量含水样品的复阻抗幅值和相位,然后换算成复电阻率的幅值相位(其中相位以绝对值表示)。同时采集一组含水的砂岩数据进行对比分析。
1.3 样品复电阻率测量
1.3.1 频率域
图3 为赵固、九里山平行层理含水样品的复电阻率幅频相频曲线,图4 是用于和样品结果作对比所测的含水砂岩复电阻率幅频相频曲线。从图3 可以看出,在电流频率为0~200 kHz 期间,焦作赵固矿和九里山矿样品复电阻率幅值随频率增加而减小,复电阻率相位随频率的增大先增大后减小。

图3 赵固和九里山含水样品平行层理的复电阻率幅频相频曲线Fig.3 Amplitude-frequency and phase-frequency curves of complex resistivity of parallel bedding in different areas
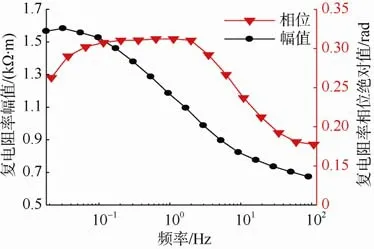
图4 含水砂岩的复电阻率幅频相频曲线Fig.4 Amplitude-frequency and phase-frequency curves of complex resistivity of water-bearing sandstone
1.3.2 时间域
傅里叶变换理论表明,任何时间函数f(t),只要满足傅里叶积分定理的条件,就可以通过积分变换转变为频率域的函数F(ω)。反过来,频率域的函数F(ω)通过傅里叶逆变换又可转变为时间域的函数f(t)[16]。所以,时间域曲线图可以通过傅里叶逆变换得到。样品电压的充电曲线数据是通过测得的复阻抗的频散数据乘以电流得到电压的频散数据,然后将电压的频散数据通过傅里叶逆变换得到的。图5为赵固、九里山含水样品平行层理的电压充电曲线,图6 为含水砂岩的时间域激发极化充电曲线。从图5 可以看出,焦作赵固矿和九里山矿样品电压充电曲线具有明显的一次场和二次场。
2 样品复电阻率频散机理
2.1 样品导电机理
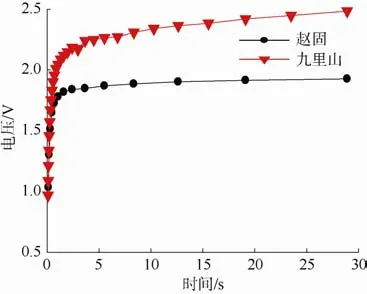
图5 赵固和九里山含水样品平行层理的电压充电曲线Fig.5 Voltage charging curve of water-bearing samples with parallel bedding from Zhaogu and Jiulishan
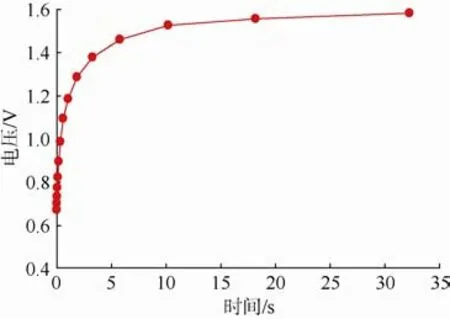
图6 含水砂岩的时间域激发极化充电曲线Fig.6 Charging curve of time domain induced polarization of water-bearing sandstone
在交变电磁场中存在两种电流,即传导电流和位移电流。前者由带电粒子(电子、离子等)的定向运动(电磁感应、激发极化)所引起,后者由极化分子定向排列(介电极化)所引起[17]。在导电介质中,总电流密度j为:
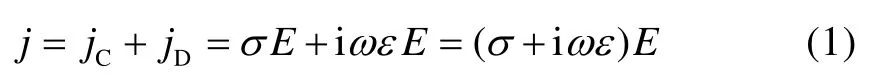
式中jC和jD分别是传导电流密度和位移电流密度,A/m2;E是电场强度,V/m;σ是电介质的电导率,s/m。ε是电介质的介电常数,F/m;ω是角频率,rad/s。
式(1)表明,当同时存在传导电流和位移电流时,联系电流密度和电场强度关系、表征介质导电特性的电导率为复数,且随频率的变化而变化。通常称此为“复电导率的频散特性”。
复介电常数ε在0~200 kHz 频段上随频率变化很小,ε/ε0<15[18],其中,真空介电常数ε0=8.854×10–12F/m。经计算可知(读取图3a 中幅值):在0~200 kHz 频率范围内ωε/σ随电流频率增大而增大,在200 kHz 时,取得最大值ωε/σ=0.068 8。由此可知,在0~200 kHz 频段上,激发极化和电磁感应起作用,与介电极化相关的位移电流可以忽略,这与文献[17]的相关结论一致。
2.2 样品激发极化机理
石墨是电导体,电阻率在10–8~10–2Ω·m,激发极化频段在0~100 Hz[19]。由图3 可知,煤样的电阻率远大于石墨的电阻率,激发极化频段比石墨要大得多,符合离子导体的激发极化。从图5、图6 可以看到样品与砂岩具有相似的充电曲线。另外,图 3 样品复电阻率的相位是负值(图中相位已做绝对值表示),这说明样品在电路中呈容性,满足离子导体的双电层形变假说的条件,因此,本文采用离子导体的双电层形变假说来解释煤的激发极化现象。
激发极化是发生在地质介质中,因外电流激发而引起介质内部出现电荷分离,产生一个附加的过电位的一种物理化学现象。这种现象反映了外电流引起的地下介质中电荷的分化和转移。在时间域,当向样品中通入恒定电流时,从图5 中可以看到在样品两端有一个瞬间的一次场ΔU1存在,同时在电场力的作用下溶液中的离子发生定向运动,在双电层的两端堆积(相当于电容的充电),形成二次场ΔU2(t),随着时间的推移双电层充电完全,二次场ΔU2(t)达到最大值。一次场ΔU1和二次场ΔU2(t)叠加形成总场ΔU(t)[15,20]。
在频率域,在一个周期内电流的方向要改变一次。在低频时,一个周期的时间较长,双电层能够完全充电,二次场ΔU2(t)能够达到最大值,样品能够完全极化。但是,随着频率的增大双电层充电不完全,二次场ΔU2(t)达不到最大值,样品不能够完全极化,也就是说,总场电压ΔU(t)随着频率的增大而减小。而通入的是恒定的交变电流,电流大小不变,总场电压ΔU(t)在减小,也就是复阻抗的幅值随着频率的增大而减少的,即复电阻率的幅值随着频率的增加而减小。从图3 中也能够看到复电阻率的幅值随着频率的增大而减小。另外,在电流频率f→0,时即为直流,不存在相位的变化,即复电阻率相位φ=0。在电流频率f→∞时,样品来不及发生激发极化,即复电阻率相位φ=0[19]。从图3 可以看到:在测量频率范围(0~200 kHz)样品复电阻率相位随着电流频率增大先增大后减小;以1 kHz 为界点分成两个区域,在低频区域;样品复电阻率的相位随频率增大而增大,在高频区域,样品复电阻率相位随着频率增大而减小。可以看到,当f→0,f→∞时,复电阻率的相位φ→0。在所做的实验中,极值点大致都出现在100 Hz~10 kHz 这个频段上。
2.3 Cole-Cole 模型
Cole-Cole 模型是建立在激发极化基础之上的复电阻率频散模型,用此模型对实验数据进行拟合,来验证样品在0~200 kHz 这个频段上发生的是否为激发极化现象。另外,除了激发极化效应外,电磁感应效应的低频部分也可用Cole-Cole 模型描述[17]。所以,当同时存在激发极化效应和电磁效应时,实测的复电阻率频散特性可表示成单个或多个Cole-Cole 模型之和或之积。本次采用单Cole-Cole 模型对所测数据进行拟合。
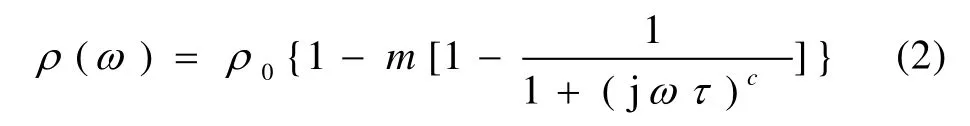
式中ρ(ω)是角频率为ω时的复电阻率,Ω·m;ρ0是频率为零时的电阻率,Ω·m;m、c分别是激发极化的极化率和频率相关系数,无量纲;τ为时间常数,s。
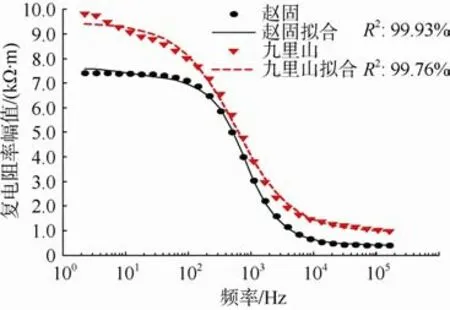
图7 赵固和九里山含水样品平行层理的复电阻率幅值Cole-Cole 模型拟合曲线Fig.7 Amplitude fitting curves of Cole-Cole model of complex resistivity of different samples with parallel bedding
从图7 中可以看出,在0~200 kHz 频率范围内,用来表征激发极化和电磁效应的Cole-Cole 模型对样品频散的实验数据拟合得非常好。另外,在图3中相位为负值(图中已做绝对值处理),表明样品对外呈现容性,这就说明低频时,样品复电阻率的频散特性主要是由激发极化效应引起的。如果样品复电阻率频散特性为电磁感应起主要作用,那么样品电性总体应该呈现感性,复电阻率相位应为正值,因此,煤复电阻率频散主要受激发极化影响,电磁感应影响很小。
由此看来,在利用复电阻率测井评价煤层时,当频率小于200 kHz 时,其测井理论应当建立在激发极化效应基础之上,在交变电场的作用下,难免有不同程度的电磁感应效应的干扰,一般随着频率的增加,电磁效应会逐渐增强,这种效应也能引起电场随频率的变化,并且在低频段激发极化和电磁感应一样满足Cole-Cole 模型。另外,笔者做了导电纸、薄铜板、厚铜板、金属煤样罐复电阻率的对比实验,发现导电纸相对其他极板来说电磁感应影响最小。受仪器的限制,测不到200 kHz 以外复电阻率的电频散数据,从图3 复电阻率相位的趋势来看200 kHz 以外还有激发极化现象。
3 结论
a.电流频率在0~200 kHz 时,所测得的焦作赵固矿和九里山矿样品复电阻率具有频散特性,并与岩石相似,复电阻率幅值随频率增大而有规律的减小,复电阻率相位绝对值随频率的增大先增大后减小。引起样品复电阻率频散特征的原因主要是激发极化现象,电磁感应的影响很小。
b.焦作赵固矿和九里山矿样品复电阻率幅值与Cole-Cole 模型相关性很好,R2能够达到99%,说明该样品复电阻率频散特征符合双电层形变假说理论。
c.通过与石墨(属于电导体)的复电阻率频散数据对比,得出煤电阻率远大于石墨的电阻率,煤的激发极化频段更宽。
d.煤复电阻率测量和频散机理的研究成果为复电阻率测井提供了理论依据,能够用于指导复电阻率测井。

