导管架平台健康监测中的信号处理技术

高喜峰，徐增伟，徐万海

（天津大学 水利工程仿真与安全国家重点实验室，天津 300072）

导管架平台是海洋油气资源开发的关键装备，因其工作环境复杂恶劣，可能遭受到意外打击，且受到海水和生物腐蚀的影响，极易发生损伤[1]。导管架平台健康监测是进行平台特征提取和损伤识别的有效手段。通过在结构的关键部位埋设或安装传感器，可获取结构振动信号，提取反映结构健康的特征信息，评估分析结构的安全性，对危及结构安全的状态及时预警，从而避免重大事故的发生，保证导管架平台的服役安全[2]。

传感器捕获的信号包含了反映结构健康的特征信息，如何从信号中提取这些信息，是导管架平台健康监测的重要内容，需要可靠的信号处理方法的支持[3]。通过提取信号特征，能够判定结构是否发生损伤以及损伤的程度，实现损伤检验和结构健康监测的目的，这对于保障导管架平台和作业人员安全，延长平台使用寿命具有重要意义。

在振动信号分析和处理中，常用的方法包括：傅里叶变换（Fourier Transform）、小波变换、Wigner-Ville分布和希尔伯特-黄（Hilbert-Huang）变换[4]。傅里叶变换可以用于研究信号的频域特征，适用于处理平稳信号；小波变换、Wigner-Ville 分布和希尔伯特-黄变换可以研究信号的时频分布，在处理非平稳信号方面具有很好的效果。由于Wigner-Ville 分布在分析多分量信号时存在严重的交叉项干扰，在导管架平台健康监测与特征提取中的应用较少，因此本文将对除Wigner-Ville 分布外的3 种方法的发展、理论、优缺点以及在导管架平台健康监测中的应用情况进行系统的总结与讨论，以期为后续导管架平台健康监测和振动特征提取的发展提供参考和启发。

1 基本理论

1.1 傅里叶变换

傅里叶变换（Fourier Transform，FT）是振动信号处理和分析中最基本、最经典的方法，由J.B.J 傅里叶提出[4]。其原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加[5]。

对于信号x(t)，其傅里叶变换是将信号从时域转化到频域的过程，定义为：

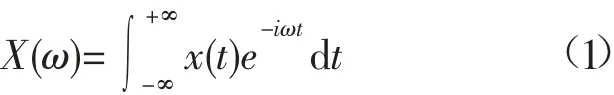
式中：X(ω)表示信号x(t)的傅里叶变换；t表示时间；ω 表示信号的频率。

1946 年，Gabor 引入“窗口”的概念，提出了短时傅里叶变换（Short Time Fourier Transform， STFT），也称为加窗傅里叶变换[6]，定义为：

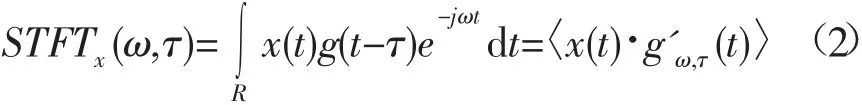
1.2 小波变换

小波变换（Wavelet Transform，WT）是对短时傅里叶变换的延续和发展，可在时域和频域提供精确的定位能力[7]，被誉为“分析信号的显微镜”。小波变换的概念是由Morlet 于1984 年在进行人工地震勘探信号分析中正式提出的。此后，Meyer 提出正交小波基的概念，并出版了《小波与算子》一书，成为了小波理论诞生的标志[8]。随着理论的不断完善，小波变换已逐渐在信号处理、图像处理、地震勘探和医疗等众多领域得到广泛应用。

连续小波变换（Continuous Wavelet Transform，CWT）是一种积分形式的小波变换。对于平方可积的任意信号x(t)，其连续小波变换定义为：

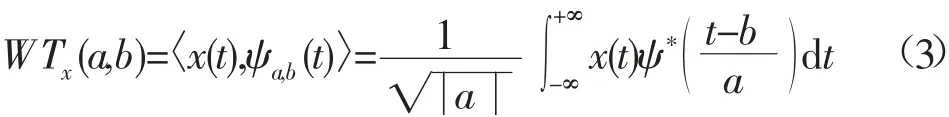
式中：ψ (t) 为基本小波函数或母小波函数；a，b分别为尺度（伸缩）因子和平移因子，a，b∈R，且a≠）的共轭形式。

对伸缩因子a和平移因子b进行离散化处理，一般取(m，n为整数，a0≠1)，得到母小波函数的离散形式：

对应的离散小波变换（Discrete Wavelet Transform，DWT）定义为：

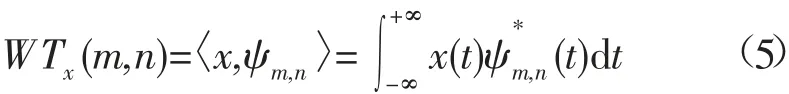
关于小波变换的详细理论，可以参见文献[9]，本文不再做具体论述。

1.3 希尔伯特-黄变换

1998 年，Norden E. Huang 提出了一种基于希尔伯特（Hilbert）变换的信号处理方法，后被称为希尔伯特-黄变换（Hilbert-Huang Transform，HHT）[10-11]。HHT 方法分为两个部分：经验模态分解（Empirical Mode Decomposition，EMD）和希尔伯特谱分析。

HHT 方法首先采用EMD 将信号分解成一系列的固有模态函数（Intrinsic Mode Function，IMF），这个过程被称为“筛选”过程。信号x(t)经过EMD 分解后可以表示为：

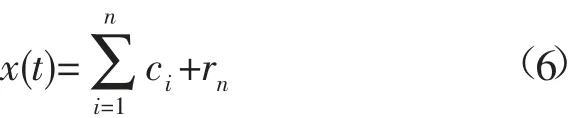
式中：ci表示第i个IMF；rn为残余函数，通常是一个恒定值或者单调函数。

对EMD 分解后得到的每一个IMF 做希尔伯特变换，将信号x(t)表示为：

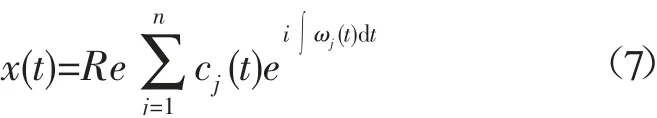
这里省略了残余函数rn；Re表示取实部；ω(t)表示t时刻的瞬时频率。将式（7）的右半部分定义为信号的希尔伯特谱，记为：

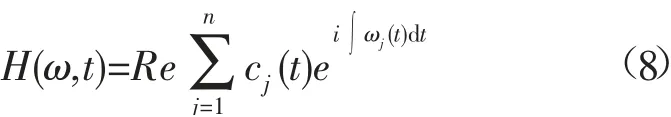
希尔伯特谱表示了信号的瞬时振幅在时间-频率平面上的分布情况。将希尔伯特谱在时间域上求积分，得到希尔伯特边际谱，记作：

希尔伯特边际谱描绘了在某一频率下，信号各分量的幅度（能量）之和，反映了各频率上的能量分布。

2 信号处理方法对比

前述方法具有各自的优势，在振动信号处理和特征提取中发挥了重要的作用。但是，各个方法也具有明显的局限性，适用范围不尽相同，在一定程度上限制了信号处理的效果。本文对各信号处理方法的优缺点及适用范围进行了汇总对比，如表1 所示。

表1 振动信号处理方法的对比

3 振动信号处理方法在导管架平台健康监测中的应用

3.1 傅里叶变换的应用

在导管架平台健康监测中，傅里叶变换是信号处理和特征提取技术的基础，但是由于傅里叶变换在分析非平稳信号方面的局限性，直接使用傅里叶变换进行信号处理以提取结构振动特征的研究较少。陈家宝等[17]通过直接对加速度响应进行傅里叶变换并计算相邻两点的传递率函数，以损伤前后的传递率函数的变化为依据，构造损伤指标D，D值最大处对应的结构即为发生损伤的结构位置。数值模拟和振动台试验的结果表明，该方法是可行的，且具有一定的抗噪声能力。以图1 为例，作者通过降低4 号支撑的刚度模拟结构损伤，计算各支撑的D值可以发现，4 号支撑的D值最大，这与假设是一致的。

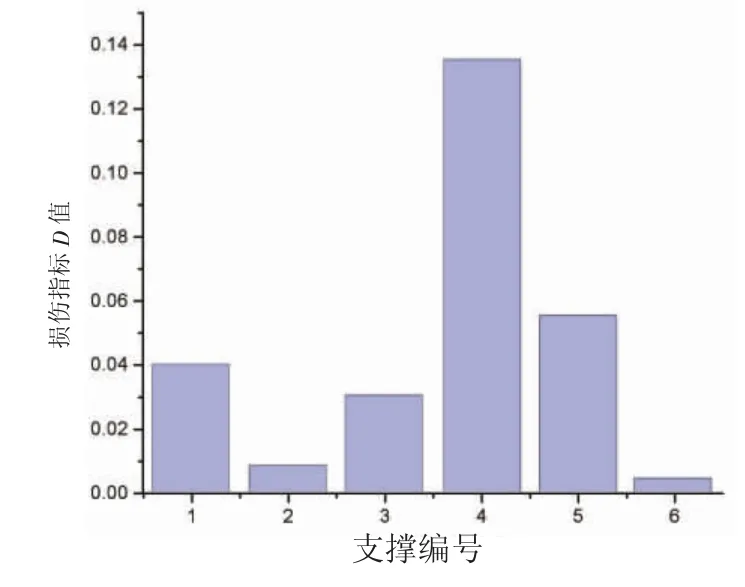
图1 4 号支撑损伤时各支撑的D 值[17]

此外，李洪涛等[18]利用细化快速傅里叶变换方法对完好与损伤状态下的导管架平台振动数据进行处理，分析幅值变化率与损伤位置之间量化的对应关系，从而实现在导管架平台的垂直方向上对损伤位置进行定位。Liu 等[19]提出了一种改进的模态参数识别方法，使用快速傅里叶变换滤波分离出低阶频率，重构出只由低阶频率组成的新的响应，利用新的响应重建特征系统实现算法（ERA）块数据矩阵来实现噪声模式的消除，提升了海洋导管架平台模态参数识别的精度和效率。

3.2 小波变换的应用

小波变换作为信号时频分析的有效方法，具有多分辨率的特点，可以显示信号的局部特性，因此，小波变换及其改进方法在导管架平台健康监测和特征提取领域得到了广泛应用。张兆德和王德禹[20]利用数值计算得到频响函数作为检验结构断裂情况的参数。对频响函数进行小波变换，可以发现早期结构损伤。李东升[21]以损伤前后小波变换系数作为损伤指标，对损伤前后位移模态振型差进行小波变换处理，通过小波变换系数的变化进行损伤定位；通过对频响函数进行连续小波变换，检测导管架平台结构是否存在小损伤。林裕裕等[22]通过导管架平台的数值计算，验证了基于小波变换损伤检测方法的有效性。同时，探究了局部超静定结构、噪声污染以及振动响应的方向对该方法的影响。闫东旭[23]使用小波分析进行导管架平台的损伤识别，发现小波变换对突变损伤的识别效果较好，但无法识别微小的渐变累积损伤；并且，小波包能量变化率指标具有非常好的损伤定位效果。李晔[24]对导管架平台的结构动力响应数据进行小波变换，提出了基于小波包能量变化的SAD 损伤识别指标，可以进行结构损伤时间和位置的精确识别。作者建立了导管架平台的ANSYS 模型，通过降低结构刚度模拟损伤，利用标准化的SAD 方法检测了不同损伤范围内的损伤位置，结果表明，该方法对不同损伤范围的情况仍然有比较好的定位能力，如图2 所示。Li 等[25]提出了地震的有效能量输入和有效能量输入率的定义，并利用小波变换得到地震的总有效能量和瞬时有效能量输入率，用以预测地震的临界发生率，进而计算导管架平台的最大动力响应。数值计算结果表明，小波变换在处理多分量地震响应中具有巨大的潜力。Asgarian 等[26]研究了导管架平台模型在不同损伤条件下的试验结果，利用小波包变换计算所有损伤情况下的信号能量率（RSE）用于损伤检测和损伤定位，结果表明，该方法能较准确地预测损伤位置。

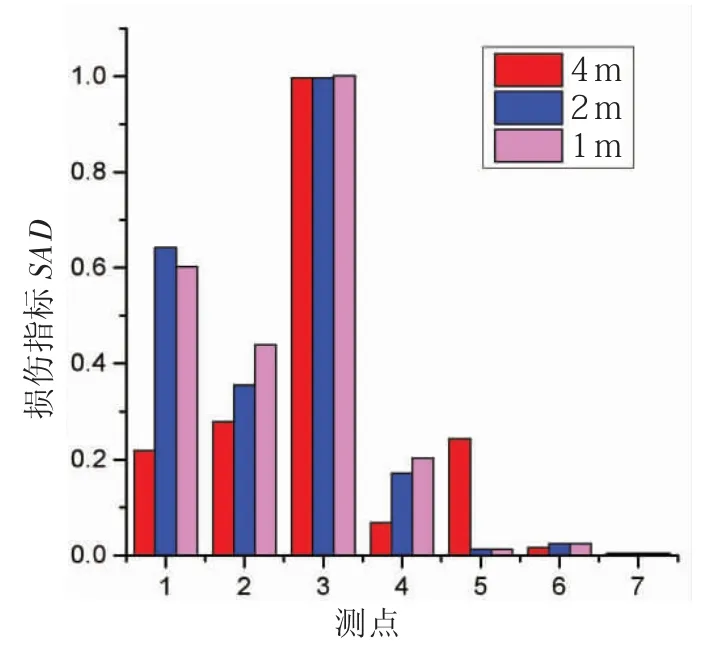
图2 SAD 损伤识别指标检验结果[24]

近年来，随着人工智能算法的快速发展，许多学者将小波变换与人工智能方法相结合，用于检测导管架平台的结构损伤。研究表明，小波变换结合人工智能的方法在导管架平台健康监测中能够取得很好的效果。刁延松[27]利用小波分析进行导管架平台的健康监测，并将小波包分解与RBF 神经网络、概率神经网络、BP 神经网络相结合，以确定损伤构件所在的方向、层位置以及损伤程度，数值模拟结果验证了方法的有效性。王典鹤[28]提出了基于小波细节信号结点能量的导管架平台结构损伤检测方法，提取小波分解的第二层细节信号结点能量作为概率神经网络输入，通过模型试验和数值计算，验证了该方法的有效性，并发现该方法具有一定的抗噪能力，但受到激励力方向的影响较大。陈明璐[29]将小波变换与BP 神经网络结合，通过对结构加速度响应信号进行小波包变换，提取各频带能量作为神经网络的输入，探究了应用该方法确定导管架平台结构损伤位置的能力，流程图如图3 所示。Diao等[30]利用白噪声作用下的两个节点的结构响应来计算虚拟脉冲响应函数，应用小波包分解获取节点能量，利用BP 神经网络，以损伤前后小波包节点能量变化作为损伤特征向量，确定结构损伤位置。Diao等[31]还通过受损结构的加速度响应计算传递函数，利用小波包分解分析传递函数的幅度，构造小波包能量矢量作为损伤特征，采用支持向量机进行损伤位置和损伤严重程度的识别。

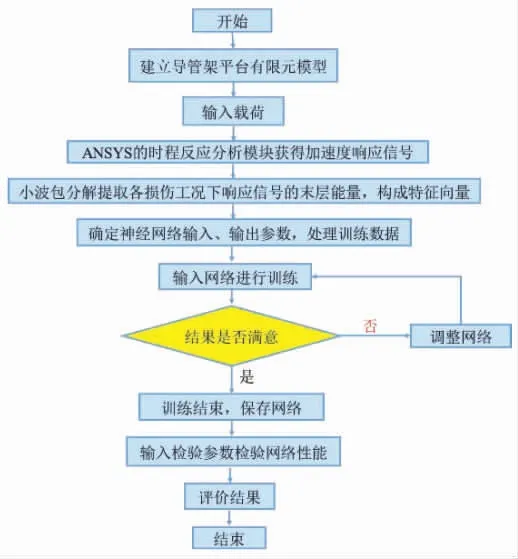
图3 小波包分析与神经网络相结合的损伤诊断方法流程图[29]

3.3 希尔伯特-黄变换的应用

希尔伯特-黄变换（HHT）是一种新兴的时频分析工具，无需选取基函数，具有自适应性，可以根据信号的局部时变特性进行时频分解，具有很高的时频分辨率，非常适合处理非线性非平稳信号。因此，HHT 在导管架平台健康监测中也取得良好的应用效果。

刘俊斐[32]利用HHT 进行了导管架平台的模态参数识别，针对有限元模型和实际结构的振动响应，分别使用采用傅里叶滤波器的HHT 方法和采用改进伪信号技术的HHT 方法识别其模态参数。结果表明，两种方法均能取得良好的效果，但相比之下，采用改进伪信号技术的HHT 方法的效果更佳。Dou[33]利用HHT 对WZ12-1 平台的监测信号进行故障特征提取，成功地揭示了WZ12-1 平台振动过大的原因。结果表明，HHT 可以作为故障特征提取的一种有效方法。Lin 和Chu[34]还利用HHT 方法提取声发射信号的瞬时频率和基于局部特性的能量特征，并与传统的声发射方法进行了比较。结果表明，该方法能够很好地进行声发射信号特征提取，是进行海洋结构裂缝识别的有效工具。

为了克服EMD 存在的不足，许多学者将HHT 方法加以改进，用于检验导管架平台的损伤。聂杰文[35]提出了一个基于低阶瞬时频率变化的损伤指标，利用数值模拟验证了该指标的有效性；提出HHT 与主成分分析结合的损伤检验方法，有效排除了温度对模态频率的影响；利用单立柱式和导管架式平台的有限元模型，探究了HHT 方法在不同损伤程度、不同外界激励下的损伤检测效果。华盼盼[36]提出了HHT结合AR 模型的方法，利用结构损伤前后AR 模型残差的方差之比构造结构损伤预警指标DI进行导管架平台的损伤识别。作者在非平稳激励作用下进行了5 组工况的损伤识别，分别为完好工况、损伤20%、损伤40%、损伤60%和损伤80%，如图4 所示。结果表明，模拟损伤工况的DI值全都大于1，且随着损伤程度的增加，DI值逐渐增加，证实了方法的有效性。岳槐宇[37]提出了基于EEMD 和统计控制图的损伤识别方法，利用各节点EEMD 能量熵值构建特征向量，多组特征向量组成能量熵样本总体，将每组特征向量到样本总体的马氏距离作为样本统计量建立X-bar 统计控制图，对结构进行损伤预警，通过数值模拟和模型试验，验证了方法的有效性。Lin 和Dou 等[38]采用EEMD 方法进行信号处理和分析，对采集到的WZ12-1 平台的甲板信号进行了检测，结果显示，该方法可以有效地识别导管架平台的故障。

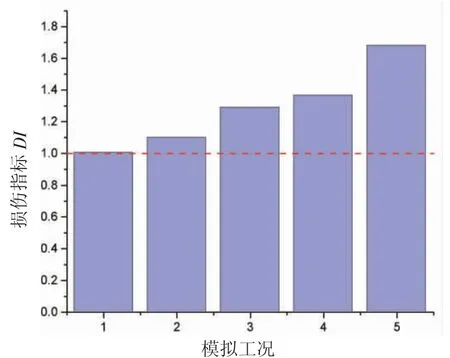
图4 非平稳激励下的损伤指标DI [36]

4 结论

通过以上对导管架平台健康监测中的振动信号处理方法的论述分析，可以得到以下结论。

（1）傅里叶变换方法简单、适用性强，短时傅里叶变换是对傅里叶变换的功能的改进和完善，二者对平稳信号都有很好的处理效果。但实际工程中得到的信号大多为时变的非平稳信号，限制了傅里叶变换的使用。

（2）小波分析和希尔伯特-黄变换都在非平稳信号的分析中取得了很好的效果，但仍然存在一定的缺陷。小波分析由于基函数的局限性，无法准确描述频率随时间的变化。希尔伯特-黄变换仍然存在端点效应、模态混叠等不足。

（3）在导管架平台健康监测和特征提取中，由于小波变换和希尔伯特-黄变换在信号处理中的优越性，因此相关研究较多，研究成果较为丰富。

随着科学技术的进步和相关领域的发展，上述振动信号处理方法将逐步得到发展和完善。在未来导管架平台振动特征提取的研究中，应当关注将多种振动信号处理方法结合使用，以弥补单一方法缺陷。同时，随着人工智能算法的不断发展，可以考虑将上述方法与人工智能方法结合使用，以期取得更加理想的信号处理和特征提取效果。