高中生数学建模能力发展状况调查研究—— 以核心素养为视角

唐丽艳

（深圳实验学校 中学部，广东 深圳 518026）

1 问题提出

《高中数学课程标准（2017 年版）》（以下简称《课程标准（2017 年版）》）中凝练了数学学科核心素养，六个数学学科核心素养在数学学科本质上蕴涵了六种数学关键能力，《普通高中课程方案（2017 年版）》的培养目标也突破了对数学知识的考察，开始由知识取向的评价走向能力取向的评价，这种能力就是数学学科核心素养下的数学关键能力。在2019 年的高中数学教育中已经开始对数学关键能力进行测评。本研究主要基于高中生数学建模能力，旨在解决如下问题：第一，高中生数学建模能力整体水平如何；第二，高中生数学建模能力在横向维度与纵向水平的整体状况如何；第三，不同年级之间学生的数学建模能力在横向维度是否存在差异；第四，不同年级之间学生的逻辑推理能力在纵向水平是否存在差异。这些问题的解决，可以在一定程度上为高中生数学建模能力的培养与评价提供数据支撑与策略引导。

2 数学建模能力测评的研究述评

数学建模能力测评的相关研究主要集中在以下几个方面。

第一，关于数学建模能力模型研究，一般来说，可以根据其水平划分，将其概括为“三水平模型”“四水平模型”与“多水平模型”三类。“三水平模型”采用低、中、高水平对数学建模能力进行刻画。很多国家课程标准均采用三水平划分方式，如我国《课程标准（2017 年版）》和德国《高中数学教育标准》都将数学模型划分了三个水平，但是两者又有所不同。前者从情境与问题、知识与技能、思维与表达、交流与反思四个层面对数学建模素养划分[1]，后者更侧重情境的转变，从给定的情境（水平Ⅰ）到变化的情境（水平Ⅱ），最后到复杂的情境（水平Ⅲ）[2]。“四水平模型”采用不合格、合格、良好以及优秀进行刻画。例如PISA2012 提出数学化能力，即数学建模能力，并按照其发展阶段划分为0-3 四个水平[3]。林子植基于SOLO 分类法，结合《课程标准（2017 年版）》中关于数学建模水平的划分，将数学建模能力分为前模型、单结构模型、关联结构模型与拓展结构模型四个水平[4]，这与PISA2012 的划分有所不同，从学生的回答表现出发，对学生建模能力的水平进行概括。“多水平模型”泛指超过四水平的数学建模能力模型，例如，徐斌艳等根据数学建模过程的阶段将数学建模能力划分为五个水平[5]，徐斌艳通过中德学生建模能力比较，又将其拓展为六个水平[2]。

第二，数学建模能力构成要素研究。例如Galluzzo 给出了数学建模的关键要素，即确定问题、作出假设、定义变量、获得解决方案、分析与模型评价、报告结果[6,p193-194]。

第三，数学建模能力的评价方式研究。评价方式有很多种，例如Frejd 测试题评价法、动手模拟评价法、建模项目评价法、档案袋评价法和建模竞赛评价法[7]，目前的研究以结果性评价为主，例如Galluzzo 构建一份数学建模评价量表，并据此评价学生数学建模能力[6,p193-194]，Lingefjärd &Holmquist 比较了同伴评价和家庭作业两种建模能力评价方法的异同[8]，徐斌艳等以“缝制足球”为例调查了我国6-9 年级学生的数学建模能力[5]。

3 数学建模能力分析框架的构建

《课程标准（2017 年版）》指出，数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构造模型解决问题的素养。从数学关键能力的视角来看，数学建模的外显能力表现包括：“在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题。”[9]根据《课程标准（2017 年版）》中关于数学建模素养水平的阐述，交流与反思更多需要在课堂教学中进行观察，为了便于分析学生数学建模能力与《课程标准（2017 年版）》之间的一致性，从《课程标准（2017 年版）》中数学建模的能力视角出发，对以上关于数学建模能力测评的相关研究进行梳理、总结与概括，选取可量化测评的水平描述，构建了本研究数学建模能力分析框架，横向维度考虑数量关系与空间图形，纵向水平涵盖模仿与举例、构造与求解、转译与检验三个水平。表1为三个水平的划分结构，其操作简单，便于对学生数学建模能力进行测评，受到国内外学者和机构的大力支持和广泛运用。

表1 高中生数学建模能力纵向水平分析框架

3.1 研究假设的厘定

本研究基于以下两个假设：其一，高中生数学建模能力的发展在一定程度上会受到年级的影响，学生数学建模能力会随着年级的升高而改变，教师专业素养、教学风格以课外辅导等因素不在本研究考虑范围之内；其二，高中生数学建模能力的高低可以通过学生测试卷的总平均分来反映，得分越高说明其数学建模能力越强，学生数学建模能力整体状况还受到各维度测评状况的影响。

3.2 研究方法的确定

根据分析框架与研究假设，本研究主要采用专家咨询法与问卷调查法。借助专家咨询法对初构的水平进行修订、检验，确保其科学性与合理性。专家结构包括高等院校的数学教育理论研究者、中学教研员以及教学一线的专家型教师，这样的结构对于高中生数学建模能力水平的划分既有理论的指导，又能从教学实践出发，符合学生在实际学习中的表现。问卷调查法是为了探究高中生数学建模能力发展状况，确定高中生数学建模能力达成情况，考察不同年级的学生的数学建模能力在横向维度与纵向水平的具体表现。

3.3 测评问卷的编制

本研究通过对已有测试题目的甄选与改编，形成高中生数学建模能力测评问卷并对其进测评，在测评问卷开发过程中，根据题型设计的基本原理与题项选择的基本原则。由于本研究测量高中生数学建模能力，这是一种综合型数学关键能力，注重学生的模仿与举例、构造与求解、转译与检验，更多反映学生的思维过程，考察学生在实际情境中解决问题的能力，而非简单的知识记忆和技能训练，因此，所选题型与题项依据《课程标准（2017 年版）》要求控制题项难度，依据教学内容减少知识干扰，依据学生特征确定题项来源，依据水平划分调节题项梯度。除此之外，对高中生数学建模能力进行测评的难点还在于，不能单纯以学生所学知识为载体，这样难以体现其建模能力，所以，尽量选取与所学知识相关不大的内容编制测试卷，以主观题为主，经过三次调整，最终形成测评问卷，问卷中包含18 个测评题项，每个水平设计3 个题项，数量关系与空间图形各9个题项。

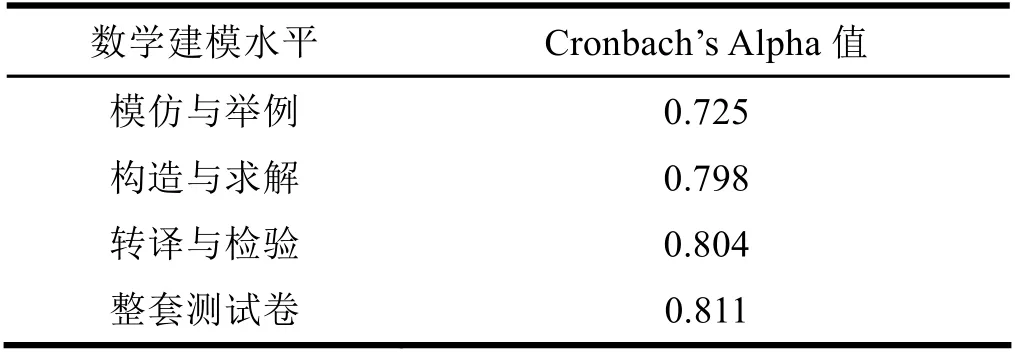
表2 各年级测评问卷信度表

在正式施测之前，对测评问卷的信度与效度进行检验。测评问卷的信度可见表2，各水平题项信度均大于0.7，问卷年整体信度大于0.8，测评问卷的ɑ信度指标基本达到了测量学要求，各分测评之间具有很高的一致性，适宜作为测量工具进行团体测量。

效度主要考察内容效度与结构效度，在内容效度上，采用专家咨询的方式，结合一线特级教师的教学经验来提升内容效度。在结构效度上，采用因素分析法，测评问卷旋转后的因素负荷矩阵和累积解释变异量表明，提取的三个因素（模仿与举例、构造与求解、转译与检验）的特征值分别是2.751、2.134、1.672，累积解释变异量为61.127%，对整个测评问卷的有效程度较好，数学建模能力三个水平的结构具有很好的稳定性和独立性，问卷的内部结构较为理想，其建构效度较好。

通过相关分析来检验各水平之间是否存在相关性，相关系数矩阵如表3 所示。结果显示，三个水平之间的相关系数在0.419～0.612 之间，表现为中等相关。各水平与问卷总体的相关系数在0.533～0.738 之间，均表现为中等相关或强相关，达到测评标准。

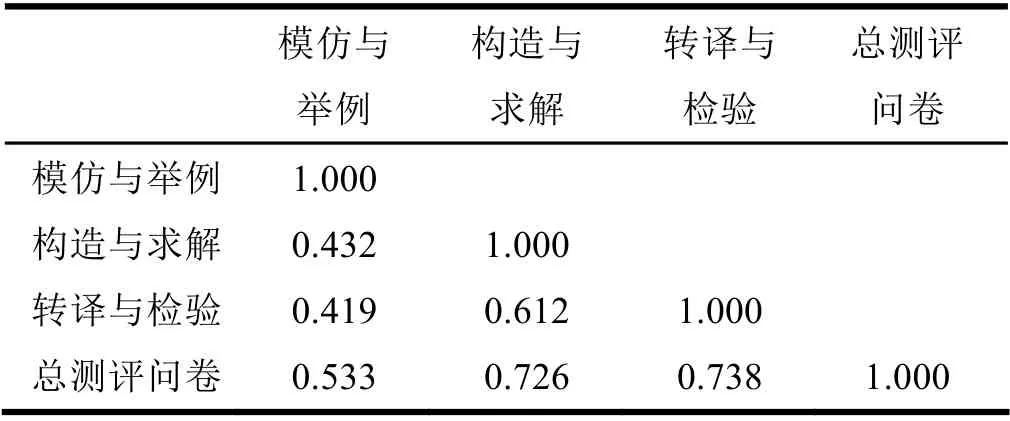
表3 各水平之间的相关系数矩阵

3.4 研究样本的遴选

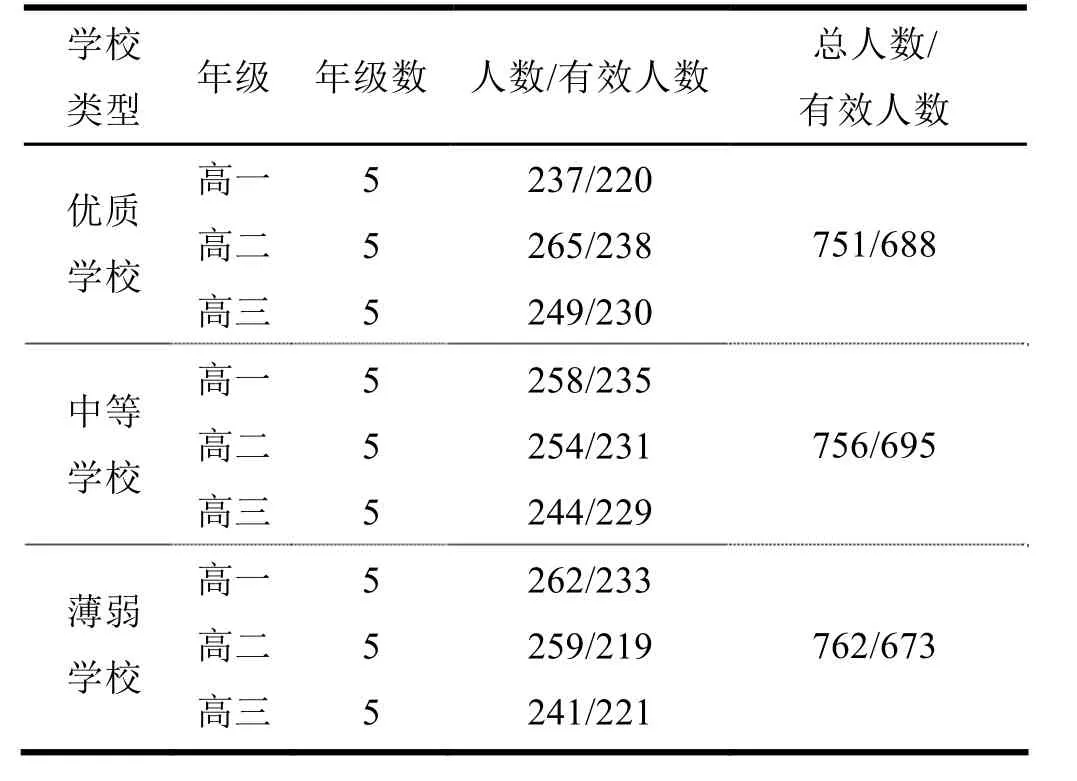
表4 高中生样本分布表

考虑样本的代表性与方便性，以唐山、承德、石家庄、衡水、张家口等为样本城市，根据每个样本城市学校的生源水平、师资状况、软件条件、硬件设施、学校管理等因素，将样本学校分成三类：一类是优质学校，二类是中等学校，三类是薄弱学校。每个样本城市选取3 所样本学校，再从每类样本学校中选取高一至高三的中等年级的学生作为测试对象，共发放测评问卷2 269 份，回收测评问卷2 269 份，有效问卷2 056，有效率是90.6%，学生样本分布如表4 所示。

3.5 数据分析的标准

本次调查采用现场测评的方式，由于考虑高考复习的影响，高三年级学生在第一学期期末进行测评，高一、高二学生在第二学期期末进行测评。测评时长为50 分钟，整个测评过程中，教师不能对学生进行指导或提示，学生测评问卷的评分由一名高校教师和两名高中数学教师共同完成。每道测评题项最低分为0 分，最高分为5 分，包含0、1、2、3、4、5 六个分值，问卷满分为90 分。评分方式采用相互独立评分与仲裁相结合，先由两名高中数学教师独立完成评分，如果出现分歧较大的题项或者分数，再由第三名教师进行仲裁，教师评分在95%以上一致，一致性程度较高。

4 研究结果

本研究主要利用SPSS22.0 进行数据处理，主要得到以下研究结果。

4.1 高中生数学建模能力的发展态势

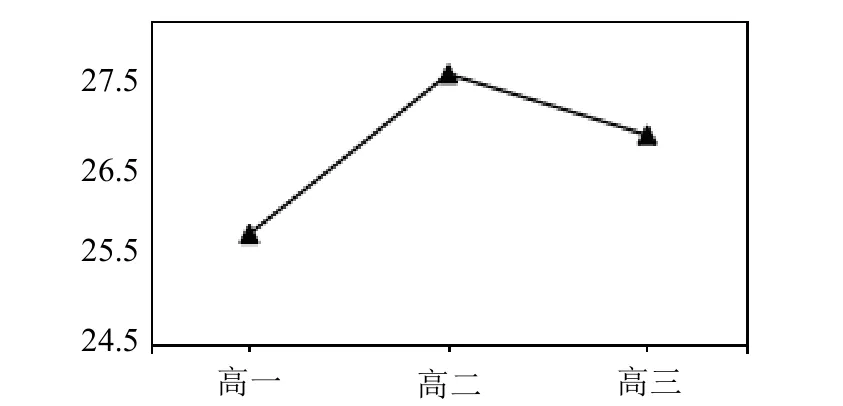
图1 高中生数学建模能力整体发展状况图

由图1 可以发现，高中生数学建模能力整体呈现先增后降的发展趋势，高一年级学生的平均分是25.69 分，高二年级学生的平均分是27.42 分，高三年级学生的平均分是26.76 分，三个年级学生的得分均未达到合格标准（满分为90 分，合格分数为54 分）。三个年级学生数学建模能力的得分率分别是28.5%、30.4%、29.7%，高二年级学生得分率最高，高三年级得分率次之，高一年级得分率最低，三个年级学生在数学建模能力整体得分均不高。

4.2 高中生在横向维度与纵向水平的发展态势

4.2.1 高中生数学建模能力在横向维度上的发展态势

从图2 可以看出，高中各年级学生数学建模能力在空间图形维度的得分要高于数量关系维度的得分，在两个维度上均表现为高二年级学生得分最高，高三年级学生得分次之，高一年级学生得分最低，与学生整体发展状况相吻合。在两个维度上，高中生数学建模能力呈现先增后降的发展趋势。在空间图形维度上，三个年级得分分别为13.04、14.11、13.61，得分率分别为29.0%、31.4%、30.2%，三个年级学生在空间图形维度得分率在30%左右，得分率较低；在数量关系维度上，三个年级得分分别为12.65、13.31、13.15，得分率分别为28.1%、29.6%、29.2%，得分率很低。

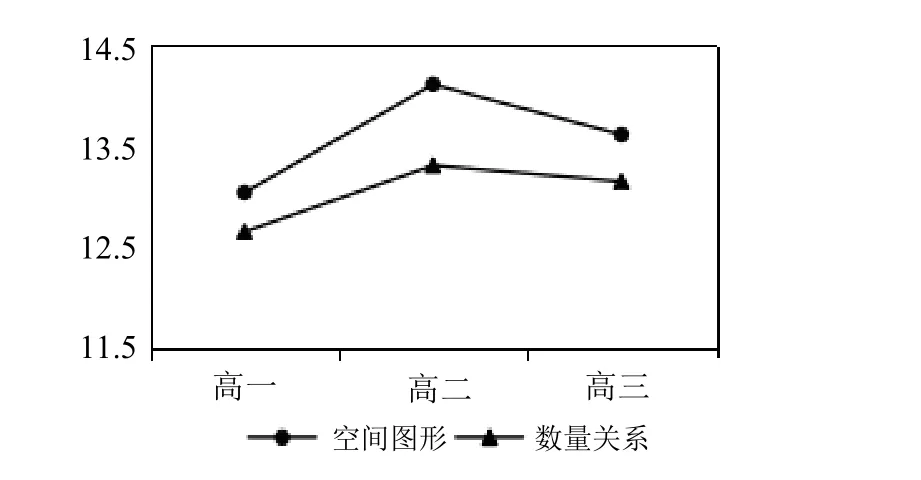
图2 高中生在数学建模能力横向维度上的发展状况图

4.2.2 高中生数学建模能力在纵向水平上的发展态势

从图3 可以看出，高中生数学建模能力的测评成绩随着发展水平的升高而递减，模仿与举例水平测评成绩最高，构造与求解水平测评成绩次之，转译与检验水平测评成绩最低。在模仿与举例、构造与求解两个水平上，三个年级学生数学建模能力测评成绩呈现先增后降的发展趋势；而在转译与检验水平上，三个年级学生数学建模能力测评成绩随年级的升高而增长；在模仿与举例水平上，三个年级学生数学建模能力测评成绩依次是11.44、11.67、10.91，得分率分别为38.1%、38.9%、36.4%；在构造与求解水平上，三个年级学生数学建模能力测评成绩依次是8.10、8.68、8.28，得分率分别为27.0%、28.9%、27.6%；在转译与检验水平上，三个年级学生数学建模能力测评成绩依次是6.15、7.07、7.57，得分率分别为20.5%、23.6%、25.2%。

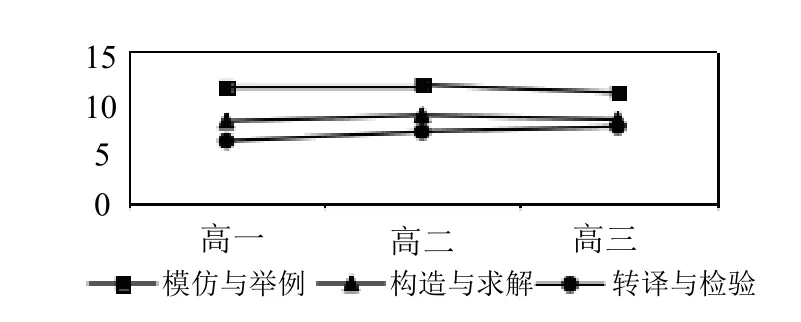
图3 高中生数学建模能力在纵向水平上的发展状况图

4.3 不同年级学生的数学建模能力在横向维度上的差异

为了更好地理解高中生在数学建模能力横向维度的表现状况，我们对高中三个年级学生得分进行方差分析，结果如表5 所示，不同年级学生的数学建模能力在数量关系与空间图形上存在显著差异。进行t 检验，结果表明，高一年级学生与高二年级学生在数量关系（t=-8.72，P＜0.05）、空间图形（t=-8.40，P＜0.05）上存在显著差异，高二年级学生与高三年级学生在数量关系（t=-1.91，p＞0.05）上不存在显著差异，在空间图形（t=-3.73，p＜0.05）方面存在显著差异。

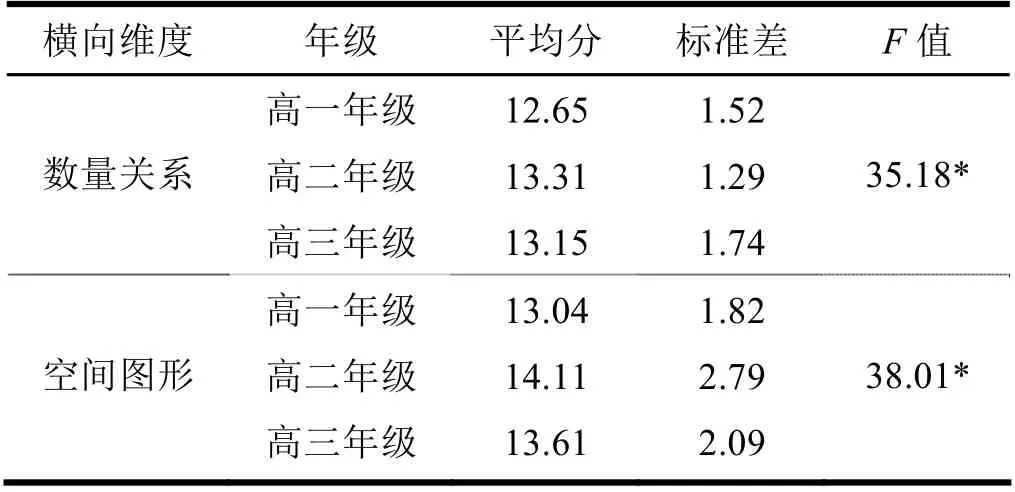
表5 不同年级的学生在横向维度上的差异

4.4 不同年级学生的数学建模能力在纵向水平上的差异

为了了解不同年级学生在数学建模能力纵向水平上的差异，对三个年级学生的纵向水平得分进行方差分析，如表6 所示。不同年级学生的数学建模能力在数量关系与空间图形上存在显著差异。进行t 检验，结果表明，高一年级学生与高二年级学生在模仿与举例水平（t=1.33，p＞0.05）上不存在显著差异，在构造与求解水平（t=2.53，p＜0.05）、转译与检验水平（t=4.64，p＜0.05）上存在显著差异，高二年级学生与高三年级学生在构造与求解水平（t=1.95，p＞0.05）上不存在显著差异，在模仿与举例水平（t=3.99，p＜0.05）、转译与检验水平（t=2.72，p＜0.05）上存在显著差异。

表6 不同年级的学生在纵向水平上的差异

5 研究结论与讨论

5.1 高中生数学建模能力发展状况不理想

高中生数学建模能力发展水平呈现先增后降的发展趋势，从测验的得分率来看，高中生数学建模能力得分偏低（28.5%、30.4%、29.7%），整体发展水平并不理想。这与一些研究所取得的结果是一致的，高中生数学建模能力依然是学生的薄弱之处，这可能与学生疏于从事实际问题解决有关。在传统课堂中，多以基础知识与基本技能作为教学重点，所涉及的问题情境也是“去情境化”的“理想情境”，导致学生难以从复杂的情境中获得有用的信息，这是导致学生数学建模能力偏低的一个原因。除此之外，学生的创新意识与迁移意识的缺乏也是其数学建模能力偏低的重要原因，学生整体构造能力较差，难以构建数学模型，这与高中数学课程设置、教学实施、评价方式等有关。因此，如何培养高中生的数学建模能力仍然是我国目前数学教育中亟待解决的重要问题。

5.2 高中生数学建模能力在各水平上呈现非均衡性

高中生数学建模能力在模仿与举例、构造与求解、转译与检验三个水平上呈现非均衡发展。从测评成绩来看，模仿与举例水平远远好于构造与求解水平、转译与检验水平。高中生在模仿与举例、构造与求解、转译与检验三个水平的平均得分率分别是37.8%、27.8%、23.1%，可以看出，达到模仿与构造水平的学生将近五分之二，学生更多的是模仿、借助所学模型解决简单问题，对于举例说明建模的意义及其所蕴含的数学思想表现不够好。达到构造与求解、转译与检验两个水平的学生均不足三分之一，在这两个水平中，对于学生较难的是构造、检验，构造是整个数学建模的内核，要求学生能够从现实世界中发现关系，并建立模型，而检验的效果较差可能与高中数学应用题的教学有关，高中应用题教学强调如何建立模型解决问题，一般不会给学生提供检验的机会和空间。

5.3 高中生数学建模能力的培养滞后于课程标准

在研究中我们发现，大部分学生数学建模能力依然处于初级阶段，数学建模的重要性仍未引起教师与学生的重视，这也侧面反映出课程标准在教学落实中的缺失，高中生实际数学建模能力与《课程标准（2017 年版）》中对数学建模的要求相差甚远。从学生在数学建模能力测评中的表现，可以很清楚地看到这一点，一方面，学生在数量关系与空间图形两个维度的平均得分率仅为30.2%和29.0%，两个维度表现均较弱；另一方面，高中生数学建模能力在模仿与举例、构造与求解、转译与检验三个水平的表现差异较大。目前问题解决是课程变革所强调的重要内容，而数学建模是数学问题解决的重要能力，因此，高中生数学建模能力的培养要紧跟《课程标准（2017 年版）》的要求，关注高中数学课程改革的变化，使高中生在数学建模能力的发展上与国际数学教育保持同步。