基于凸模型的T-S 因果图分析
李莉莉,段吉莲
(重庆师范大学 数学科学学院,重庆 401331)
因果图模型是张勤提出的一种基于概率论的不确定性推理方法[1]。因果图采用图形来表示因果关系,是由逻辑门符号和各种事件组成的。传统因果图中的逻辑门通常采用布尔逻辑门,逻辑门用来描述事件间的联系。事件的发生往往具有不确定性,通常用概率模型和模糊模型描述不确定性,但发现凸模型更容易处理未知但有界的不确定性问题,凸模型包括区间凸集模型和超椭球凸集模型。
在实际工程中,复杂系统发生故障方式复杂多样,事件间的联系再用布尔逻辑门来描述,就显得不准确。文献[2]将T-S 模糊门引入到因果图中,利用T-S 模糊门描述事件联系更为一般化和精确化。统计事件发生故障的原因时,数据往往不精确,甚至缺乏。因此难以用精确的概率模型来描述事件,王洪春等人将模糊数引入到因果图中,提出了模糊因果图[3],在故障分析和故障诊断两方面都有很好的应用。虽然很难获取不确定变量的模糊隶属度函数,但其边界却容易获得,为此将凸模型与T-S 因果图相结合,提出基于凸模型的T-S 因果图方法,包括基于区间模型的T-S 因果图和基于超椭球模型的T-S 因果图分析方法。
1 凸模型T-S 因果图
1.1 区间T-S 因果图


由此二维区间模型及上式可以分析出,要得到上级事件发生的概率边界值,必须同时取基本事件的发生概率区间的边界值才能满足。但这种情况非常极端,是很难发生的,因此区间T-S 因果图这种分析方法太过于保守,与实际冲突。
1.2 超椭球T-S 因果图
为解决区间模型描述事件的不足,采用超椭球模型对区间进行约束。对比于区间模型,超椭球模型把区间变量的一些取值区域排除,使之更符合工程实际,形成超椭球T-S 因果图分析法:基本事件发生的区间概率用


2 实例
当复杂系统对应的因果图中的一个或多个基本事件发生时,随着各个事件发生的故障程度的不同,则对应的中间事件可能发生故障也可能不发生故障,即发生故障的可能性具有不确定性,难以用传统的布尔逻辑门来表示因果图中事件的联系,将T-S 模糊门和凸集模型应用到因果图中。
图1 是某动力系统因果图[8],转化成T-S 因果图如图2,其中 T,A,B1,B2,B3分别表示动力系统,液压泵,调压块,插装阀,电磁流。

图1 动力系统因果图
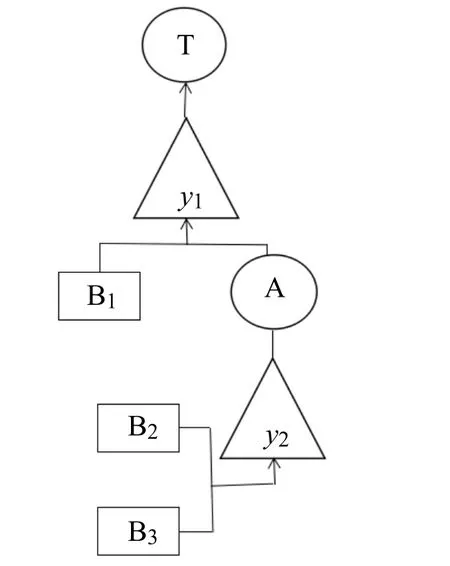
图2 T-S 模糊门因果图
假设中间事件和顶事件有三种状态:可能不发生故障、一半的可能发生故障和完全发生故障,用0、0.5、1 表示这三种状态,且基本事件 B1, B2,B3发生故障程度为1 的概率区间分别为

故障程度为0.5 的概率区间相同。根据历史数据和专家经验构造T-S 门规则表。

表1 T-S 模糊门1

表2 T-S 模糊门2
表中的每一行代表一条规则,例如表1 中第6行规则表示:若2B 不发生故障,3B 半故障,则1y 为0 的概率为0.2,为0.5 的概率为0.3,为1 的概率为0.5。
利用基于区间模型的T-S 因果图分析方法,得到事件的区间概率为


由上可见,超椭球T-S 因果图分析方法得到的概率区间包含在区间T-S 因果图分析方法得到概率区间中,解决了区间T-S 因果图分析计算结果相对保守的问题。
3 结论
在大型的复杂系统中,由于缺乏部分历史数据,事件间的联系也是十分不确定的,采用T-S模糊门描述事件间的联系,解决建立因果图模型时精确数据难以获取的问题。将描述事件的凸集模型应用到因果图中,并由某动力系统因果图进行实例分析发现超椭球T-S 因果图分析方法比区间T-S 因果图分析方法更符合实际。

