具有时滞的肿瘤免疫模型的稳定性与Hopf分支*
梁雨琴, 贾云锋
(陕西师范大学数学与信息科学学院, 陕西 西安 710062)
肿瘤是生物体器官局部组织的细胞在生长过程中失去了生长的正常调控或受病毒感染而发生的以细胞异常增生、过度增殖为主要特点的新生物。临床医生和肿瘤学家认为, 肿瘤细胞生长、增殖、转运和免疫应答具有不可预测的动态, 因此, 人们在治疗癌症方面遇到了许多困难。 近三、四十年来, 数学模型已逐步成为人们认识复杂的肿瘤系统的重要工具。自从Stepanova[1]提出经典的肿瘤免疫模型以来, 各种肿瘤免疫模型相继被建立并取得了许多有价值的研究成果[2-12], 这些成果对恶性肿瘤的研究具有重要的理论与临床意义。最近,文献[13]中研究了一类具有时滞和扩散项的生物模型, 研究结果表明:物种的扩散行为会影响系统的稳定性, 扩散和时滞的结合可以导致并加剧系统的不稳定性。由于生物体本身具有免疫功能, 生物体内的免疫细胞能够识别并消除肿瘤细胞, 文献[14]中研究了一类具有时滞的肿瘤免疫模型, 结果表明:时滞会影响系统的稳定性, 适当调节时滞参数可以控制恶性肿瘤的生长。事实上, 由于生物体的免疫系统在识别非自身细胞后需要一定的时间来产生合适的免疫反应, 因此, 在研究肿瘤问题时将时滞因素引入到具体的数学模型中是合理的。同时, 从生物学角度来看, 肿瘤细胞与免疫细胞的生长、相互作用不仅与时间有关, 也会受到空间因素的影响与制约。受文献[13-14]中扩散、时滞可以导致并加剧系统的不稳定性结果的启发, 本文引入并研究具有时滞的肿瘤免疫反应扩散系统:
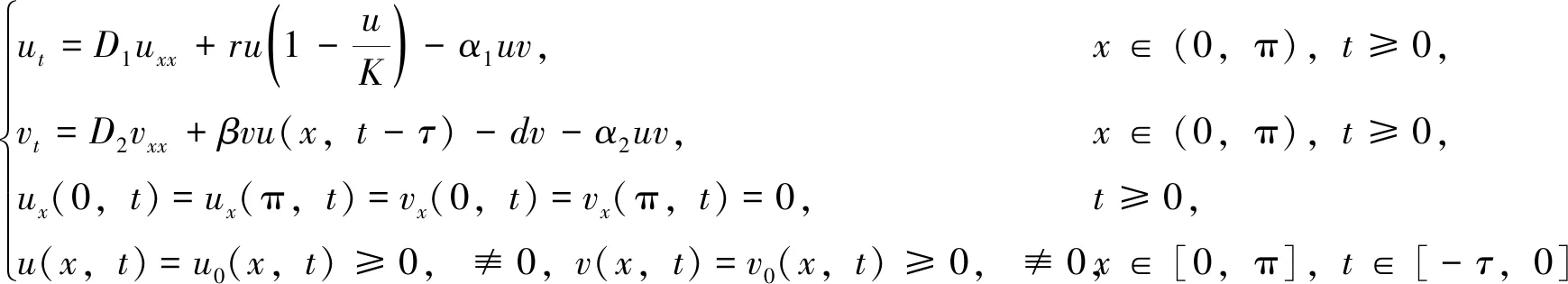
(1)
其中u,v分别表示肿瘤细胞数和免疫细胞的数量,D1和D2分别为u,v的扩散率,τ为时滞参数,r为肿瘤细胞的自然生长率,K表示环境最大承载能力,d是免疫细胞的自然死亡率,α1表示受免疫细胞攻击而减少的肿瘤细胞的死亡率,α2表示与肿瘤细胞作用而消亡的免疫细胞的死亡率,β为免疫细胞的活化率, 反应项βvu(x,t-τ)表示在肿瘤细胞的刺激下免疫细胞能够被激活、从而产生合适的免疫反应在时间上会有延迟。系统中所有参数均为正数。
1 边界平衡态解的稳定性
显然, ∀(x,t)∈(0,π)×(0,∞), 系统(1)存在边界平衡态解(K,0)。
定理1当d>Kβ时, 边界平衡态解(K,0)是全局渐近稳定的。
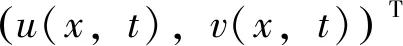
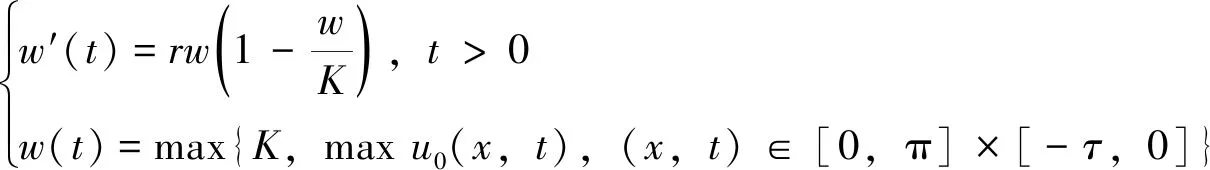
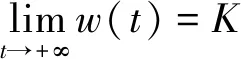
由比较原理知u(x,t)≤w(t),∀x∈[0,π],t≥0。于是有
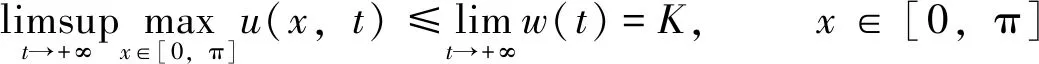
这样, 对充分小的正数ε, 存在t1=t1(ε)1使得u(x,t)≤K+ε,x∈[0,π],t≥t1。于是, 当t≥t1时, 有u(x,t)≤max{K,maxu0(x,t),(x,t)∈[0,π]×[-τ,0]}。这样, 由系统(1)的第二个方程知v(x,t)满足
这说明v(x,t)是问题
的下解。易知函数Ce(Kβ-d)t是该问题的上解, 其中C满足C>maxv(x,t1),x∈[0,π]。于是,v(x,t)≤Ce(Kβ-d)t,x∈[0,π],t>t1。由于d>Kβ, 因此有
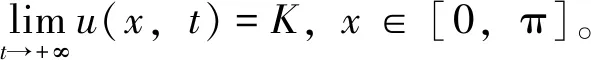
的解。那么, 对充分大的t2,φ(t)≡K是满足该问题中方程的唯一正解, 并且u(x,t)满足
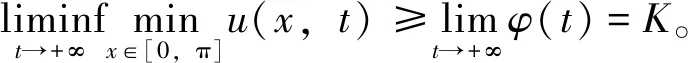
即边界平衡态解(K,0)是全局渐近稳定的。证毕。
2 正平衡态解的稳定性及发自正平衡态解处的Hopf分支的存在性

设
U(x,t)=(u(x,t),v(x,t))T∈Χ={(u,v)T:u,v∈W2,2(0,π),ux=vx=0,x=0,π}
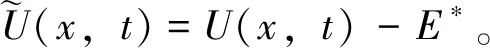
Ut=DUxx+A0U+A1U(x,t-τ)+G(U) (2)
其中D=diag(D1,D2),
众所周知, 一维Laplace算子在X上的特征值为-k2,k=0,1,2,…, 相应的特征向量记为
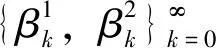
对φ=(φ1,φ2)T∈X, 简单计算表明
于是, 特征方程可写成
从而, 特征方程等价于方程:
λ2+Akλ+Bk+Cke-λτ=0,k=0,1,2,…
(3)
其中
(4)
定理2当τ=0时, 系统(1)的正平衡点E*是局部渐近稳定的。
证明当τ=0时, 特征方程(3)变为λ2+Akλ+Bk+Ck=0。这时,
设特征方程的两个根为λ1,λ2,则λ1+λ2=-Ak,λ1λ2=Bk+Ck。此时, 方程的两个根都具有负实部, 所以系统(1)的正平衡点是局部渐近稳定的。证毕。
固定参数r,K,α1,α2,β,d, 记
(5)
由于k+≥0,因此集合Τ非空。再记
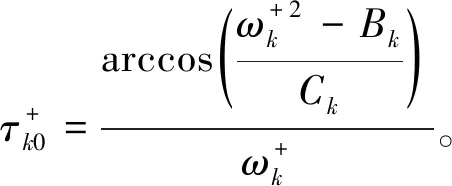
定理3
(i) 若k>k+, 则对∀τ≥0, 正平衡态E*是局部渐近稳定的。
(ii) 若k∈T, 则当τ∈[0,τ*)时,E*是局部渐近稳定的; 当τ>τ*时,E*是不稳定的。
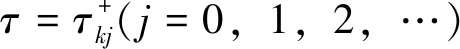
证明根据Hopf分支产生的条件, 不妨设±iω(ω>0)是特征方程(3)的一对纯虚根, 将其代入特征方程(3)中得
-ω2+iAkω+Bk+Cke-iωτ=0
分离实部和虚部可得
Ckcosωτ=ω2-Bk,Cksinωτ=Akω
(6)
计算可得
(7)
令z=ω2, 上式变为
(8)
其中Ak,Bk,Ck(k=0,1,2,…)由(4)式给出。
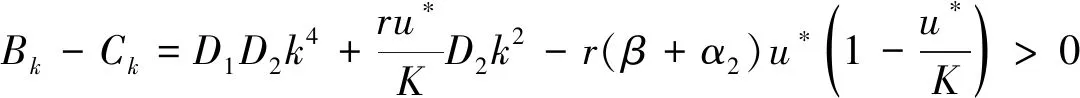
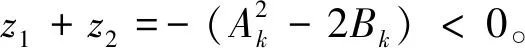
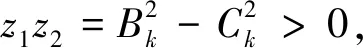


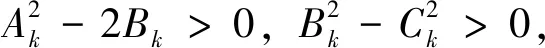
3 结 论
本文研究了一类具有扩散和时滞的肿瘤免疫模型。研究结果显示, 时滞对正平衡点的稳定性有着重要的影响, 正平衡点的渐近稳定性或不稳定性取决于时滞τ的大小, 存在一个临界值τ*, 使得当τ<τ*时, 正平衡点是稳定的; 当τ>τ*时, 正平衡态是不稳定的, 在正平衡点不稳时系统可能产生Hopf分支解。

