轨道交通不良地质风险动态可变评价模型研究*

武志毅，高燕，袁泉，李文龙

(1. 中山大学地球科学与工程学院，广东 广州 510275；2．广东省地球动力作用与地质灾害重点实验室，广东 广州 510275；3.广州地铁设计研究院股份有限公司，广东 广州 510010)

城市轨道交通以其节省地面空间、噪音较小、干扰较小、节约能源、污染较小以及速度快、准时、运量大等优点，在我国城市交通中占据越来越重要的地位。截至2017年末，中国(不含港澳台地区)开通轨道交通线路165条，开通城市共计34个，运营线路长度共计5 033公里。但是轨道交通面临的问题也很突出，如建造成本高、前期投入时间长、施工工艺要求高、施工面临的地质环境复杂。在轨道交通大量建设期间，国内各地均发生了不同程度的施工事故，给人民生命财产带来了严重损失。2007年3月28日，北京地铁10号线苏州街站出口工程发生坍塌事故，6名工人被埋。2013年1月28日，广州市荔湾区康王公交站地铁施工工地旁陆续出现六次坍塌，塌陷面积约690平方米。2018年2月7日，佛山市地铁2号线绿岛湖至湖涌盾构区间工地地面出现坍塌，致11死1失联。经过对事故缘由的分析，发现事故多与工程所处的地质环境有关。因此，对轨道交通不良地质环境的综合风险等级评价显得十分重要。

国内对于轨道交通隧道风险管理控制的研究始于20世纪80年代，黄宏伟阐述了风险的定义、发生的机理以及风险管理中存在的主要问题[1]。欧志坚采用可拓理论，建立了公路山岭隧道施工安全风险可拓辨识模型，对公路山岭隧道施工的风险进行了全面的辨识，并开发了公路山岭隧道施工的风险辨识系统[2]。娄荣祥等通过建立和分析地铁工程地下水风险评估模型，得出影响地下工程地下水风险的最重要阶段是施工阶段，并对此提出了有效的地下水风险防治措施[3]。周念清等基于模糊数学理论，以上海地铁10号线南京东路车站为例，评判了地铁工程地下水风险[4]。许振浩等为了控制岩溶地区隧道施工风险，研究了该地区的岩溶发育特征，以及隧道突水突泥施工风险的致险因子，首次提出了一种基于风险动态评估与控制的岩溶隧道施工许可机制[5]。李明基于隧道和地下工程运营阶段的结构变异、衬砌开裂等因素建立了健康动态诊断系统，实现了隧道和地下工程评价模型的可变性[6]。张萌针对地铁建设期间的土性、岩性等10个风险因素，建立了基于模糊综合评价法的风险评价模型[7]。郑晓静基于传统的专家判断矩阵赋权方法，提出了一种可以动态赋权的FUZZY-AHP评估模型[8]。赵文娟等采用有限元数值计算的方法，定性定量地研究了典型的上软下硬地层中隧道围岩的稳定性规律，并建立了典型上软下硬地层隧道围岩稳定性的定性定量化标准[9]。杨霖涛等运用乘积标度法对山岭隧道的塌方风险因素进行了赋权，建立了隧道塌方风险评估模型，详细叙述了隧道塌方风险的评估过程[10]。

目前大部分的研究都是针对公路隧道、山岭隧道的风险评估，少部分研究的对象为轨道交通隧道工程。比起公路隧道和山岭隧道，轨道交通隧道工程由于其位于经济相对发达的城市，隧道也多位于地下，线路也相对较长，施工工艺要求较高。因此，其地质环境更为复杂，风险辨识因子也不同，风险判定标准要求也更高。而少部分风险评价模型的研究对象虽然为轨道交通隧道工程，但也都是针对于轨道交通隧道工程运维期风险等级的评价，而不是针对轨道交通隧道全生命周期的风险评估。且风险评估模型大多是静态的。

本文通过查阅国内外大量文献、标准与现场调查，建立了包括围岩等级、复合地层、地下水、有害气体、特殊土、地震、断层、褶皱、地裂缝、岩爆、岩溶的11个不良地质风险源，40个辨识因子的风险评价因素集，涵盖了轨道交通隧道工程在设计、施工阶段所面临的地质风险、增加运维期的地质风险因素，实现了对轨道交通隧道工程全生命周期的风险评估。并辨析出每个辨识因子的Ⅰ(微风险)、Ⅱ(弱风险)、Ⅲ(中风险)、Ⅳ(强风险)四级风险评价标准。在此基础上，基于BP神经网络赋权和乘积标度赋权的组合赋权法，确定了针对轨道交通隧道不良地质的模糊可变评价模型。进一步，结合某些辨识因子的时间特性，建立了相应的考虑时间效应的动态评价模型。动态模糊可变评价模型具有动态性和可变性，不仅可以评价指定段隧道的地质风险等级，亦可获得对地质风险等级影响最大的一级指标和二级指标。

1 不良地质风险评价因素集

在城市地铁等轨道交通的设计与建设过程中，不可避免就会遇到各种复杂的地质条件，如围岩等级、溶洞、断层破碎带、复合地层、地下水等。根据国内的相关文献和国家标准，地质风险因素的选取应具备科学性、相对完备性、层次性、相对独立性与可比性。因此，本文对轨道交通不良地质风险源进行了辨识，划分为目标层、一级指标层、二级指标层三层，如图1所示。目标层包括11个一级指标，即11个轨道交通隧道工程不良地质风险源；一级指标层包括40个二级指标，即40个不良地质风险源辨识因子，进而建立了轨道交通隧道工程不良地质风险因素集，如表1所示。

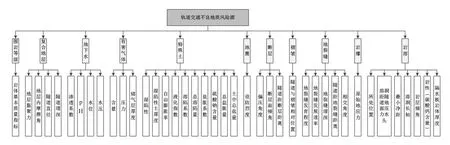
图1 轨道交通不良地质风险源辨识图

表1 不良地质风险评价因素集

续上表

特殊土湿陷土黄土湿陷性△s≤300且△ZS≤70△s>300且△ZS≤70;△s≤300且70<△ZS≤350△s>300且70<△ZS≤350;300<△s≤700且△ZS>350△s>700且△ZS>350湿陷性碎石土50<△s≤300且d>350<△s≤300且d≤3;300<△s≤600且d>3300<△s≤600且d≤3;△s>600且d>3△s>600且d≤3GB50025-2004,湿陷性黄土地区建筑规范[16]膨胀土自由膨胀率δef/%40～6060～7575～90>90GB 50112-2013,膨胀土地区建筑技术规范[17]液化土液化指数IIE0～66～1212～18>18GB 50011-2010,建筑抗震设计规范[18]盐渍土溶陷系数δrx0.01～0.020.02～0.030.03～0.05>0.05总溶陷量Srx/mm70～110110～150150～400>400盐胀系数δyz0～0.010.01～0.020.02～0.04>0.04硫酸钠含量Cssn/%0～0.50.5～1.21.2～2.0>2.0总盐胀量Syz30～5050～7070～150>150土中总盐量/(mg·kg-1)有蒸发面0～3 0003 000～5 0005 000～10 000>10 000无蒸发面0～5 0005 000～20 00020 000～50 000>50 000GB/T 50942-2014,盐渍土地区建筑技术规范[19]地震设防烈度3～44～55～7>7GB 50021-2001,岩土工程勘察规范[13]断层偏压角度/(°)0～1010～2020～30>30断层面倾角/(°)75～9060～7530～60<30隧道距断层距离L/D>21～22/3～10～2/3王鲁南,2012[20];李文华,2013[21]褶皱隧道与褶皱相对位置无褶皱从褶皱两翼穿过与褶皱大角度相交或者与背斜小角度相交与向斜小角度相交董海福,2015[22]地裂缝地裂缝发育程度地面地裂缝不发育或距离拟建工程较远,附近建筑未出现裂缝地面有零星小裂缝且发育不明显,附近建筑有轻微裂缝现象地面地裂缝中等发育,地面有开裂现象,附近建筑有裂缝现象地面地裂缝强发育,附近建筑裂缝明显,可见塌陷坑,路面开裂、隆起地裂缝发展速率0～55～1010～20>20地裂缝埋深/m>2520～2515～200～15隧道距地裂缝距离/m>3015～3010～150～10相交角度/(°)80～9060～8045～600～45杨斌,2017[23]岩爆原始地应力σ0/Rb0～0.150.15～0.250.25～0.35>0.35李继伟,2010[15]

续上表

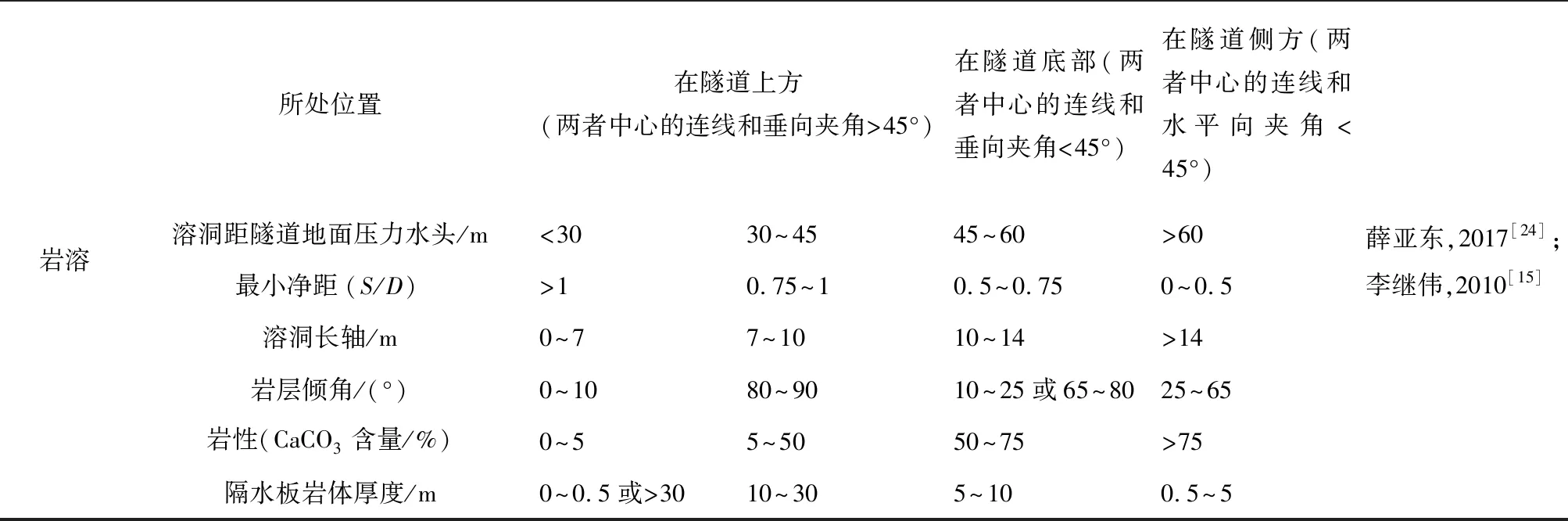
岩溶所处位置在隧道上方(两者中心的连线和垂向夹角>45°)在隧道底部(两者中心的连线和垂向夹角<45°)在隧道侧方(两者中心的连线和水平向夹角<45°)溶洞距隧道地面压力水头/m<3030～4545～60>60最小净距(S/D)>10.75～10.5～0.750～0.5溶洞长轴/m0～77～1010～14>14岩层倾角/(°)0～1080～9010～25或65～8025～65岩性(CaCO3含量/%)0～55～5050～75>75隔水板岩体厚度/m0～0.5或>3010～305～100.5～5薛亚东,2017[24];李继伟,2010[15]

注：① A是指直接临水或强透水层中的地下水；B是指弱透水层中的地下水。强透水层是指碎石土和砂土；弱透水层是指粉土和黏性土。

地铁等轨道交通建设期间发生的工程风险是否可接受和接受程度问题，决定了是否进行风险控制和采取何种措施，因此需要对最终风险评价进行分级。美国《公路和铁路交通隧道检查手册》将隧道的健康等级划分为0到9共十级[25]。我国的风险分级标准包括风险事故发生概率的等级标准和风险事故发生后的损失等级标准，风险发生概率等级和风险事故损失等级都分为五级[26]。王洪林也将轨道交通的风险等级分为5个等级，定量风险指标预警区间为[0,1]，各阈值之间的间隔为0.2，则各风险等级的阈值为0.3、0.5、0.7、0.9[27]。结合前人风险等级的划分方法，考虑到轨道交通隧道不良地质风险等级与风险因素集的风险等级的一致性，将轨道交通隧道的风险等级划分为4个等级，风险指标预警区间为[0,1]，取阈值之间的间隔为0.25，则各风险等级的阈值为0.35、0.6、0.85。本文设立了轨道交通隧道不良地质风险等级表，如表2所示。

表2 轨道交通隧道工程不良地质风险等级表

2 评价指标权重确定

目前权重的确定方法有很多，如专家咨询法、层次分析法、主成分分析法、熵值法和人工神经网络赋权法等。但各赋权法都具有一定的缺陷，例如，专家咨询法有较大的主观经验性，层次分析法的标度问题未得到很好的解决，人工神经网络法需要较多的实测数据支撑。为提高权重的可靠性与客观性，使权重确定方法之间的优缺点得到互补，本文选取了主观的层次分析法和客观的人工神经网络赋权法进行组合赋权;且为了解决层次分析法的标度问题，选取了一种基于层次分析法的乘积标度法。通过相对主观的乘积标度法和客观的BP神经网络赋权对指标赋权，若两种方法的指标权重值差异不大，则表明指标权重合理。

2.1 乘积标度法赋权

国内外较为成功和常用的层次分析标度法有1-9标度法、9/9-9/1标度法、10/10-18/2标度法以及指数标度法。乘积标度法是一种建立在这些方法基础上的赋权法。乘积标度法赋权的步骤是：

1)对n个指标的重要性进行排序；

2)对指标之间进行两两比较，如果A、B两个指标的重要性“相同”，则标度值为A∶B=1∶1，权重为A∶B=0.5∶0.5。如果指标A的重要性比指标B的重要性“稍微大”，由于上面四种标度法对“稍微大”的标度值，分别为3、1.286、1.5和1.277，一般两者之间的差别不应大于1.5，因此指标A、B的标度值为A∶B=(1.286+1.5+1.277)/3∶1=1.354∶1，权重为A∶B=1.354/(1+1.354)∶1/(1+1.354)=0.575∶0.425；

3)如果A、B两个指标的重要性差别很大，一个“稍微大”不足以衡量，则可以认为指标A的重要性比指标B的重要性“稍微大”还“稍微大”，则标度值为A∶B=1.354×1.354∶1=1.833∶1，权重为A∶B=1.833/(1+1.833)∶1/(1+1.833)=0.647∶0.353，以此类推；

4)对该指标层的所有指标进行归一化处理，得到指标层的总权重。

本文对指标之间重要性的判定主要考虑四个方面：① 所选指标是否在相应规范中作为判定标准；② 现场获取指标的可操作性和准确性；③ 对轨道交通隧道工程的危害程度；④ 指标的独立性。

2.1.1 一级指标权重 轨道交通不良地质风险辨识的一级指标层包括11个指标，分别是：围岩等级、复合地层、地下水、有害气体、特殊土、地震、断层、褶皱、地裂缝、岩爆及岩溶。此处一级指标重要性的排序不针对某个地区的轨道交通隧道，而是通过对比不良地质风险源类别对轨道交通隧道工程的影响，进而对一级指标重要性进行排序。对于轨道交通隧道最关注的是围岩等级，围岩等级可以判断围岩的稳定性，判断施工的难易程度，为投资以及结构分析计算提供依据。在地质勘察阶段，最基本的勘察内容包括地层和地下水的信息。隧道工程绝大多数的地质灾害都与地下水的水位、渗漏有着密切关系，而地层则是各种地质因素和隧道工程的承载体。通过对围岩等级、地下水和复合地层的两两比较，认为其重要性“相同”，即围岩等级∶地下水∶复合地层=1∶1∶1。

同理可以对有害气体、特殊土、地震、断层、褶皱、地裂缝、岩爆和岩溶风险源的重要性进行两两比较，继而可以得到一级指标权重值。即围岩等级=地下水=复合地层>岩溶=断层=褶皱>地震>地裂缝=岩爆=特殊土=有害气体，则标度值为(3.360∶3.360∶3.360∶1.833∶1.833∶1.833∶1.354∶1∶1∶1∶1)，将向量归一化，其权重为

ωa=(0.161∶0.161∶0.161∶0.087∶0.087∶ 0.087∶0.065∶0.048∶0.048∶0.048∶0.048)

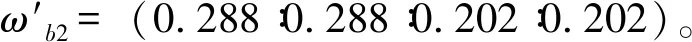
2.2 BP神经网络赋权

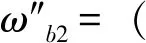
2.3 组合赋权法

(1)

同时，γ和β应满足：

γ+β=1

(2)

由式(1)、(2)可以确定γ和β，进而可以确定组合赋权法的权重ωbi，如式(3)：

(3)

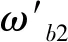
同样的方法可以获得其他各指标的权重。但是由于BP神经网络法赋权需要大量实测数据，实际情况中对于实测数据少的指标，不采用组合赋权，只采用乘积标度法赋权。

3 动态模糊可变评价模型

模糊可变评价模型是基于陈守煜教授的可变模糊集理论[28]的一种可变评价模型，也是目前应用较多的评价模型，结合韩晓军对模糊可变评价模型中参数的研究[29]，建立了针对轨道交通隧道设计、施工阶段地质风险的模糊可变评价模型。传统模糊评价模型的评价级别是一个数值，而模糊可变评价模型将评价级别由一个数值扩展为一个区间范围，使得评价结果更加准确，从而提高了可信度。在模糊可变评价模型的基础上，考虑二级指标的时间因素集，将时间因素加入到模糊可变评价模型，建立了动态模糊可变评价模型，即可实现轨道交通隧道全生命周期的风险等级评价。

3.1 动态模糊可变评价模型的建立

动态模糊可变评价模型的技术路线如图2所示，具体建立方法如下：

BQ=90+3RC+250KV

(4)

式中，KV为岩体完整性系数，RC为岩石单轴饱和抗压强度，其随时间的变化规律(以花岗石为例)如式(5)所示[30]。

RC=224.5exp(-0.071lnt)

(5)

复合地层随时间变化的辨识因子包括黏聚力c和內摩擦角φ，其随时间的变化规律(以高庙子膨润土为例)如式(6)、式(7)所示[31]。

c=907.7exp(-0.030 8t)+664.4exp(0.005 247t)

(6)

φ=4.365exp(-0.134 6t)+11.23exp(-0.000 916 6t)

(7)

2)确定i个指标h个级别的吸引区间[a,b]的矩阵Iab。Iab即[a,b]ih表示i指标h级别的风险因素集评判标准区间。

(8)

式中，h=1,2,…,n，n为评价等级上限。

3)由确定的各指标的吸引域区间[a,b]，确定对应的范围值区间[c,d]，[c,d]表示指标的风险因素集评判标准区间[a,b]的扩展区间，进而构造i个指标h个级别的范围值矩阵Icd。范围值区间[c,d]的确认可以按照式(9)。

(9)

式中，ha为a所处的级别；hb为b所处的级别。则，

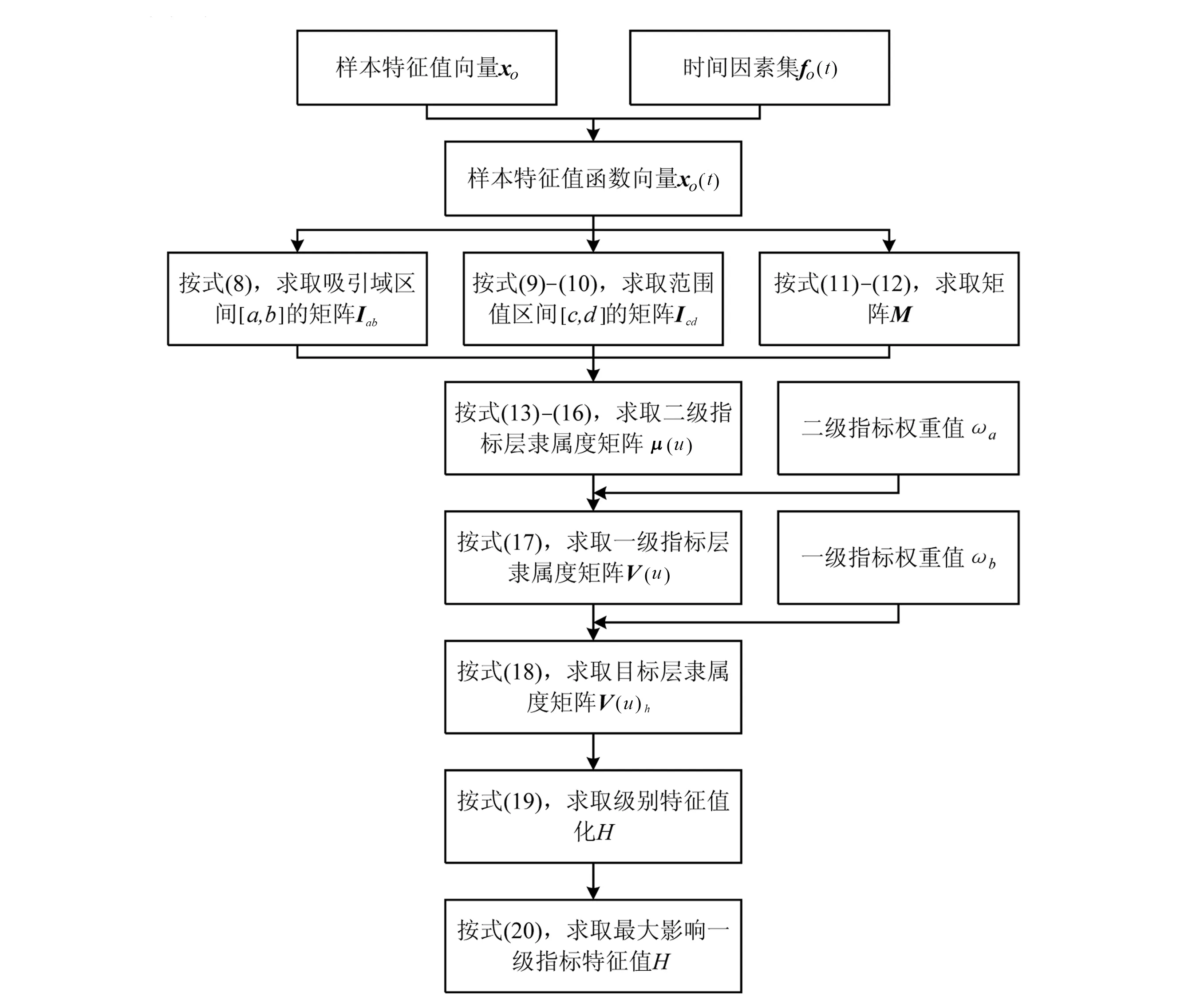
图2 动态模糊可变评价模型技术路线图

(10)

式中，h=1,2,…,n，n为评价等级上限；[c,d]ih表示i指标h级别的风险因素集评判标准区间[a,b]ih的扩展区间。

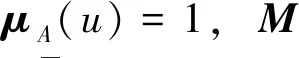
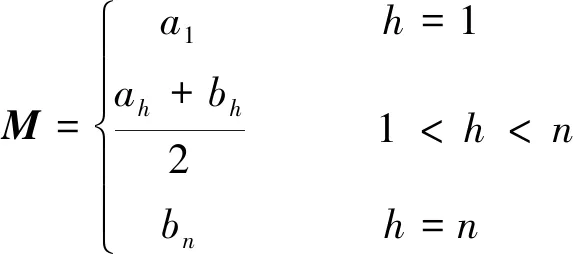
(11)

式中，h=1,2,…,n，n为风险等级上限。则：

(12)

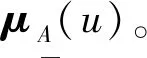
①当xo(t)落在M点左侧时，相对差异函数模型为：

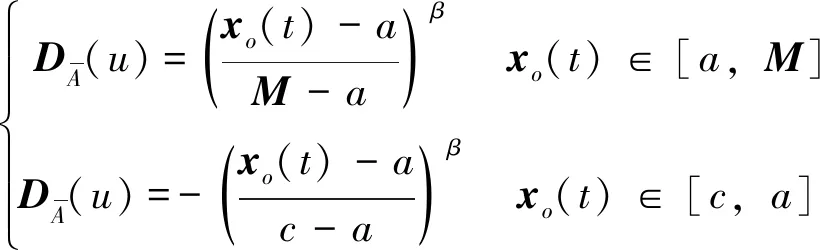
(13)

②当xo(t)落在M点右侧时，相对差异函数模型为：

(14)

经过求取相对差异函数DA(u)，就可以求取相对隶属度，则:

(15)

(16)

6)确定指标权向量。由评价指标确认部分确定一级指标和二级指标的权向量ωa和ωbi。

(17)

式中：α为模型优化准则参数，α=1时为最小一乘方准则，α=2时为最小二乘法准则；p为距离参数，p=1时为海明距离，p=2时为欧式距离；m为识别指标数；ωbi为二级指标的第i个指标权向量。当α=1，p=1时，此时模型是简单模糊评价模型；当α=1，p=2时，此时模型是理想点评价模型；当α=2，p=1时，此时模型是“S”型函数模型；当α=2，p=2时，此时模型是模糊优选模型。

(18)

8)根据表2得到级别特征值公式(19)，分别求得4种模型的级别特征值，进而根据表2评价轨道交通隧道工程的地质风险等级。则：

(19)

3.2 模型检验

以广州某拟建轨道交通线路几个区段的地质数据检验模型的可靠性，主要包括围岩等级、复合地层、地下水、地震、断层和岩溶6个风险源的数据，如表3所示。

表3 初步勘察阶段的地质数据表

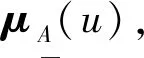
表4 轨道交通各区段的地质风险等级

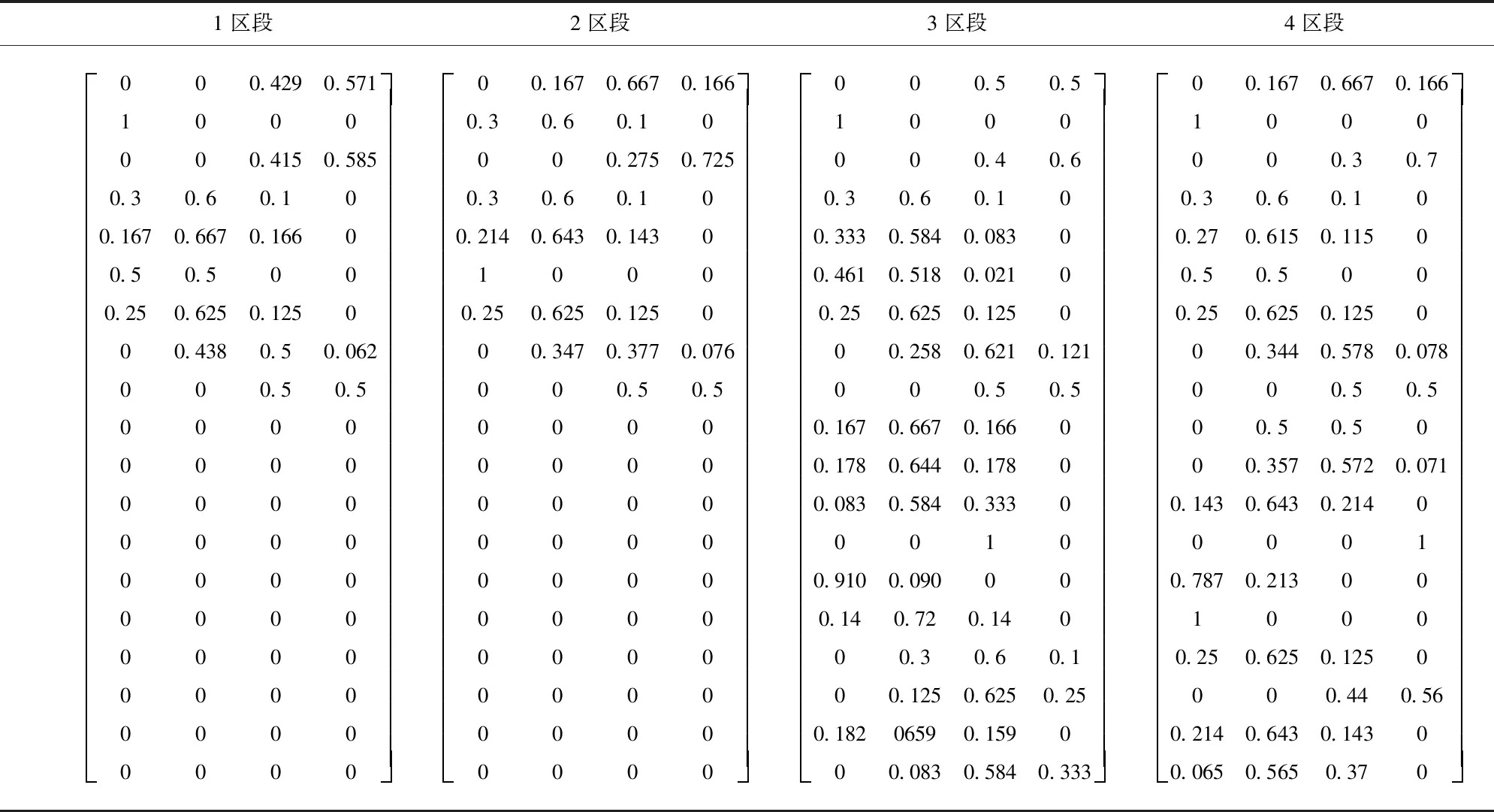
表5 广州某拟建轨道交通线路各区段的隶属度矩阵

由表4可以得出，区段1和区段3的特征值分别在0.537～0.574、0.568～0.598的范围，拟建隧道工程该区段的地质风险等级是Ⅲ级(中风险)；在轨道交通隧道工程施工过程中，需要对该区段的地质风险源进行合理的处理，以提高隧道安全性；区段2的特征值范围在0.578～0.626，均值在Ⅲ级(中风险)特征值的下限值0.6，一旦隧道工程地质环境在施工阶段发生恶化，区段2将会处于Ⅲ(中风险)等级，因此在施工阶段需要对该区段进行地质环境的改善；区段4的特征值范围为0.586～0.655，虽然该段地质风险等级为Ⅱ级(弱风险)，但其特征值最大值接近于Ⅲ级(中风险)特征值的下限值0.6，最小值已经小于0.6，说明该段部分不良地质风险源已经处于Ⅲ级(中风险)。综上可知，该拟建轨道交通隧道工程大部分地质环境处于Ⅲ级(中风险)。模型的评价结果与现场实测和调查结果相符，验证了本模型的可行性。

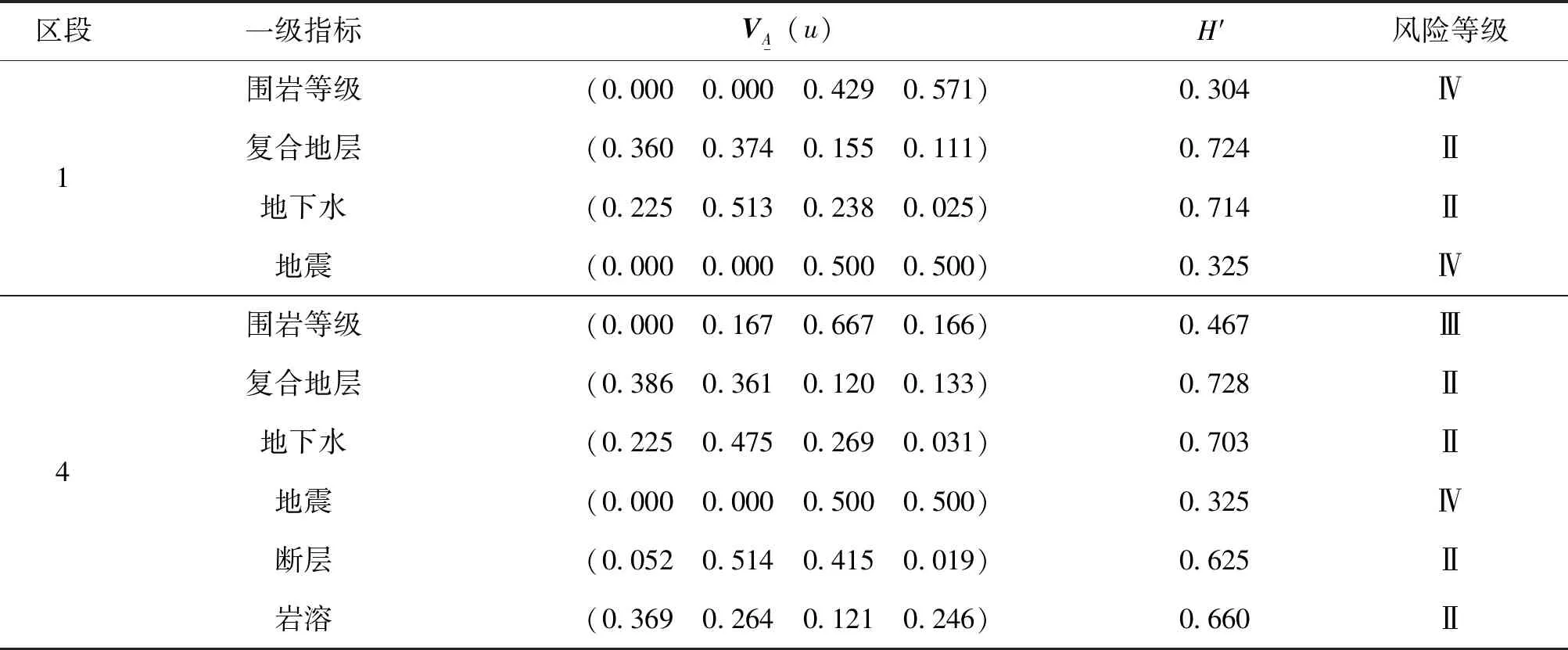
(20)

由表6可知，影响轨道交通隧道区段1风险等级的最大因素为围岩等级，特征值H′为0.304，属于强风险(Ⅳ级)；影响轨道交通隧道工程区段4风险等级的最大因素为地震，特征值H′为0.325，属于强风险(Ⅳ级)；而断层和岩溶的特征值H′分别为0.625和0.660，属于弱风险(Ⅱ级)。因此区段1在隧道施工过程中应重点针对围岩等级进行处理，同时也应关注隧道的抗震性能，而在区段4应着重考虑隧道的抗震性能。

4 结 论

通过以上的研究分析，得到如下主要结论：

(1)基于“定量为主，定性与定量相结合”的原则，确立了轨道交通隧道11个一级地质风险源及40个二级风险辨识因子，并且总结出了各指标风险等级判定标准，将风险等级分为微风险、弱风险、中风险和强风险四级。

(2)采用BP神经网络和乘积标度法对指标层进行组合赋权。基于可变模糊集理论，建立了针对轨道交通隧道设计、施工阶段的模糊可变评价模型; 通过模型参数的变化，将评价级别由一个数值扩展为一个区间范围，使得评价结果更加准确。

(3)将时间因素集加入模糊可变评价模型，实现了隧道工程某些地质风险的动态评估。加入轨道交通隧道运维期的风险因素集，即可实现轨道交通隧道全生命周期的风险等级评价。利用广州某拟建轨道交通的初步勘察地质数据对模型进行了检验。模型结果与现场实测和调查结果相符，证明本文的轨道交通隧道的动态模糊可变评价模型是合理的、可靠的。