载重车中央充放气系统自动控制算法研究*
胥军,苏田,李刚炎,程毅
(武汉理工大学机电工程学院,湖北 武汉 430070)
近年来,轮胎压力监测系统已经成为国际公认的汽车三大安全系统之一,轮胎中央充放气系统是在轮胎压力监测系统 (tire pressure monitoring system,TPMS)的基础上发展而来的,用于在车辆行驶过程中保持合适的胎压,一方面可减少车辆的燃油消耗与轮胎磨损,另一方面可以大幅提升车辆的行驶安全性。电控式轮胎中央充放气系统通过实时获取胎压,以当前气压值与目标值的偏差为依据,实时计算轮胎充气或放气所需的时间,控制电磁阀动作,通过轮边装置对相应的轮胎进行充气或放气操作。随着旋转气动密封和汽车电子控制技术的不断成熟[1-4],电控式轮胎中央充放气系统的综合应用成本不断降低,其逐步从军用运输车辆拓展到各型民用运输车辆中。
2018年,我国的商用车总销量突破了358万辆,重型运输车的占比达到33.4%[5],其中用于公路物流运输的载重车的销量得到了大幅提升。载重车因其质心高、承载量大,在行驶过程中若出现胎压不平衡,极易发生侧倾、侧翻、爆胎,由此导致严重的安全事故。据统计,在我国高速公路上发生的各类交通事故中,约45% 是由轮胎故障引发的,其中胎压不平衡是主要诱因之一。SAE的统计结果也表明,美国每年约有26万起的交通事故和75% 的轮胎故障是由胎压异常和轮胎渗漏造成的[6]。为保障载重车的行驶安全,轮胎中央充放气系统及其控制技术日益受到关注。为实现电控式轮胎中央充放气系统的精准控制,本文在充分考虑充放气过程中动压对胎压变化的基础上,以某型6×4载重车为例,提出了一种模糊-补偿式控制算法,经联合仿真与实测验证,该算法能够通过欠压自动补偿、过压自动调节实现胎压实时调节,且故障响应时间优于GB/T 26149-2010的要求。
1 中央充放气系统的特性
1.1 中央充放气系统的结构
中央充放气系统前桥的简化模型如图1所示。空压机产生压缩气体进入储气罐达到稳压状态后,气体通过气源电磁阀、轮胎充气电磁阀和轮边装置进入轮胎,对轮胎充气;当轮胎需要放气时,轮胎内的气体直接通过轮边装置和轮胎放气电磁阀排放到大气。轮边装置用于将固定的气体管路与旋转的轮胎气门连接。
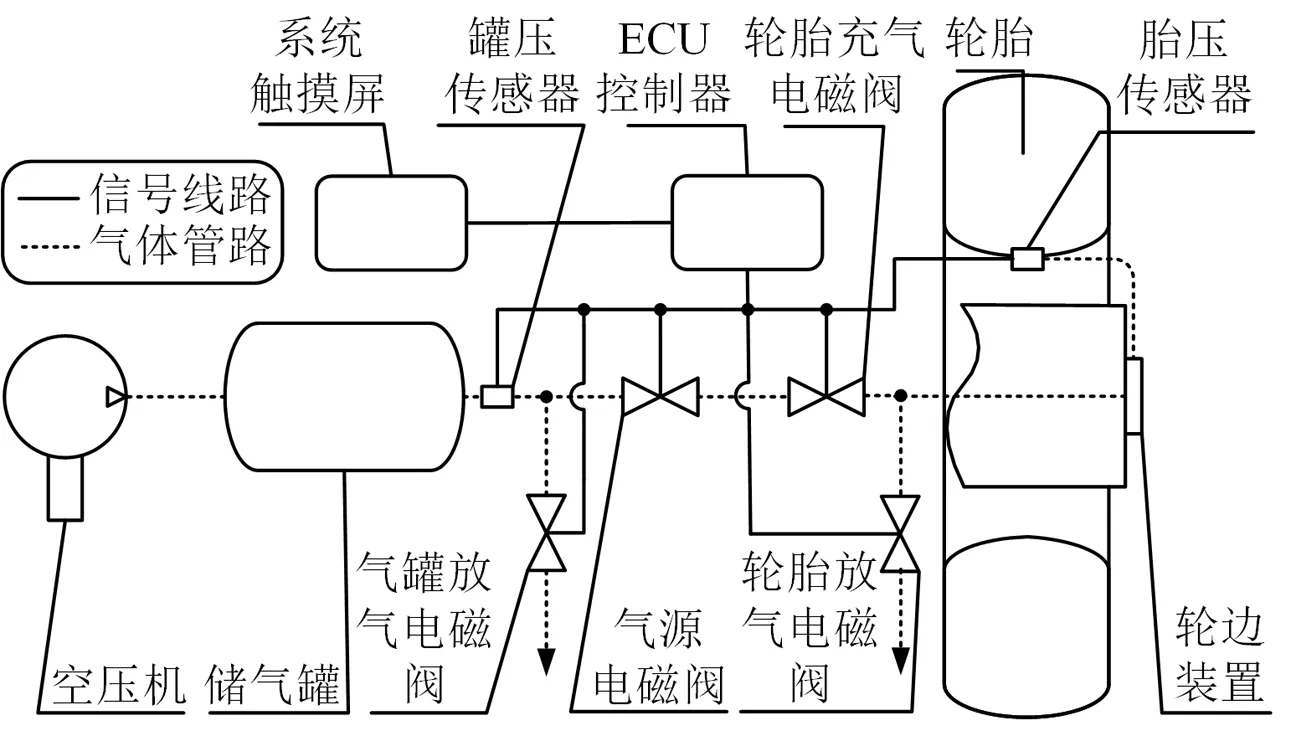
图1 中央充放气系统前桥的简化模型
1.2 充放气过程中胎压的特性
在轮胎充放气过程中,由于空压机产生的压缩气体已在储气罐内达到稳压状态,可将轮胎充气电磁阀之前的装置视作稳压气源,仅考虑轮胎充气电磁阀与轮胎之间的管路,管路的流通能力取决于该段管路的有效截面积,放气管路采用相同的处理方法。轮胎充放气过程的简化模型如图2所示,该模型主要由气源、节流孔、轮胎组成。
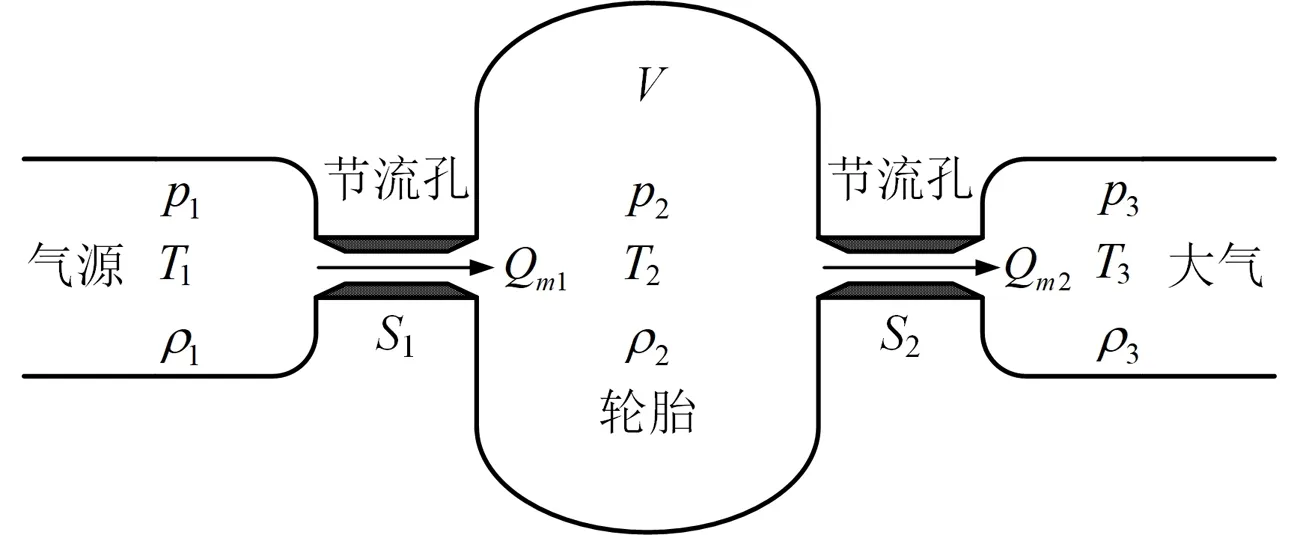
图2 充放气管路简化模型
将轮胎充放气视为等温充放气过程,当p2/p1≤b时,节流孔内气体流动属于音速流动,由p20充气至p2所需时间t如式(1)所示。
(1)
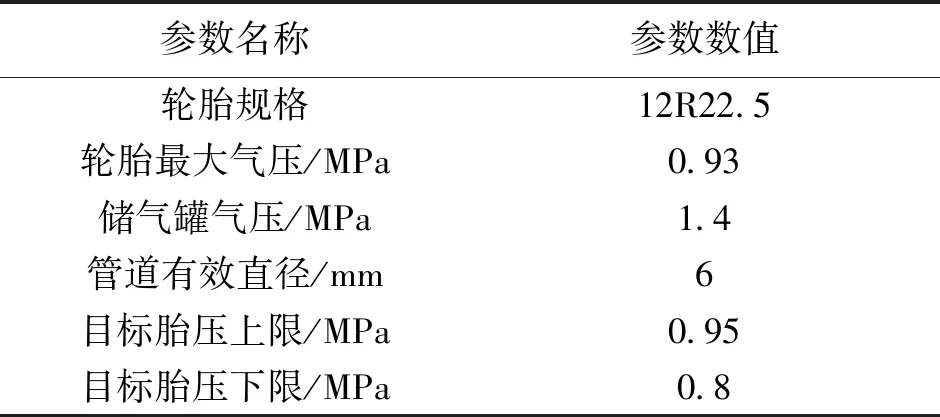
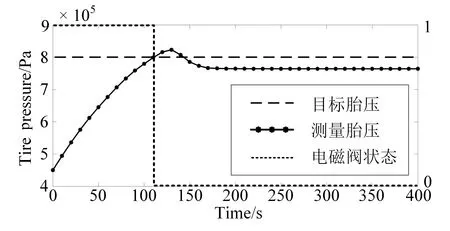
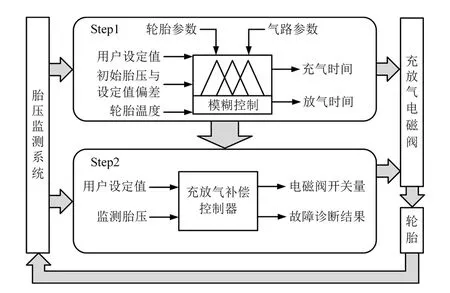
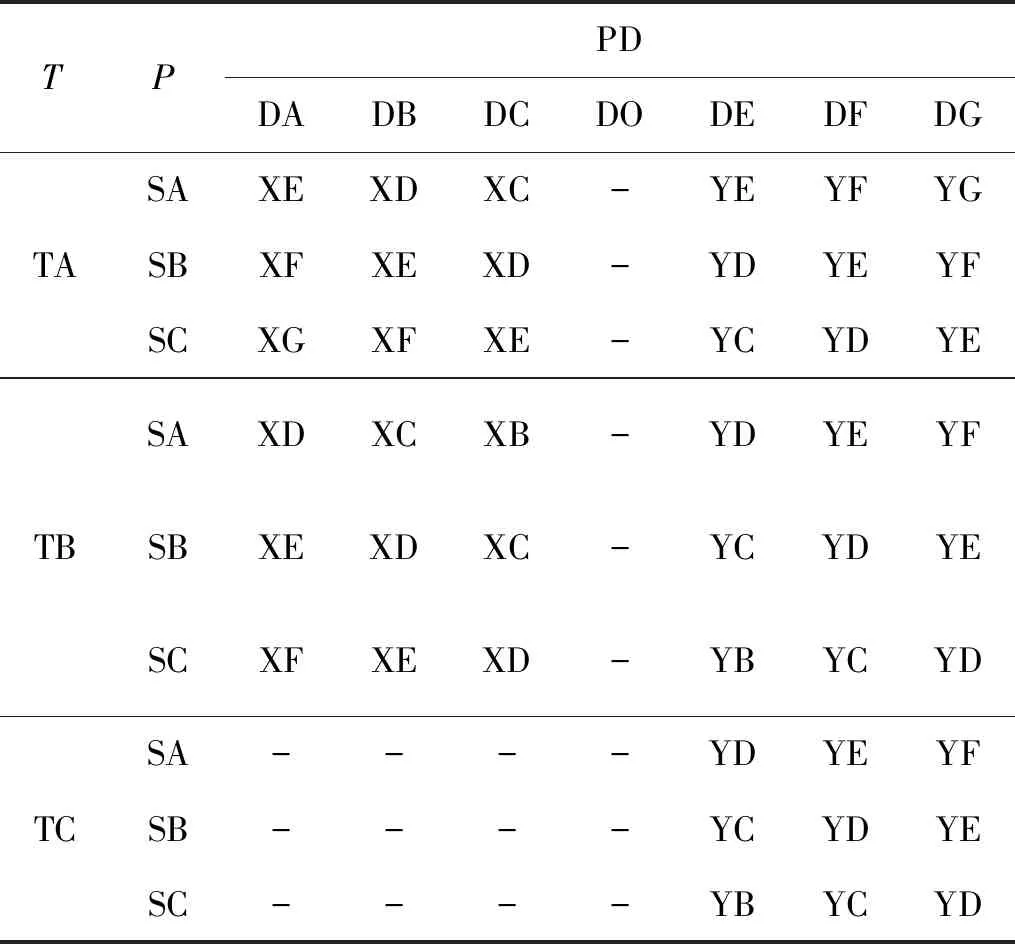
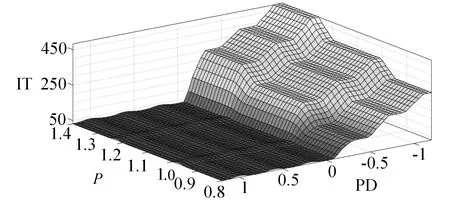
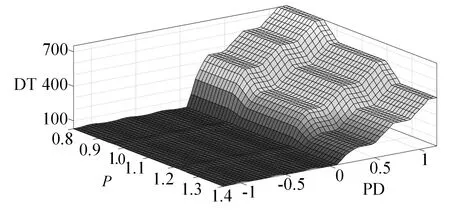
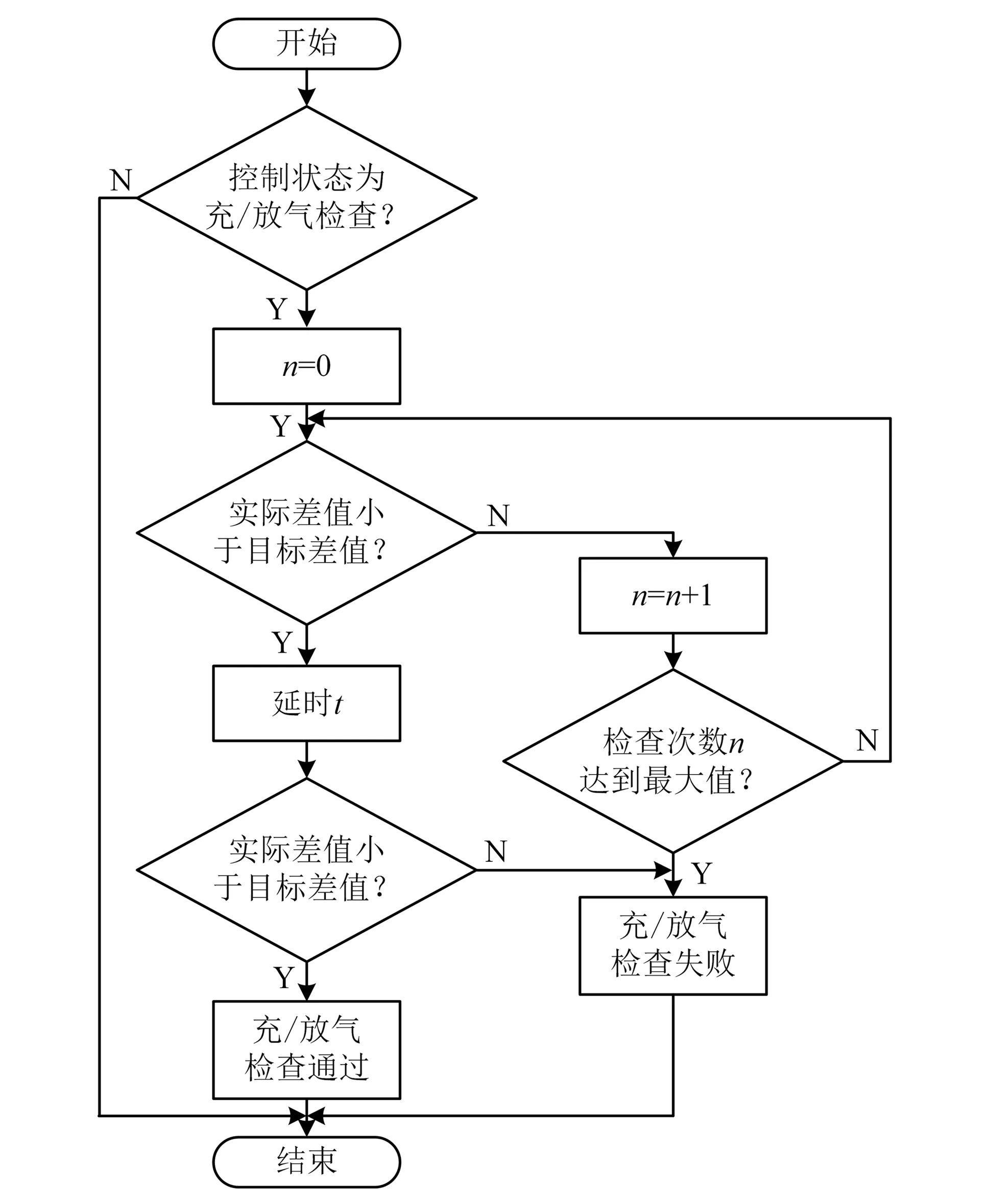
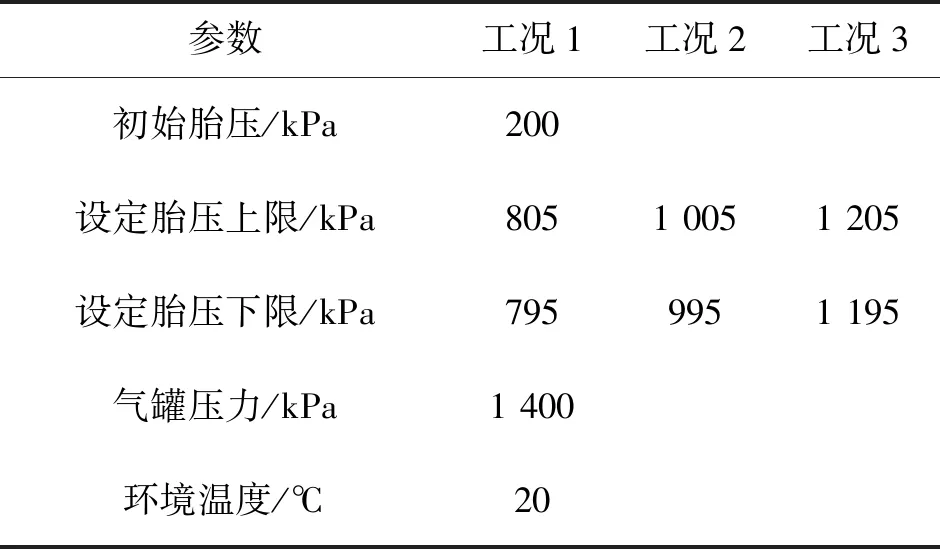
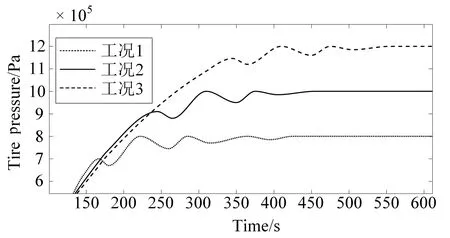
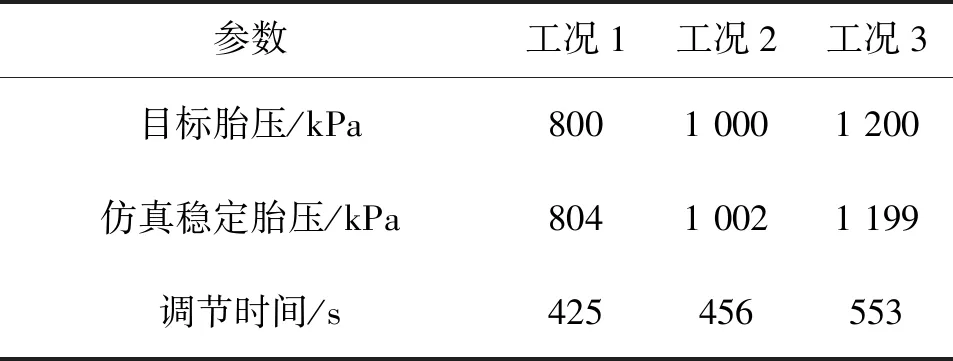
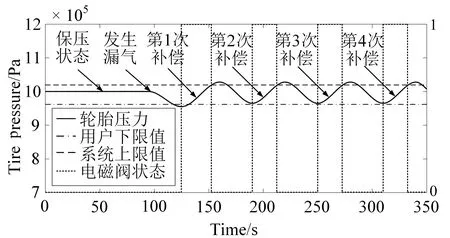
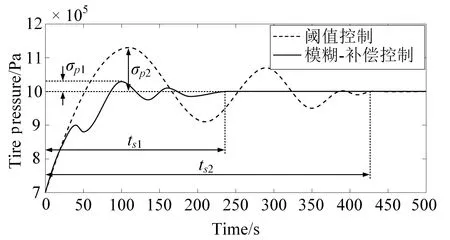
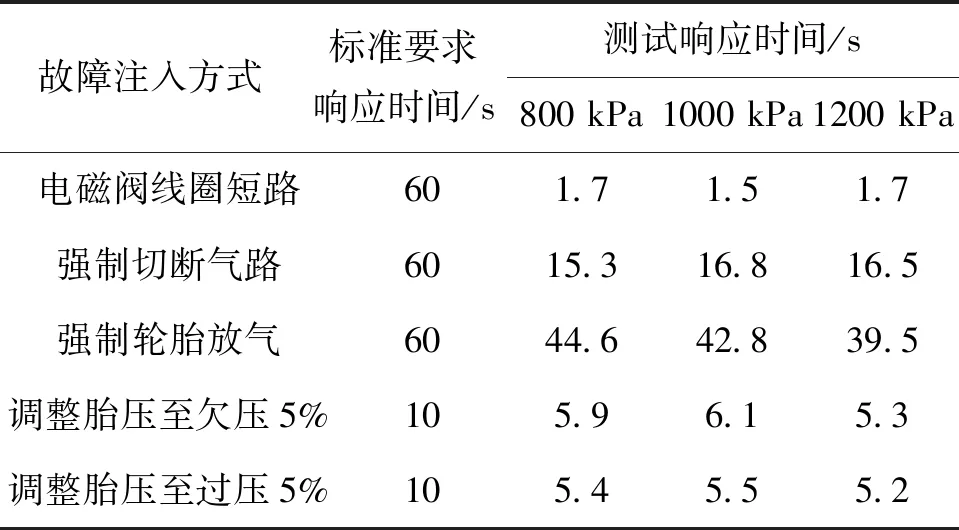
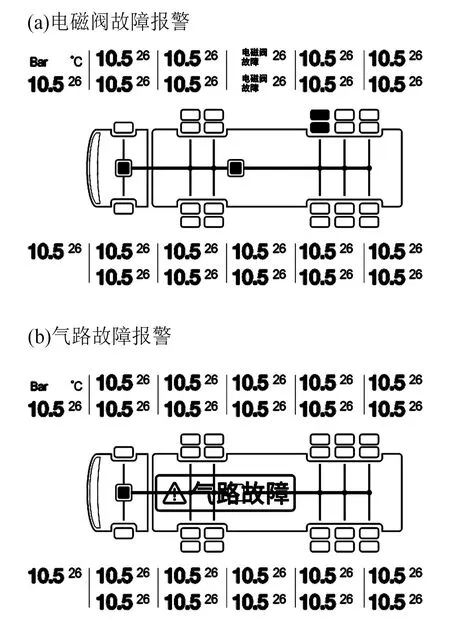
当b (2) 其中,V为轮胎容腔体积,m3;p1为上游气体压力,Pa;p2为下游气体压力,Pa;R为气体状态常数,J/(kg·K);S为管道有效横截面积,m2;T1为环境温度,K;b为临界压力比。 以某型6×4载重车为例,其参数如表1所示。 表1 目标车辆工况参数 在气源压力为1.4 MPa的情况下,对轮胎充气至0.8 MPa后关闭电磁阀,试验过程中胎压变化如图3所示。 图3 充气试验的胎压变化曲线 试验结果表明,在充气过程中气体动压会对胎压传感器压力测量值产生较大影响,进而会导致胎压实际值与设定值产生偏差,即充气不足。已有的轮胎中央充放气系统多采用胎压差值计算或模糊推理充放气时间方式的控制算法[7-8],上述算法通过计算实际胎压值与设定值的差值,然后依据差值的大小计算出充气或放气所需时间。由于在轮胎充放气过程中,轮胎充放气时间会受到空压机性能指标、气体管路有效截面积、轮胎温度、轮胎变形等多方面因素影响,传统控制方式会使胎压数值严重偏离用户设定值。 为补偿充放气过程中的胎压测量值与充放气动作结束后的胎压测量值间的误差,实现胎压的精确快速控制,本文提出一种轮胎充放气模糊-补偿控制算法,该算法主流程由两阶段组成,分别为模糊快速充放气阶段、充放气补偿与状态诊断阶段。该控制算法的控制主流程如图4所示。 第一阶段,该算法将用户设定值、初始胎压与设定值偏差、轮胎温度作为模糊控制器的输入,利用轮胎与中央充放气系统参数建立模糊控制规则,最终通过模糊控制运算得出充放气时间,使轮胎快速充放气至用户设定值附近;第二阶段,利用胎压监测系统所反馈的轮胎状态参数控制电磁阀进行充放气补偿,并通过控制器诊断轮胎与中央充放气系统故障。 图4 充放气自动控制算法主流程 在模糊快速充放气阶段,系统根据当前实际胎压值与用户设定值P计算出初始胎压与设定值偏差PD。由于轮胎在不同压力范围下的充放气速率各不相同,必须同时考虑用户设定值P和初始胎压与设定值偏差PD才能得到较为准确的充放气时间。为进一步提高中央充放气系统的安全性,可将轮胎温度T作为系统参考,在温度异常时对轮胎采取相应措施以保证轮胎安全。 综上所述,将模糊控制器的输入设为用户设定值P、初始胎压与设定值偏差PD、轮胎温度T,输出为充气时间IT或放气时间DT。 P的模糊子集为{SA(低压)、SB(中压)、SC(高压)},论域为[0.8,1.4];PD的模糊子集为{DA(负大)、DB(负中)、DC(负小)、DO(零)、DE(正小)、DF(正中)、DG(正大)},论域为[-1.2,1.2];T的模糊子集为{TA(低温)、TB(中温)、TC(高温)},论域为[-20,130];IT的模糊子集为{XA(超短)、XB(很短)、XC(较短)、XD(中等)、XE(较长)、XF(很长)、XG(超长)},论域为[0,600];DT的模糊子集为{YA(超短)、YB(很短)、YC(较短)、YD(中等)、YE(较长)、YF(很长)、YG(超长)},论域为[0,900]。 工程中常用的隶属度函数有三角形隶属度函数、梯形隶属度函数、通用贝尔隶属度函数、高斯隶属度函数等[9]。经过试验研究表明,三角形隶属度函数灵敏度较高,梯形隶属度函数稳定性较好。为提高控制算法的综合性能,用户设定值和轮胎温度选择梯形隶属度函数,胎压与设定值偏差和充放气时间选择三角形隶属度函数。 模糊规则库是系统进行模糊推理的重要基础,根据Mamdani模糊推理方法,对应三维模糊控制器建立“if…and…and…then…”形式的模糊推理语句,所建立的三维模糊规则如表2所示。 表2 模糊控制规则 在完成模糊推理后,需要将模糊推理结果进行解模糊化得到确切的充放气时间结果,本系统选用重心法(centroid)为解模糊化方法,IT与DT解模糊化公式如式(3)-(4)所示,IT与DT解模糊化曲面如图5-6所示。 (3) (4) 图5 IT解模糊化曲面 图6 DT解模糊化曲面 为补偿放气过程中的胎压测量值与充放气动作结束后的胎压测量值间的误差,实现胎压的精确控制,本文提出一种轮胎充放气补偿算法以实现胎压控制的精确化,该算法首先依据用户设定的胎压上限值Pmax和胎压下限值Pmin,生成由系统上限值Cmax和系统下限值Cmin构成的阈值区间,Cmax和Cmin的计算方法如式(5)所示。通过实时调节,使胎压始终处于阈值区间内。 (5) 式中,k1和k2满足1 >k1>k2> 0。 充放气补偿算法采取多次短时充放动作直至胎压达到用户设定值,在多次短时充放动作中胎压传感器会实时监测轮胎压力,当达到系统上限值会立即停止充放气,充放气检查是测量稳定胎压是否达到用户设定值的重要步骤,传统的充放气检查算法采用单次测量[10],即在充放气动作结束之后,测量某一时刻的胎压且仅测量一次。但在实际工况中,即使充放气动作结束,轮胎的胎压也不是绝对稳定不变,还可能有其他因素引起胎压波动,例如轮胎漏气、外部冲击、机械振动等。为解决上述问题,提出一种充放气检查算法,该检查算法的检查流程如图7所示。 图7 充放气检查算法流程 当实际控制状态为充(放)气检查时,系统首先应检查实际差值是否小于目标差值(实际差值计算如式(6)所示,目标差值由用户根据实际要求自行设定),当实际差值小于目标差值时,系统会延时一段时间t,然后再次检查实际差值是否小于目标差值,若再次检查仍小于目标差值,则充(放)气检查通过。在系统首次检查实际差值时为防止胎压波动造成检测失误,会设置一个检查次数最大值,如果首次检查失败,系统会再次进行检查,直至检查的实际差值小于目标值或检查次数n达到最大值,根据单位周期内充放气检查失败次数的结果可诊断充放气系统或轮胎故障。 ΔP=|PT-(Pmax+Pmin)/2| (6) 其中,ΔP为实际差值;PT为检测胎压。 由于中央充放气系统的管路及性能限制,在轮胎有充气作业请求时,在同一时刻仅允许一个轮胎进行充气动作,放气作业请求则无限制。为此,本文采用先到先服务的调度算法。 采用AMESim与MATLAB搭建联合仿真平台,根据上文所述的控制算法,采用Simulink/Stateflow搭建充放气控制模型,利用AMESim内部的Pneumatic、Signal、Control库等模型库搭建模拟实际工况的管路、电磁阀、轮胎模型。基于联合仿真平台,对充放气控制算法进行验证,验证过程如图8所示。 图8 联合仿真验证过程 为验证本控制算法在多种胎压等级工况下的适应性,分别设置三种不同胎压等级工况,即工况1、工况2、工况3。三种仿真工况的参数设置如表3所示。 表3 仿真工况参数设置 以时间为自变量,按0.01 s为步长控制AMESim模型中轮胎压力达到设定范围内,并记录轮胎压力随时间的变化。三种工况下的胎压曲线如图9所示。 图9 充气仿真过程中的胎压变化 由图9可以得出三种工况下的调节时间和仿真稳定胎压,具体结果如表4所示。 表4 仿真结果 仿真结果表明,该控制算法会根据胎压波动做出一次或多次调节,最终稳定胎压均符合目标胎压要求。为验证控制算法的故障报警功能,设定一种模拟的轮胎漏气故障工况:轮胎初始胎压为1 000 kPa,在初始阶段为保压状态,随后模拟发生漏气,仿真的胎压曲线如图10所示。 图10 漏气故障工况胎压变化 由图10可知,在发生漏气后,胎压传感器在约125 s时检测到胎压值低于用户下限值,控制系统开始进行充气动作,由于漏气原因此时轮胎的充气速率会低于正常情况下的充气速率;在约150 s时胎压传感器检测到充气瞬时气压高于系统上限值,控制系统停止充气动作开始进行充气检查,由于漏气原因在充气检查过程中胎压无法达到稳态平衡;在约185 s时系统判断充气检查失败,控制系统开始继续充气;在约215 s时充气瞬时气压再次高于系统上限值,但是由于漏气故障未修复,在后续阶段系统会再次判断充气检查失败。如漏气故障一直未修复,后续系统将一直进行此循环动作,这时系统自计的打破平衡次数也会不断累加,当打破平衡次数高于某设定值时,系统会发出轮胎漏气报警。 由于AMESim-MATLAB联合仿真忽略了系统硬件因素对中央充放气系统性能的影响,为提高控制模型的置信度,搭建适用于中央充放气系统控制算法验证的硬件在环测试平台,如图11所示。 图11 中央充放气控制硬件在环测试平台 中央充放气系统控制器硬件在环测试平台主要由三部分构成:车辆模型仿真平台、轮胎及管路仿真平台、参数注入及状态反馈平台。通过TruckMaker搭建车辆动力学模型,并利用Xpack4组件的M410模块将轮速数据以CAN总线的传输方式传递给中央充放气系统控制器。由于TruckMaker所提供的车辆模型缺少轮胎气压模型,为提高硬件在环测试的完整性,利用dSPACE实时仿真系统搭建了轮胎及管路仿真平台,将TruckMaker所提供的轮胎负载数据通过CAN总线传递给dSPACE,以供dSPACE内部的轮胎充放气及管路模型参考。为实时监控控制器的运行状况和输入相关工况参数,利用Vehicle Spy3汽车总线仿真测试平台搭建参数注入和状态反馈平台。 置初始轮胎压力为200 kPa,目标胎压区间为995~1 005 kPa,分别启动阈值控制和模糊-补偿控制进行充气,整理试验记录得到轮胎压力变化的对比曲线,如图12所示。 图12 对比试验过程中胎压变化 由图12可见,模糊-补偿控制的胎压曲线超调量σp1明显小于阈值控制的超调量σp2,较小的超调量可提高充放气过程中的安全性,同时模糊-补偿控制的胎压曲线调节时间ts1明显小于阈值控制的调节时间ts2,较小的调节时间可提高充放气的效率。 试验期间内,为测试控制系统的诊断功能和响应时间,按照GB/T 26149-2010和SAE J2848-3-2012标准采取表5所示的五种注入故障的方式,在三种胎压设定工况下分别模拟电磁阀故障、气路故障、轮胎漏气、轮胎欠压、轮胎过压,系统测试记录如表5所示。 表5 模拟故障注入试验测试数据 监测界面可实时显示中央充放气自动控制系统的运行状态,显示的主要信息包括轮胎气压、轮胎温度、各动作指示及系统报警情况等,其中电磁阀故障报警与气路故障报警提示界面分别如图13中(a)、(b)所示。 应用本文充放气自动控制算法的控制器原型已安装在东风特专生产的某型载重车上进行了实车测试,如图14所示。设置路面信息后,启动车辆点火开关,利用控制系统触摸屏设置相关参数,设置完成后重启系统开始功能验证。测试结果与硬件在环试验结果一致,验证了该控制算法的胎压调节效果。 图13 故障提示界面 图14 装车对比验证 本文针对载重车辆,采用理论分析、联合仿真与试验验证相结合的方法,提出了一种中央充放气系统的自动控制算法。通过分析轮胎充放气过程中的胎压特性建立了充放气模型;以此为基础设计了中央充放气系统的控制算法,并基于AMESim-MATLAB联合仿真平台证明了该控制算法的有效性;通过硬件在环试验和装车测试进行了控制效果验证,与现有的胎压差值计算时间方式相比,胎压调节响应速度快、精度高且故障诊断快速,为载重车中央充放气系统控制器的开发提供了依据。由于缺乏对实际路面及车辆工况的主动识别研究,未能深入考虑人—车—路之间的信息交互,将来可考虑通过滑移率等车辆状态信息自动识别路面工况,实现系统智能决策,进一步提高系统操作的简便性与可靠性。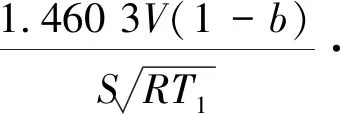
2 充放气自动控制算法设计
2.1 充放气自动控制算法主流程设计
2.2 模糊快速充放气算法设计
2.3 充放气补偿与状态诊断算法设计
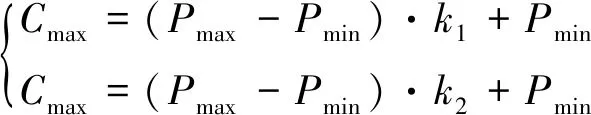
3 AMESim-MATLAB联合仿真
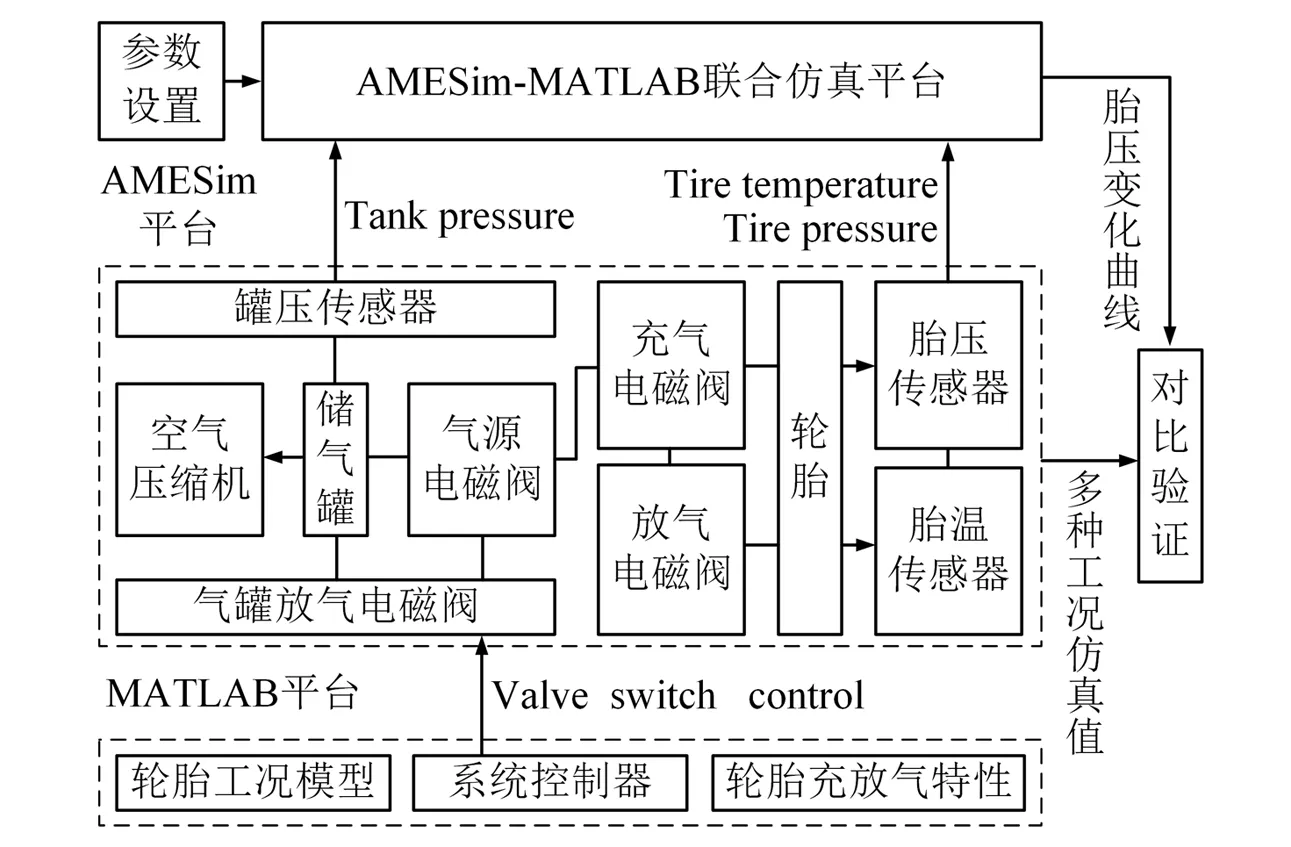
3.1 联合仿真平台的搭建
3.2 参数及工况设置
3.3 仿真结果分析
4 充放气控制算法验证
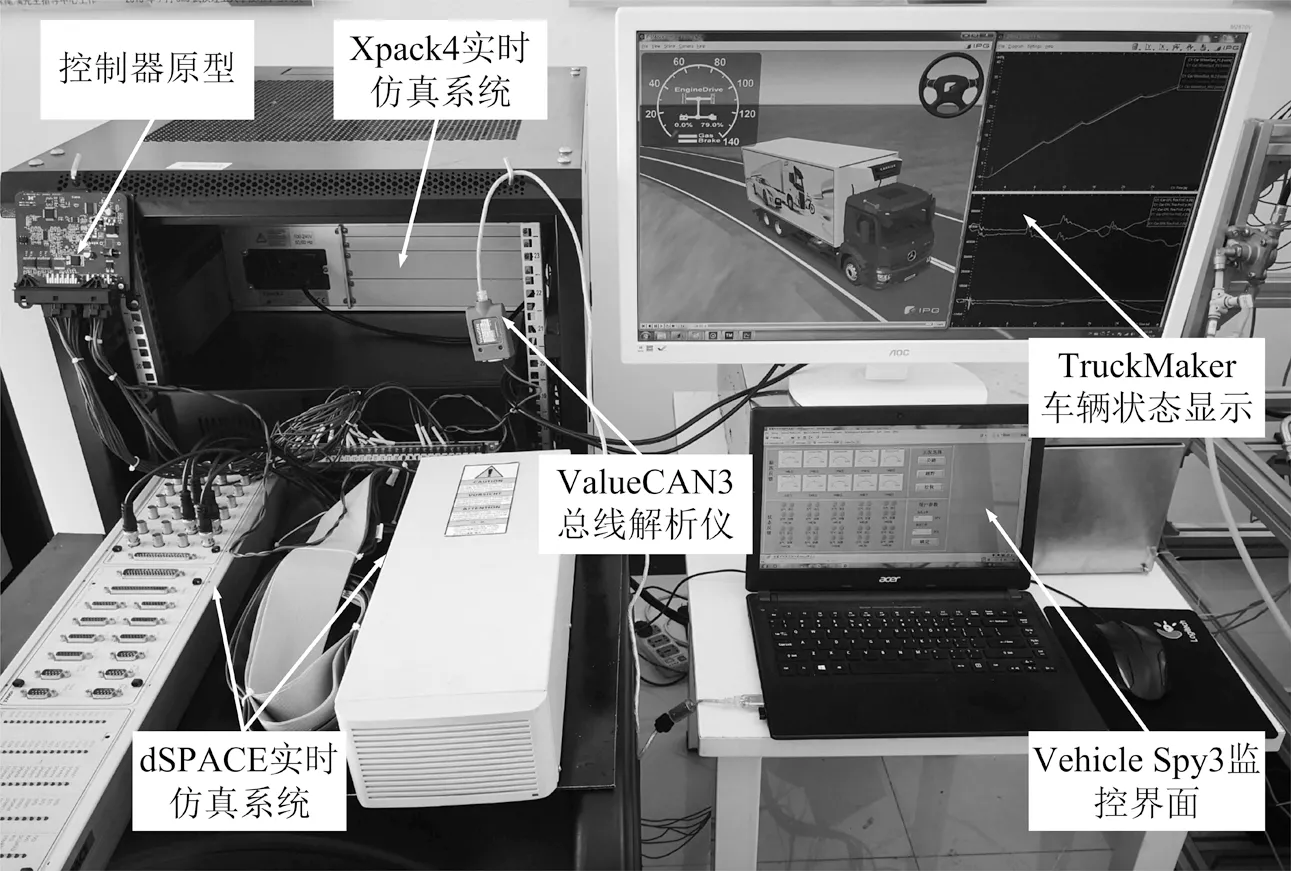
4.1 硬件在环测试平台的建立
4.2 控制算法试验验证

5 结 论
——元征X-431标定胎压传感器的方法

