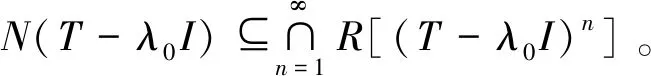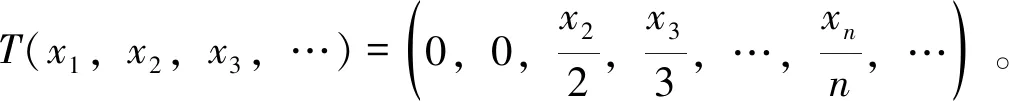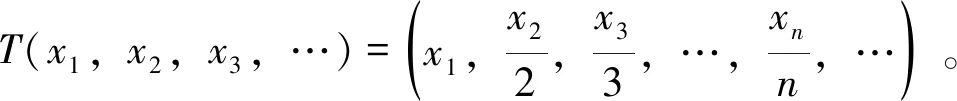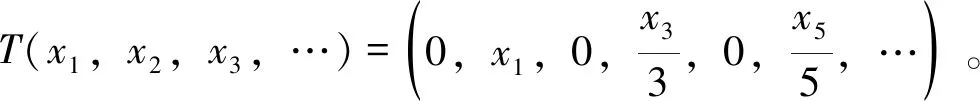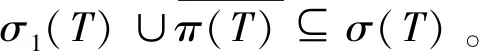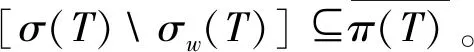有界线性算子及其函数演算的Weyl定理*

闫慧凰，曹小红

( 1. 长治学院数学系，山西 长治 046011；2. 陕西师范大学数学与信息科学学院，陕西 西安 710119)

在算子理论的研究中，谱理论的研究一直是一个深受学者们关注的热点问题，而探索算子的Weyl定理对算子谱理论的研究有着重要的意义。1909年，Weyl发现了自伴算子T的所有紧摄动的谱集的交集恰好等于T的谱集但不为T的谱集中的孤立的有限重特征值。之后，这一结论被人们称为Weyl定理。Weyl定理的研究从发现以来一直备受学者们的广泛关注，许多学者对 Weyl定理进行了变形并且将Weyl定理扩展到Hilbert空间和Banach空间上的各类算子中去。例如Coburn[1]和Berberian[2]研究了非正规算子的Weyl定理；Raul[3]研究了Algebraically Paranormal算子的Weyl定理。甚至学者们将Weyl定理的研究扩展到算子矩阵中[4]。本文通过新定义的谱集刻画了有界线性算子及其函数演算的Weyl定理的等价条件。另外，探索了p-hyponormal(或M-hyponormal)算子及其函数演算的Weyl定理。

1 预备知识

在本文中，H表示为复可分的无限维的Hilbert空间，B(H)表示为H上有界线性算子的全体。令T∈B(H)，那么T的零度n(T)为T的零空间N(T)的维数，T的亏数d(T)为T的值域R(T)的余维数。若n(T)<∞且R(T)是闭集，那么称T为上半Fredholm算子；若T为上半Fredholm算子且d(T)<∞，则称T为Fredholm算子。特别地，当T为Fredholm算子且n(T)=d(T)=0时，那么称T为可逆算子。再者，若T为指标ind(T)=n(T)-d(T)=0的Fredholm算子，那么称T为Weyl算子。我们定义算子T的升标

asc(T)=inf{n∈N:N(Tn)=N(Tn+1)}

和降标

des(T)=inf{n∈N:R(Tn)=R(Tn+1)}

若T的升标和降标有限，则称T为Drazin可逆算子。若T为Fredholm算子并且是Drazin可逆的，则称T为Browder算子。众所周知，T为Browder 算子当且仅当T为Weyl算子且T的升标或降标有限。显然，Browder算子一定是Drazin可逆算子。下面，我们分别定义算子T的谱σ(T)，上半Fredholm谱σSF+(T)，本质谱σe(T)，Weyl谱σw(T)，Browder谱σb(T)和Drazin谱σD(T)如下：

σ(T)={λ∈C:T-λI不是可逆算子}，σSF+(T)={λ∈C:T-λI不是上半Fredholm算子}，

σe(T)={λ∈C:T-λI不是 Fredholm算子}，σw(T)={λ∈C:T-λI不是Weyl算子}，

σb(T)={λ∈C:T-λI不是 Browder算子}，σD(T)={λ∈C:T-λI不是Drazin可逆算子}

令T的预解集和Weyl预解集分别为ρ(T)=Cσ(T)和ρw(T)=Cσw(T)。若E⊆C(复数集)，则isoE表示E中孤立点的全体且accE表示为E中聚点的全体。

2 主要定理

在给出本文的主要结果前，对一些记号和概念做出说明。

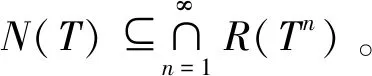
称算子T∈B(H)满足Weyl定理，若σ(T)σw(T)=π00(T)，其中π00(T)={λ∈isoσ(T):0

下面,我们利用新定义的谱集σ1(T)=accσw(T)研究算子T的Browder定理。

定理1令T∈B(H)，则下列叙述等价：

(i)T满足Browder定理；

(ii)σ(T)=σ1(T)∪σSF+(T)∪σk(T)；

(iii)σb(T)=σ1(T)∪σSF+(T) 。

(ii)⟹(i)要证T满足Browder定理，即证σw(T)=σb(T)。显然σw(T)⊆σb(T)，下证σb(T)⊆σw(T)。令λ0∉σw(T)，那么存在ε>0，当0<|λ-λ0|<ε时，T-λI为Weyl算子且λ∉σk(T)。因此λ0∉σ1(T)∪σSF+(T)∪σk(T)，从而λ∉σ(T)，即λ0∈isoσ(T)∪ρ(T)，于是由文献[7, 性质6.9]可知λ0∉σb(T)。因此σb(T)⊆σw(T)。

用同样的方法可以证明(i)与(iii)等价。

注解1(i) 在定理1中，当T满足Browder定理时，σ(T)分解的三块缺一不可并且σb(T)分解的两块也缺一不可。

例1令T∈B(l2)定义为：T(x1,x2,x3,…)=(0,x1,x2,x3,…)。

经计算可得T满足Browder定理,

σ(T)=σ1(T)=σb(T)={λ∈C:|λ|≤1}且σSF+(T)=σk(T)={λ∈C:|λ|=1}

显然,σ(T)≠σSF+(T)∪σk(T)且σb(T)≠σSF+(T)。

通过计算可得T满足Browder定理，

σ(T)=σb(T)=σSF+(T)={0}且σk(T)=∅=σ1(T)

显然，σ(T)≠σ1(T)∪σk(T)且σb(T)≠σ1(T)。

例3令T∈B(l2)定义为：T(x1,x2,x3,…)=(0,x2,x3,x4,…)。

经计算可得T满足Browder定理，另外σ(T)={0,1}，σ1(T)=∅，σSF+(T)={1}且σk(T)={0,1}。显然，σ(T)≠σ1(T)∪σSF+(T)。

(ii) 在定理1中，当σ(T)=σ1(T)∪σSF+(T)∪σk(T)或者σb(T)=σ1(T)∪σSF+(T)成立时，并不能推出T满足Weyl定理。

经计算可得σ(T)=σb(T)=σk(T)=σSF+(T)={0}且σ1(T)=∅。显然，σ(T)=σ1(T)∪σSF+(T)∪σk(T)且σb(T)=σ1(T)∪σSF+(T)。但T不满足Weyl定理。

下面，我们研究有界线性算子的Weyl定理。称T∈B(H)为isoloid算子，若λ0∈isoσ(T)时，有n(T-λ0I)>0。

定理2令T∈B(H)，则T为isoloid算子并且满足Weyl定理当且仅当

σb(T)=σ1(T)∪accisoσ(T)∪{λ∈C:n(T-λI)=∞}

证明必要性。设T为isoloid算子并且满足Weyl定理。显然

σ1(T)∪accisoσ(T)∪{λ∈C:n(T-λI)=∞}⊆σb(T)

另外，若λ0∉σ1(T)∪accisoσ(T)∪{λ∈C:n(T)=∞}，由于λ0∉σ1(T)可知λ0∈isoσw(T)∪ρw(T)，因此存在ε>0使得0<|λ-λ0|<ε时，有T-λI为Weyl算子。又因为T满足Weyl定理，故λ∈isoσ(T)∪ρ(T)。但由于λ0∉accisoσ(T)，从而可知λ0∈isoσ(T)∪ρ(T)并且n(T-λ0I)<∞。因为T为isoloid算子，因此λ0∈π00(T)∪ρ(T)，结合T满足Weyl定理可知λ0∉σb(T)。因此，σb(T)=σ1(T)∪accisoσ(T)∪{λ∈C:n(T-λI)=∞}。

利用与证明定理2同样的方法，我们可以得到：

T∈B(H)满足Weyl定理当且仅当

σb(T)=σ1(T)∪[accisoσ(T)∩σd(T)]∪{λ∈C:n(T-λI)=∞}

其中σd(T)={λ∈C:R(T-λI)不为闭集}。另外，通过定理2，很容易得到下面的结论。

推论1令T∈B(H)，则下列叙述等价：

(i)T满足Weyl定理；

(ii)σb(T)=σ1(T)∪accisoσ(T)∪σSF+(T)∪{λ∈C:n(T-λI)=0}∪{λ∈C:n(T-λI)=∞}；

(iii)σb(T)=σ1(T)∪[accisoσ(T)∩σd(T)]∪σSF+(T)∪{λ∈C:n(T-λI)=0}∪{λ∈C:n(T-λI)=∞}。

注解2(i) 在定理2中，若T为isoloid算子且满足Weyl定理，则σb(T)分解的三部分缺一不可。

①σ1(T)不可缺。

例5令T∈B(l2)定义为：T(x1,x2,x3,…)=(x2,x3,x4,…)。

通过计算可得σ(T)=σw(T)=σb(T)={λ∈C:|λ|≤1}，π00(T)=accisoσ(T)=∅且{λ∈C:n(T-λI)=∞}={λ∈C:|λ|=1}。显然，T有Weyl定理且为isoloid算子，但是

σb(T)≠accisoσ(T)∪{λ∈C:n(T-λI)=∞}

② accisoσ(T)不可缺。

显然，σ1(T)={λ∈C:n(T-λI)=∞}=∅且σb(T)=accisoσ(T)={0}。因此T为isoloid算子且满足Weyl定理，但是σb(T)≠σ1(T)∪{λ∈C:n(T-λI)=∞}。

③ {λ∈C:n(T-λI)=∞}不可缺。

经计算可得σ(T)=σw(T)=σb(T)={0}并且π00(T)=σ1(T)=accisoσ(T)=∅。因此T满足Weyl定理且T为isoloid算子但σb(T)≠σ1(T)∪accisoσ(T)。

(ii) 在定理2中，“T为isoloid算子”也不可缺。

由例2中的算子T可知T满足Weyl定理但不为isoloid算子。然而，

σb(T)≠σ1(T)∪accisoσ(T)∪{λ∈C:n(T-λI)=∞}

令π(T)={λ∈σ(T):T-λI为Drazin可逆算子}，由文献[8,定理10.2]可知π(T)⊆isoσ(T)。另外，若isoσ(T)⊆π(T)，那么称T为poloroid算子。因此，当T为poloroid算子时，有isoσ(T)=π(T)。下面，我们研究poloroid算子的Weyl定理。

当isoσ(T)=∅时，则T为isoloid算子且T为poloroid算子，此时σb(T)=σ(T)。于是有下列推论。

推论2令T∈B(H)，则isoσ(T)=∅且T满足Weyl定理当且仅当σ(T)=σ1(T)。

另外，当isoσ(T)为有限集时，有以下结论。

推论3令T∈B(H)，设isoσ(T)为有限集，则T为poloroid算子且满足Weyl定理当且仅当σ1(T)=σD(T)。

接下来，我们证明在一定条件下，若f(T)满足Weyl定理当且仅当σ1(·)满足谱映射定理。

推论4令T∈B(H)，设isoσ(T)=∅，且T满足Weyl定理，则对任意的f∈H(T)，f(T)满足Weyl定理当且仅当σ1(f(T))=f(σ1(T))。

证明若isoσ(T)=∅，则isoσ(f(T))=∅，此时由推论2知σ(f(T))=σ1(f(T))，故对任意f∈H(T)，f(T)满足Weyl定理当且仅当σ1(f(T))=σ(f(T))=f(σ(T))=f(σ1(T))。

另外，由Drazin谱映射定理[9]，同样可以得到下面的结论。

推论5令T∈B(H)，设isoσ(T)有限，则当T为poloroid算子且满足Weyl定理时，对任意f∈H(T)，f(T)为poloroid算子且满足Weyl定理当且仅当σ1(f(T))=f(σ1(T))。

事实上，关于σ1(·)的谱映射定理，我们有下面的结论。

定理4设T∈B(H)为isoloid算子且满足Weyl定理，则下列叙述等价：

(i) 对任意的f∈H(T)，f(T)满足Weyl定理；

(ii) 对任意的f∈H(T)，f(T)满足Browder定理；

(iii) 对任意的f∈H(T)，f(σ1(T))⊆σ1(f(T))；

(iv) 对任意的λ,μ∈Cσe(T), ind (T-λI)ind (T-μI)≥0。

证明(i)⟹(ii)显然。

(ii)⟹(iii)令μ0∈f(σ1(T))，且设λ0∈σ1(T)使得μ0=f(λ0)。若μ0∉σ1(f(T))，则存在δ>0使得0<|μ-μ0|<δ时，μ∈ρw(f(T))。设

f(λ)-μ=(λ-λ1)n1(λ-λ2)n2…(λ-λk)nkg(λ)

则由算子函数演算可得

f(T)-μI=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T)

其中g(T)为可逆算子。由于f(T)满足Weyl定理，故σw(f(T))=σb(f(T))，因此由Browder谱的谱映射定理有λi∉σw(T)(i=1,2,…,k)。对于λ0，存在ε>0使得0<|λ-λ0|<ε时有0<|f(λ)-f(λ0)|<δ。则f(λ)∈ρw(f(T))，因此λi∉σw(T)从而λ0∉σ1(T)，这与假设相矛盾。因此f(σ1(T))⊆σ1(f(T))。

(iii)⟹(iv)设存在λ0,μ0∈Cσe(T)使得ind (T-λ0I)=-m< 0

(iv)⟹(i)要证f(T)满足Weyl定理，即证σ(f(T))σw(f(T))=π00(f(T))。先证σ(f(T))σw(f(T))⊆π00(f(T))⟺σw(f(T))=σb(f(T))。显然σw(f(T))⊆σb(f(T))。另一方面，令μ0∈ρw(f(T))，设

f(T)-μ0I=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T)

显然λi∉σe(T)(i=1,2,…,k)。由条件(iv)可知λi∈ρw(T)。由于T满足Weyl定理，因此λi∉σb(T)，故μ0∉σb(f(T))。再证π00(f(T))⊆σ(f(T))σw(f(T))。令μ0∈π00(f(T))，即μ0∈isoσ(f(T))且0

f(T)-μ0I=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T)

不失一般性，假设λi∈isoσ(T)(i=1,2,…,k)。由于T为isoloid算子，因此对任意的λi，有λi∈π00(T)。再由T满足Weyl定理可知λi∉σw(T)，因此μ0∉σw(f(T))。综上可得f(T)满足Weyl定理。

最后，我们研究p-hyponormal算子和M-hyponormal算子的Weyl定理。 称T∈B(H)为p-hyponoromal算子，若(TT*)p≤(T*T)p；若存在正数M，使得对任意的x∈H，有M‖(T-λI)H‖≥‖(T-λI)*H‖，则称T为M-hyponormal算子。若T为p-hyponormal(或M-hyponormal)算子，那么T有以下性质：

(P1) 对任意的λ∈C，T-λI为p-hyponormal(或M-hyponormal)算子；

(P2)T为拟幂零算子,那么T为幂零算子；

(P3) 若E⊆H为T的不变子空间,那么T|E为p-hyponormal(或M-hyponormal)算子；

(P4)T有有限的升标。

定理5若T∈B(H)为p-hyponormal(或M-hyponormal)算子，则下列叙述成立：

(i)T为poloroid算子且满足Weyl定理；

(ii) 对任意的f∈H(T)，f(T)满足Weyl定理。

证明

(ii)设T为p-hyponormal(或M-hyponormal)算子。由(i)可知，当λ0∈isoσ(T)时，T-λ0I为Drazin可逆的， 此时n(T-λ0I)>0，因此T为 isoloid算子。 又因对任意的λ,μ∈Cσe(T)有T-λI与T-μI均有有限升标，故由文献[5,定理 3.4]可知 ind(T-λI)ind(T-μI)≥0。从而由定理4可得，对任意的f∈H(T)，f(T)满足Weyl定理。