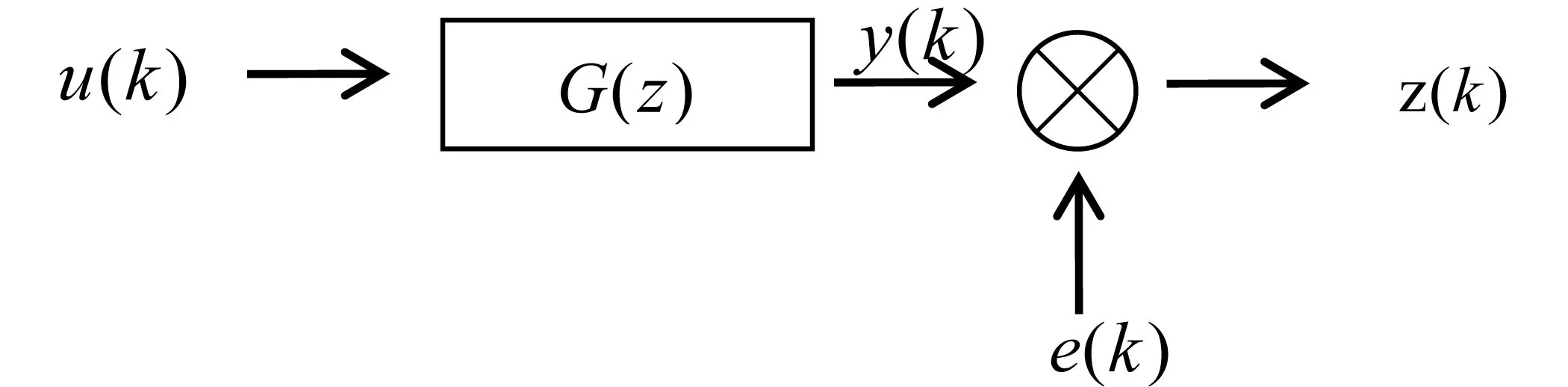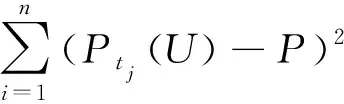最小二乘法及其应用
姜伟,付佳媛
(中国传媒大学 数据科学与智能媒体学院,北京 100024)
最小二乘法最早出现在勒让德发表的论著《计算彗星轨道的新方法》的附录中,在这本书中,勒让德利用最小二乘法使各方程的误差之间建立了一种平衡,从而防止了极端情况所施加的过多影响,并且有利于系统更加接近真实情况。然而,勒让德并没将最小二乘法在误差分析方面进行进一步的研究。而高斯则对此方法进行了更深一步的研究,他通过误差函数推出此方法并详尽地给出了其理论依据,并且将其应用于天体运动中。在1829年,高斯还提供了最小二乘法的优化强于其他方法的证明。随着最小二乘法的出现,它逐渐在统计学的回归分析及方差分析等上被广泛地应用,是一种非常重要的统计方法。如今,随着矩阵理论的深入研究及计算机技术的不断发展,最小二乘法应用于更多领域的数据优化处理中,如系统辨识、传感器、支持向量机等。
1 最小二乘法
最小二乘法是一种数值优化技术,通过使误差平方和最小化,从而得到最佳匹配函数。下面从微分、几何及概率论的三个角度来阐述最小二乘法的原理。
1.1 微分角度分析
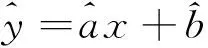
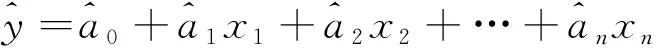
利用多元微分法,使s最小化,即s对各参数进行求偏导等于0,得
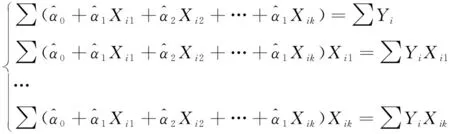
解这个线性方程组(此方程组也称正规方程组),可得k+1个参数的估计值αj(j=1,2,…,k)。当n=1时,则退化为一元线性回归。
1.2 几何角度分析
以求上述一元线性回归的参数为例,即求
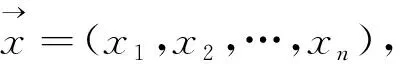
(1)
模的平方。那么,要使s最小化,即(1)向量的长度最短。为了更直观,下面以二维空间为例说明:
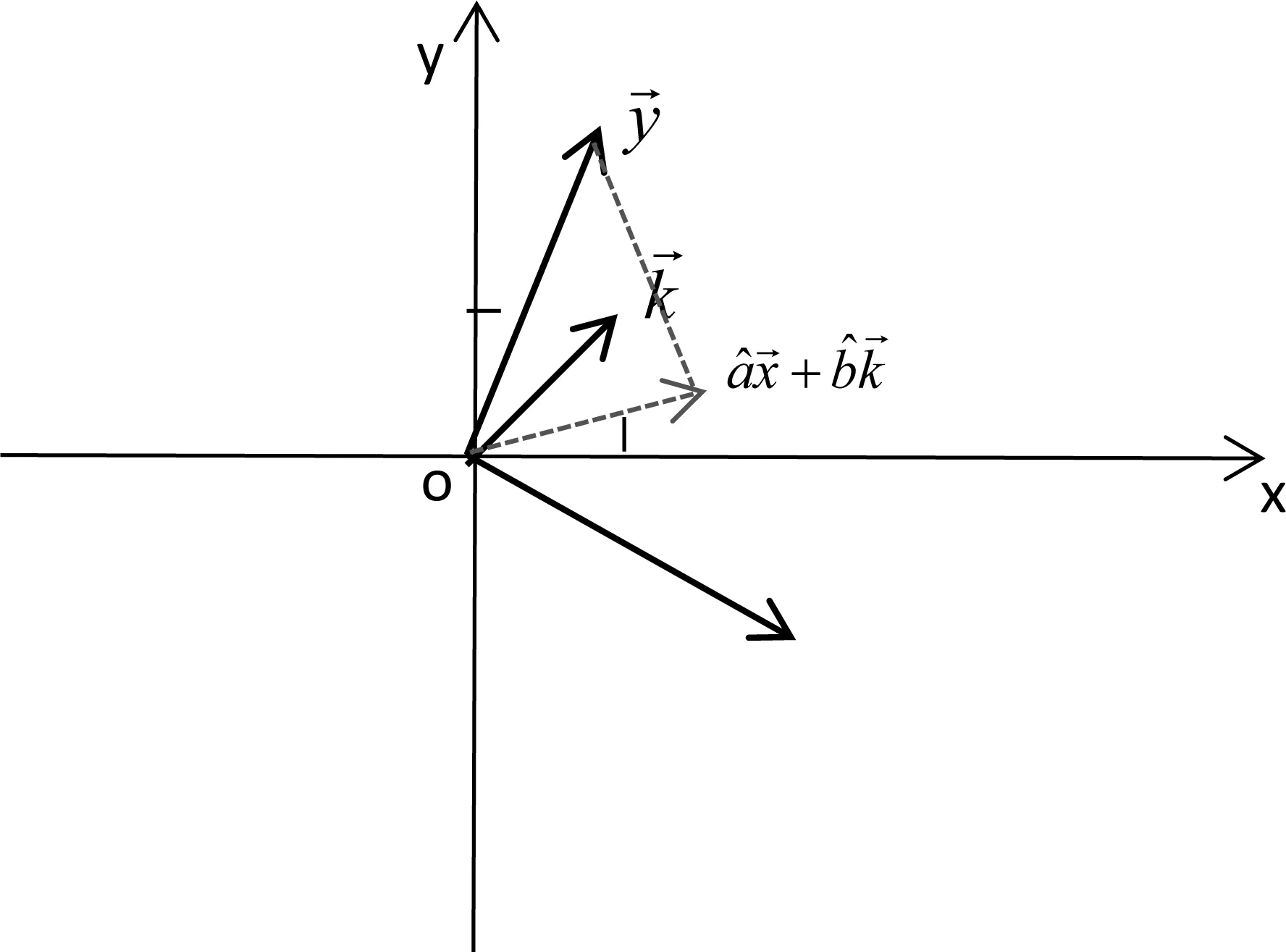
图1
1.3 从概率论角度分析
在n组相互独立的实验中,所得数据为{(xi,yi)|i=1,2,…,n} ,且数据点分布在直线y=ax+b附近。根据概率论知识,在干扰项服从零均值、同方差的正态分布假设下:
yi~N(axi+b,σ2)
那么,yi的概率密度函数为
由于yi是相互独立的,则y的联合密度函数为
在求参数估计值时,根据最大似然原理,使L最大,即使∑(yi-axi-b)2最小,则就转化为最小二乘法问题。也就是说,虽然两个方法出发原理不同,但在随机量满足正态分布时,可将最大似然法转化为最小二乘法。
2 最小二乘法的应用
2.1 最佳逼近解
设A∈Cm×n,b∈Cm,线性方程组为AX=b。当此线性方程组不相容时,希望求其近似解μ,使得对欧几里得范数‖•‖2,误差‖Aμ-b‖2达到最小。若∃μ∈Cn,使 ‖Aμ-b‖2≤‖AX-b‖2(∀X∈Cn),则称μ是方程组AX=b的一个最小二乘解。根据矩阵的Moore-Penrose广义逆的性质知,设A∈Cm×n,b∈Cm,A+是矩阵A的广义逆,X=A+b是AX=b的最佳的最小二乘解。
例 设一个质点运动的轨迹是椭圆,观测的点
(1,1) (0,2) (-1,1) (-1,-2)
在同一平面上,求拟合的最佳椭圆方程。
解 设椭圆方程α1x2+α2y2=1,将所观测到的代入得
可看出矩阵A满秩,则A+=(ATA)-1AT,可得
则可得最小二乘解
2.2 参数估计
参数估计,即根据已知模型的输入输出数据,对模型参数进行估计的过程。参数估计的方法有许多,最常用的方法可分为:矩法、最小二乘法、最大似然法。最小二乘法是以样本数据与估计值之差平方和最小来估计参数值的一类参数估计方法。
2.2.1 线性回归的参数估计
首先,介绍最小二乘法在一元线性回归中参数估计:
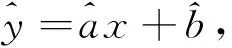
(2)
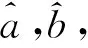
利用微分方法求解,s对求一阶偏导为0,即得到正规方程组
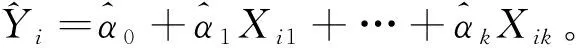
多元线性回归中的正规方程组的矩阵形式如下:
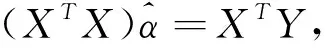
2.2.2 非线性回归的参数估计
在实际的生活问题中,由于研究问题中的变量之间常见的是非线性关系。在这些非线性关系中,有些非线性通过一定的方法可转化成线性,如指数型Y=abX可转化为对应的线性模型lnY=lna+Xlnb,然后根据最小二乘法原理进行回归分析。
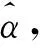
(3)
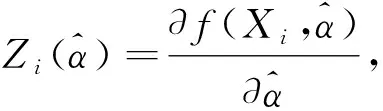
(4)
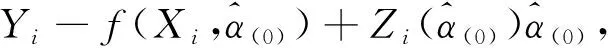
从最小二乘法用于非线性回归模型的过程,可以看出,最小二乘法还是对线性回归模型进行参数估计。
2.3 曲线拟合
曲线拟合,用连续曲线去拟合离散点的数据处理方法,即用近似函数逼近原函数。
其中h(x)=a1φ1(x)+a2φ2(x)+…+amφm(x) (m 在解决实际问题时,一般数据中不同点的所占的比重不同,因此考虑对εi加权重,即 使∑ωi[h(xi)-yi]2最小,利用微分法求解, 2.4.1 在系统辨识中的应用 系统辨识是现代控制理论的一个分支。随着控制理论应用日益广泛,控制过程复杂程度也在不断增大,并且其实际应用需要被控对象的数学模型。这些模型大多情况下是不知道的,或在正常运行下模型参数会发生变化。因此,在控制理论的应用中,首先需要建立被控对象的数学模型,系统辨识正是来解决此问题。 系统辨识是根据系统输入、输出时间函数,从一组给出的模型类中,确立一个能模仿被测系统真实行为的数学模型。经典的系统辨识的方法已经发展得较完善,如相关分析法、谱分析法、最小二乘法等,其中最小二乘法是最基础的、应用广泛的一种对于系统模型进行参数估计的方法,可以广泛地应用于动态、静态、线性、非线性系统。应用最小二乘法对系统模型参数进行辨识的方法有离线辨识和在线辨识。离线辨识是需要在得到模型的全部输入输出数据之后,用最小二乘法对其进行集中处理,从而可以得到系统模型的参数估计值。在线辨识是在系统运行中的一种递推辨识方法,由于占据计算机存储量小,从而得到广泛应用。 对于不同的系统进行辨识,它所对应的模型表达不同,以SISO系统为例, 其中u(k)、y(k)、z(k)分别为系统第k次输入值、输出真值、输出观测值,e(k)为不相关的白噪声且均值为0,G(z)为传递函数。输入输出关系为z(k)=u(k)G(z)+e(k),其中 将系统方程代入输入输出关系式,可得z(k)=φT(k)θ+e(k),其中θ为参数向量。对系统参数进行估计,利用最小二乘法,得 使J(θ)最小,即J对θ求偏导等于0,从而得最小二乘估计值θ=(φφT)-1φZ。 最小二乘法进行系统辨识也有一定的局限性,当系统噪声为有色噪声时,最小二乘估计值不是无偏一致的,因此会在最小二乘的基础上进行改进,从而会有广义最小二乘法、递推最小二乘法等进行系统辨识的参数估计。 2.4.2 在传感器上的应用 传感器是一种将感受到的信息按一定规律转化成便于处理和传输的信息的检测装置。根据感知功能不同,传感器可分为温度传感器、力传感器及光传感器等。由于感受器在输入到输出过程中会受到外界除所要接受信息以外信息的影响,从而对于结果的精确度会有一定的影响。因此,制作高精度的传感器,需要对其进行误差补偿。本文介绍利用最小二乘法对压阻式压力传感器进行温度误差补偿。 压阻式压力传感器是利用半导体的电阻率随应力变化的性质而制成的半导体器件。在被测压力作用时,电阻率发生变化,从而产生电压输出。在压力值不变的情况下,外界的一些其他因素会对输出的电压产生影响,其中由于半导体受温度较大,从而环境温度变化较大会使误差较大。因此,需要对传感器进行温度误差补偿。对于压阻式压力传感器的温度补偿,有硬件补偿和软件补偿,其中硬件补偿存在调试不变、精度不足等缺陷,而软件补偿会克服这些不足,因此会受到越来越多人的关注。软件补偿的方法有神经网络、插值法、最小二乘法等。 除以上应用外,它还会应用于其他许多领域,如高光谱图像数据处理、经济预测、农业实验分析等领域。不过,每一种方法都会有它的局限性存在,最小二乘法的局限性在于:对异常值很敏感;没有考虑自变量的误差;存在不可求解的情况等。因此,许多研究者会对最小二乘法进行进一步的改进,从而可以使它应用于更多领域,即会出现基于普通最小二乘法的广义最小二乘法、加权最小二乘法、两阶段最小二乘法等。在实际的应用中,还会结合实际情况与其他方法相结合进行应用。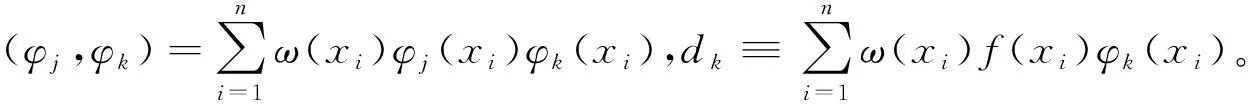
2.4 实际应用