基于非参数贝叶斯模型的列车卫星定位方法

刘 江 陈华展 蔡伯根 王 剑 刘靖远 陆德彪

(1.北京交通大学 电子信息工程学院,北京 100044;2.北京市轨道交通电磁兼容与卫星导航工程技术研究中心,北京 100044;3.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081)

列车测速定位始终是列车运行控制等领域研究与应用中关注的热点问题。随着列控系统的逐步发展,列车测速定位技术已逐步发展为车-地协同的运行模式,利用轨道电路、轨旁的应答器等实现列车占用检查及位置校正,车载设备采用轮轴速度传感器、多普勒雷达等传感器实时计算输出列车位置、速度等信息。目前欧洲下一代列控系统(NGTC)、美国主动列车控制系统(PTC)和日本先进列车管理和通信系统(ATACS)均已开始为适应未来智慧轨道交通发展而开展探索与布局,我国也已启动了下一代列控系统总体规划与关键技术研究,旨在以新的设计与应用框架对现有干线铁路、城市轨道交通采用的列控系统技术及装备进行协同,通过列控系统配置优化、性能提升、规范统一实现对未来市场及用户需求的有效适配。卫星定位因其实时、准确、全天候服务能力,已成为新型列控系统测速定位子系统的重要选择,对轨道电路、应答器等轨旁设备进行有效替代,深度提升测速定位的自主性、灵活性和成本效益。我国正在自主建设的北斗卫星导航系统BDS(BeiDou Navigation Satellite System)在航空、道路、水运等交通运输领域正在实施行业应用示范与推广,为将卫星定位技术引入下一代列控系统提供了重要契机。

引入多传感器信息融合技术[1],采用辅助定位传感器提供的冗余观测信息,如轮轴速度传感器[2]、惯性传感器[3]、多普勒雷达[4]、涡流传感器[5]等,对卫星定位的不利因素进行补偿,已被广泛纳入多种军事、民用领域的应用实施,为基于卫星导航系统构建列车安全定位体系提供了有益思路。通常利用状态估计技术进行融合解算,典型的如Kalman滤波器及其在非线性域的多种改进型算法,包括EKF、UKF、CKF 等[6-8]。然而上述算法均需在贝叶斯估计框架下基于先验分布的高斯假设得到递推形式。从贝叶斯方法的核心看,先验分布的选择是至关重要的决定因素,目前尚无统一的先验分布构造方法,单纯采用高斯分布作为假设并不能与随机、时变的现实情况有效匹配,从而使滤波器后验估计结果难以有效满足性能需求。基于非参数化蒙特卡洛(Monte Carlo)模拟思想形成的粒子滤波PF(Particle Filter),已成为一种重要的非线性递推贝叶斯估计方法[9],既可适用于非线性系统模型,又突破了高斯假设的限制,具有良好的适用性和可拓展性,但其也需面临观测噪声概率密度分布的不确定性问题。

非参数贝叶斯方法(Nonparametric Bayesian Method)逐渐受到研究人员广泛关注,是机器学习领域的一种数据分布拟合工具,随着数据变化,数据分布可以实现自适应的变化,实现模型参数学习和分类数目自动更新等任务[10]。其中,狄利克雷过程(Dirichlet Process)常作为先验分布应用于非参数贝叶斯模型,可以将一个复杂分布分解为多个分布分量,并确定各分布的权重,已在典型道路运行环境下的卫星定位观测误差建模等方向得到应用[11]。在此思路下,本文应用狄利克雷过程混合DPM(Dirichlet Process Mixture)模型对基于非线性滤波的列车定位计算进行改进,通过现场试验进行了验证,为有效适应列车定位过程特征及卫星定位观测环境提供了重要条件。

1 基于卫星导航系统的列车定位

因列车运行于确定的轨道空间,列车测速定位的主要目标在于实时确定列车沿轨道方向的走行距离及相应的纵向运行速度。为了引入卫星定位技术对列车运行位置进行估计,通常采用耦合结构将辅助定位传感器与来自导航卫星的观测信息进行联合,从而进行融合估计,在导航卫星信号受到遮挡、干扰等因素影响时确保定位解算的连续性和可用性。另一方面,借助轨道线路空间信息,通过地图匹配计算将包含观测、解算误差的坐标位置映射至一维轨道空间。在列车运行控制系统中,完整的基于卫星导航系统的列车定位子系统处理流程结构见图1。

图1 基于卫星导航系统的列车定位子系统流程结构

卫星定位解算通常采用观测伪距对未知坐标进行估计,通常用zk表示在k时刻由nk颗可视卫星获得的观测向量,即

式中:ρi为当前时刻第i颗卫星与车载卫星导航天线之间的伪距,i=1,2,…,nk,若考虑辅助定位传感器信息,可将其与位置、速度、方向相关的观测量列入zk使其进一步扩展。

在每个计算周期内根据所更新的观测向量zk,需要对未知的状态量sk实施状态估计

式中:待估状态量sk包含三维坐标(xk,yk,zk)以及时钟偏差量Δτk,通常采用最小二乘估计或Kalman滤波等递推估计逻辑获得估计解再利用其中所含位置分量)进行地图匹配与决策输出。

通常可认为伪距是卫星与接收天线间距离与加性误差分量的叠加,即

式中:ri为当前时刻第i颗卫星与接收天线间实际距离;c为光速分别为接收机以及第i颗卫星钟差;Ii、Tri分别为电离层、对流层信号传播误差;εi为伪距随机观测误差。

2 基于Dirichlet过程的非参数贝叶斯模型

Ferguson[12]于1973年首次提出了Dirichlet过程的定义:假设F0是测度空间Ω上的随机概率分布,参数α0是正实数,空间Ω上的概率分布F如果满足对测度空间任意一个有限划分B1,B2,…,Bm均有

则可以认为F服从基础分布为F0且Concentration参数为α0的Dirichlet分布,记作

式中:基础分布F0决定了模型中基本组成元素的分布,反之,若满足F～DP(α0,F0),则式(4)成立。

Dirichlet过程的灵活性在于它允许模型参数的实际先验分布F随机偏离基础测度F0,它是“关于分布的分布”。从Dirichlet过程中采样得到的分布是可数无限个离散概率,无法用有限数量的参数描述,因此,Dirichlet过程是典型的非参数模型[13],存在的3种典型构造方式,使其应用成为可能[14]。以中国餐馆过程(Chinese Restaurant Process)这一构造方式[15]为例,假设餐馆中有无数张桌子φ1,φ2,…每张桌子能够容纳无数个顾客,进入餐馆的每个顾客用标号θi表示,第1个顾客θ1进入餐馆选择一张桌子坐下,接下来顾客θ2进入餐馆后面临两个选择:与顾客θ1坐在一起,或选择另一张桌子坐下。随着顾客不断进入餐馆,顾客θn面临两种情况:选择有顾客就坐的桌子,即以正比于已经就坐于第j张桌子φj的顾客数mj的概率mj/(n-1+α0)就坐于桌子φj;或者以正比于α0的概率α0/(n-1+α0)选择一张尚无人就坐的新桌子,并使已被顾客占用的桌子总数N增加1,而φN～F0,θn=φN。构造原理见图2,其中,圆圈为餐桌,用φj表示,圆圈周围的矩形θn为就座顾客。

图2 Dirichlet过程的中国餐馆过程构造原理

将每张桌子看成一个群,选择该桌子坐下的顾客具有相同取值,令所有顾客表示为G1,…,Gn,将其中唯一的取值表示为G*1,…,G*m,具有该相同数值的顾客人数分别为g1,…,gm,则第Gn+1个顾客选择的预测分布为

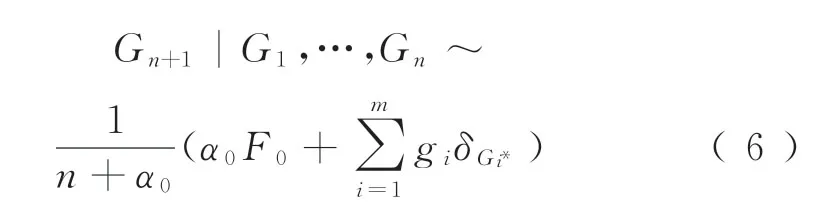
式中:δG*i为G*i点处的概率测度。由式(6)可以看出,gi越大则第Gn+1个顾客越有可能选择已选择过的桌子坐下,即越大的群越容易变得更大,这一状况也揭示了Dirichlet过程具有良好的聚类(Clustering)性质。为将具有一定相似性的不同组数据进行聚类,引入Dirichlet 过程混合模型DPM(Dirichlet Process Mixture),Dirichlet过程作为数据的先验分布存在,假设得到观测量zi,其分布服从

式中:C(θi)表示在给定参数θi时,观测量zi的分布。参数θi条件独立服从分布F,而观测变量zi条件独立服从分布C(θi)。当F服从Dirichlet过程分布时,该模型称为Dirichlet过程混合模型。

若观测集Z={z1,z2,…,zn}的数据独立,为得到每个观测的指示因子,即聚类βi,在利用Dirichlet过程作为先验分布的非参数贝叶斯模型中,利用Gibbs采样算法获得拟合密度函数特征。若Ω(t)用表示第t次循环采样时观测数据的分类结果,K(t)表示当前的聚类个数,基于(t-1)时的采样结果Ω(t-1)、K(t-1)、α(t-1),Gibbs采样算法主要通过3步完成:

Step1读入数据,并将n个观测数据进行随机排序,得到{τ(i)},i=1,2,…,n。

Step2令对于每一个数据i∈{τ(1),…,τ(n)},对每个数据的指示因子χi进行采样,并进行以下计算:

首先,基于现有的K个聚类,对每个聚类计算该观测数据的似然估计

然后,对χi依据以下分布进行采样

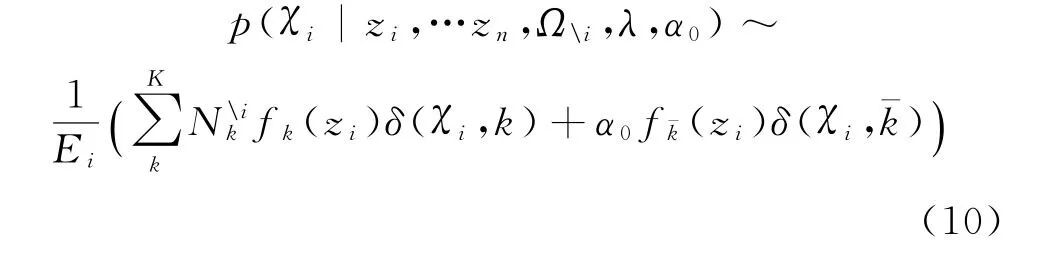
式中:分母Ei计算为

其中:为第k类内已有的数据量,若则将聚类的数量增加,即K=K+1。

Step3逐一检查各个类内的观测数据量,如果某一类的观测数据总数为0,则将该类删除,同时将聚类的数量减少,即K=K-1。

通常选择θi～F0和zi～C(θi)为共轭分布,使采样过程的计算简单可行。

3 基于非参数贝叶斯模型的定位估计方法

列车运行过程中在k时刻接收到nk颗卫星伪距观测信息,可将每颗卫星的伪距作为该时刻一个传感器的观测量参与基于DPM模型计算。考虑式(3)所述伪距观测模型,卫星钟差、大气传播误差(对流层、电离层误差)可通过接收机建模处理,则观测模型可进一步简化为

式中:bi、分别为观测误差的未知误差分量、白噪声分量。

可将εi特性分别描述为:

(1)常规模式:卫星定位观测质量未受到空间地形以及随机干扰因素影响,未知误差分量等于或近似为0,即满足bi=0,伪距误差εi与同分布,服从零均值且方差为确定水平的正态分布εi～N(0,σ2)。

(2)退化模式:观测量存在概率密度分布未知的误差,bi因环境或干扰因素的不利影响无法忽略,即bi≠0,则其与叠加后的分布特性依然难以获知,引入DPM模型的目的即在于如何对其进行有效描述并将结果引入定位解算过程。

根据上述思路,在存在未知误差分布特性的条件下,对列车卫星定位解算过程建立状态空间模型为

式中:xk为待估状态向量,其元素为三维列车位置与速度分量;f(*)、h(*)分别为系统状态转移过程及量测过程的非线性函数;uk、εk分别为系统噪声向量和量测噪声向量,这里假定系统噪声服从已知的固定分布,而重点关注不定的量测噪声分布Q。

基于贝叶斯估计思想,假定先验概率密度已知,对于未知的状态参数可以使用初始分布Markov过程p(x0)、状态转移概率p(xk|xk-1)(见式(13))以及条件概率p(zk|xk)建立如下模型。

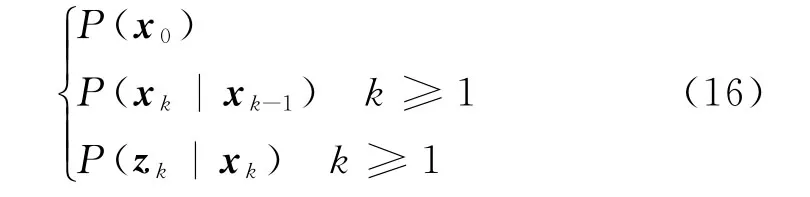
根据上述模型,贝叶斯估计的主要目标在于利用所获得的量测集z1:k={z1,z2,…,zk}对后验概率密度p(x0:k|z1:k)及其边界分布p(xk|z1:k)进行求解。若假设未知的分布Θ的形式已知,但其参数向量θ无法准确获知,从θ服从的先验密度p(θ)以及分布Θ的一个k个独立样本集{ε1,ε2,…,εk}出发,若能解决后验密度p(θ|ε1:k)估计问题,则求得滤波估计解p(xk|z1:k)将成为可能。然而,量测噪声序列ε1:k无法直接在传感器观测过程中获得,为了有效求解后验密度p(θ|ε1:k)并用于状态估计,引入DPM模型并利用Gibbs采样获得拟合密度函数的特征。

考虑卫星导航伪距观测误差的非平稳性,其短期观测误差可通过一个高斯分布近似,但其均值、方差参数具有时变性,难以用一组确定参数准确描述。为此引入DPM模型产生一个无限高斯混合,其均值、方差等参数用θ=(μ,V)描述,则后验密度p(θ|ε1:k)求解的关键环节即为如何确定实际高斯混合的个数及其相应参数。根据式(15)所述分布特性,定义量测误差的概率密度函数为Θ,则其无参数模型估计为

式中:f(ε|θ)为混合概率密度函数;F为混合的分布,基于所采用的DPM模型,其服从Dirichlet过程先验的随机概率测度F～DP(α,F0),在此条件下,DPM模型为

其中,先验概率θj～F(θj)与似然度εj～f(εj|θj)可将其转化为基本贝叶斯模型形式。

依据上述模型,其实现过程主要集中于精度参数α以及基础分布F0的选择上。首先,假定分布参数值θj=(μj,Vj)集中于有限数量的参数聚类上,设该数量为χ个,为了对精度参数α进行采样,需确定χ的先验分布以明确聚类混合中正态分量的数量。文献[16]给出了一种基于Gamma分布的采样方案:假定α服从Gamma分布α～Γ(a,b),其中a、b分别为形状参数和尺度参数,则p(χ|α,k)可由两个Gamma后验分布集成表达,再通过对χ与α的采样结果计算更新α值,基于Dirichlet过程采样得到其期望为

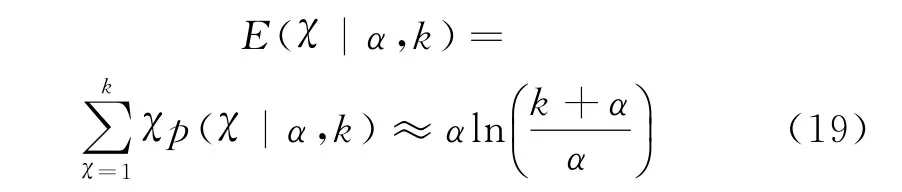
利用上述方式可确定聚类中正态分量的数量,并确保其随着观测数量的增加呈近似对数增长趋势。

其次,取F0为由未知均值μ、方差V决定的正态分布,为了确定分布参数值,这里根据前述卫星伪距观测模型的常规模式、退化模式的划分,利用伪距预测误差将当前观测质量的类型与分布参数F0的确定关联起来。在每个周期计算状态预测量|k-1,提取三维位置分量计算每颗卫星伪距残差rk,i为

在每个周期将每个可观测卫星的伪距残差rk,i加入Dirichlet过程混合模型,经过Gibbs采样聚类,得到伪距误差密度函数的特定描述。基于上述思想对运用DPM模型用于列车定位解算的过程进行总结:在获得若干卫星观测信息时,将所有伪距观测量抽象为一个伪距观测误差的概率密度描述,将伪距预测残差引入DPM模型得到有限个高斯分布混合的参数及相应的权重系数,分别在这些参数分布条件下进行状态滤波估计,对各估计结果进行加权合成,得到最终状态估计结果。本文提出的基于非参数贝叶斯模型的定位估计流程主要分为以下5个阶段:

Step1初始化 确定滤波器初值,包括、P0以及滤波估计参数,如Qk值及Hk结构等。

Step2时间更新

(1)利用系统状态空间模型计算待估状态向量的一步时间预测|k-1,即

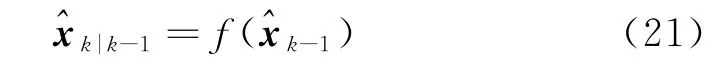
(2)基于预测结果|k-1及更新观测集中经过校正的伪距{ρk,i}计算残差rk,见式(20)。

Step3高斯混合更新

(1)为Dirichlet过程混合模型加入伪距残差,可表达为AddRes(DPM,rk)。

(2)Gibbs采样与聚类,获得有限个高斯分布混合,其数量为lk,相应的分布参数为

Step4量测更新(非线性估计,以EKF 估计为例)

(1)对应每个高斯分布混合,更新其一步预测方差矩阵为

式中:Φk|k-1为非线性系统状态转移函数f(*)的线性化近似所得状态转移矩阵,在EKF估计框架下同样适用于式(21)所示一步预测计算。

(2)计算Kalman滤波增益矩阵为

式中:Hk为非线性量测函数h(*)的线性化近似所得量测矩阵是跟随分布参数更新的量测方差矩阵,是对角线元素为高斯方差的(nk×nk)维对角阵

(3)计算每个并行滤波器的状态估计解为

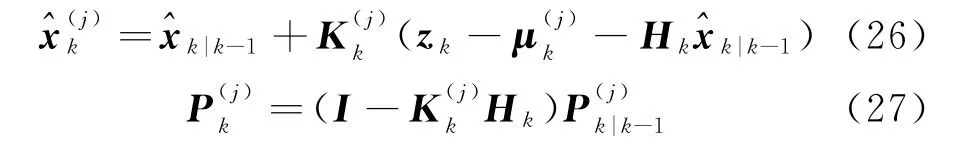
Step5加权输出

基于权重系数对各滤波器所得估计解进行加权联合,得到最终状态估计解及其方差为

基于上述5个阶段的计算流程,在每个估计周期内采用nk颗可视卫星的伪距原始观测,结合系统状态预测量更新伪距残差,基于DPM模型驱动高斯分布混合的更新,用于若干个分布对应的子滤波估计过程分别进行量测更新计算,最终通过加权获得联合状态估计结果,送至列车位置信息转换接口更新位置报告。

4 方法验证与分析

分别采用仿真数据和实测数据对本文所提出的定位估计方法进行验证分析。首先,为了使用明确的参考真值对引入DPM的作用进行评估,以2016年在青藏铁路现场实验中获得的高精度卫星定位数据作为数据源创建仿真场景及数据。原始轨迹数据采集中,利用Star Fire星站差分技术实现星基差分定位,数据采集接收机全程工作在差分定位模式,平均海拔4 621.21 m,可见卫星数、水平精度因子HDOP分别稳定在8颗、1.2,沿线无明显卫星信号遮挡。原始列车运行轨迹区段见图3。

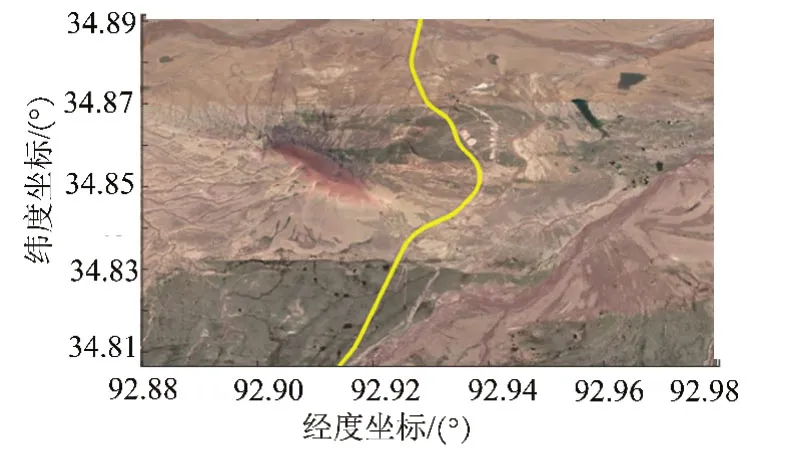
图3 原始列车运行轨迹示意

在轨迹回放过程中,为了对所提出的定位估计方法性能进行验证,设计了两种仿真场景用于对比:

(1)仿真场景1:直接采用原始回放信号,比较评估接收机的输出与采用本文方法的解算结果。

(2)仿真场景2:在原始轨迹回放过程中,在第120、180 s分别对两颗可观卫星增加最大强度为30、20 m的伪距偏移,利用模拟器自带模型改变伪距观测量的误差特性,在评估接收机中接入模拟卫星信号,比较其输出与采用本文方法的解算结果。

仿真场景1条件下,评估接收机解算结果与基于DPM的估计结果的东、北向误差和水平位置误差比较结果见图4。为了对误差对比情况进行量化分析,定位误差的均值、方差及最大值的统计结果见表1。

从上述结果可以看出,在仿真场景1给定的常规观测条件下,两种解算方式所得误差水平相当,DPM估计误差均值在东、北向表现各异,相较于评估接收机解算增大了92.54%、降低了10.95%,标准差分别降低了70.28%、11.67%;在水平估计误差方面,基于DPM的估计误差均值、标准差相对于接收机解算结果略有增高,分别增大了4.25%、19.12%。

图4 仿真场景1东向和北向位置误差、水平位置误差比较

表1 仿真场景1位置估计误差统计结果 m

仿真场景2两种方案估计结果的东向、北向误差见图5(a)、5(b),水平位置误差见图5(c)。由于两种方案所得误差值数量等级有较大差异,为显示误差时变细节,图5中的纵坐标按照不同值域尺度进行复用。

仿真场景2定位误差均值、方差及最大值的统计结果见表2。由表2可以看出,伪距偏移的注入对评估接收机的直接解算过程产生了明显影响,与未注入偏移时相比发生了明显退化,东向误差表现更为显著。与评估接收机解算结果相比,基于DPM的东向、北向误差均值分别降低了90.25%、48.05%,标准差降低了98.47%、89.03%;在水平误差方面,基于DPM的估计误差均值、标准差降低了87.06%、97.24%。虽然与仿真场景1相比,基于DPM的估计误差量级有所增大,但在同等条件下与评估接收机解算相比,其精度水平更为稳定,对所注入的伪距偏差具有较低敏感性。

图5 仿真场景2东向和北向位置误差、水平位置误差比较

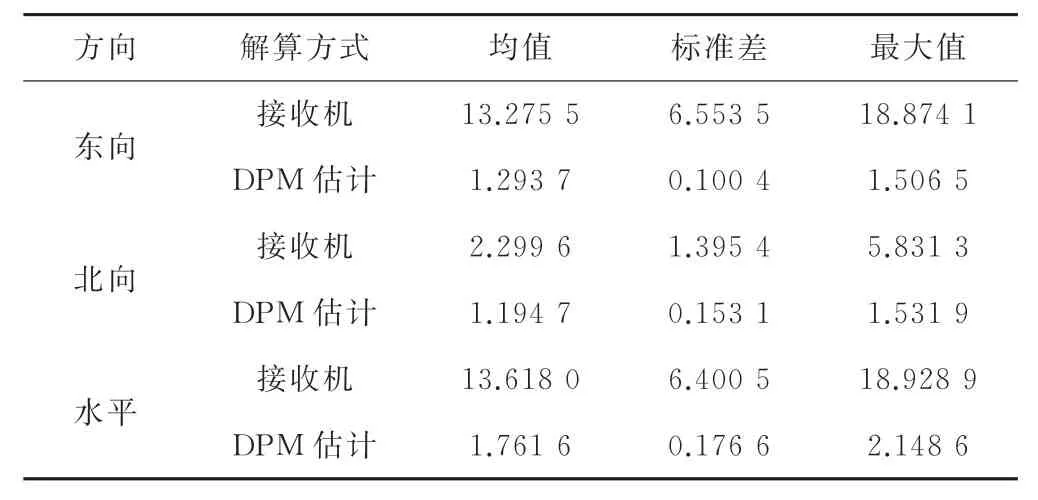
表2 仿真场景2位置估计误差统计结果 m

为进一步检验实际性能,采用2015年11月在青藏线“纳赤台—小南川”实测数据用于性能分析,实验列车运行轨迹见图6,检测车内部的实验设备安装情况见图7,实验区段内可见卫星数与水平精度因子HDOP值的时变情况见图8。

图6 现场实验列车运行轨迹示意

在现场实验中,采用自制实验系统搭载接收机接收、处理卫星信号进行定位解算,为了评估定位性能,采用两套高精度参考系统作为评估基准:

(1)参考系统1 Navcom 2050型接收机,工作于星基差分定位模式。

图7 检测车内实验系统及定位参考系统

图8 现场实验中观测卫星数及精度因子时间分布

(2)参考系统2 Nov Atel SPAN-FSAS系统,由ProPak6型卫星定位接收机与iMAR FSAS光纤陀螺构成高精度组合系统。

实验系统采用常规单点定位解算模式,在运行环境发生变化,尤其是铁路沿线地形环境对卫星信号形成遮挡、反射等情况下,定位性能将受到显著影响。两组典型系统的运行轨迹见图9。一个典型的列车定位性能劣化场景见见图9(a),实验系统定位结果存在明显偏差,正常水平场景见图9(b)。

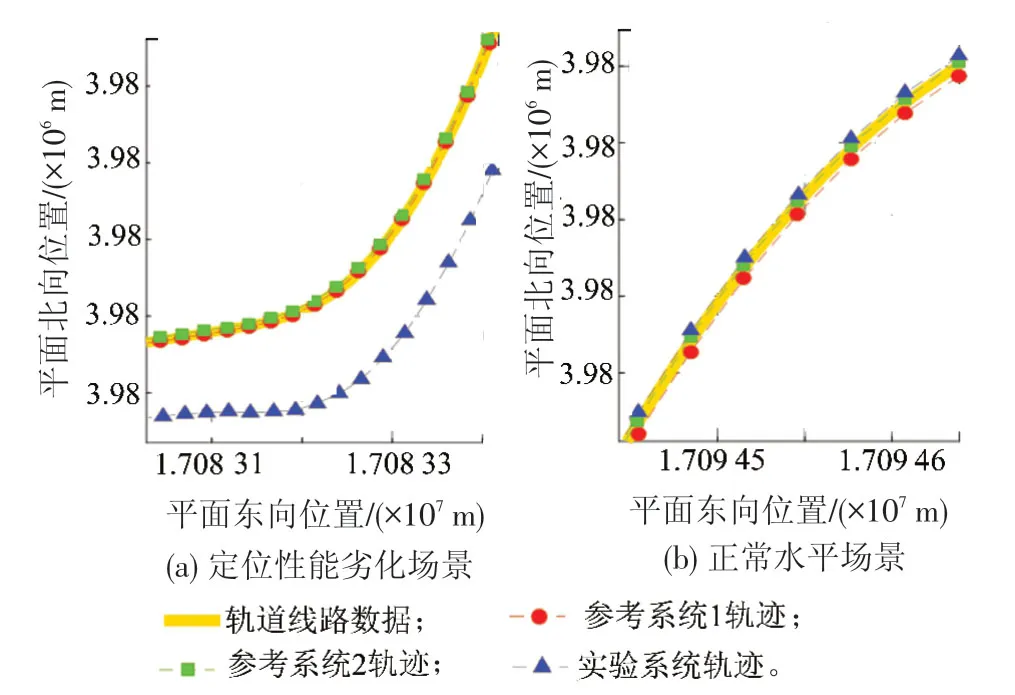
图9 实验系统与参考系统的运行轨迹(局部视图)

采用基于DPM模型的估计方法进行运算,与实验系统进行比较,以两种参考系统为基准的东、北向误差对比结果见图10、图11。由于两类北向误差量级相差较大,为突出细节,实验系统北向位置误差全局视图见图12。自460 s开始出现的北向精度劣化对应了图9左图所示轨迹区段。

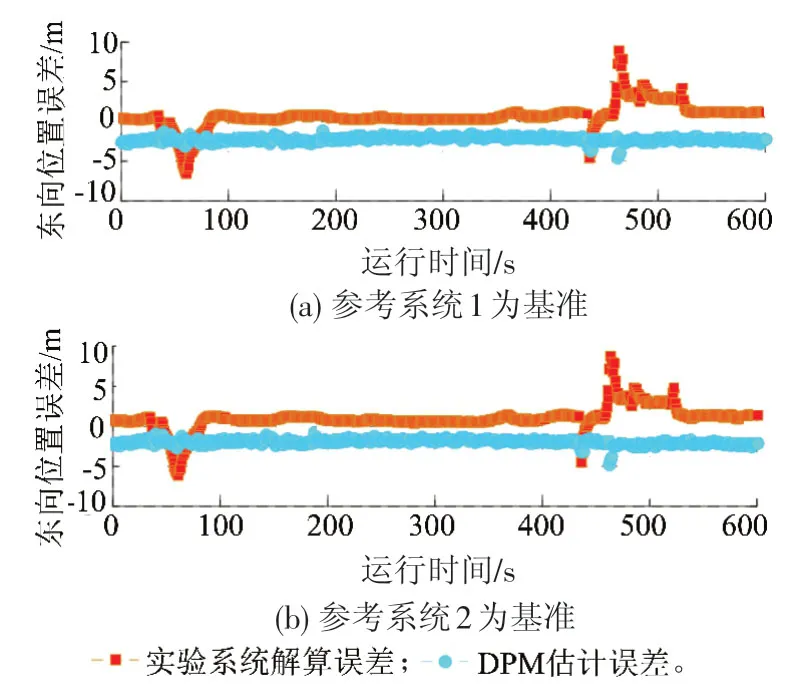
图10 现场实验东向位置误差比较

图11 现场实验北向位置误差比较

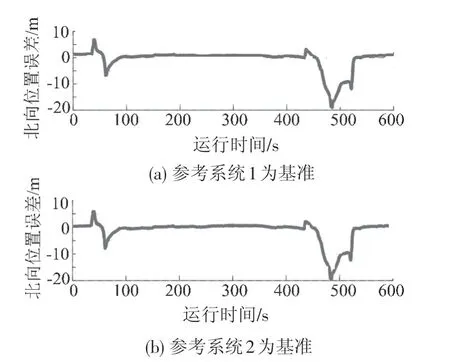
图12 实验系统北向位置误差全局视图

现场实验条件下的水平位置误差见图13,类似地,实验系统水平位置误差的全局视图见图14。由图13可见,实验系统在大部分情况下的定位误差处于正常水平,但自39、460 s开始出现两段明显波动,其发生过程可直接由图8所示观测卫星数与水平精度因子的变化情况进行反映。对东、北向及水平误差进行量化分析,采用两套参考系统所得位置误差的统计结果见表3、表4。

图13 现场实验水平位置误差比较

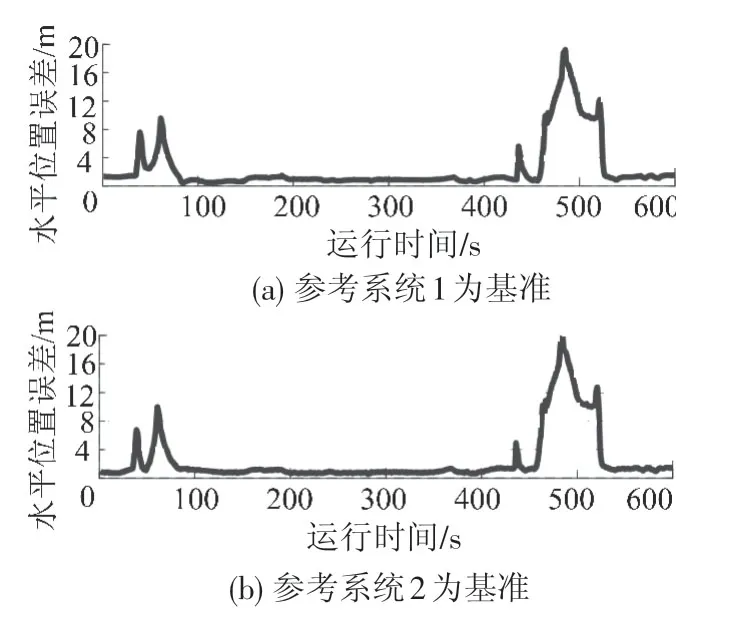
图14 实验系统水平位置误差全局视图

表3 现场实验位置估计误差统计结果(参考系统1)m

表4 现场实验位置估计误差统计结果(参考系统2)m

可以看出,以两套参考系统为基准所得结果的趋势一致,采用基于DPM的估计的东向误差均值相对实验系统有所增大,北向误差均值有所降低,而其标准差始终保持在较低水平。从水平误差来看,基于两套参考系统的DPM 估计误差分别降低了3.59%、16.68%,标准差降低了89.65%、87.11%,误差峰值分别降低了69.75%、67.81%。总体来看,采用基于DPM的估计与实验系统相比,对定位性能的改善主要体现在卫星信号观测条件变化情况下的精度水平维持和总体精度水平的稳定性两个方面。DPM 这一非参数贝叶斯模型使定位性能有效适应运行观测条件,特别是在卫星观测特性异变但尚不足以被常规故障检测逻辑进行识别、隔离的情况下,其特点更具实用效益,符合列车控制系统的特定需求。

地图匹配是实际列车控制应用中确定一维位置描述的必要环节,匹配残差提供了另一种对位置解算性能的评估途径,匹配残差比较结果见图15,地图匹配计算前后的局部轨迹结果见图16。

图15 现场实验轨道地图匹配残差比较

图16 定位轨迹比较与地图投影结果(局部视图)

基于两类定位解算方式所得匹配残差的统计结果见表5。

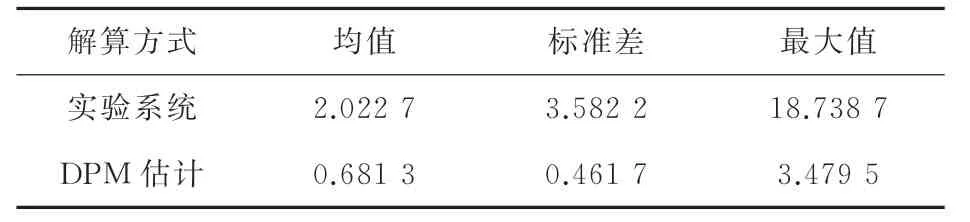
表5 轨道横向地图投影残差统计结果 m

基于DPM的估计所得匹配残差均值相较于实验系统降低了66.32%,标准差降低了87.11%,残差峰值降低了81.43%。轨道电子地图提供的评估参照,进一步反映了基于DPM的定位估计方法的优势,与前述参考系统得到的评估结果一致,为其与卫星定位自主完好性监测、故障检测隔离等计算决策逻辑集成并构建列车安全定位系统方案提供了良好基础。

5 结束语

基于卫星导航系统实现列车测速定位在列车控制系统等应用中具有显著优势,如何解决卫星观测误差特性的不确定性与定位解算中采用确定分布假设条件之间的失配问题,是决定列车卫星定位性能的关键因素。本文针对此问题,运用基于Dirichlet过程混合的非参数贝叶斯模型,构造了基于DPM的多滤波器加权联合估计方法,打破了单一的观测特性假设带来的制约。基于实测数据及专用设备进行的仿真计算与采用现场数据及高精度参考系统进行的实际验证,分别验证了本文所述方法在卫星观测特性存在异变条件下具备的不敏感性和适应性,相对于对比系统的定位解算能够获得更加稳定的精度水平,在基于卫星导航的列车控制等未来应用方向上具有显著的实用潜力。

论文所述方法并不完全适用于所有类型的列车运行环境和卫星观测条件,对于一些极端条件与故障失效状态,需进一步与其它防护隔离逻辑联合实现有效应对。为此,后续工作中将进一步研究所述退化模式的精细建模与相应的DPM 动态更新方法,结合现场实验探索滤波器系数的在途调整策略。此外,与融合估计之外的其它处理逻辑集成,构建安全定位系统,实施定位安全评估与现场测试,将是后续工作逐步向实用层次推进的重要方向。