一种基于策略梯度强化学习的列车智能控制方法
张 淼 张 琦 刘文韬 周博渊
(1.中国铁道科学研究院集团有限公司 研究生部,北京 100081;
2.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081;3.国家铁路智能运输系统工程技术研究中心,北京 100081;4.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
尽管城市轨道交通被称为“绿色交通”方式,具有快速、便捷、运量大等特点,但大规模及高密度的运营使得城轨系统的能耗急剧增长。其中取决于列车站间控制策略的牵引能耗约占系统总能耗的50%。因此为减小系统能耗、削减运营成本,列车节能运行成为近年来的研究热点。
为减小列车的牵引能耗,国内外诸多学者对列车控制策略的优化方法进行了大量研究。其中庞德里亚金极大值原理在早期的研究中得到了广泛应用。Asnis等[1]分析了列车最优控制问题,得到了最优速度曲线的必要条件。徐凯等[2]针对城轨列车控制系统运行模式曲线的设计需求,在满足安全、精确停车及各种约束条件下,以运行时间和能耗为目标,建立列车运行的多目标优化模型,并将粒子群优化PSO算法与布谷鸟搜索CS相结合,即多种群分层PSO-CS联合优化算法。Albrecht等[3]考虑了信号显示对列车运行的安全约束,利用经典的有约束优化方法,研究了在非水平轨道上同向而行的两列车在满足运行时分条件下的列车节能驾驶问题,得到了最小化总牵引能耗的必要条件,证明了每列车的最佳驾驶策略由每个区段上的最佳驾驶速度唯一确定。考虑到变化的坡度和限速条件,Khmelnitsky[4]利用极大值原理分析了最优解的解析性质,并提出了一个数值算法求解列车节能速度曲线。Liu等[5]应用极大值原理来求解节能驾驶策略,并给出最优工况序列和切换点的解析解。除此之外,Albrecht等[6-7]研究了列车在陡坡线路条件下运行的节能驾驶策略,得到了最佳切换点的必要条件,并通过扰动分析证明了最佳切换点的唯一性。Ke等[8]利用“最大-最小”蚁群算法求解了地铁列车在区间的节能运行速度曲线,并有效提高了算法的计算效率。Su等[9-10]构建了牵引效率可变条件下的城轨列车节能控制优化模型,并提出了一种基于能量分配的数值算法求解列车节能驾驶策略。
另外,还有许多学者利用智能控制方法研究了列车运行优化控制问题。Cheng等[11]以安全、准点、节能和舒适度为优化目标,设计了包括专家系统和在线优化算法在内的高速列车智能驾驶方法(iDMS)。在不利用精确的列车模型和离线目标速度曲线的情况下,Yin等[12-14]基于专家知识,分别利用梯度下降法、强化学习和数据挖掘方法,提出了列车智能驾驶算法。另外,Zhang等[15]将数据挖掘算法与专家知识结合构建了3个数据驱动的列车运行模型(DTO),并通过一个启发式的列车停车算法改进这些模型,从而保证停车精度。为了估计城轨列车的停车误差,Chen等[16]引入软计算方法构建了新的列车模型,并通过调整模型的参数有效地减少停车误差。为解决列车自动停车控制问题,Chen等[17]利用强化学习方法,基于应答器提供的精确位置数据提出了一种在线学习控制策略。针对重载列车在长大下坡区段运行情景,Huang等[18]利用神经网络设计的列车驾驶曲线生成方法,得到列车在循环制动时的减压量,从而有效保障列车的运行安全。Wang等[19]提出了一种基于迭代学习控制的算法,该算法通过充分利用历史运行数据中的可用信息来调整列车当前的驾驶策略。李诚等[20]提出一种基于粒子群算法的列车节能控制算法。
在实际中,列车牵引能耗取决于车载列车自动驾驶系统ATO中采用的控制策略。传统ATO系统的控制方法包含两层,其中上层为规划层,旨在根据给定的站间运行时间设计一条目标速度曲线;下层则负责控制跟踪该目标速度曲线。这种控制方式可以精确跟踪目标速度,保证列车在站间的准点运行,但也会使得列车频繁切换控制工况,导致乘客舒适度下降和运行能耗的增加。
现有ATO系统通过结合优秀司机的驾驶经验来调整下层的控制方法,在目标速度vtarget附近进行牵引-惰行控制模拟司机的驾驶操纵过程。该控制方法可描述为“减a减b”策略,即当速度值达到目标速度减a时,列车采用惰行工况减速运行;当速度值降至目标速度减b时,列车切换为牵引工况加速运行,见图1。这种控制方式能增大列车的惰行距离,从而减少列车牵引能耗,能够有效减少工况切换次数,提高乘客舒适度。然而其站间运行时间可能会和列车时刻表中的计划运行时间有一定偏差。特别是异常条件下,系统参数呈现出非线性和时变的特性,使得这种基于确定模型的控制策略将不再适用。
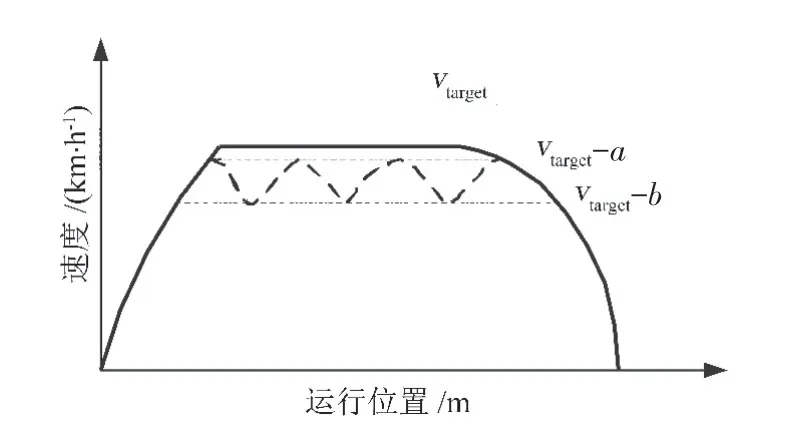
图1 现有ATO系统的控制原理
综上所述,当前列车控制问题的挑战之一是如何得到一种灵活的控制策略,既能提高列车的准时性和节能性,还可以处理参数的不确定性。基于强化学习的智能控制是当前人工智能领域的重要发展方向,由于其不需要精确的模型信息,使之成为解决列车最优控制问题的有效方法之一[21]。因此,在现有的ATO控制原理和优秀司机的驾驶经验的基础上,本文提出了一种基于策略强化学习的列车智能控制算法,该算法在减少列车能耗的同时,可保证良好的准时性和乘客舒适度。相较于现有控制算法,本文提出的智能控制算法特点是:
(1)不依赖具体的列车动态模型,控制过程不需要参考速度曲线,可以利用历史运行数据来训练得到一个性能良好的控制器,使其适应系统参数的非线性和时变性。
(2)可以利用智能控制器生成的列车运行数据进行再训练,不断优化自身性能,从而实现控制器的自学习过程。
1 问题描述
城市轨道交通线路的站间距短,且列车的牵引和制动性能良好。一般城轨列车的站间控制过程分为出站启动、站间速度保持和进站停车3个阶段。在启动阶段,列车获得在短时间内达到高速的牵引力,增加城轨系统的平均运行速度;在速度保持阶段,列车利用牵引-惰行来保持速度;在停车过程中,列车减速并在站台上精确停车。对于城轨交通系统列车的运行安全由列车自动防护系统ATP 防护。ATO系统旨在提高城市轨道交通系统的效率。考虑到ATO系统的控制策略,城市轨道交通的运行效率侧重于提高运行准时性、节能性和乘客舒适度。这3个性能指标的定义分别为:
(1)准时性是城轨系统运营的一个重要指标。尤其是在高峰时段,相邻两列车的追踪间隔短且行驶路径有限。某列车发生的小延误很容易传播到其他多列车,甚至影响整个系统。此外大的延误可能影响乘客对其他线路或其他运输方式的换乘效率。列车的准时性可用列车计划运行时间T和实际运行时间T′的时间误差et来衡量

(2)舒适度 ATO系统决定了列车的控制策略。在惯性的作用下,车内乘客随着车辆移动。在本研究中,用加速度和其变化率来量化车体运动对乘客舒适度的影响。在城轨系统中,基础设施较为简单且站间距短,因此本文不考虑曲线舒适度和连续的乘客舒适度,只考虑离散的乘客舒适度PDE,具体的评价方法将在2.1节中给出。
(3)节能性 随着能源价格上涨和人们对环境问题的关注,列车运行中的能效显得日益重要,这也是研发所提出的智能控制算法的主要考虑因素。列车在站间运行的牵引能耗[22]表示为

式中:F为列车牵引力;S为站间距离;v为列车速度;x为列车位置。
2 求解方法
2.1 专家系统
专家系统包括从文献、司机经验和运行数据中总结出来的节能控制工况,以及为满足乘客舒适度而构建的列车控制规则。
考虑城轨列车的牵引效率,文献[8]证明了列车的节能运行工况由最大牵引、惰行和最大制动构成,并对这种节能运行工况的描述为:
(1)最大牵引和最大制动 列车加速或制动的速度越慢,站间运行所需的时间就越长。为了以较低的加速度或制动速率获得相同的运行时间,列车应该加速到更高的速度,而这将会消耗更多的能量。因此在启动加速和制动停车阶段,分别采用最大牵引和最大制动工况是最节能的控制方式。
(2)惰行 在不施加牵引力和制动力的惰行阶段,列车依靠惯性向前运行且不消耗能量。因此,列车惰行越早,能耗越低。
具体操作时列车在启动出站阶段应施加最大牵引,加速至较高的速度;在途中运行时,列车采用最大牵引和惰行工况来节省能量,且为了满足运行时分的要求,需在加速和惰行工况之间进行切换,在进站阶段,列车采用最大制动停车。
(3)舒适度 基于文献[23],本文将乘客舒适度简化定义为与三维加速度相关的PDE。对于城轨系统,横向和垂向加速度主要由基础设施和车辆决定,纵向加速度则与ATO控制策略密切相关。通过分析列车启动过程的运行数据可知,实际运营中的列车加速度符合乘客舒适度标准中的约束。因此启动过程的控制策略可以直接用作专家系统的一部分。
综上所述,构建了保障乘客舒适度的专家系统,利用该专家系统能产生列车启动过程的控制策略和途中运行的“牵引-惰行”切换策略。用于列车控制的专家系统推理机制为:
①如果vt=0且F>0,则启动阶段的控制序列为F1。
②如果vt=vtarget-b且Ft+1>0,则惰行转牵引的控制序列为F2。
③如果vt>0且x>xb,xb为停车位置,则制动阶段的控制序列为B1,直到减速至0。
④如果vt=vtarget-a,则牵引转惰行的控制序列为F3。
在专家系统中,所有控制序列均满足舒适度的约束,并集成了特殊区段和场景下的节能驾驶经验,即

2.2 基于策略的强化学习方法
本文提出的基于策略的强化学习算法PBRL(Policy-Based Reinforcement Learning),确定在每1个小区间内的最佳的a和b值,从而优化ATO系统的控制策略,算法主要包括:
(1)定义列车控制器
PBRL算法中将神经网络作为列车控制器,并利用历史运行数据来训练神经网络。神经网络的输入是列车当前的状态,包括列车当前速度、列车位置和剩余运行时间。输出为下一对牵引-惰行组合工况的控制策略,即下一次采取牵引-惰行时,采用某个a和某个b值的概率。定义列车控制器的神经网络一般结构示意见图2。其中上标1,2,…,J分别代表输出层的节点。
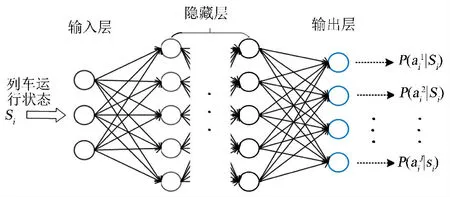
图2 神经网络一般结构示意
(2)评估控制器性能
评估当前控制器的性能也是产生控制器参数更新值的基础。其中,控制策略的累计奖赏值反映了每个控制动作对控制器性能的影响。本文定义动作ai为1个相应牵引-惰行准确的a和b值。
因此列车在站间的控制策略轨迹τ可表示成

式中:si为策略轨迹中第i步时的列车运行状态;ai为第i步时列车的控制动作;ri为在第i步采取动作ai后所得奖赏值。
该控制策略轨迹的累积奖赏值为
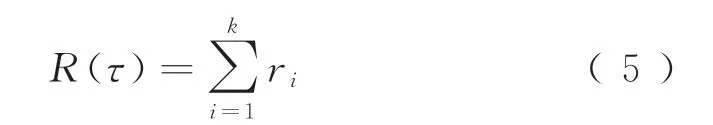
每一步的奖赏值ri为
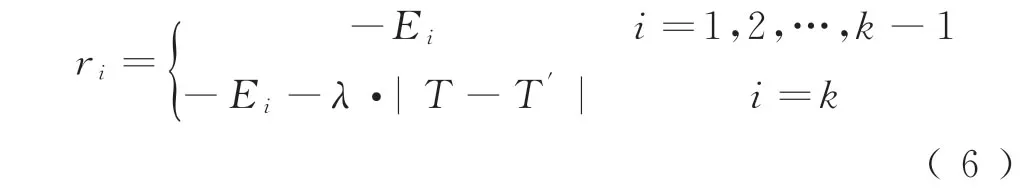
式中:Ei为每一步能耗,可用式(2)计算得到;λ为权重系数。需注意的是,由于专家系统保证了ATO系统的乘客舒适度,因此在奖赏函数中仅考虑能耗和准时性。为计算累计奖赏的期望值,利用当前控制器控制列车运行N次,通过求N次控制策略轨迹的平均累计奖赏来近似期望累积奖赏,即
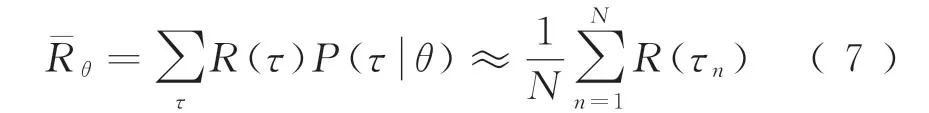
(3)更新参数,获得最佳控制器
训练神经网络的目的是得到一组最大化期望累积奖赏参数
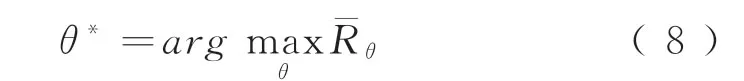
PBRL算法利用策略梯度法来更新神经网络的参数θ,以优化列车控制器。期望累积奖赏的梯度为
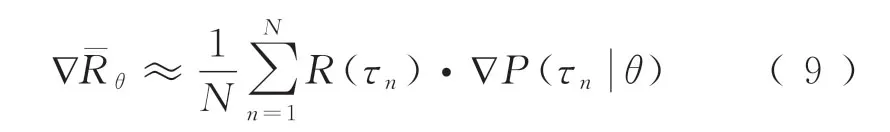
将列车站间的控制策略视为k步决策过程,其条件概率项为
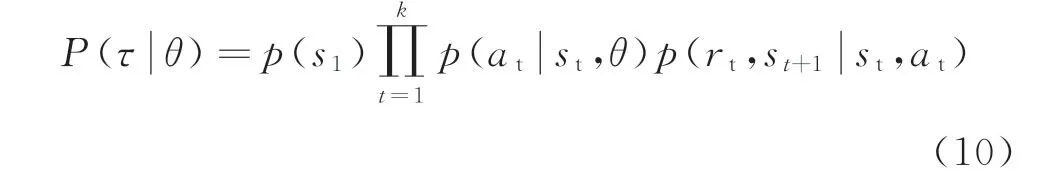
由于式(10)中的p(s1)和p(rt,st+1|st,at)与控制器参数无关,对式(10)求梯度可得
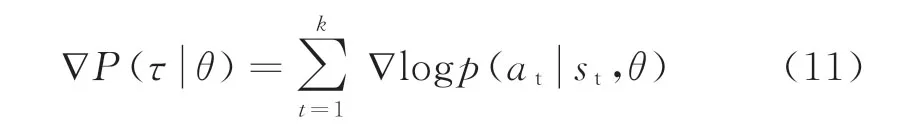
将式(11)代入式(9)可得
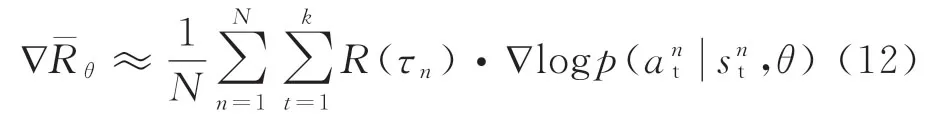
式中:snt、ant分别为控制策略轨迹τn中第t步的状态和控制动作。
最后,根据策略梯度法的更新规则对神经网络参数进行更新

式中:θold、θnew分别为更新前、后的参数。
综上,PBRL算法的具体步骤为:
Step1给定神经网络参数θ,将其作为列车控制器,控制列车运行N次,产生N条控制策略轨迹。
Step2采集这N条轨迹中每一步的运行数据。
Step3利用式(6)计算每条控制轨策略的累积奖赏。
Step4利用式(13)更新控制器参数,产生一个新的控制器。
Step5返回Step1,重复上述步骤,终止满足收敛条件。
3 算例验证与分析
结合北京地铁亦庄线的基础数据进行仿真实验,验证列车节能控制方法的有效性。亦庄线的列车为6节车厢,采用3动3拖的编组形式,总长114 m,净质量为192 t。列车的牵引制动特性和运行阻力特性见文献[24]。
3.1 仿真实验1
在本仿真实验中,通过将PBRL算法计算得到的能耗与现有ATO控制算法进行比较,验证PBRL算法的节能效果。将两种算法的列车计划运行时间均设为125 s,PBRL算法和现有ATO算法计算得到的列车运行速度曲线见图3。从图3可见,现有ATO算法使用的是“减2减5”的控制策略,即:限速为80km/h,当列车速度达到78km/h时,列车惰行;当减速至75km/h时,列车实施牵引工况加速运行。根据在仿真中列车运行时间的计时,其实际运行时间为125.07 s,根据公式(2)计算,列车牵引能耗为24.98 k W·h。利用PBRL算法得到的控制策略则更加灵活,其实际运行时间为124.99 s,能耗为23.27 k W·h。结果显示PBRL算法比现有ATO算法节能6.85%。
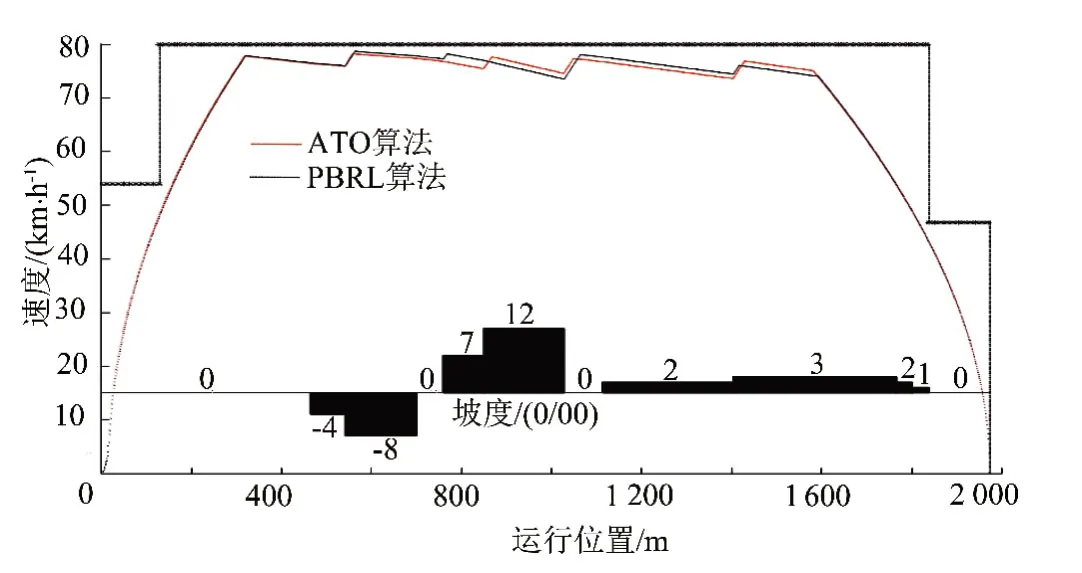
图3 PBRL算法与现有ATO算法的运行速度曲线
在不同计划运行时间下,比较了PBRL 与现有ATO算法和传统ATO算法的准时性、能耗和舒适度性能。仿真结果见表1,为了对表中数据进行更直观地比较,可用(100-PDE)×100%表示乘客舒适满意度,(et/T)×100%表示列车运行误点率。由表1第4列数据计算,传统ATO算法在125、129、132 s三个计划运行时间下平均的乘客舒适满意度为75.3%,而PBRL方法和现有ATO算法的平均乘客舒适满意度分别为100%和99.3%。因此与传统的ATO控制算法相比,PBRL 方法和现有ATO算法在乘客舒适度方面有了很大的改进。更进一步,由表1第2列数据计算,现有ATO算法在125、129、132 s三个计划运行时间下根据列车运行误点率公式计算,平均的列车运行误点率为0.1%,而PBRL 方法的平均列车误点率为(0.01/3)%。相较于现有ATO算法,PBRL方法的误点率降低了30倍,列车运行的准时性大大提高。综上所述,PBRL方法在舒适度和准时性两方面具有明显的性能优势。
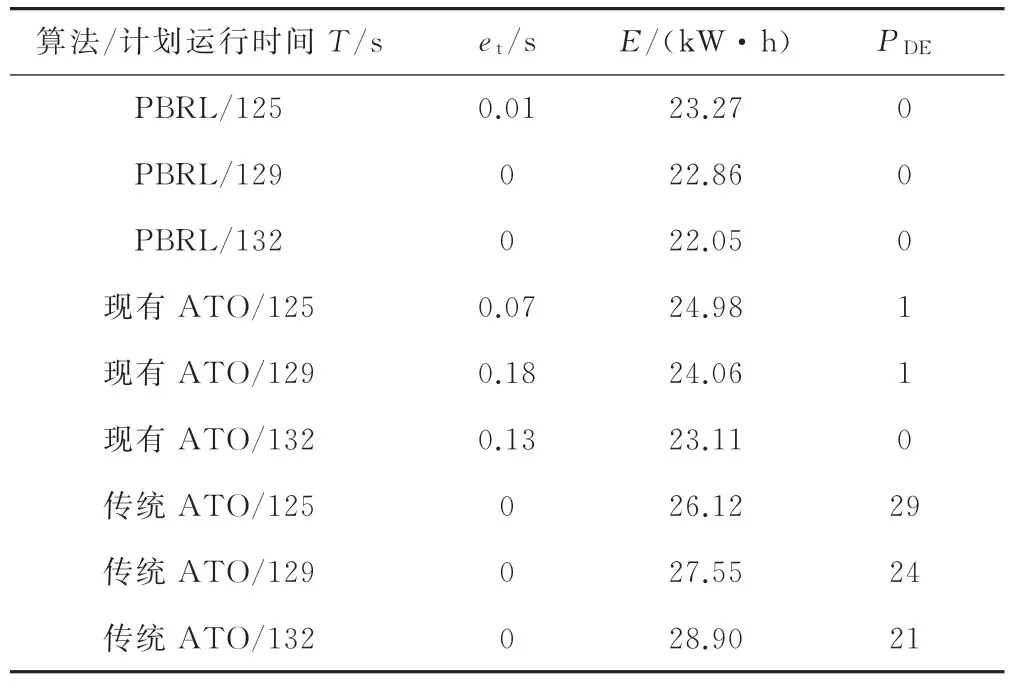
表1 PBRL算法与现有/传统ATO算法的性能比较
3.2 仿真实验2
本仿真实验在不改变其他条件的情况下,将仿真实验1中的运行阻力增大50%,验证PBRL算法在处理可变参数方面的鲁棒性。利用PBRL算法和现有ATO算法求解得到的列车运行速度曲线见图4。由图4可见,现有ATO算法仍然采用“减2减5”的控制策略,但由于运行阻力增大,列车平均运行速度变小,因此,根据在仿真中列车运行时间的计时,其实际运行时间增加到125.67 s,根据式(2)计算,运行能耗为25.43 k W·h。而PBRL算法的实际运行时间为125 s,能耗为23.37 k W·h。实验结果表明:PBRL算法可以根据列车的运行状态来调整控制策略,而不是使用固定的控制策略。即使在随机场景中,依然可以使列车按照计划时间运行,并尽可能地降低牵引能耗。
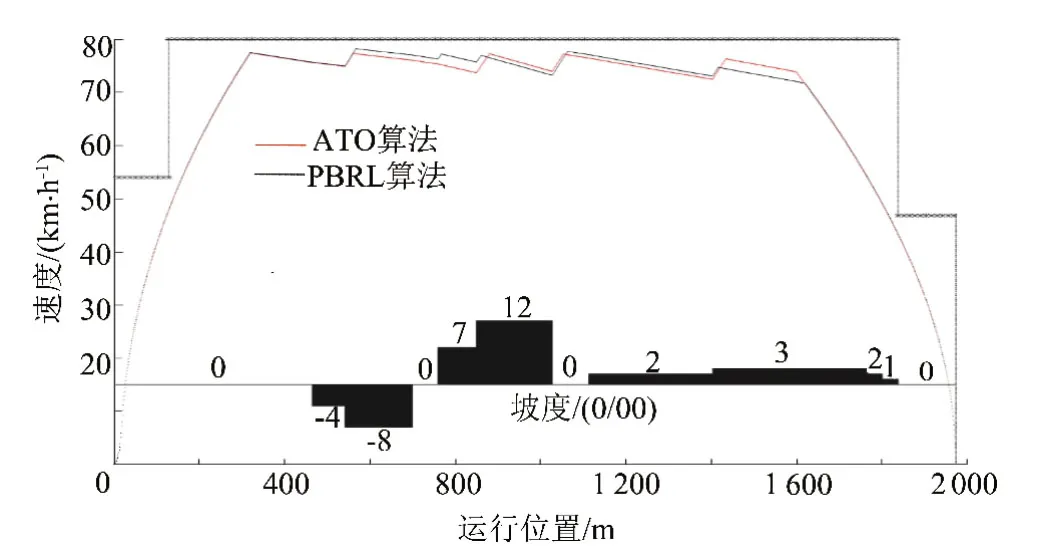
图4 增大运行阻力后两种算法的节能控制策略
3.3 仿真实验3
本次仿真实验通过改变PBRL算法中神经网络隐藏层的神经元个数和式(6)中权重系数λ,分别研究了神经网络结构变化和奖赏函数中权重系数对智能控制器性能的影响。本实验给定的列车计划运行时间为120 s,当隐藏层神经元个数num_h分别为16、32、48和λ取50、100、300时,列车运行的准时性和列车牵引能耗E的结果见表2。由表2可见,当λ取值一定,隐藏层神经元个数num_h=16时,控制器在准时和节能两方面的性能最优。例如,当λ=300时,num_h=16控制器比num_h=48控制器的准时性提高了近1 s,能耗则降低了1.1 k W·h。当λ取值越小,则控制器的平均准时性越好。原因是当奖赏函数中λ越小,在控制器的学习训练过程中会越注重减小列车实际运行时间与计划运行时间的误差,从而保证了列车运行控制过程中的准时性,所以表2中准时性最好的参数设置为λ=50,num_h=16。而当λ越大时,会更注重控制器的节能效果,因此表中牵引能耗最小的参数设置为λ=300,num_h=16。
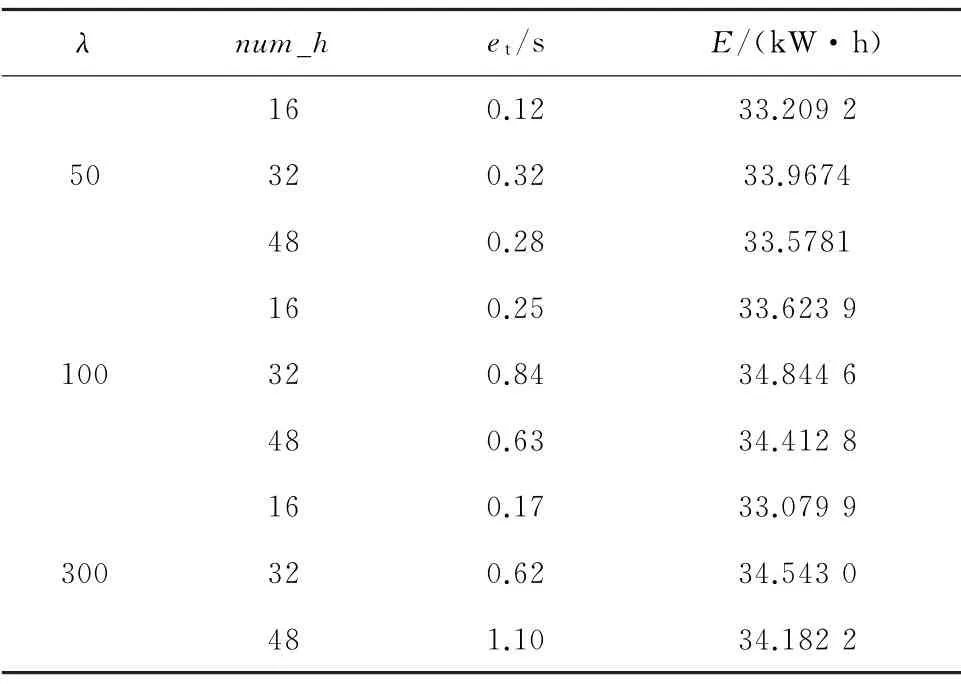
表2 不同num_h和λ 取值时的性能比较
4 结束语
本文建立了列车控制的专家系统,在此基础上提出了基于策略强化学习的列车智能控制算法。一方面,该控制算法能在满足准时性和乘客舒适度的前提下,有效地减少列车牵引能耗,仿真结果表明该算法比现有ATO算法节能6.85%;另一方面,当模型参数发生变化时,该算法仍能保证列车准点运行,具备良好的鲁棒性能。本文所提出的列车智能控制算法集成了现有ATO系统的控制原理和先进的人工智能方法,在实际列车运行控制系统中具有相当的应用潜力。

