高速列车牵引传动系统仿真可信度评估方法

李 晟 彭小奇 彭 涛 阳春华

(1.中南大学 自动化学院,湖南 长沙 410083;2.江西理工大学 理学院,江西 赣州 341000;3.湖南第一师范学院 信息科学与工程学院,湖南 长沙 410205)

我国高速铁路发展迅速,形成了具有中国特色的高铁技术体系。牵引传动系统是高速列车的关键系统[1],其能否稳定可靠工作是确保高速列车运行安全的关键。目前高速列车牵引传动系统的应用验证多采取虚拟仿真或半实物仿真方法,其结果能否正确反映实际系统的性能,取决于仿真系统的可信度,未经可信度评估的仿真系统没有任何价值[2]。但长久以来,仿真可信度问题并没有获得足够的关注[3-4]。

近年来,许多学者对高速列车牵引传动系统仿真进行了研究。西南交通大学、北京交通大学的学者针对CRH 高速列车牵引传动系统,利用MATLAB 搭建虚拟仿真系统或基于dSPACE 搭建半实物仿真平台,通过仿真着重分析牵引时传动电机电磁转矩、三相电流、直流环节支撑电容电压和列车行驶速度的变化情况[5-7]。文献[8]以我国典型高速列车CRH2型动车组为例,通过仿真模型分析牵引传动系统在不同线路条件下的运行情况。文献[9]提出了基于HLARTI和反射内存网的混合网络系统构架的CRH2型高速列车牵引传动系统仿真平台。但目前的文献多数未对其搭建的仿真系统的可信度进行讨论,或仅通过对仿真波形和实测波形进行目测对比来定性分析,而没有给出客观的评估结果。文献[10]提出了一种改进的模糊层次分析法(Fuzzy AHP,FAHP),针对列车运行控制系统仿真进行可信度评估,该方法考虑了评估者对复杂系统判断的模糊性,给出了可信度指标权重确定方法。FAHP能更好地克服人为主观判别、偏颇对决策结果的不利影响,但并未给出可信度指标的具体量化方法且并不适用于牵引传动系统仿真。由文献检索可知,在高速列车仿真领域目前还缺乏针对牵引传动系统仿真的可信度评估理论体系。如何给出适用于高速列车牵引传动系统仿真信号特点的可信度指标量化模型,如何利用评估专家的宝贵经验确定可信度指标的权重并尽可能降低主观偏好带来的不利影响,是急待解决的关键问题。

本文针对牵引工况下,在理想情况即平直道路上运行时的高速列车牵引传动仿真系统,提出一种新的仿真可信度评估方法。该方法首先根据信号的缓变特性,利用残差相似度构造指标的整体可信度;再根据信号的瞬变特性,利用基于SVD-TLS算法改进的Prony分析采集信号的频率、幅值和阻尼特征量,根据相似性原理利用各特征量构造指标的特征可信度;通过综合整体可信度和特征可信度给出可信度指标的量化模型。其次,使用群组AHP 方法确定可信度指标的权重,有效降低了主观偏好的不利影响。最终,给出仿真可信度的综合量化模型,形成一套完整的仿真可信度理论体系。将此方法应用到CRH2型动车组牵引传动系统的无故障仿真和故障注入仿真实验的可信度评估过程中,准确客观地评估了仿真结果的可信度;并将可信度评估结果用于仿真模型关键参数的修正,为参数修正提供了客观的数据支持。实践表明,本文所提方法是有效、合理的。

1 高速列车牵引传动仿真系统简介

高速列车牵引传动系统一般由单相三电平脉冲整流器、直流环节支撑电容、三电平逆变器和牵引电机组成的牵引传动系统主电路和牵引控制器组成。牵引控制器接收车载传感器反馈信号,按给定的控制策略输出控制指令,控制脉冲整流器、逆变器等,总体思路见图1,仿真所涉及的电气设备电气参数均参考文献[1]和文献[6]中的数据设置。

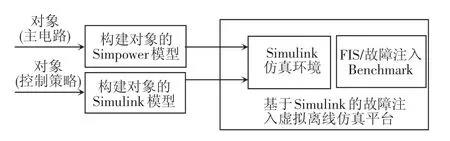
图1 基于Simulink牵引传统系统虚拟离线故障注入仿真平台总体思路

基于Simulink的牵引传动系统故障注入/模拟Benchmark框架见图2。由故障注入基准库、故障注入模块和故障注入控制器组成,采用修改信号和变量/参数的方式,完成牵引传动控制系统各故障模式的注入、仿真/模拟。其中,故障注入基准库提供所有故障的属性信息(包括故障模式及故障数学描述等);故障注入模块是根据已实现子系统中各故障类型的模拟方案,在Simulink环境下搭建出的故障注入模块库,包括变流器、控制器TCU、传感器、牵引电机4个部分的故障注入模块;故障注入控制器用于控制及实现具体故障信号的注入、仿真/模拟。

根据实际车载传感器的分布,通常选择电磁转矩、三相电流、直流环节支撑电容电压和列车行驶速度等作为反映仿真可信度的观测信号[6]。这些信号各具特点,但均包含了缓变和瞬变信号的特征,尤其在故障注入时,瞬变信号的特征显得尤为重要。因此在进行仿真可信度评估时,应同时考虑缓变信号和瞬变信号的特征提取。

2 仿真可信度评估方法

2.1 可信度指标的量化模型

2.1.1 基于残差分析的整体可信度

残差时序向量是将仿真信号时序向量与实测信号时序向量相减后得到的,它很好地反映了信号的整体误差和缓变信号特征,据此可建立可信度指标的量化模型

图2 基于Simulink的牵引传动系统故障注入/模拟Benchmark框架

式中:xi、分别为实测信号、仿真信号幅值序列的第i个幅值;n是幅值序列的维数;σi为第i个点的可信度;αi为第i个点的重要程度;CE为仿真信号与实测信号的残差可信度量化指标,称为残差相似度。易证明,σi关于单调递减,因此CE也满足单调性。残差相似度作为2个时间序列间的距离,是一种静态度量,体现了信号的整体误差水平,因此定义CE为可信度指标的整体可信度。由于仅通过CE难以区分信号间不同瞬变性能的误差,因此还需对信号误差进行进一步分析,以提取信号的瞬变特征。

2.1.2 基于特征分析的特征可信度

特征值分析法的思路是比较仿真信号和实测信号的各特征值间的差异,通过这些差异来计算信号间的误差。Prony分析可以提取信号的频率、幅值、阻尼和能量等特征,它是用一组指数函数的线性组合来拟合等间隔采样数据。Prony分析提取的特征量可以很好地表征信号的瞬变特性,故被广泛应用于低频振荡分析、模态识别和雷达信号分析等领域[11-13]。

本文选取信号频率、幅值和阻尼3个特征,构建频率相似度、幅值相似度和阻尼相似度3个参量来表征信号瞬态特征的误差。先给出信号的能量表达式,设n为采样点数为采样点幅值,则离散信号的能量公式为

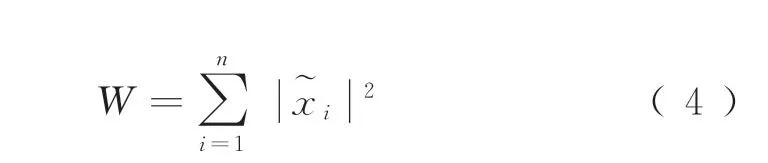
通过Prony分析,提取实测信号和仿真信号的频率、能量向量对分别为

式中:FM、FS分别为实测信号和仿真信号的频率、能量向量对;fMi、fSi分别为实测信号和仿真信号频率向量的第i个频率分量;WMi、WSi分别为实测信号和仿真信号能量向量的第i个能量分量。通常n1≠n2,且n1和n2均较大,故采用以下方法降维并统一维数。方法步骤如下:

Step1将能量小于总能量0.1%的信号分量删除,并按照能量从小到大的顺序将剩余分量重新排序,获得新的频率、能量向量对

实验表明:n3、n4远小于n1、n2。f′Mi和f′Si分别为降维并统一维数后实测信号和仿真信号频率向量的第i个频率分量;W′Mi和W′Si分别为降维并统一维数后实测信号和仿真信号能量向量的第i个能量分量。

Step2生成新的频率、能量向量对F″S。其生成规则是:F″S中第i个元素为F′S与F′M中第i个元素相距最近的元素。距离计算式为

式中:dij为F′S中第i个元素到F′M中第j个元素的距离;χ为可以根据具体信号调整的常数;a′Mi、a′Sj为对应频率的幅值。

通过以上步骤,向量F″S与F′M维数一致,频率相似度为式中:f′Mi、f″Si分别为实测信号与仿真信号中第i个点的频率;σfi为第i个点的可信度;W′i表示降维并统一维数后第i个点的能量;βi为第i个点的权重;CF为频率相似度。因非周期信号频率为零,故在频率相似度的计算中不予考虑。

类似可以给出幅值相似度的定义。在得到维数一致的2个幅值、能量向量对A″S、A′M后,幅值相似度为

式中:a′Mi、a″Si分别为实测信号与仿真信号中第i个点的幅值;σAi为第i个点的可信度;γi为第i个点的权重,计算式同式(10);CA为幅值相似度。

同理,得到维数一致的2个阻尼、能量向量对D″S、D′M,相应的阻尼相似度计算式为

式中:d′Mi、d″Si分别为实测信号与仿真信号中第i个点的阻尼因子;d′Mid″Si＜0为信号衰减趋势完全相反,故相似度为0;σdi为第i个点的相似度,其计算式同式(10);δi为第i个点的权重;CD为阻尼相似度。幅值相似度和阻尼相似度的计算均应考虑非周期分量信号。

由于频率、幅值和阻尼相似度均源自于信号特征,可以认为3者具有同等重要性,即其权重应相同,故定义表征信号瞬变特性的特征可信度CT为

综合考虑整体可信度和特征可信度所构建的仿真可信度评估指标的可信度量化模型为

式中:0≤λ≤1。λ越大,表示越重视信号缓变特征对可信度指标量化的影响;λ越小,表示越重视信号瞬变特征对可信度指标量化的影响。

2.2 基于群组AHP的指标权重确定方法

在仿真可信度评估过程中,仅依靠误差分析,会丢失专家经验中的有用信息,但评估专家的判断又受其学术水平、工作经历以及对待评对象的熟谙程度等主观因素的影响。为此,本文引入群组AHP 方法来确定各可信度评估指标的权重,以便既吸收专家的宝贵经验,又使评估结果更加客观合理。

群组AHP 方法(Group AHP)[14]是由多位专家运用AHP法对待评对象进行分析,然后再对各专家的判断矩阵进行聚合,得到综合判断矩阵,从而形成更加客观合理的群组评估结果。其核心问题是专家权重的确定和综合判断矩阵的一致性分析。

邀请m位待评仿真系统相关领域的专家组成评估专家集合E={e1,e2,…,em},第k位专家的权重用ηk表示。针对待评仿真系统,每位专家按照AHP的1-9标度设置方法,给出相应的判断矩阵Ak=(akij)l×l(k=1,2,…,m),其中l表示AHP方法中同层可信度指标数。对所有判断矩阵进行一致性检验,使一致性比例CR小于0.1,经专家反复调整,直到所有判断矩阵都通过一致性检验为止[15]。CR的表达式为

式中:n为判断矩阵的阶数;λmax为判断矩阵的最大特征值;RI是可通过查表得到的平均随机一致性指标。

判断矩阵的一致性水平是专家评判可靠性和严谨程度的体现。CR越小,判断矩阵的可靠程度越高,相应专家的判断重要程度越高;CR越大,表明判断矩阵的可靠性低,相应评估专家的判断重要程度降低。因此评估专家权重为

由于CRk＜0.1才能通过一致性检验,故μ取10较为合适。

群组AHP方法的另一个关键问题是将所有评估专家的判断矩阵进行集结,得到包含所有专家判断信息的综合判断矩阵,该矩阵也要通过一致性检验。文献[16]已证明,若A1,A2,…,Am为m个专家给出的判断矩阵且均为一致性可接受判断矩阵,则其加权几何平均综合判断矩阵也是一致性可接受矩阵。由此定义综合判断矩阵为

式中:◦为加权几何平均集结算子。

设l为同层可信度指标数,则上述矩阵元素的计算式为

可以求得归一化的可信度评估指标的综合权重向量ω=[ω1,ω2,…,ωl]。其中,ωi表示该层第i个可信度指标的综合权重。

2.3 仿真系统可信度评估方法

本文提出的仿真系统可信度评估方法见图3。

图3 仿真系统可信度评估方法体系框

设Ci是根据式(18)获取的该层第i个可信度量化值,则基于信号误差分析和群组AHP 方法的仿真可信度评估量化模型为

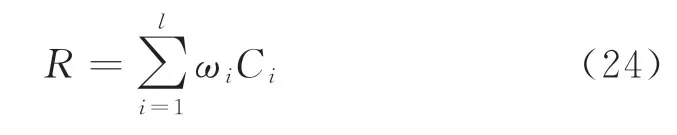
3 仿真实验与可信度评估算例

由于无法获取CRH2型动车组牵引传动控制系统实际信号的录波数据,本文利用dSPACE 仿真器和实物控制器搭建图4所示的系统半实物实时仿真平台进行半实物仿真,并以基于该平台的仿真结果作为参照的实测数据。

图4 基于dSPACE的高速列车组牵引传统系统半实物实时仿真平台实现总体思路

3.1 Prony分析阶数确定

在利用Prony进行信号分析时,阶数选择对分析的结果有较大的影响,甚至导致所提取的特征信息严重失真,无法用于可信度评估。故提取特征信息前须确定合理的阶数。

影响阶数选择的指标主要有:动态变化率DVR和信噪比SNR[17]。DVR反映了重构数据与实测数据的整体误差大小,DVR越低,重构数据与实测数据越吻合。而SNR越大,表示Prony估计的精度越高。

文献[18]指出,Prony分析在实际应用中取能使SNR达到40 dB且DVR小于1%的阶数,即可满足运行时间和精度要求。为得到满足2个指标的阶数,本文采用奇异值-总体最小二乘法(Singular Value Decomposed-Total Least Square,SVD-TLS)对原始信号进行去噪并确定Prony分析的阶数[19],再使用Prony算法提取信号特征。

3.2 无故障仿真算例

分别在基于Simulink的虚拟离线仿真平台和基于dSPACE的半实物实时仿真平台上进行无故障仿真。采样间隔3×10-3s,时长10 s。仿真结果见图5。通过目测法定性对比逆变器a相电流、列车行驶速度、牵引电机电磁转矩、直流环节上支撑电容电压4个观测点的信号可见,两者的仿真结果很接近。但定性分析的结果并不客观,还需要进行定量的客观分析。

图5 Simulink和dSPACE仿真结果对比

以逆变器a相电流信号的重构为例,由SVD-TLS算法确定的Prony分析阶数为58时,原信号与重构信号波形见图6,两者几乎重合,此时SNR=41.983 4,DVR=0.006 33,符合精度要求。可见,本文采用的基于SVD-TLS算法改进的Prony分析所得到的频率、幅值、阻尼因子和能量向量是有效的。

采用本文所提出的相似度量化公式分别求各相似度的量化值,结果见表1。

图6 原始信号与Prony重构信号比较

表1 无故障仿真各相似度量化值 %

由于是无故障仿真,故可以认为整体可信度和特征可信度的重要性相同。令式(18)中的λ=0.5,利用式(17)、式(18)分别计算各可信度指标的可信度量化值,可得:逆变器a相电流可信度C1=91.54%,列车行驶速度可信度C2=96.83%,牵引电机电磁转矩可信度C3=94.34%,直流环节上支撑电容电压可信度C4=95.29%。

邀请4位相关领域内专家组成仿真可信度评估专家集合E={e1,e2,e3,e4},每位专家按照AHP 方法将逆变器a相电流、列车行驶速度、牵引电机电磁转矩、直流环节上支撑电容电压4个可信度指标进行两两间的重要性比较,按照1-9标度法分别给出4个判断矩阵

分别对4个判断矩阵进行一致性检验,由式(19)、式(20)可以得到一致性比例CR,分别为CR1=0.005 4,CR2=0.027 3,CR3=0.044 0,CR4=0.017 8,均小于0.1,故4个判断矩阵均为一致性可接受矩阵。取μ=10,利用式(21)可以确定专家权重η分别为η1=0.289 5,η2=0.239 7,η3=0.211 9,η4=0.259 0。

利用式(22)、式(23)计算可得综合判断矩阵A为

计算一致性比例CR=1.015 2×10-4,远小于0.1,且有CR＜CRi(i=1,2,3,4)。可见群组AHP方法所获得的权重比AHP 方法获得的权重更加客观准确,有效降低了主观意志的影响。

根据综合判断矩阵,采用特征值法可以求得可信度评估指标的综合权重为

根据式(24)可得基于Simulink的CRH2高速列车组牵引传动系统仿真综合可信度为

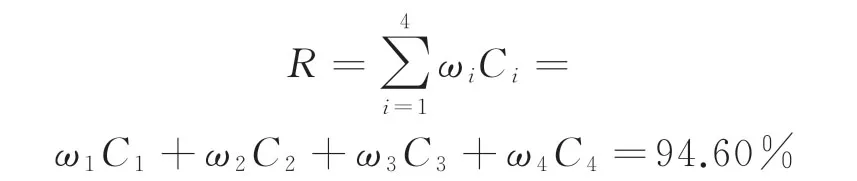
仿真综合可信度的分析计算结果非常接近100%,表明基于Simulink的仿真系统与作为参照的dSPACE仿真系统的仿真结果一致。

上述结果表明,本文提出的仿真可信度指标合理有效,通过群组AHP 方法确定权重能吸收评估专家的宝贵经验,使可信度指标权重更加客观合理;同时也证明,基于Simulink的虚拟离线仿真系统的仿真结果是可信的,该仿真系统模型是准确有效的。

3.3 实际故障仿真算例

3.3.1 故障注入仿真实验

牵引变流器是牵引传动系统的动力源和能量转换核心设备,一旦发生故障,将使列车运行在不稳定状态,严重时将导致列车丧失动力,被迫停驶。2007年5月28日CRH2型012A 动车组7车主断路器断开,复位后故障未消除,经查是牵引变流器发生故障,因此采取切除8车牵引变流器、保留75%动力维持运行。下载故障数据,并通过厂家专用分析软件对其进行分析,确定逆变单元IGBT 模块内部U 相上桥臂2号功率器件短路是导致该故障的真正原因。采用基于Simulink的虚拟仿真系统对这次故障进行仿真。设定故障严重程度因子为0.95,故障注入时间3 s,选择中间电路上下支撑电容电压,以及列车行驶速度和电磁磁矩的仿真结果与实际录波进行对比(见图7),仿真波形与实录波形变化趋势基本一致,局部存在差别,表明通过故障注入仿真实验可以较为成功地复现实际故障。

图7 Simulink故障仿真结果和实录波形结果对比

3.3.2 仿真结果可信度分析

为客观评估仿真结果与实际故障间的差异,并借助可信度来修正仿真模型的关键参数,以提高仿真的准确度,利用本文提出方法定量分析仿真结果与实际故障间的差异。当故障严重程度因子设置为0.95时,各可信度指标的量化值见表2。

表2 IGBT 短路故障各相似度量化值(故障严重程度因子0.95) %

4位评估专家给出的判断矩阵如下

取μ=10,利用式(21)计算得到专家权重为

由式(22)、式(23)得到综合判断矩阵为

用特征值法求得基于群组AHP的可信度评估指标的综合权重分别为:直流环节上支撑电容电压ω1=0.238 5,下支撑电容电压ω2=0.253 8,列车行驶速度ω3=0.314 9,牵引电机电磁转矩ω4=0.192 8。由式(17)、式(18)分别计算各可信度指标的可信度综合量化值,可得:直流环节上支撑电容电压可信度C1=85.92%,下支撑电容电压可信度C2=84.24%,列车行驶速度可信度C3=99.72%,牵引电机电磁转矩可信度C4=85.57%。

因故障状态下,瞬变特征比缓变特征更为重要,故取式(18)中的λ=0.3,最后由式(24)计算得到基于Simulink 虚拟故障注入仿真系统的综合可信度为R0.95=89.77%。

由计算结果可见,本次故障注入仿真的可信度较高,仿真波形与实际波形吻合较好,定性分析和定量分析结果一致。可见,利用本文提出的方法得到的仿真可信度评估结果是正确有效的。

3.3.3 基于可信度的仿真模型关键参数修正

仿真模型关键参数的设置不同,会导致仿真结果间存在差异。关键参数设置的不合理,甚至会导致仿真结果的严重失真。通过定性比较来修正模型参数的难度和主观性较大,而利用本文所提出的仿真可信度计算方法,可通过不同的关键参数设置计算出对应的仿真可信度量化值,将其作为修改关键参数的客观依据。以故障注入仿真实验时,故障模型中的故障严重程度因子这一关键参数的选择为例,验证本文方法能够对模型关键参数的修正提供指导。

在IGBT 短路或开路故障仿真中,故障严重程度因子多采用经验设定,主观性很大,也无法判断该参数设定值的优劣。为此,设置故障严重程度因子分别为0.95、0.90、0.85,并进行故障注入仿真。IGBT 短路故障会影响列车的平稳运行,对列车速度的影响较为明显。通过与CRH2型动车组上速度传感器采集的故障数据进行对比,得到列车速度的仿真波形与实际波形,见图8。由图8可以看到,故障严重程度因子分别为0.95、0.90、0.85时,仿真波形与实录波形变化趋势基本一致,通过定性分析无法得知哪个参数更为合理。

图8 不同参数时Simulink故障仿真结果和实录波形结果对比

表3、表4列出了故障严重程度因子为0.90和0.85时对应的相似度量化值,计算可得综合可信度量化值分别为R0.90=90.94%,R0.85=86.90%。可见,当故障严重程度因子设定为0.90时,仿真综合可信度最高,且各相似度量化值也不同程度的高于0.95和0.85。因此,选择故障严重程度因子为0.90更加准确合理。

表3 IGBT 短路故障各相似度量化值(故障严重程度因子0.90) %

表4 IGBT 短路故障各相似度量化值(故障严重程度因子0.85) %

4 结论

(1)提出了一套完整的仿真可信度评估方法。提出了仿真的整体可信度的概念,通过残差分析来构造整体可信度量化模型;提出了仿真的特征可信度的概念,通过Prony分析提取信号特征量,并通过提取的特征量构造特征可信度量化模型;将整体可信度和特征可信度相结合,得到各可信度指标的可信度量化模型;基于群组AHP 方法确定各可信度指标的权重,有效降低了确定权重过程中的主观性,在吸收专家经验的同时,使评估结果更加科学合理;通过SVD-TLS算法确定Prony分析的阶数,使特征可信度的计算准确可靠。

(2)将虚拟离线仿真系统的仿真结果分别与基于dSPACE的半实物实时仿真系统的数据和实际发生的某次故障的数据进行对比。实例表明,利用本文所提出的方法可以计算仿真系统的综合可信度量化值,从而客观的对仿真结果的准确性进行评估。

(3)依据综合可信度量化值在不同仿真模型关键参数设置下的计算结果,可对仿真模型的关键参数进行修正,进一步提高仿真的准确度。