道路工程SOM-RBF神经网络估价模型研究
段晓晨 徐 佳
(1.石家庄铁道大学 经济管理学院,河北 石家庄 050043;2.山西财贸职业技术学院,山西 太原 030006)
毋庸置疑,道路工程的发展对促进国家经济发展具有重要作用。道路工程投资大,其造价管理工作对于道路工程按时、保质保量完成具有重要意义,但有些工程在开工后出现资金短缺、施工工效低、工程结算困难,影响工程质量或拖延工期等问题。造成这些问题的主要原因之一是项目前期准备工作不够,其中投资估算不准确的问题更为突出。投资估算面临的主要问题是,缺乏有效的估算方法,在有限时间内进行快速而准确的估算。
目前投资估算的主要方法有两类,一类是利用函数对投资进行估算,如单位生产能力估算法、生产能力指数法、比例估算法、系数估算法、综合指标投资估算法等,这些方法用于项目没有具体图纸和工程量清单时,函数应用条件严苛,需要选择相关经验数据,投资估算误差大。另一类是利用定额和造价信息进行分部组合计价,用于项目设计方案确定的情况,这类方法估算精度提高,但计算量大,估算工作繁琐。工程项目本质上是非线性系统,经验丰富的工程人员,可根据工程资料,估算出项目的建设费用、用工数量、主要材料消耗量等,而且经验越丰富,估算越准确。因此,国内外许多学者对模仿人脑神经网络行为特征的神经网络信息处理模型进行了大量研究,探索投资决策阶段准确快速的估价方法。其中研究较为成熟的网络是BP(Back Propagation)网络,并且神经网络可对非线性系统的特征向量聚类的思想被学者提出[1-2]。近年来,RBF(Radial Basis Function)及其改进的网络在相同的条件和输入节点相同时与传统神经网络相比具有效率高和精度高的优点[3-5],RBF网络的研究重点在径向基函数中心的选择。目前径向基函数中心的选择方法主要有随机选择法、有监督学习、正交回归方法、遗传算法、SOM(Self-organization Mapping)学习算法等。其中SOM 可对存在特征向量的类似问题进行聚类,并有学者将SOM网络和RBF网络相结合的模型在地下水位预测[6]、污水处理[7]和过程质量预测[8]等非线性复杂系统预测上进行实证。工程项目虽具有各自特征,但存在类似工程,从项目中提取的特征向量具有高度的自适应性,存在一定规律,符合SOM网络聚类要求。
综上所述,本文从以下方面进行研究。(1)全生命周期造价(Whole Life Cost,WLC):即包括建设期、使用期和翻新与拆除期等阶段总造价最小化的方法[9],指导选择更为科学的建筑设计和更加合理的建筑材料,以实现更为科学合理的投资决策。(2)“显著性理论”(Cost Significant,CS)思想:即抓住并着重解决对整个问题起重要作用的约20%的因素,面对数据繁多的造价信息,既节省了时间和资源,又解决了主要问题。这样,全生命显著性造价理论(Whole Life Costsignificant,WLCS)将WLC和CS相结合可以既全面又有重点的对投资项目进行控制[10-11]。(3)SOM和RBF相结合的神经网络:即通过SOM算法聚类建立RBF预测模型。
1 WLCS模型简介
全生命周期造价WLC确定模型采用NPV 法[3],把项目造价占整个工程项目总造价80%的分项工程称为显著性成本项目(Cost-significant Items,CSIs)。
将CSIs方法运用于WLC中,如下全生命显著性造价(Whole Life Cost-significant,WLCS)计算公式
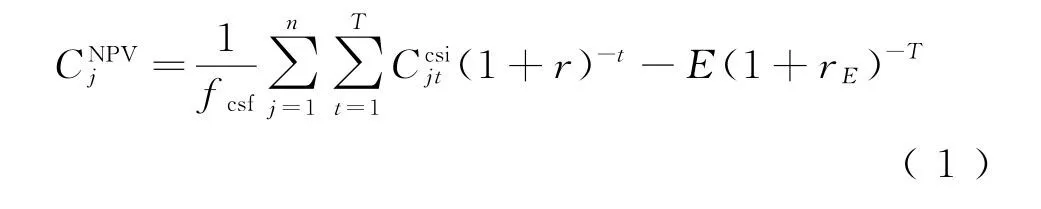
式中:Ccsijt为备选方案j建造成本、运营和养护成本的显著性项目;T为整个项目全生命分析期;r为期望年折现率;E为弃置收益减去弃置成本的净值;rE为弃置净值的折现率;fcsf为显著性因子;n为显著性成本项目的数目;CNPVj为备选方案j全生命周期造价的现值之和[12-13]。
2 SOM-RBF的WLCS模型
考虑一个由N维输入空间到一维输出的映射。设N维空间有M个输入向量Xp,p=1,2,…,M,它们在输出空间相应的目标值为dp,M对输入输出样本构成了训练样本集。插值的目的是寻找一个非线性映射函数F(X),满足插值条件为

函数F描述了一个插值曲面,该插值曲面必须通过所有训练数据点。解决方法为,选择M个基函数,每个基函数对应一个训练数据,各基函数的形式为
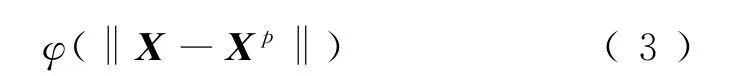
式中:φ为非线性函数;训练数据点Xp是φ的中心。基函数以输入向量X与中心之间Xp的拓扑距离作为自变量[14-16]。
基函数的线性组合为
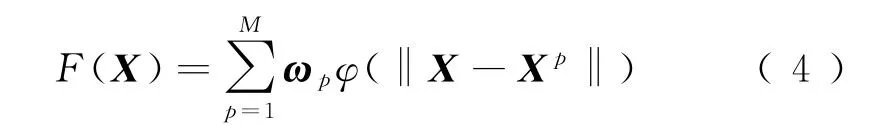
将式(2)的插值条件代入式(4),得到M个关于未知系数的线性方程组[9]

式中:ω、d分别为系数向量和期望输出向量。
式(5)可以改为

式中:Φ为函数φ的解构成的矩阵,若可逆,就可以从式(6)中解出系数向量ω,则

为了保证插值矩阵可逆,Micchelli定理给出如下条件:对于一大类函数,如果X1,X2,…,XP各不相同,则P×P阶插值矩阵可逆。高斯函数就属于这类函数。
(1)网络训练
首先对输入样本数据进行归一化处理,然后通过聚类网络进行无导师学习分类,得到q种类别,即为网络中心的个数,网络隐层各个基函数的中心和宽度也同时被确定。聚类网络的第s个分类中获胜神经元为第s个基函数的中心cs,s=1,2,…,q,获胜神经元的权值向量为基函数中心的宽度。输入层到隐层的映射采用高斯函数,隐层到输出层的连接权值采用最小二乘法确定。
(2)估算预测
分别将CSIs总造价值和fcsf值作为网络输出,即预测值。将特征值输入训练好的网络,运行若干次,对预测的CSIs和fcsf值求均值。

式中:CWLC为工程项目的WLC造价;Ccsi′jt为经RBF网络预测的CSIs造价;fcsf′为预测的fcsf。
对于模型的效果评价从以下两个方面进行:一是对SOM网络聚类评价,二是对估算结果评价,本文选取相对误差作为评价指标,而对于不同样本数的训练,可以用平均相对误差对训练结果进行比较。
3 模型实证
3.1 WLCS模型数据分析
本文是以实际已完工程的公路结算或决算工程量清单为研究对象。论文所用原始数据、资料等主要来源于:关于模型实证所用的工程量清单搜集、从企业或机构的实地调研、获取工程在正常施工条件下结算或竣工决算;关于计算造价时所需基本参数的确定,从行业网站、政府官网及统计年鉴等查询或计算;关于公路工程特征类目量化值的确定所需要专家意见调研,采用德尔菲法。其中德尔菲法调研流程为:以省高速公路管理局和公路工程施工企业高级工程师为专家,将工程资料,包括工程概况、工程合同及工程结算等资料发给专家,同时向专家发出调查问卷,经4轮调研,用统计方法对工程特征类目和类目量化值进行确定。
将高速公路的路基、路面、桥涵及隧道等单位工程分开计算,以路基、路面为例进行实证。选取山西省、广西省、吉林省等已完高速公路工程标段为样本,将样本用阿拉伯数字代替工程具体名称,并随机列表。
样本准备好后,对清单中分项工程成本进行分析,计算单位造价。具体步骤计算为:
Step1建立公共的假设和参数。

表1 某高速公路路基路面WLC的CSIs
Step2将样本的工程结算价折现到同一基准年。
(1)初始化成本。路基和路面分项工程的初始化成本根据工程计量台帐和清单支付报表等计算。得到竣工年份的造价,通过净现值公式计算到t0年。对于仅有合同价的样本,也需考虑风险因素。
例如:A项目工程路基挖石方金额为12.5元/m3,合同工程量为100 m3,变更累计工程量为30 m3,起点桩号为K0+000,止点桩号为K0+020。每米工程量为
(100+30)/20=6.5 m3/m
然后分项工程每米造价为
12.5×6.5=81.25元/m
即路基挖石方单位米的初始成为本为81.25元/m。其中未完工程,按照造价比例,根据汇总表中的暂定金额,计算分项工程的暂定金额,代替变更工程量。
(2)运营和养护成本需按照(1)中的基准年进行折现,包括日常养护,管理费用等,根据票据、记录等资料汇总得到。养护内容按照搜集的数据计算,为了体现CSIs,防止重复计算,并防止混淆CSIs和non-CSIs,养护内容分为两种方法处理:能够和建设成本合并的养护工程,与建设成本中的分项工程一起考虑。不能计算到建设项目分项工程中的,和建设成本中工程量清单中的分项工程一起列出。
(3)修理成本和替换成本不一定每年都发生,同样在折现到基准年价值后计入。
(4)残值。本文假设总成本的残值为0。
Step3计算全生命周期成本。所有成本折现后求和,可以得到全生命周期成本,并计算得到每千米造价。
计算得到以上分项工程生命周期成本基础数据后,用“均值理论”对数据分析,确定CSIs和non-CSIs,如果一次不能满足“显著性”要求,需进行二次平均,求出CSIs 见表1。求和WLC总造价1 444 341元/km,分项工程总数为22,CSIs个数为5。比例为22.7%。除去路面小修保养成本,其余路基和路面的运营和养护成本分别处理。
再次通过均值理论计算WLC 得到CSIs和fcsf,见表2。

表2 某高速公路路基路面CSIs的WLC
经过计算,分项工程总数为17,CSIs个数为4,比例为23.5%。对比发现,分项工程的WLC 可以识别对WLC造价作用明显的运营养护费用,更能体现数据规律。计算后项目CSIs发生了变化,同时fcsf也发生了变化。
3.2 同类工程SOM-RBF聚类分析
列举工程特征的不同类目,依据定额水平及工程特征对造价影响的相关性导致平方米造价的改变,从小到大排序,并根据专家经验给定对应的量化数据,结果见表3。按照工程特征选取15个工程,CSIs计算结果见表4。

表3 已完公路工程特征类目量化表

表4 显著性成本项目(CSIs)计算结果(节选)
(1)CSIs和fcsf确定类似工程
结果表明,工程特征相同的工程,CSIs大致一样,fcsf存在偏差。分析工程概况发现,由于工程规模、具体施工的某段地形、施工情况以及一些不确定的因素,CSIs不完全相同。
一方面,同一工程特征计算得到的CSIs大致相同,fcsf一致,集中在80%~83%之间,存在一定的偏差。另一方面,不同的工程特征下,CSIs项目大致不同,但是fcsf集中在78%~82%之间。综上,显著性理论在工程造价中是存在的,验证了同一工程特征下,CSIs大致相同并且fcsf大致相同的工程为同类工程。
(2)SOM-RBF对类似工程验证
SOM-RBF网络聚类分为训练和测试两个过程,利用同一工程特征下,CSIs相同并且fcsf相同的工程为同类工程这一条件作为训练标准,检验网络对工程特征聚类是否可行。
将CSIs和fcsf构成的向量作为网络的输入向量,将用fcsf数值化后的CSIs通过网络映射到低维空间后,由网络生成的聚类可以检验WLCS的CSIs和fcsf对类似工程的确定。训练样本共15个输入向量,每个向量分量用CSIs占总造价的比值表示。选取参数,学习率的初始数为100、500、1 000,对训练结果进行比较。训练过程见图1,聚类结果见表5。将样本CSIs的相似度以及fcsf误差范围作为判断标准。计算样本CSIs的相似度αi为
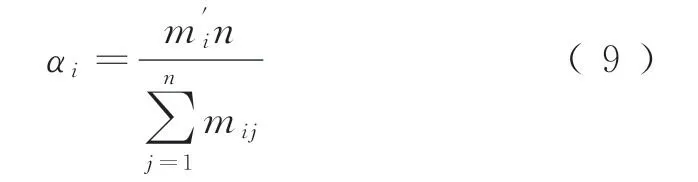
式中:i为类别,i=A,B,C;n为某聚类中样本个数;mij为某聚类中某个样本的CSIs个数;m′i为每个聚类中相同的CSIs个数。
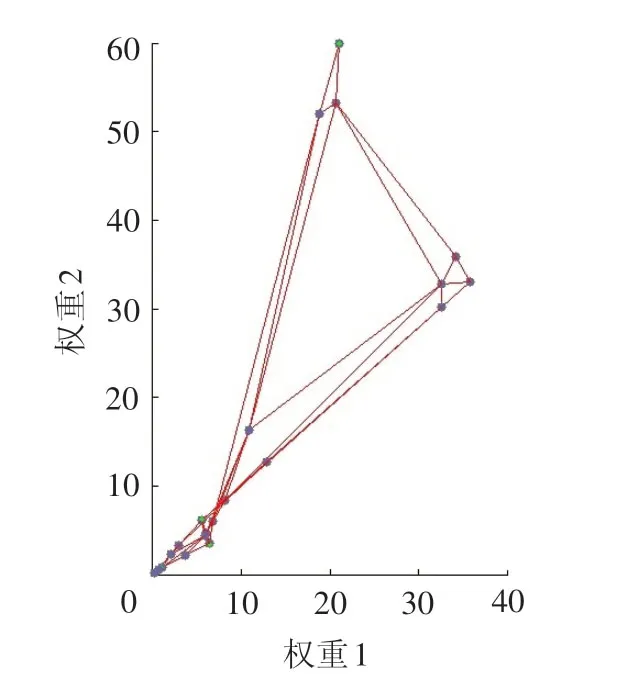
图1 SOM-RBF训练过程的状态
当训练步数为100时,网络对于样本初步分3类,与“同一工程特征下,CSIs大致相同并且fcsf大致相同的工程为同类工程”的判断相符。类别A的αA为83.33%,同理计算得αB=78.9%和αC=75%,取均值后,样本CSIs的相似度为79%,网络运行结果表明fcsf偏差在±3%内为同类或类似工程。当训练步数为500时,SOM网络分类细化,计算CSIs的相似度为83.33%,fcsf偏差在±2.25%内为同类或类似工程。
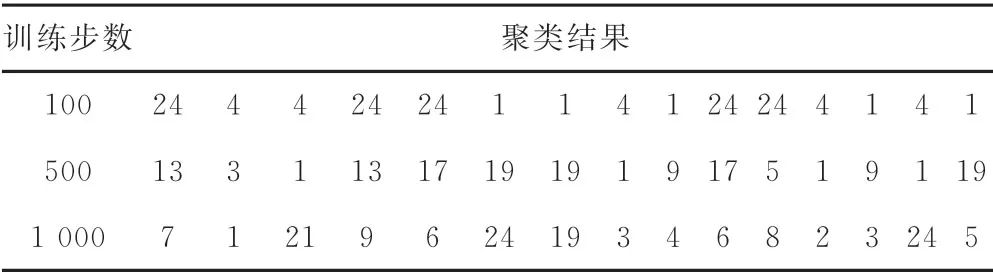
表5 网络聚类结果
SOM-RBF网络可以对工程造价成本数据进行特征抽取,经过设计和调试的网络是可以根据CSIs以及各个CSIs在总造价总所占的百分比,对数据规律进行特征提取。
3.3 WLCS的SOM-RBF网络投资估价
确定特征向量,对工程进行定量化描述,即网络输入。用Ij=(I1,I2,…,I8)表示,其中k表示第k个工程特征,Ij表示第j个工程特征的定量化数值。确定样本工程的CSIs和fcsf,即网络输出。借助MATLAB软件,SOM-RBF网络模型的输入单元为8个,即为8个同类工程特征向量,输出为CSIs每米造价用O1表示,fcsf用O2表示。
对预测值进行分析见表6。网络预测的结果和实际值之间的平均相对误差(±4%)符合投资估算精度要求(±5%)。

表6 网络预测结果分析
5 结束语
研究结果表明SOM 在对于工程特征聚类方面显示出明显的优势,是聚类分析技术在工程领域的探索应用,可以作为一种识别类似工程的方法。神经网络聚类大大减少了由于人为因素造成样本分类的误差。SOM 与RBF网络结合后,隐层节点通过SOM 聚类得到,更符合数据本身的规律,投资估算达到很好的预测效果。但是网络也存在一定缺点,参数的选取会影响网络收敛性,实验中对参数进行了反复试算,形成的误差是模型共同作用的结果,WLCS和SOM-RBF 神经网络模型结合后,最终计算结果的相对误差小于±4%,说明模型整体性能达到标准。

