箱梁底板孔洞处拉压波散射作用下动应力集中的解析解
杨旭姣,马迎瑞,王显利
(北华大学土木与交通学院,吉林 吉林 132013)
混凝土箱梁应用广泛,由于施工工艺或维修加固的需要,会在箱梁底板上人为开设大量孔洞.当地震发生时,因受持续波动力影响,箱梁底板孔洞处会产生动应力集中现象,进而影响箱梁结构的整体安全.对于箱梁孔洞问题,国内外学者已有研究:冯志新[1]研究了任意型孔静应力集中问题,并给出复变函数法的解析方法;何志刚等[2]基于变分原理研究了箱梁开裂前后的剪力滞效应,结果表明,配筋率的最大影响位置在初始开裂截面,且在均布荷载作用下开裂区段越长影响越大;朱静秋[3]用有限元分析了箱梁底板开孔对底板受力性能的影响;常立峰[4]运用反应谱分析法研究了在强震作用下箱梁桥的横、纵向受力情况,分析了箱梁桥的破坏机制,并给出了数值模拟结果;WU Y D[5]运用非线性时程分析法,通过建立概率地震需求模型,利用一阶定界法对桥梁体系的脆性进行了评价,得出了在地震作用下,桥梁体系比任何构件都更加脆弱的结论;胡超[6]、LEI Z等[7]提出了厚板拉压振动基础理论方程并给出了解析解,分析了不同参数对动应力集中的影响;HUANG H[8]提出了一种建筑模型更新方法,量化相关参数,优化遗传算法,使得桥梁评估更加准确.以上学者研究了箱梁开裂时不同的受力情况以及破坏机制,但均未考虑箱梁遭受持续波动力时,孔洞造成的拉压波散射对动应力集中的影响.本文基于拉压振动方程,以含孔箱梁底板为研究对象,在复变函数法和保角映射法的基础上,配以局部坐标系法,研究拉压波散射作用下的孔域动应力集中问题.本文的研究结果可为连续箱型梁桥设计和维修加固提供理论依据.
1 拉压波动方程及其解析
为更好地分析拉压波散射对动应力集中的影响,需要先建立拉压波动基本方程,随后进行数值模拟,得出动应力集中问题的解析解.取含孔箱梁底板为研究单元,以拉压振动方程[6]为基础,控制方程为
(1)

为了更好地研究板结构拉压振动的频散关系,保留各元素的一般性,研究该问题的谐和振动解.设广义位移函数分别为
(2)
式中:ω为拉压振动的圆频率;i为虚数单位;t为时间因子.
将式(2)代入式(1)并省略广义位移函数的符号~和时间因子t,可以得到
(3)
式中:αj(j=1,2)是弹性波波数,满足方程

(4)

(5)
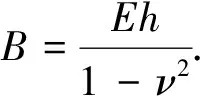
应用保角映射法,将ζ平面上孔洞边界L的外域映射成η平面上边界S的单位圆外域.整理后可表达为
ζ=Ω(η)=cη+Φ(η)
,
(6)
式中:Φ(η)为全纯函数.
将式(6)写成在极坐标系(r,β)内的方程形式,整理后可表达为
Nr+Nβ=Nx+Ny,
Nβ-Nr+2iNrβ=(Ny-Nx+2iNxy)exp(2iβ) ,
MQr-iMQβ=(MQx-iMQy)exp(iβ).
(7)
于是,在η=ρexp(iθ)平面上式(7)可写成
(8)
根据式(8),可以导出η平面上平板中广义内力的表达式为
(9)
2 拉压波散射总波场
假设在箱梁底板中有一拉压弹性波沿x轴正向入射,其表达式为
E(i)=E0eiα1xF(i)=δ1E(i)f(i)=0
,
(10)
式中:E0是入射波沿x轴方向广义位移的幅值.
拉压弹性波的总波场表达式是由入射场和散射场叠加后得出的,对于箱梁底板含多个任意形孔的情况,总波场方程可表达为
(11)
式中:j代表第j个开孔.
3 边界条件与模式系数
设箱梁底板拉压振动时孔洞在η平面上是自由边界,平板理论[6]可以满足以下6个边界条件:
(12)
式中:m=1,2;a是孔的半径.
(13)
在方程(13)的两端都乘以e-isθ,可得无穷代数方程组
(14)
其中,边界处入射波的表达式为
(15)
第j个孔洞边界处散射波的表达式为
(16)
动应力集中系数表达式
(17)

与以往只考虑0到t短时间内冲击荷载和有限元方法的数值模拟不同,本文是在明确提出动弹性状态下得出的完备解.
4 数值算例
取n=10,泊松比ν=0.3,孔径与板厚比a/h=0.1~5.0,无量纲波数α1a=0.1~5.0.动应力集中系数沿孔边的分布情况见图1~6,图中上半部分是t=0时动应力集中系数沿孔边的数值分布,下半部是t=T/4时动应力集中系数沿孔边的数值分布.图7是动应力集中系数受入射波波数影响的变化曲线.
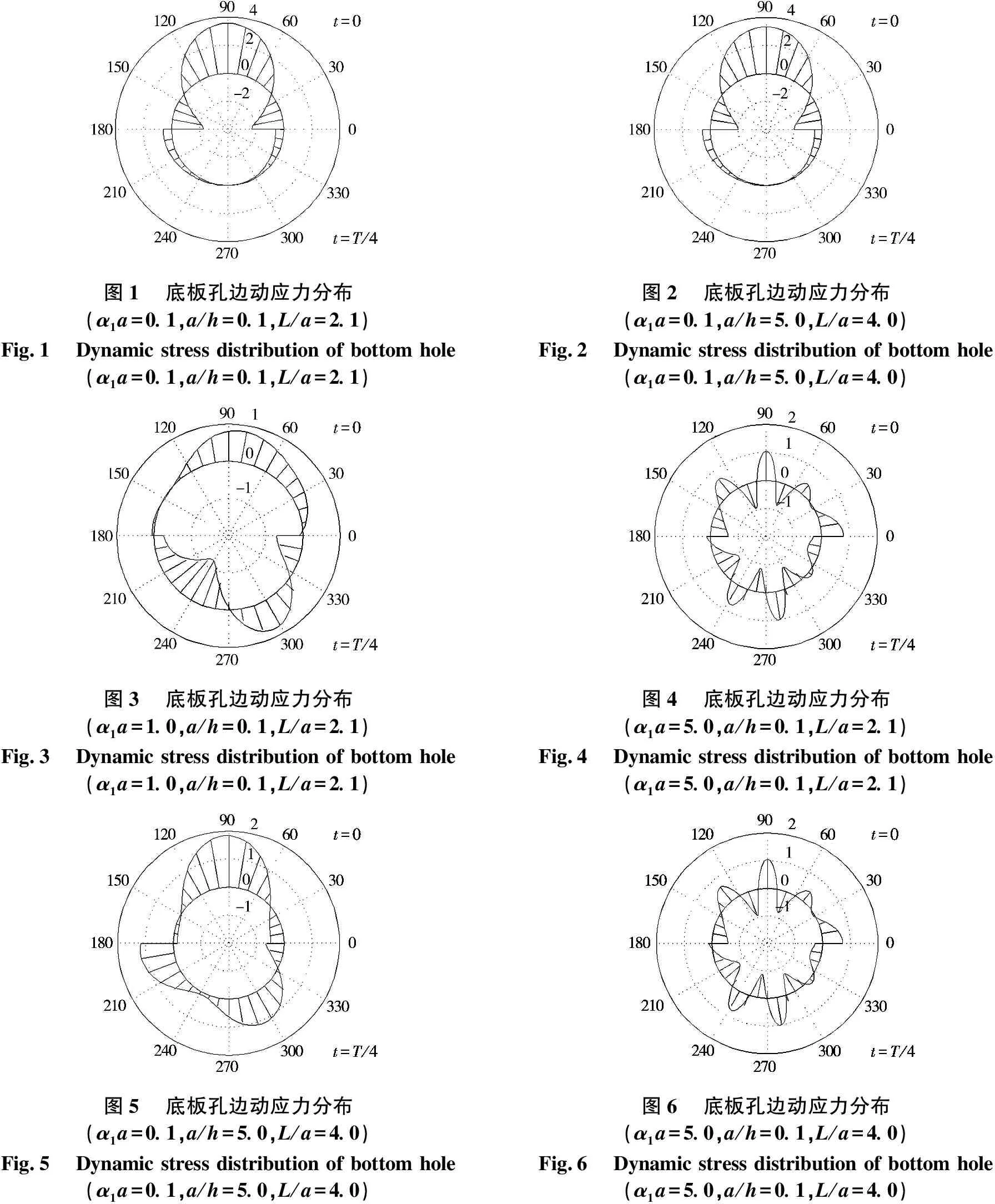
图1底板孔边动应力分布(α1a=0.1,a/h=0.1,L/a=2.1)Fig.1Dynamic stress distribution of bottom hole(α1a=0.1,a/h=0.1,L/a=2.1)图2底板孔边动应力分布(α1a=0.1,a/h=5.0,L/a=4.0)Fig.2Dynamic stress distribution of bottom hole(α1a=0.1,a/h=5.0,L/a=4.0)图3底板孔边动应力分布(α1a=1.0,a/h=0.1,L/a=2.1)Fig.3Dynamic stress distribution of bottom hole(α1a=1.0,a/h=0.1,L/a=2.1)图4底板孔边动应力分布(α1a=5.0,a/h=0.1,L/a=2.1)Fig.4Dynamic stress distribution of bottom hole(α1a=5.0,a/h=0.1,L/a=2.1)图5底板孔边动应力分布(α1a=0.1,a/h=5.0,L/a=4.0)Fig.5Dynamic stress distribution of bottom hole(α1a=0.1,a/h=5.0,L/a=4.0)图6底板孔边动应力分布(α1a=5.0,a/h=0.1,L/a=4.0)Fig.6Dynamic stress distribution of bottom hole(α1a=5.0,a/h=0.1,L/a=4.0)
对比图1和图2可以明显看出:当α1a=0.1时,动应力集中系数较为稳定,在θ=π/2方向上出现最大值,且数值分布关于θ=π/2大致对称.对比图1和图3可知:当a/h=0.1,L/a=2.1时,α1a增大,动应力集中系数分布逐渐变化,最大值仍在θ=π/2方向上,但在θ=-2π/3方向上出现了负应力.对比图2和图5可知:当a/h=5.0,L/a=4.0时,α1a值增大,动应力集中系数分布逐渐变化,最大值仍在θ=π/2方向上,但在θ=-2π/3和θ=π方向上都出现了负应力.对比图3和图4可知:a/h、L/a不变,α1a依旧增大,动应力集中系数分布呈现不规则变化,多方向出现负应力,对构件稳定性影响极大.对比图4和图6可知:α1a值较大,a/h却较小,动应力集中系数变化波动依旧强烈.
由图7可见:在入射波波数和孔径与板厚比较小时,动应力集中系数最大值为3.3.当入射波波数和孔径与板厚之比逐渐增大时,动应力集中系数波动也随之加剧,最终趋近于1.
5 结 论
本文基于拉压振动精确化方程,采用复变函数法、保角映射法和局部坐标系法,导出了箱梁底板的拉压波动方程,给出了孔洞处动应力集中系数的解析解.结合算例分析了入射波波数、孔径与板厚之比和孔间距对动应力集中系数的影响情况,得出以下结论:随着入射波波数的不断增大,动应力集中系数呈现无规则分布.当入射波波数逐渐增大到某一定值时,动应力集中系数经过波动后最终趋近于单位1;孔径与板厚比过大或过小对动应力集中系数都有影响,加剧了数值波动,出现负应力;孔洞间距的变化使得动应力分布发生复杂变化,当孔间距与孔径比小于2.1时动应力集中系数变化更加剧烈.
本次研究结果可为箱型梁桥设计施工、维修加固决策提供理论依据,在应力集中区域采取补强措施可维持地震作用下的结构安全.因箱型梁桥的受力影响因素种类繁多,在后续研究中将会继续考虑其他因素进行综合分析.

