弹性尾缘对超空泡航行体空泡形态与压力脉动特性影响的水洞试验研究

侯东伯,王聪,夏维学,李宜果,赵静

(1.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001；2.中国运载火箭技术研究院 研究发展中心,北京 100076)

0 引言

超空泡航行体在水下高速运动过程中，由于弹体全部或部分被包裹在空泡内，在减小阻力的同时也失去了部分可控水动力的作用，使得航行体受到强非线性流体动力的作用，大大增加了超空泡航行体运动控制的难度，因此水下航行体空泡的生成、发展与控制成为超空泡航行体研究的关键问题之一[1-2]。空泡形态的改变影响着航行体的沾湿区域，进而改变其动力特性。对于空泡形态特性问题，Savchenko[3]和Savchenko等[4]根据空泡形态与空泡闭合位置提出了高速运动航行体在空泡包裹下的4种运动模式；Ota等[5-6]利用空化水洞进行试验，针对不同攻角、不同空化数和雷诺数情形研究了空泡流特性，并测量了模型表面的压力；贾力平等[7]通过试验方法研究了空化器参数对形成超空泡临界空化数和通气系数门限值的影响；方城林等[8]通过数值模拟方法分析了射弹头型对空泡形态演化过程、射弹流体动力及弹道特性的影响规律；路丽睿等[9]通过开展不同头型射弹低速倾斜入水试验，研究了射弹头型对入水空泡、运动速度、俯仰角和阻力系数的影响规律；邓飞等[10]提出了一种应用于水下射弹的双圆盘空化器，并在高速循环水洞中对其空泡生成特性和形态特性进行了实验研究；王威等[11]通过数值模拟研究了阵风流作用下通气超空泡形态的变化特性。

有效控制空泡形态对于预估航行体的动力特性具有重要意义。白涛等[12]采用水洞实验方法获得了超空泡航行体模型在空化器角度变化时的超空泡形态和超空泡内外压力数据；Wang等[13]设计了水洞试验，对带有不同角度空化器的模型进行了测试，设计了超空泡航行体的控制规律并给出了仿真验证；周后村等[14]基于有限体积法，研究了超空泡航行体在不同空泡流型及不同控制面舵角情况下控制面与主空泡之间的相互作用；裴譞等[15]通过缩比模型试验对通气超空泡的生成和尾翼舵角的力学特性进行了研究，获得了尾翼舵角对升力的影响规律及尾翼舵效随攻角和通气量变化的规律。目前对超空泡航行体的控制主要通过空化器攻角以及航行体尾部控制面舵角的改变来实现，缺少航行体尾部弹性尾缘对超空泡航行体控制的研究。

为了研究空泡闭合位置的变化从而增加水下航行体运动控制效果，本文设计了带有可变刚度弹性尾缘的超空泡航行体模型，获得了航行体模型不同变形状态与不同通气量对空泡形态及航行体表面压力变化的影响特性，为水下超空泡航行体的运动控制研究提供了技术参照和数据支撑。

1 通气试验装置与模型

1.1 通气试验装置

试验在哈尔滨工业大学HT-01型循环式通气水洞中完成，该试验系统主要由水洞及其操控系统组成，图1所示为水洞整体示意图，其中工作段为0.26 m×0.26 m×1.00 m的长方体。为便于观察，工作段四周均用透明有机玻璃装配，下游尾水罐用来分离通入的气体，以保证通气试验连续进行。

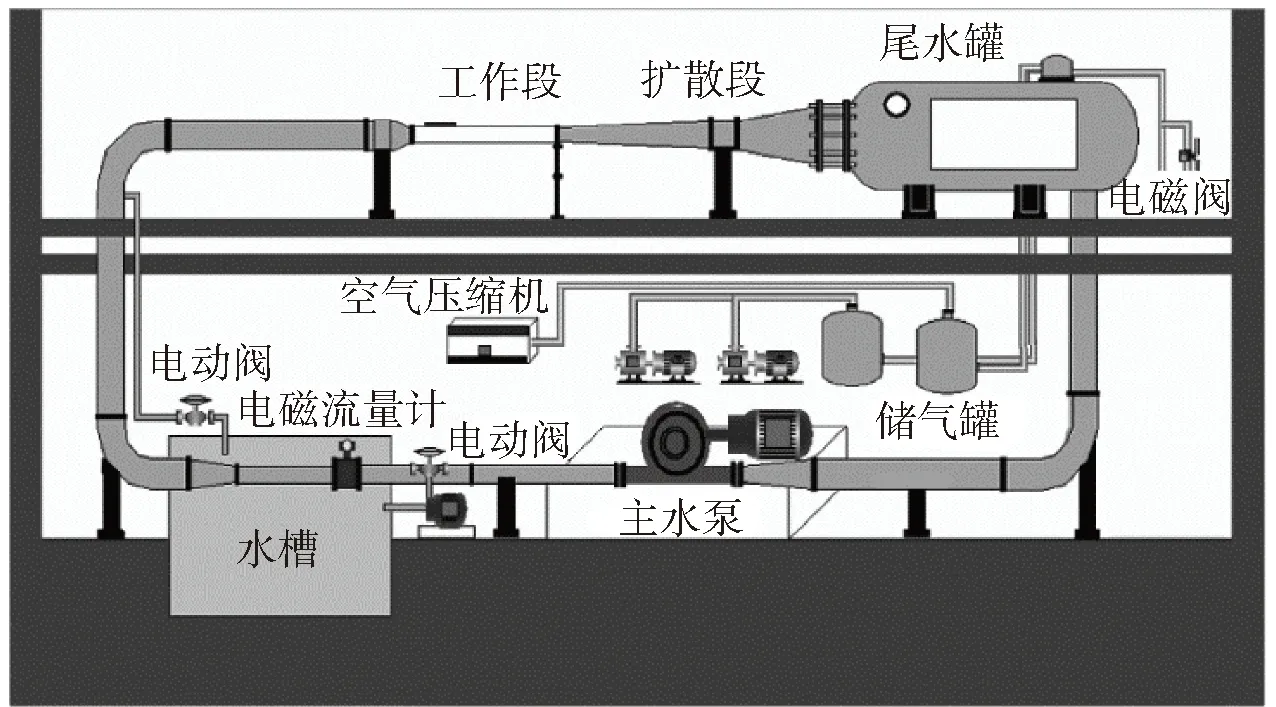
图1 超空泡循环水洞示意图Fig.1 Schematic diagram of water tunnel

试验的整体方案示意图如图2所示，其中数据采集系统线缆由支撑杆内部引出，以防干扰流场结构。试验中采用德国瑷荔德公司生产的METRON Prosilica GE680C型工业相机进行图像数据采集，设置拍摄帧率为200 帧/s，曝光时间为3/10 000 s.由于拍摄曝光时间较短，为保证照片的清晰度，试验中使用两盏功率1 000 W新闻灯构成的背光源和一盏功率1 000 W新闻灯构成的前光源，在背光源前架设柔光屏，令入射光线漫射，以达到流域亮度均匀一致的效果。

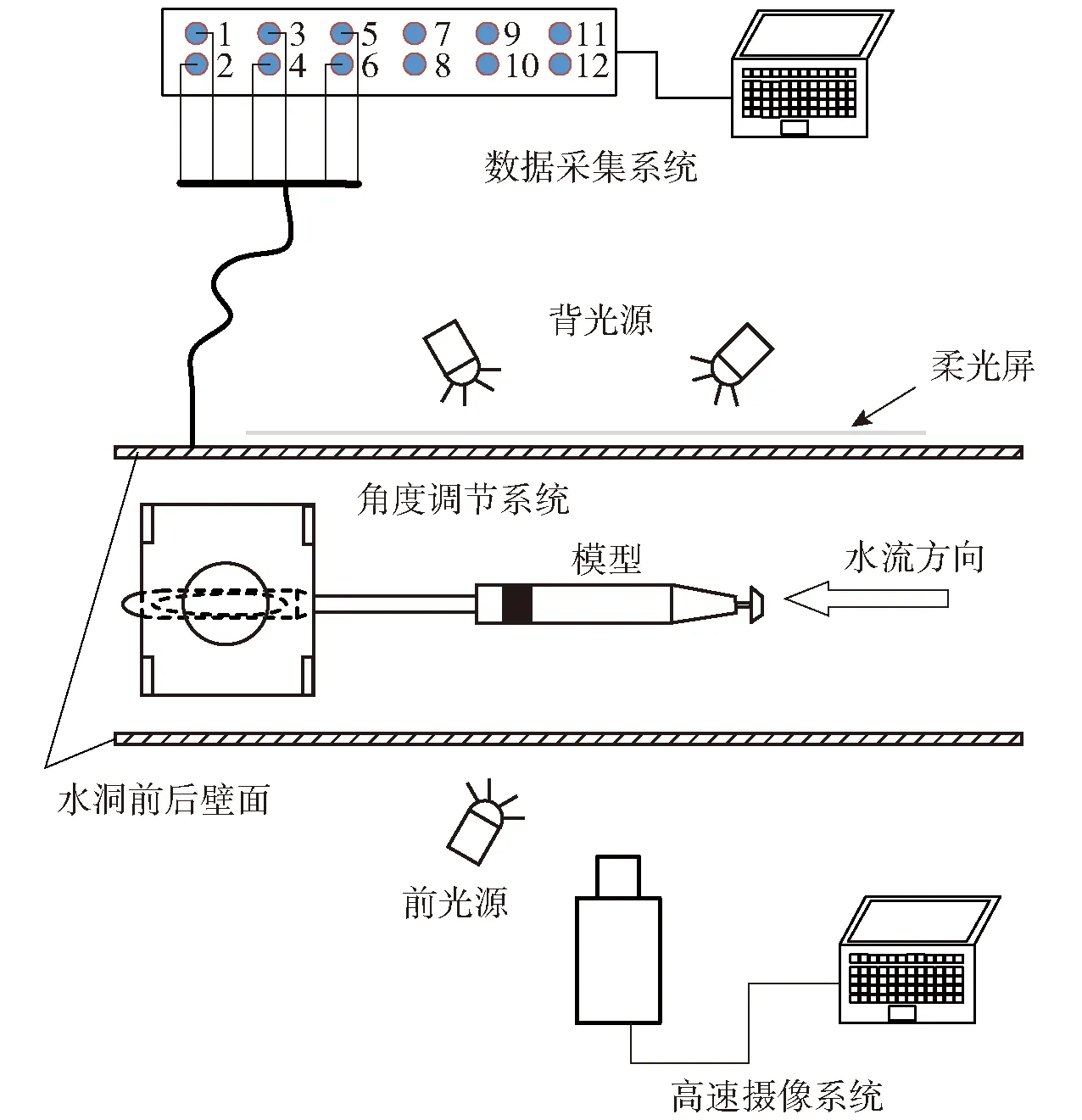
图2 试验方案示意图Fig.2 Schematic diagram of experimental setup

压力脉动信息由江苏东华测试技术股份有限公司生产的动态测试系统采集，采样频率为2 kHz.水洞工作段流速可由安装在水洞管路上的电磁流量计换算获得，在0～18 m/s范围内连续可调。试验时，当流场流速与空泡形态均达到稳定状态后，同时进行图像数据与压力脉动信号的采集。

1.2 试验模型

图3(a)所示为超空泡航行体模型实物图：试验模型主体采用铝合金材质；弹性尾缘材料为丁基橡胶，在内侧气腔与外侧流场压力差作用下产生形态与刚度的变化；弹性尾缘前后载体均采用不锈钢材质增加强度。图3(b)所示为航行体模型原理图：模型整体长度575 mm，最大直径40 mm；1号空气压缩机与稳压罐连接，为弹性尾缘内侧气腔提供稳定压力，可使尾缘产生变形并发生刚度的改变；2号空气压缩机由通气管连接至空化器处，为模型提供稳定流量通气以产生超空泡；两条通气管路分别采用独立的气源与管路，互相不存在影响；压力传感器P4安装在水洞工作段前端壁面上。图3(c)所示为弹性尾缘部位的设计图：由前中后3部分组合而成，中部不锈钢载体与丁基橡胶之间形成气腔；橡胶前后两端在凹槽处由连接处压紧，并放置密封圈以保证气室的气密性；压力传感器P1、P2、P3分别安装在弹性尾缘的前中后3处位置，与模型后基准面的距离分别是16 mm、50 mm、81 mm.

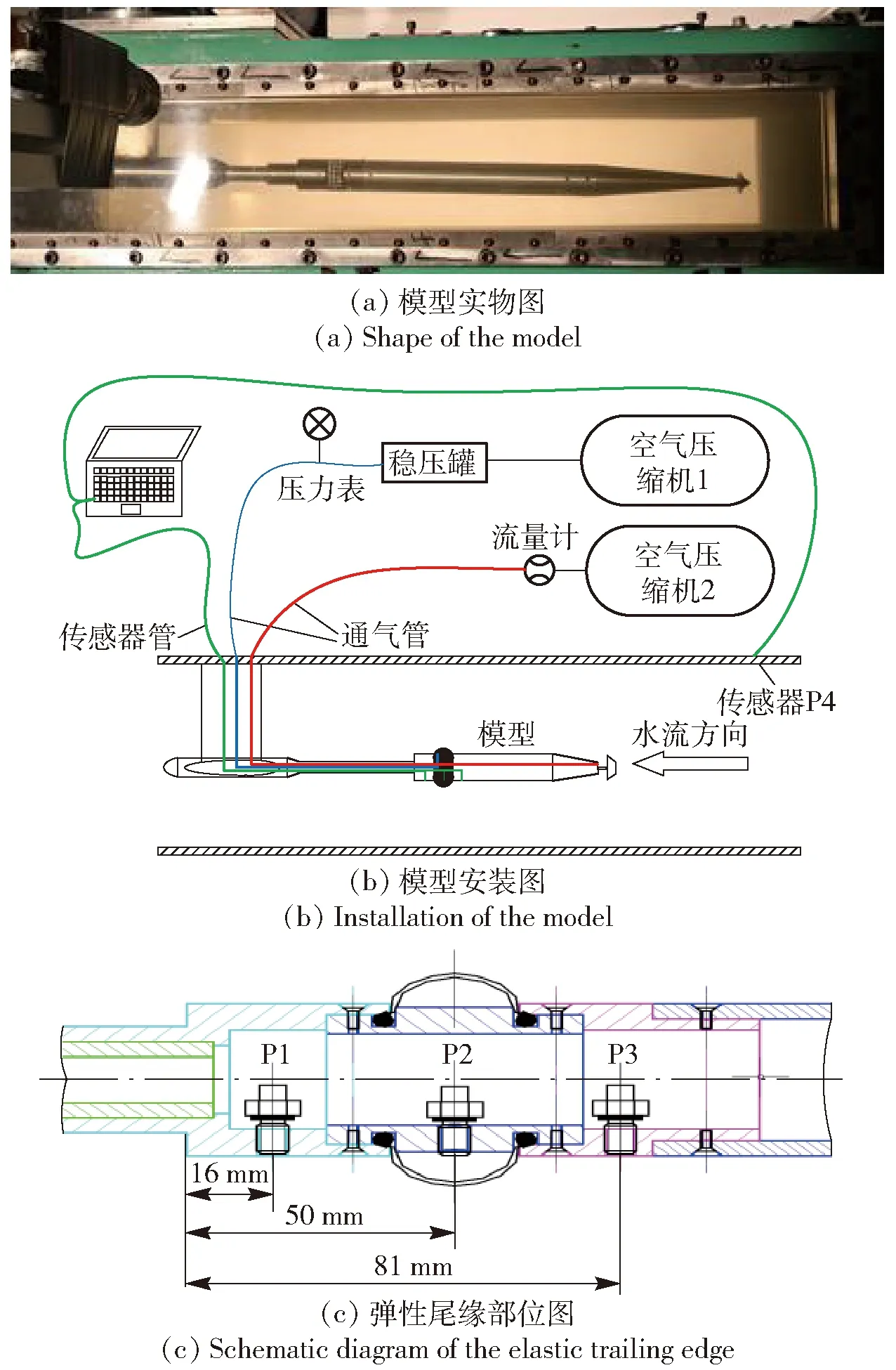
图3 试验模型示意图Fig.3 Schematic diagram of experimental model

对试验模型在弹性尾缘不同状态下的航行阻力进行预估，结果如表1所示。由表1可以看到，弹性尾缘发生形变后，超空泡航行体减阻效率有所下降，因此尾缘形变状态适用于对航行体有较高机动要求的情况，而在直航状态下尾缘应保持无形变状态。

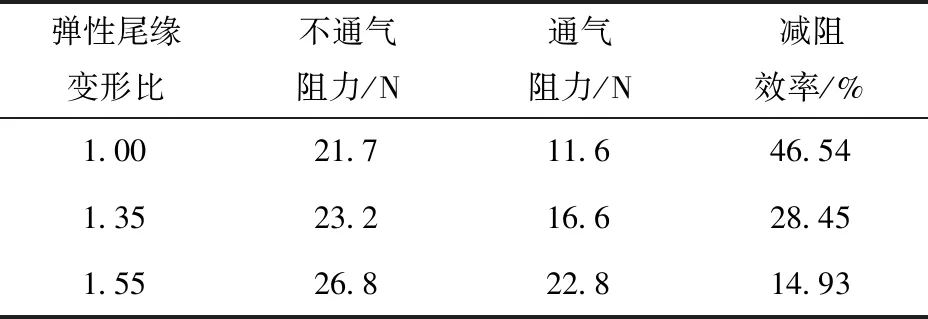
表1 通气超空泡航行体阻力变化表Tab.1 Resistance change of ventilated supercavitating vehicle

2 试验结果分析

由于试验模型长细比较大，在重力作用下，空泡尾部上漂明显。当弹性尾缘无变形且通气量足够时，航行体上表面形成贯通超空泡，下表面处的空泡只能闭合在弹性尾缘前方，为使空泡覆盖模型下表面传感器位置以进行对比研究，本文中将试验模型顺时针旋转2°.本文试验过程均处在流速8 m/s，水洞工作段压力90 kPa的环境下。

2.1 可变刚度弹性尾缘变形特性

无空泡时对弹性尾缘形态的观察效果更加明显，图4给出了在一定来流速度下不同压力差的弹性尾缘变形情况。图4中：压差系数Cp分别为0、0.18、0.24；随着压差系数的逐渐提高，弹性尾缘变形比ε分别为1.00、1.35、1.55.

图4 弹性尾缘变形图Fig.4 Deformation of elastic trailing edge

对尾缘压力差与变形量做无量纲处理，压差系数Cp与变形比ε分别定义如(1)式和(2)式：

Cp=Δp/p∞，

(1)

式中：p∞为水洞工作段环境压力，通过安装在水洞工作段区域侧壁的压力传感器P4测得；Δp=p-p∞为尾缘内压力与环境压力的差，其中尾缘内压力p由传感器P2测得。

ε=d/D，

(2)

式中：D为模型主体直径；d为尾缘直径。由于尾缘直径在水流环境下存在变形，其直径d通过高速摄像拍摄的图像获得，即为像素直径。为了保证模型直径也为像素直径，模型直径D也通过图像测量得到。

由图4可见，在图4(a)中压差系数为0，弹性尾缘由于自身弹性而紧缚于模型上。随着压差系数的增大，弹性尾缘发生弹性变形以产生恢复力，在与压差力达到平衡后变形结束。对比相同来流速度下3组不同压差系数的弹性尾缘变形情况，可知弹性尾缘变形随着压差系数的增加而不断增大。同时，由于尾缘内气压的增大，尾缘的刚度随着其变形的增大而增大。

2.2 弹性尾缘区域空泡形态特性

在不同压差与不同通气率下，对带有可变刚度弹性尾缘的超空泡航行体模型进行水洞试验，通过对比分析可以得出弹性尾缘区域空泡形态特性。

定义空化数如下：

(3)

式中：pc为空泡内压力，通过传感器P3测得；v∞为来流速度；ρ为液体密度。

对通气量做无量纲处理，通气率定义如下：

(4)

式中：Q为与空化器连接气路的通气量，可以由流量计直接读出；S为空化器最大横截面面积。

如图5(a)、图5(b)所示，此时弹性尾缘无变形，通气率达到0.08后空泡迅速发展，覆盖至航行体下表面尾部，而上表面空泡闭合在尾缘前方。通气率变为0.42后，发现随着通气量的继续增大，航行体上表面空泡的闭合点不断向后延伸，最终将弹性尾缘包裹进空泡内。此阶段弹性尾缘与空泡之间不发生耦合作用。

图5 通气超空泡航行体形态图Fig.5 Patterns of ventilated supercavitating vehicle

如图6(a)所示，通气率处于0.08～0.12范围时，弹性尾缘变形比与刚度随压差的增加而增大，无变形状态下空泡闭合在航行体上表面弹性尾缘前方，而航行体下表面被贯通形成超空泡。从图6(b)、图6(c)中可以看出，随着弹性尾缘的变形，空泡在航行体下表面的闭合点位置前移至尾缘前方，同时在尾缘后方产生愈加剧烈的尾空泡。这是因为弹性尾缘变形后，水流冲击尾缘前端，造成局部高压，空化数升高导致空泡迅速闭合在尾缘前方，而弹性尾缘后方由于脱体绕流作用压力减小，空化数降低导致生成尾空泡。

图6 不同刚度尾缘空泡形态图(α为0.08～0.12)Fig.6 Patterns of cavitation of different trailing edges(α=0.08-0.12)

通过观察图7中通气率处于0.37～0.44范围时弹性尾缘的流场控制特性，发现空泡形态的变化规律与通气率处于0.08～0.12范围时相同，仅由于通气量的增大导致弹性尾缘后方的尾空泡更加明显，表明此可变刚度弹性尾缘在通气率为0.08～0.44范围内时，对空泡闭合点位置具有有效的影响。

图7 不同刚度尾缘空泡形态图(α为0.37～0.44)Fig.7 Patterns of cavitation of different trailing edges(α=0.37-0.44)

2.3 弹性尾缘区域压力脉动特性

图8 不同刚度尾缘压力信号(α=0)Fig.8 Pressure signals at different trailing edges(α=0)

为研究弹性尾缘不同刚度对其附近压力的影响，将压力数据进行处理分析。通气率为0时各采集点压力数据如图8所示，参考图4(a)、图4(b)、图4(c)可知此时航行体表面无空泡，流场处于稳定状态。图8(a)中尾缘无变形并紧缚于航行体上，因此传感器P2处数据为尾缘向内挤压的压力示数，无参考意义。对比图8(a)、图8(b)、图8(c)可以发现，随着弹性尾缘刚度的增加，水洞工作段流场压力不变，而航行体表面压力变大且传感器P1压力波动幅值明显增大。这是因为弹性尾缘刚度变化后，在来流作用下传感器P3处位于迎流高压区，导致其压力变大；而传感器P1处受到绕流尾涡在生成与脱落过程中的冲击作用，因此该位置压力变大且波动幅值增大。

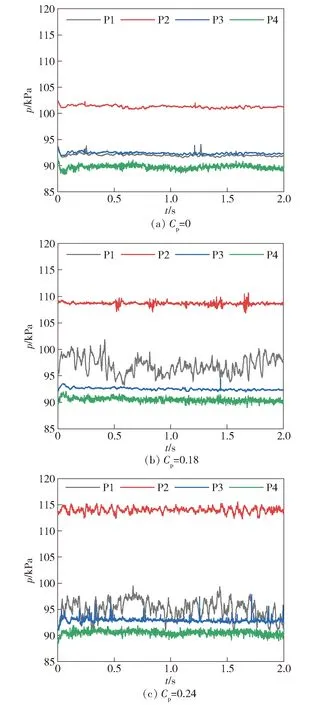
图9 不同刚度尾缘压力信号(α为0.37～0.44)Fig.9 Pressure signals at different trailing edges(α=0.37-0.44)

对通气率0.37～0.44范围内的压力信号进行分析，如图9(a)所示，压差为0时弹性尾缘处于无变形状态，此时尾缘前后压力基本相等，结合图7(a)可知航行体下表面被包裹在空泡内，失去了水动力作用因此压力较小。观察图9(b)中压力变化可知，此时弹性尾缘变形比为1.35，传感器P3处压力保持不变而传感器P1处压力变大且压力波动幅值增大，结合图7(b)可知此时航行器下表面的空泡闭合点前移，但仍然跨过传感器P3处闭合在尾缘前，传感器P3处仍位于空泡内，压力基本不变，而传感器P1处变为沾湿状态导致压力增大，且由于尾涡的干扰产生波动。再观察图9(c)中的压力信号发现，此时尾缘变形比为1.55，传感器P3处压力仍保持不变而传感器P1处压力略微降低；结合图7(c)，发现尾缘后方产生尾空泡，导致传感器P1处沾湿面积减小从而压力下降，而位于航行体下表面的空泡闭合点在尾缘与传感器P3之间波动，导致传感器P3处压力产生振幅突变。

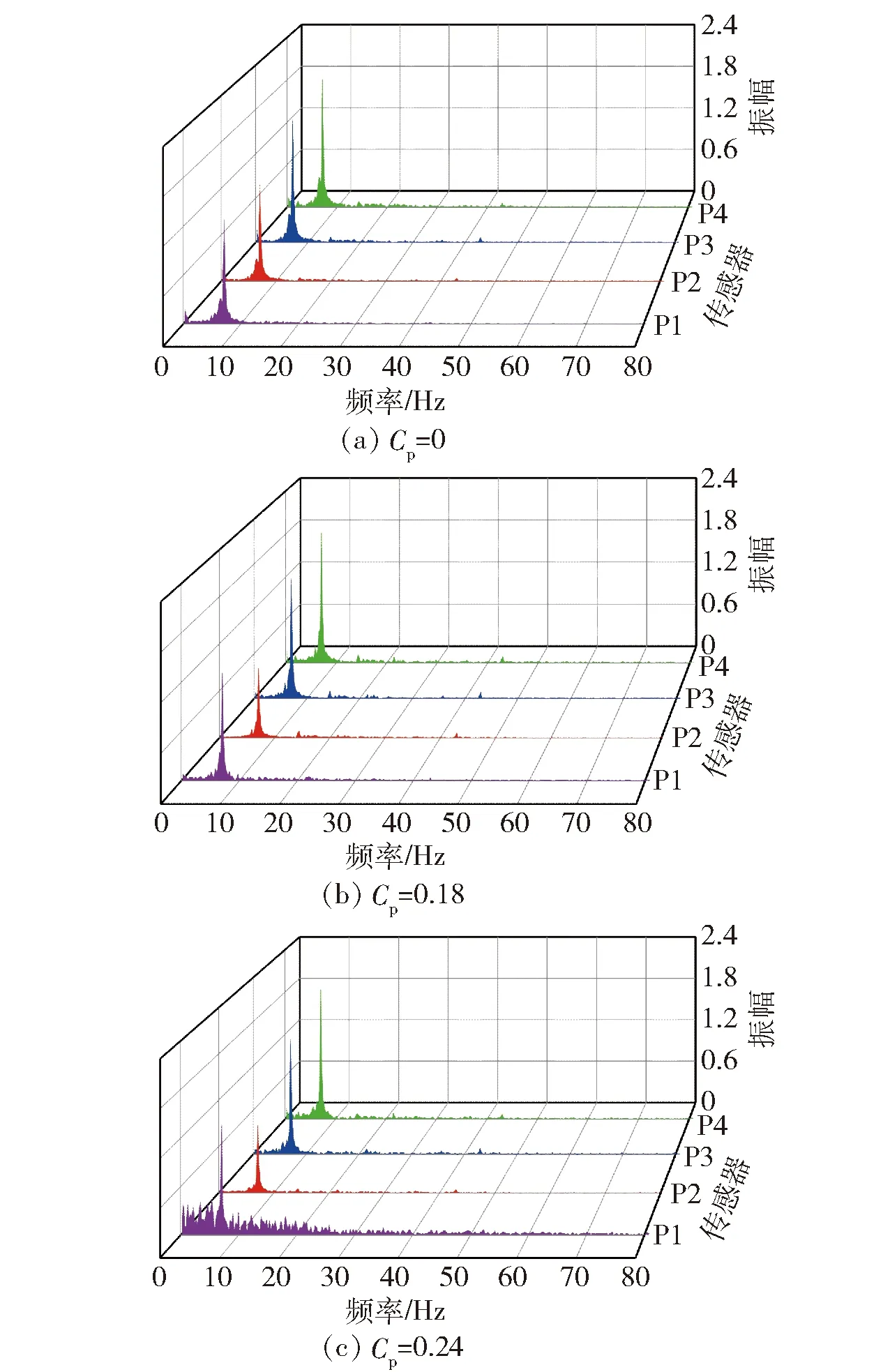
图10 不同刚度尾缘压力信号频谱分析(α=0)Fig.10 Frequency spectra of pressure signals at different trailing edges(α=0)

为了更好地分析弹性尾缘区域压力的周期振荡特性，选取通气率为0和0.37～0.44范围内测得的压力时间信号进行快速傅里叶变换(FFT)分析。从图10中可以得到，通气率为0时不同传感器压力信号在尾缘不同刚度条件下均存在7.08 Hz的主脉动频率，通过传感器P4处压力信号可以判断出此频率为水流冲击产生的固有频率。通气率为0时传感器P2、传感器P3与传感器P4处压力信号不随弹性舵变形而变化，频率集中在0～10 Hz；传感器P1处压力信号在变形比为1.55时具有更宽的频率分布，分布范围为0～30 Hz，这是因为尾缘后方产生了不稳定绕流尾涡，尾涡的波动造成传感器P1处压力的振荡。

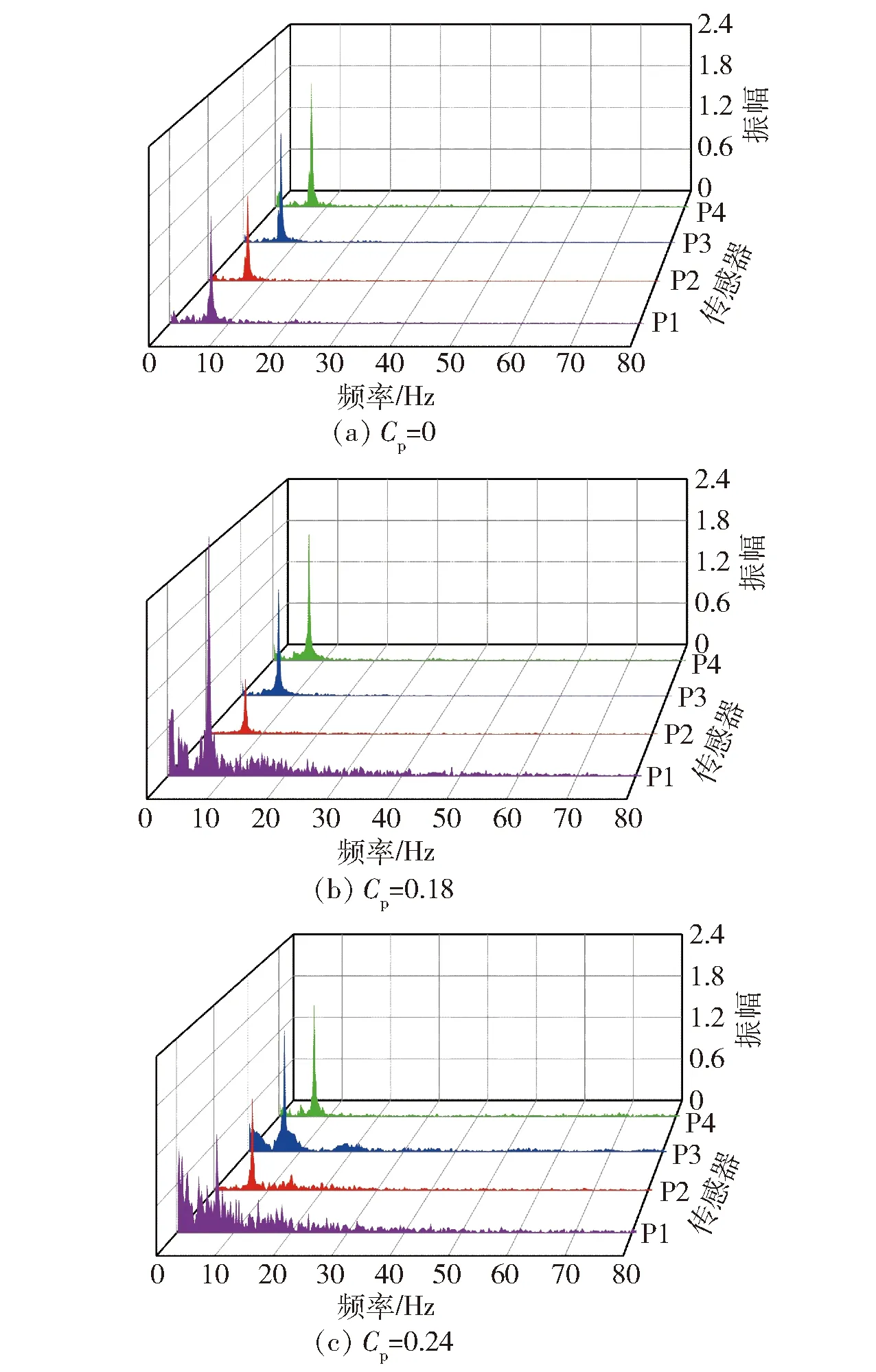
图11 不同刚度尾缘压力信号频谱分析(α为0.37～0.44)Fig.11 Frequency spectra of pressure signals at different trailing edges(α=0.37-0.44)

通气率在0.37～0.44范围内的压力频谱分析如图11所示。由图11可见，在不考虑水流冲击频率的前提下，变形比为0时航行体被包裹在空泡内，压力振荡基本消失。变形比为1.35时传感器P1处位于主空泡外部，其压力频率集中在0～40 Hz范围内，频率峰值为0.73 Hz，这是因为尾缘后方尾空泡的波动造成的。变形比为1.55时传感器P1处受更加剧烈的尾空泡波动影响，压力振荡更大，频率峰值为0.49 Hz；传感器P2与传感器P3受到主空泡闭合点波动影响，传感器P2处产生峰值为14.41 Hz的主频率，而传感器P3处产生了峰值为0.24 Hz的主频率，传感器P2处压力频率远大于传感器P3处，表明空泡闭合点更倾向于向尾缘位置波动，也验证了尾缘影响空泡闭合点位置的有效性。

3 结论

本文针对水下超空泡航行体尾部空泡形态特性及压力脉动特性，利用通气超空泡水洞进行了带有可变刚度弹性尾缘的水下超空泡航行体模型试验研究。得到以下主要结论：

1)研制了带有可变刚度弹性尾缘的水下超空泡航行体模型，测试得到了不同压差系数及通气率下的通气空泡高速图像及特征点压力数据。

2)获得了可变刚度弹性尾缘形态随压差变化特性，尾缘变形随其两侧压力差的增加而增大，同时尾缘刚度也随之提高。

3)获得了弹性尾缘在不同变形状态下与空泡形态变化的关系，尾缘无变形时对空泡形态无影响，发生变形后空泡闭合点前移至弹性尾缘前方，无法跨过尾缘形成贯通超空泡，表明尾缘有效影响了空泡闭合点位置。

4)获得了弹性尾缘在不同变形状态下与特征点压力变化的关系，尾缘发生变形后其后方进入沾湿状态，导致表面压力增大，提高了航行体模型水动力作用效果。