基于模糊PID算法吸附机器人转向控制系统
申 鹏 胡东鑫
(1.哈尔滨商业大学 计算机与信息工程学院 哈尔滨150028;2.哈尔滨商业大学 轻工学院 哈尔滨150028)
随着时代的发展,吸附式墙壁机器人的研究逐渐深入,并大量的投入清洁市场中,但传统的吸附式擦窗机器人在意外碰撞后,会导致机体倾斜地移动,从而偏离设定的N型轨迹,容易造成机器人对墙壁的重复擦拭,降低了擦拭效率[1]。为了解决这一问题,本文提出了基于模糊PID吸附式机器人转向控制系统,将模糊控制的思想与传统的PID矫正方法进行结合,机器人会对当前状态进行模糊判断,并迅速做出对应的响应,使得该系统具有自适应整定功能,该系统在机器人做大幅度转向的过程中效果较好[2]。
1 系统的数学模型
1.1 直流电动机系统分析
吸附式机器人通常采用大功率直流电动机,以保证其在墙壁上移动以及差速转向。
电动机回路电压为:
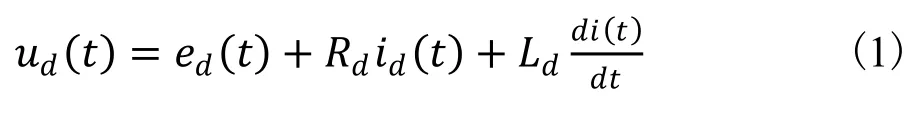
电动机电枢反电势为:

电动机电枢回路电流为:

电动机电磁时间常数为:

式中: Rd为电动机电枢回路电阻;Ld为电动机电枢回路电感;Tm为电动机机电时间常数。
联立可得电动机的动态微分方程式:

对上式进行拉氏变换可以得到电动机的传递函数为:

1.2 转向系统分析
当吸附式机器人两侧履带不相同时,可实现转弯,履带理想的转弯情况,如图1所示,由三角公式可得:


图1 机体转向分析图
实际上机器人在运动过程中,其两侧的履带会出现滑移现象,假设两侧履带i=max{il,ir},滑移率相等,且取滑移率:

代入公式(8)可得:

式中:R为转向半径, B为履带间距,履带左右两侧线速度分别为vl和vr。
Bekker理论提出的履带最大牵引力与地面因素之间关系式[3]:
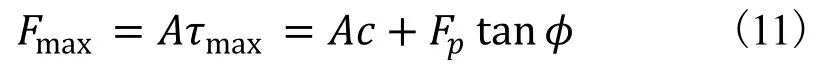
其中 Fmax为履带所受最大牵引力; A为履带与黑板的接触面积; c为墙壁黏着系数;Fp为机器所受的吸附力;φ 为内摩擦角。
同时得出履带滑移率i :

其中, K为黑板剪切变形系数;F为履带实际牵引力;机器在受的吸附力均匀作用时,其两侧履带单位长度所受压力为:

其中,L 为履带与黑板接触长度:机器转弯过程中所受的横向扭矩Mf:

其中:μx为转向摩擦系数,与接触面和转动半径有关。
通过俄国尼基金教授在实验得出经验公式可知:
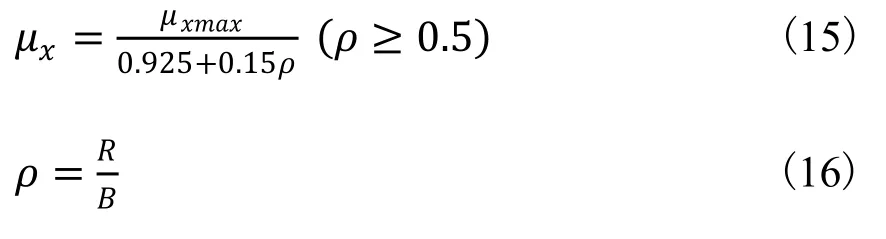
其中μxmax为在各种接触面上的最大转向摩擦系数; R为机器器转动半径;B 为两履带直接的中心距; ρ为相对转动半径,当ρ<0.5 时,μx接近于μxmax。
又有在转动过程中动力学平衡得:

其中Fl/Fr为左/右侧履带所受的实际牵引力; fl/fr为左/右侧履带所受的纵向阻力;ay为机器运动过程中纵向加速度;α为转动过程中的角加速度。
进入到稳定转动过程以后,其转动半径固定即vl/vr处于匀速状态。此时机械纵向加速度ay,转动角加速度α为0,代入公式(17)、(18)可得:
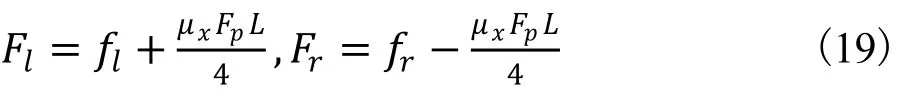
联立公式(11)、(12)、(19)得:
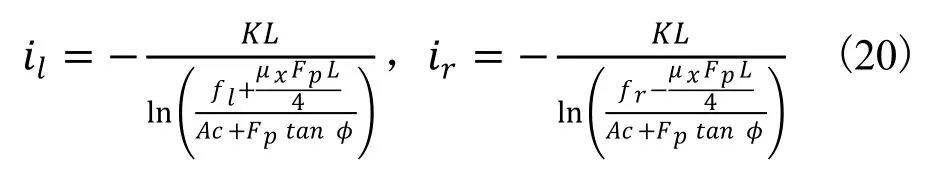
由式(11)得滑移率i 随横向摩擦系数μx改变而改变,又有μx与相对转动半径ρ有关。联立公式(20)、(15)、(16)、(19)得:

由上式可得滑移率i只与vl、vr有关。

R为转向半径,L 为履带间距,vc为中心线速度,wc为中心角速度,履带左右两侧线速度分别为vl和vr,两侧履带速度差为vh;
对上式进行拉氏变换可以得到的传递函数为:
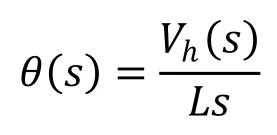
2 模糊PID控制算法
2.1 PID控制原理
PID调节器是一种线性调节器,其输入的是系统的偏差e(t) ,输出的是控制量u(t) 。系统偏差通过比例、积分和微分的线性组合从而构成控制量,对被控对象进行准确的控制。

式中Kp的作用是加快系统的响应速度,提高系统调节精度, Ki的作用是消除系统的静态误差, Kd的作用是加快系统的调节速度,减少控制系统的偏差,改善控制过程动态品质,通过这三种调节方式改善了系统的动态响应[4]。
PID控制增量式:

相比于位置式PID控制器,增量式PID控制器不需要累计误差,输出控制量为∆u(t) ,比u(t) 小很多,对系统冲击性小,可靠性更强。
2.2 模糊PID控制
模糊 PID控制器则是以误差e和误差变化ec作为输入,利用设定好的模糊控制规则表1,找出PID三个参数与e和ec之间的模糊关系,在运行中不断检测e和ec,根据模糊控制原理来对 3个参数进行在线修改,以满足不同e和ec时对控制参数的不同要求,而使被控制对象有良好的动、静态性能。

表1 模糊控制规则表
Kp, Ki, Kd的模糊控制规则表建立好后,将系统误差e 和误差变化率ec 变化范围定义为模糊集上的论域。
其模糊子集为:
e, ec= {NB,NM,NS,ZO,PS,PM,PB},子集中元素分别代表负大,负中,负小,零,正小,正中,正大,设e, ec和Kp, Ki, Kd均服从正态分布,因此可得出各模糊子集的隶属度,根据各模糊子集的隶属度赋值表和各参数模糊控制模型,应用模糊合成推理设计PID参数的模糊矩阵表,查出修正参数代入下式子计算[5]:
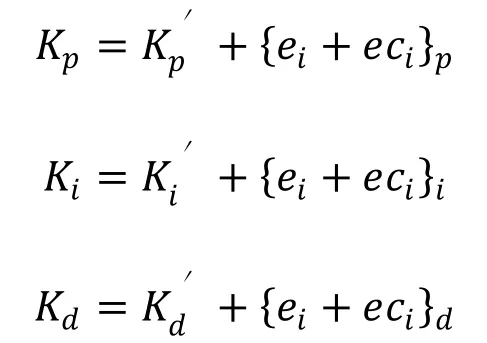
控制系统通过对模糊逻辑规则的结果处理、查表和运算,完成对PID参数的在线校正。
3 测试与分析
如图2所示,由角度传感器实时测量机体角度值,将角度误差值和角度误差值的变化率作为输入,通过设定模糊控制规则表,得到当前最佳的Kp、 Ki、Kd的控制值,输出对应的PWM值,改变履带之间的速度差,从而调节机器的姿态,使其沿着设定的路线移动[6]。

图2 转向控制系统结构图
现实中的吸附式机器人转向系统函数过于复杂,根据机器人自身的特点简化传递函数,并基于模糊PID控制的原理,对系统进行实时的调节,在simulink软件中进行在线仿真,如图3所示。相比于传统PID控制方法,采用模糊 PID 的控制方法,转向系统避免了超调,动态特性有了显著的提升。
4 结语
本文基于模糊PID算法对吸附式机器人进行转向控制,基本上达到了预期的效果,机器在移动的过程中不断矫正自身的姿态,按照原始路线进行移动。在Simulink软件进行在线仿真中,分别用PID和模糊PID矫正方法对系统进行测试,通过对相应的曲线进行对比,对目标值和相应时间进行分析,可以得出模糊PID控制方法够在满足吸附式机器人控制要求的基础上对其优化,稳态误差小,静态误差小,快速且准确,是一种优良且可靠的控制方法[7]。
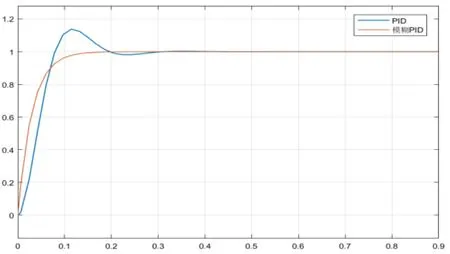
图3 仿真结果

