基于阻尼器参数选择的桥梁结构抗震分析

杨 磊，陈阳阳，孟 江

（黄河勘测规划设计研究院有限公司，河南 郑州 450000）

0 引言

斜拉桥是大跨度桥梁的主要桥型， 由于跨越能力强，常被用于跨越大江、大河。 该结构的支承体系通常采用漂浮或者半漂浮体系［1］。 该体系有利于耗散地震能量，减小桥塔在地震作用下的响应，但同时也会造成主梁的较大位移，在极端情况下，会导致主桥和引桥发生碰撞。为避免该情况的发生，通常在桥梁上设置阻尼器来协调主梁位移和桥塔内力［2-3］。桥梁常用阻尼器有钢制阻尼器和液压阻尼器2 种。 钢制阻尼器是利用钢材的塑性变形来耗散能量的。 该类阻尼器制造工艺简单，坚实耐用，具有较大的耗能能力，缺点是体积较大，需利用自身变形耗散能力，屈服后需更换处理。 液压阻尼器是利用活塞前后压力差使油流过阻尼孔产生阻尼力。 该类阻尼器体积较小，产生的阻尼力具有方向性。在桥梁纵向位移控制中，通常采用液压阻尼器。

液压阻尼器提供阻尼力的大小取决于阻尼器参数的选择。如果阻尼器提供的阻尼力较小，桥塔的内力就会较小，主梁就会产生较大的位移，可能会与引桥发生碰撞；反之，阻尼力过大，主梁产生的位移就会减小，桥塔内力会有显著增加。 因此，液压阻尼器参数的正确选择是桥梁抗震设计中关键的一环［4-5］。笔者试以某大跨度斜拉桥为背景， 通过对液压阻尼器中阻尼系数的研究来分析大跨度斜拉桥纵向的抗震性能， 探析阻尼器阻尼系数的变化对结构关键部位地震响应的影响，以期供类似工程参考。

1 液压阻尼器力学原理

1.1 液压阻尼器的构造

液压阻尼器主要由油缸、活塞杆、液压介质（油）和活塞构成，其结构如图1 所示。

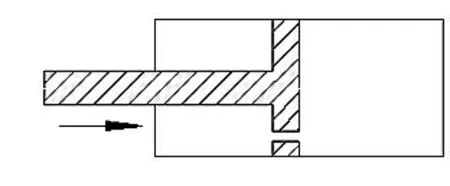
图1 液压阻尼器构造示意图Fig.1 Hydraulic damper structure schematic diagram

1.2 阻尼力的计算

液压阻尼器的阻尼力是由活塞在外力作用下推动阻尼介质， 使其流经预先设置的间隙或者孔洞而产生的。 在阻尼力产生的同时，还会发生能量转化。所以，在桥梁上设置液压阻尼器，可以将地震输入的能量转化为热能而散失， 从而达到控制结构振动的效果。液压阻尼器在外力作用下产生阻尼力。阻尼力表达式如式（1）所示。

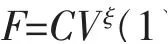
式中：F 为阻尼器提供的阻尼力；C 为阻尼系数；ξ 为阻尼指数，其取值范围为0.1～2.0。

2 建立模型

2.1 工程概况

某桥为两塔三跨桁架式斜拉桥， 桥长为1 290 m，主跨长度为630 m，边跨设置辅助墩，桥型布置如图2 所示。 该桥主梁为钢桁梁，N 型桁架，横断面采用三片主桁的形式，对应采用三索面布置。桥塔为钻石型桥塔， 塔高220 m。 主塔及桥墩处的三片主桁下，均设有纵向刚性支座，纵向为活动。 为避免主梁纵向出现过大位移而导致结构碰撞， 在主塔和主梁交界处， 安装纵向液压阻尼器。 在横向地震力作用下，主梁有可能会和主塔发生碰撞，所以在主塔和横梁上设置支座，以约束主梁的横向位移。

在该桥主塔与主梁连接处， 设置6 个液压阻尼器，全桥共设置12 个液压阻尼器。 当受到地震作用时，阻尼器产生相应的阻尼力来限制主梁的位移，同时也可以调整结构关键部位的受力特性， 如塔顶位移、主梁位移、塔底内力等。

图2 桥型布置图Fig.2 Layout of bridge type

2.2 结构有限元模拟

采用ANSYS 有限元软件建立斜拉桥的有限元模型。 桥塔采用BEAM44 单元模拟，其截面特性采用实际截面导入；斜拉索采用LINK8 单元模拟，对拉索施加初应变来考虑拉索的预应力效应， 并考虑弹性模量的折减；主桁架采用BEAM44 单元模拟；塔梁之间纵向液压阻尼器采用COMBIN14 单元模拟。 其中，COMBIN14 单元由两个节点、一个弹簧常数k 和阻尼系数CV1、CV2组成［6］。 COMBIN14 单元的几何模型如图3 所示，结构有限元模型如图4 所示，液压阻尼器与主梁的联系情况如图5 所示。

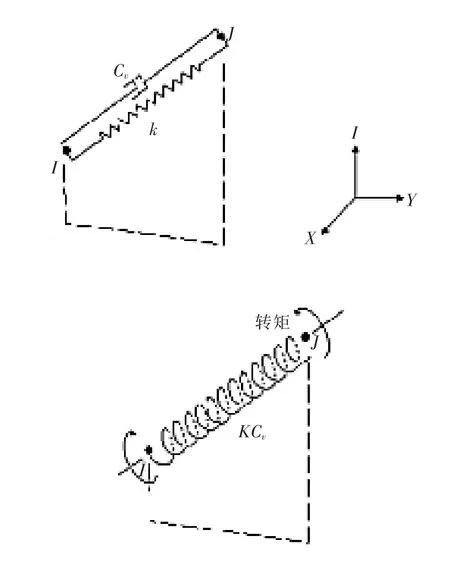
图3 COMBIN14 单元几何模型Fig.3 COMBIN14 element geometric model

图4 结构有限元模型Fig.4 Structure finite element model

3 结构动力特性分析

桥梁动力特性包括自振频率与对应的振型，它是桥梁结构固有的，可以反映桥梁的刚度指标，是结构动力分析的重要参数。 本文采用分块兰索斯法进行结构动力特性分析，结果如表1 所示（文中列出结构前五阶自振模态）。 第一阶、第二阶和第三阶振型图如图6～图8 所示。

图5 液压阻尼器与主梁的联系Fig.5 Relations of Hydraulic damper and girder

由表1 可知， 结构第一阶自振模态为主梁纵向移动。 这说明，主梁的纵向刚度最小，在动力荷载作用下，结构纵向最容易出现动力响应。 因此，需在桥梁上设置纵向限位装置， 以达到控制主梁位移和主塔内力的目的。

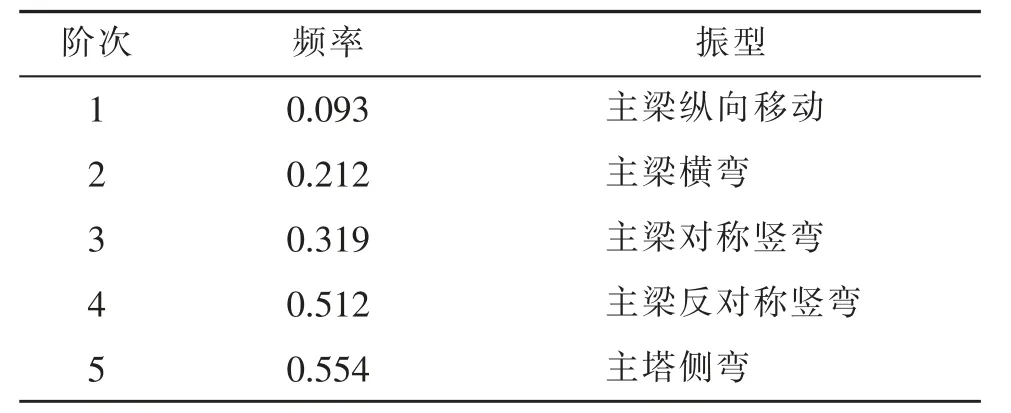
表1 自振模态Tab.1 Natural vibration mode

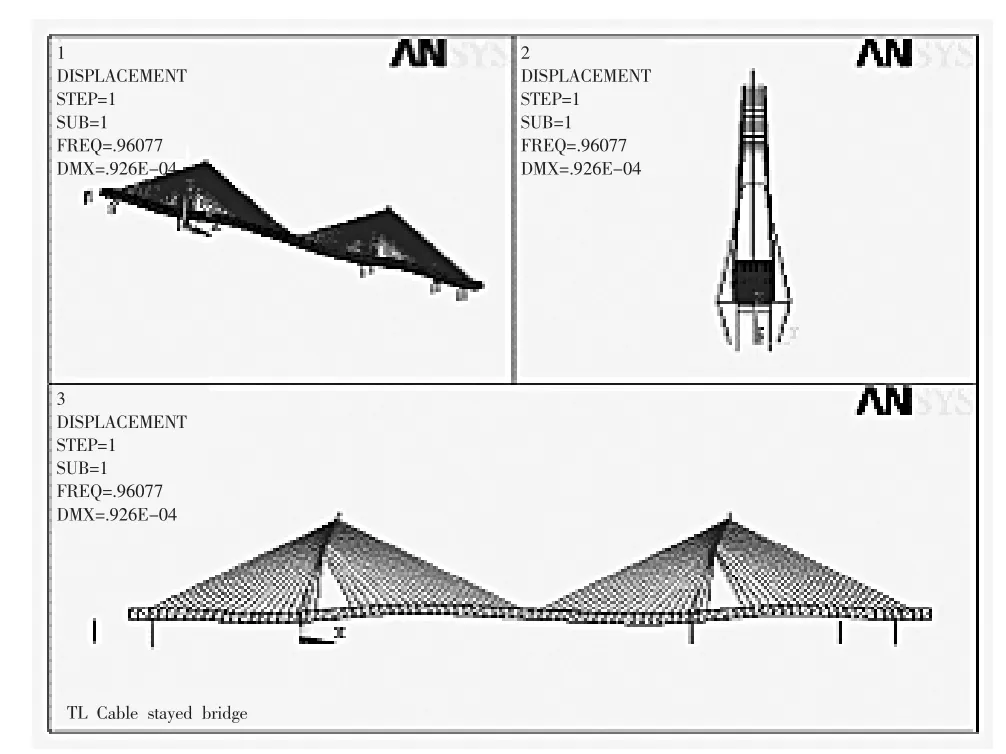
图6 第一阶振型图Fig.6 The first mode of vibration

图7 第二阶振型图Fig.7 The second mode of vibration

4 结构抗震分析

本文采用直接积分法对结构进行动力时程分析。结构自身阻尼采用瑞利阻尼输入，其表达式为式（2）。

［C］＝α［M］＋β［K］ （2）式中：α 为Alpha 阻尼；［M］ 为质量矩阵；β 为Beta 阻尼；［K］为结构刚度矩阵。

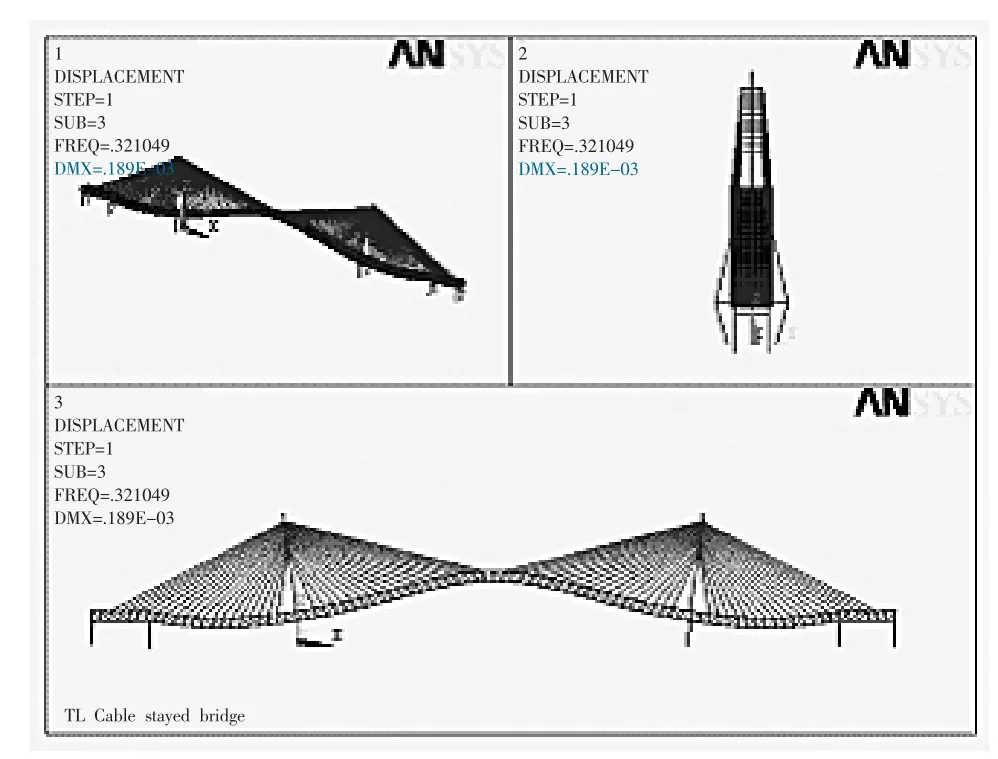
图8 第三阶振型图Fig.8 The third mode of vibration

采用时程分析法进行结构抗震分析时，通常输入地震加速度时间历程。在地震动特性中，对结构破坏有重要影响的因素为地震动强度、 频谱特性和强震持续时间等。地震动强度一般由地震加速度峰值来表示，频谱特性由地震加速度时程的主要周期表示。 鉴于场地类型，本文选取Taft 波、天津波与一组人工地震波来分析大桥地震响应。 为符合工程场区峰值加速度，对3条地震波做出相应修正，以满足其可靠性。

4.1 无阻尼器状态下结构地震响应分析

地震动时程分析采用Taft 波、天津波与一组人工地震波来进行， 并将地震波离散为以时间步为0.02 s 的加速度分布。 采用3 条地震波计算，响应结果取各关键位置的最大值。 地震动输入采用纵桥向＋竖向输入、横桥向＋竖向输入，竖向地震动加速度为水平向地震动加速度的0.6 倍。 计算结果如图9～图13 所示。

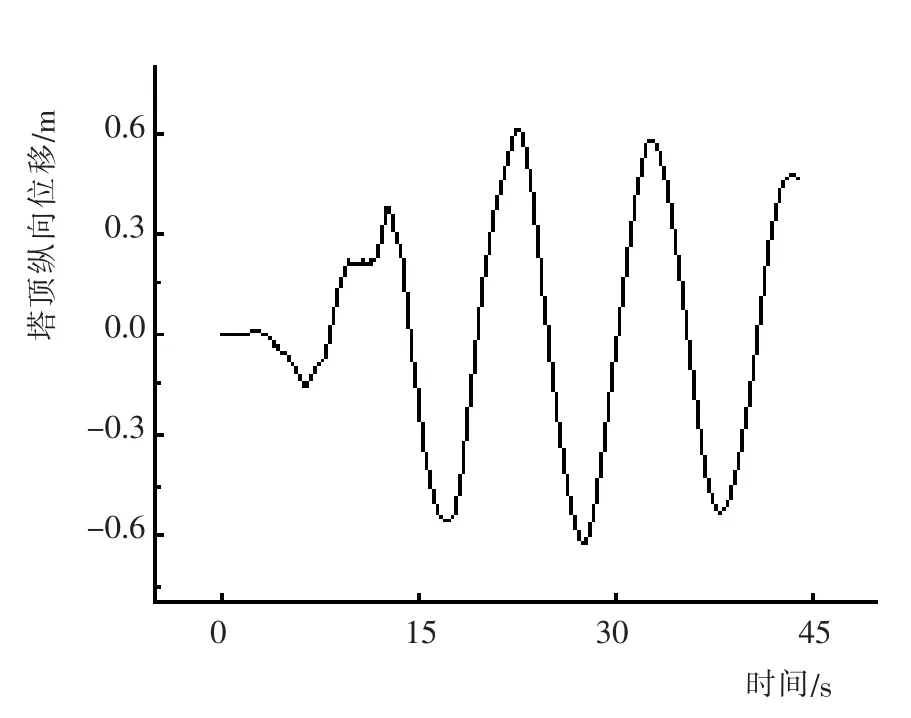
图9 塔顶纵向位移时程Fig.9 Longitudinal displacement time history of tower top

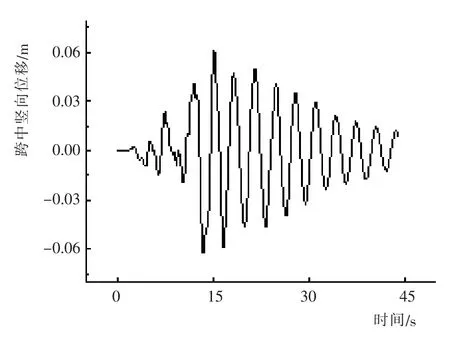
图10 跨中竖向位移时程Fig.10 Vertical displacement time history of midspan

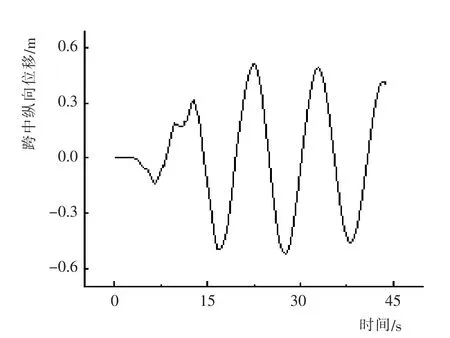
图11 跨中纵向位移时程Fig.11 Longitudinal displacement time history of midspan

图12 塔底弯矩时程Fig.12 Bending moment time history of tower bottom

由于桥梁结构属于长周期结构，在纵向激励下，主塔塔底内力主要由第一阶振型来控制， 其时程曲线波动周期约10 s，结构位移大，能量耗散速度慢。因此，为了合理控制结构位移和内力，需在结构纵向增设参数合适的液压阻尼装置来耗散地震能量，加快能量衰减速度。

图13 塔底剪力时程Fig.13 Shearing force time history of tower bottom

4.2 不同阻尼参数下结构地震响应分析

在地震动激励下， 液压阻尼器产生的阻尼力与阻尼系数和阻尼指数有关。 阻尼系数C、阻尼指数ξ取值不同，阻尼器对结构的影响也不同。如果阻尼器参数选择不当，耗能效果就达不到预期目标，甚至会出现相反作用。 本文主要对ξ＝1 时，阻尼系数C 值变化对结构地震响应变化的敏感性进行分析。 液压阻尼器阻尼系数C 值的选取如表2 所示。

表2 计算工况Tab.2 Working condition

采取Taft 波、天津波与一组人工地震波对该桥梁结构进行地震动时程分析， 获得在参数不同取值下桥梁结构关键位置的地震响应，再经计算分析，得出适用于本桥梁的阻尼器参数。图14～图17 为结构关键点和关键截面针对阻尼系数C 的响应趋势图。

4.3 分析对比

由图14～图17 可以看出，在液压阻尼器的介入下，主梁所承受的地震能量一部分转移到了桥塔上，桥塔结构承担了更多的地震效应， 从而减小了主梁的位移。由此可见，大跨度斜拉桥在塔与主梁之间设置纵向液压阻尼器， 可以有效地减小斜拉桥关键部位的位移，从而改善塔底、辅助墩和支座等关键部位的受力特性。

图14 主塔塔顶纵向位移Fig.14 Longitudinal displacement of main tower top

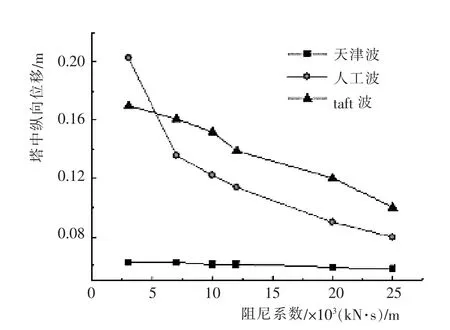
图15 跨中纵向位移Fig.15 Longitudinal displacement of midspan

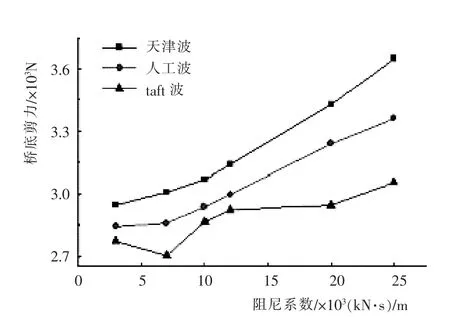
图16 塔底纵向剪力Fig.16 Shearing force of tower bottom

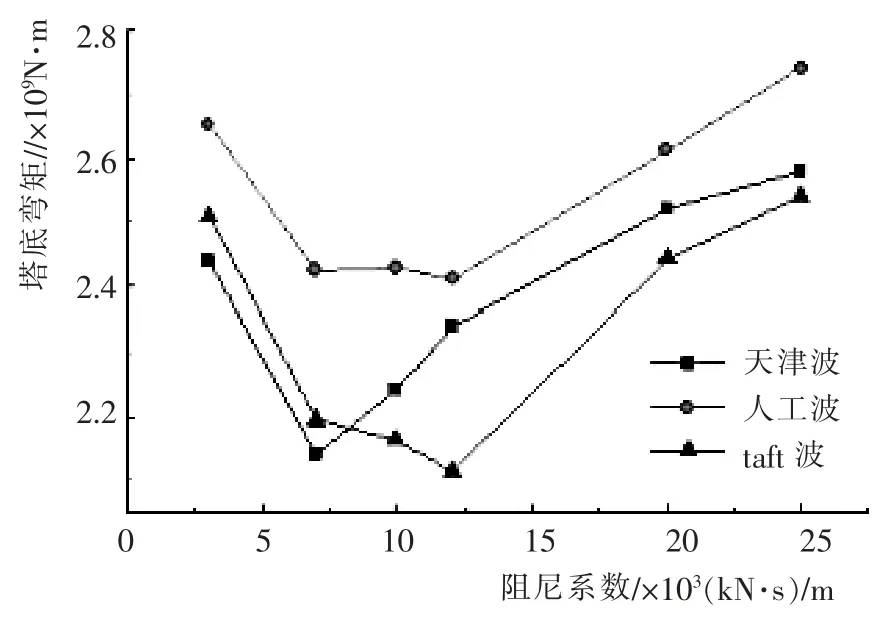
图17 塔底弯矩Fig.17 Bending moment of tower bottom

随着阻尼系数的增加， 桥塔塔顶的纵向位移和主梁跨中的纵向位移都逐渐减小， 桥塔底部的动力响应则逐渐增大。当阻尼系数为3 000～7 000 kN·s／m 时，塔顶、主梁位移下降幅度较大，塔底剪力上升趋势较为平缓， 主塔塔底弯矩也有明显下降。 当阻尼系数大于7 000 kN·s／m 时，塔顶、主梁位移下降趋势明显减小，且内力明显增大。综合分析， 选择阻尼系数为7 000 kN·s／m 的线性阻尼器，可以协调好位移与内力的关系，从而改善结构的抗震性能。

5 结语

对于大跨度斜拉桥，在塔梁连接处设置纵向液压阻尼器，可以来限制主梁的位移，改善结构的抗震性能。液压阻尼器阻尼系数为3 000～7 000 kN·s／m时，塔顶位移下降明显。 塔底剪力随着阻尼系数的增大而增大，塔底弯矩随着阻尼系数的增加会先出现一个明显下降阶段，而后再增加。 综合位移和内力的响应，可以认为，阻尼系数C＝7 000 kN·s／m 时，可以改善主桥的局部抗震性能。