基于渗流原理求解工程降水降落曲线的有限单元法

刘宜盈 赵 磊 李 冉

(烟台大学土木工程学院，山东 烟台 264005)

0 引言

对降落曲线的计算是计算基坑不均匀沉降的重要前提，基坑不均匀沉降严重时会造成周围建筑物的开裂、变形。因此精确地计算降落曲线对实际工程有巨大的意义。

对降深等水文地质参数的求解的办法有标准曲线对比法、直线图解法、试验法、切线法、微分图解法、积分图解法等。对于直线图解法李如刚[1]提出了对实例进行稳定流放水试验，用直线图解法和水位恢复法计算降深等参数；邹正盛等[2]依据最小二乘法建立自动配线法求解降深等参数，此类方法受到人为的影响较大，往往会产生较大的误差。

相较于图解法来说解析法更为简洁，李华等[3]提出利用对定降深井流条件下隐含待求参数的流量函数拟合替代和流量比值关系，通过整理推导获得了求解降深等相关水文地质参数的一元二次方程的解析法，但此类方法的工程量较大且测量误差较大。另外针对非稳定井流的研究大部分学者都是从Theis基本方程出发进行求解：如文献[4][5]的研究成果。稳定井流的研究则大都基于Dupuit公式，如文献[6]～[11]的研究成果。但是由于Dupuit公式没有考虑水流在入井时的水跃，因此在抽水井附近，实际漏斗曲线将高于Dupuit的理论曲线。

本文提出在渗流基本原理的基础上利用三角形相似求解稳定潜水井的基坑降水降落曲线的有限单元法：在稳定渗流场(在降水达到控制点水位时)中利用能量损失率最小原理，求解出该渗流域真实的水头分布位置，逸出点(降水后降水井井壁处的真实水位)的位置是确定的，因此可通过三角形相似求解该稳定渗流场在此状态下各处的逸出点位置，即降落曲线的位置。计算结果表明该方法有较高的计算精度，另外采用该方法可以考虑水头损失也弥补了裘布依公式未考虑水跃现象而导致误差的缺点。

1 求解降落曲线

1.1 能量损失率最小原理

对于满足条件的渗流域，求解渗流域中的水头函数可以引入以下泛函[12]:

(1)

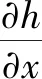
[K]{h}={f}

(2)

其中，[K]为n(未知节点水头的数量)阶总渗透矩阵;{h}为节点水头列阵;{f}为自由项列阵。求解此线性方程组，即可求得各节点的水头值，从而进一步计算降落曲线。

1.2 三角形相似求解降落曲线的方法

如降落曲线形成后，在曲线上下分为原水位线以上的无水部分、原水位线到降水后水位线之间的被疏干部分和降水后水位线以下的饱和土体。降水前水位线以上的土体没有经历降水的过程，因此其有效应力可视为不变，因此没有沉降的产生；降水后原水位线和现水位线之间的土体在降水历程中被疏干；降水后水位线以下色的土体在降水前后均位于稳定地下水位面以下，故而始终饱和[6,7]。在已知上游水位(降水前地下水水位)、下游水位(降水后降水井中的水位)以及渗出边界(水跃区段)求解降水区域内各有限单元中水头的分布，由逸出点(降水后降水井井壁处的真实水位)的位置出发，利用三角形相似求解该稳定渗流场在此状态下各处的逸出点位置，即降落曲线的位置[13-15]。

当水位稳定后，降水井水位低于井壁水位，地下水在入井时的流速造成的水头损失和入井后由水平运动转为垂直运动的损失，会产生水跃现象[16]，本文利用阿布拉莫夫经验公式[17]对水跃值Δh求解：

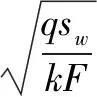
(3)

其中，q为单井排水量；F为面积，F=πdl(d，l分别为过滤器的直径和长度，m，m2)；A为与过滤器有关的系数(网状和砾石过滤器α=20，对缝隙和铁丝过滤器α=7)。

然后利用文献[18]的方法求解该渗流域的影响半径，确定渗流域的水平距离。对该渗流域进行有限单元划分如图1所示。降落曲线将渗流域划分为干区、湿区和过渡区，确定出过渡单元中过渡点的水位高度，将所有点连接起来即是降落曲线。

单独取出图1中被降落曲线穿过的单元，如图2所示，降落曲线穿越单元的节点自左向右，自上而下分别为1,5,6,10,11,14,15，设其水头及其位置水头依次为(hi,zi)(i=1,5,6,10,11,14,15)，降落曲线与三角形单元边长相交的节点，自左向右依次为(a,b,c,d,e)，其节点水头和位置水头依次为(hj,zj)(j=a,b,c,d,e)。即将求解降落曲线的问题转化为求解降落曲线穿越单元的节点(a,b,c,d,e)的水头，将这些点连接起来即是降落曲线。

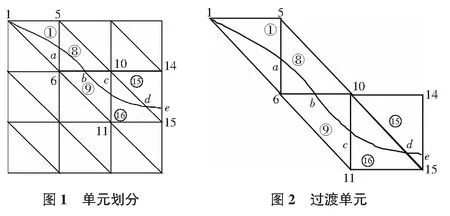
过渡单元可以分为两种类型：第一类是三角形单元中仅有一个节点在自由面以上，第二类是三角形单元中有两个节点在自由面以上。以第一类单元为例求解过渡点的坐标，用线性插值法求出降落曲线与三角形单元的交点坐标：设所求边的点为坐标点a，横纵坐标用(xa,za)表示,边两端坐标(端点坐标利用能量损失率最小原理计算所得)分别表示为(x5,z5),(x6,z6)。则a点坐标为：

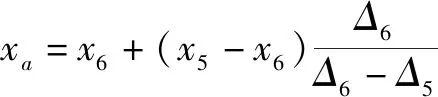
其中，Δ为水头与纵坐标差值(在降落曲线上的点差值为0)。在求解三角形三条边与降落曲线相交节点的水头时，求法是相同，因此可以用这种方法求出每一个过渡单元的每一条边上的降落曲线上的点。但是在程序编写过程中，筛选各边交点的方式不同[19]。这种方法在降水达到稳定时可直接定位出该逸出点状态下的整个降落曲线的位置。该法不仅具有计算量少且精度高的优点，而且不需要多次迭代。另外采用该方法可以考虑水头损失也弥补了裘布依公式未考虑水跃现象而导致误差的缺点。

2 工程算例

工程概况[6,7]。该地铁车站位于兰州市七里河区马滩村拟建工程场地，其基本概况为渗透系数取60 m/d，井成孔直径1 000 mm，管井直径800 mm，滤水管内径500 mm，滤水井管内采用天然圆砾填料。地下水位埋深约为8.5 m～9.1 m，深基坑深约为16 m。基坑降水单井涌水量约为800 m3/d～1 200 m3/d。本次勘察其各自的力学指标见表1中的建议值。

观测点分别命名为sw4，sw5，sw6，距离降水井分别为5 m，10 m，15 m。计算结果与裘布依方程的理论计算和实测值对比。在sw4，sw5，sw6观测点本文计算结果与实测值的相对误差分别为-3.0%，-5.7%，-6.9%，理论计算结果与实测值的相对误差分别为-9.6%，12.1%，12.8%，结果表明文计算方法得到降深的结果与实测值更接近。

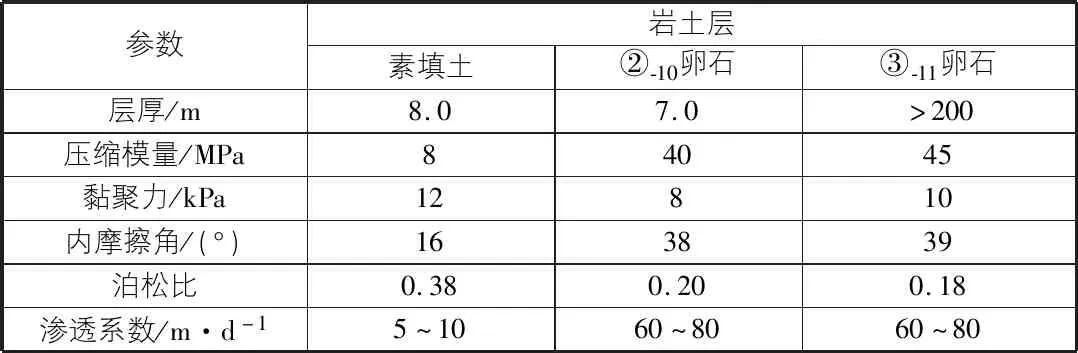
表1 拟建场地岩土层的物理力学参数

3 结论

本文在渗流基本原理的基础上提出利用三角形相似求解稳定潜水井的基坑降水降落曲线的有限单元法。利用本文建立的计算方法计算了实际工程案例，得到的水位降深值与理论计算值和实测值作了对比，得到如下结论：

1)在稳定渗流场(在降水达到控制点水位时)中利用能量损失率最小原理，求解出该渗流域真实的水头分布位置，逸出点(降水后降水井井壁处的真实水位)的位置是确定的，因此可通过三角形相似求解该稳定渗流场在此状态下各处的逸出点位置，即降落曲线的位置。

2)该法不仅具有计算量少且精度高的优点，而且不需要多次迭代。