基于灰色—马尔科夫模型的高边坡变形预测应用
莫 文 涛
(郑州工业应用技术学院,河南 郑州 451100)
0 引言
高边坡稳定性和路面设施、行人、行车的安全性具有密切关系,边坡安全监测能够将被监测区域在不同时间的情况及时反映出来,以此为边坡现状分析和状态预测提供根据。目前,在高边坡位移变形预测过程中的方法包括回归预测与人工预测模型,此预测方法会陷入到局部极值,并且需要大量样本对预测精度保证[1]。为了降低预测误差,本文和具体工程预测数据结合,使用灰色—马尔科夫模型实现高边坡变形的预测。
1 灰色—马尔科夫模型分析
1.1 灰色GM(1,1)的模型
灰色量为位移监测数据,能够得出灰色序列,使用一阶微分方程GM(1,1)模型,通过实际数据生成的GM(1,1)模型白化响应公式为:
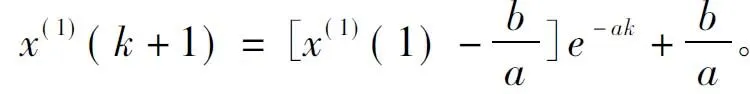
其中,a为发展系数;b为灰作用量。
根据原本的样本规律能够产生灰色GM(1,1)模型预测值,实际预测值并不会受到原本样本影响。以此,在实现动态预测过程中添加状态步数与转移,使用马尔科夫预测模型使灰色模型不足进行弥补[2]。
1.2 马尔科夫预测方法
马尔科夫为根据目前事件状态对未来时间段状态预测的模型,涉及到状态、状态转移与相应马尔科夫过程相应的概念。灰色—马尔科夫模型的创建步骤为:
1)状态划分。根据灰色GM(1,1)模型对预测值和实测值相对误差序列进行计算,以此划分h个状态区间:
Ei=[Ai,Bi](i=1,2,…,i)。
2)通过状态Ei经过k步到状态Ej转移的次数为nij(k),出现状态次数为ni,那么状态Ei通过k步到状态Ej中转移的概率为:
此模型转移概率和初始状态没有关系,n×n阶状态转移概率矩阵为:
3)h步状态转移概率矩阵为第一步状态转移概率矩阵h次方,也就是:
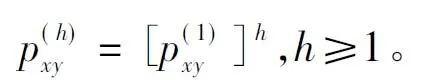
以此,灰色—马尔科夫模型中的GM(1,1)模型没有考虑动态转移因素,步数调整、状态转移使模型预测过程满足边坡位移真实情况,从而弥补灰色GM(1,1)的模型问题,降低模型固有误差,使长期预测精度得到提高,增加了有效预测时间[3]。
2 工程实例
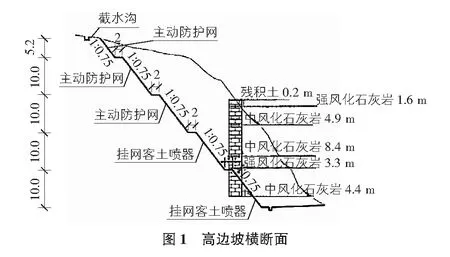
贵州省某高速公路工程的高边坡,此段边坡长度为551 m,通过人工开挖高边坡设计线路,最大开挖高度设计为155.43 m,属于十级边坡,每级高度为15 m。1级~3级坡比为1∶0.3,4级~10级坡比为1∶0.5,每级平台的宽度设置为2 m,7级和4级设置5 m宽度平台,开挖全坡面实现锚杆挂网喷射混凝土的防护设置,锚杆长度为9 m,间距设置为2 m,破碎1.5 m。在边坡开挖支护施工过程中,边坡临空面增加,坡体坡面破碎带,溶洞发育、隐伏裂隙,并且在开挖局部坡面之后会出现拉裂变形、塌方掉块的情况,坡面岩体的结构变化差异比较大。边坡一共设置5个测量基准点与32个监测点,一共监测63次,每周2次[4]。图1为高边坡横断面。
3 预测结果
3.1 灰色模型预测的结果
以工程坡顶水平的位移实际测量数据,在坡顶设置两个点,表1为GM(1,1)预测值和相对误差,基于GM(1,1)模型实现水平位移变形预测,白化响应式解围:
x1(t+1)=104.126 3e0.047 5t-102.126 3。
x0(t+1)=x1(t+1)-x1(t)。
通过累减还原之后得到预测数列:
x0(t+1)=4.830 4e0.047 5t(t≥1)。
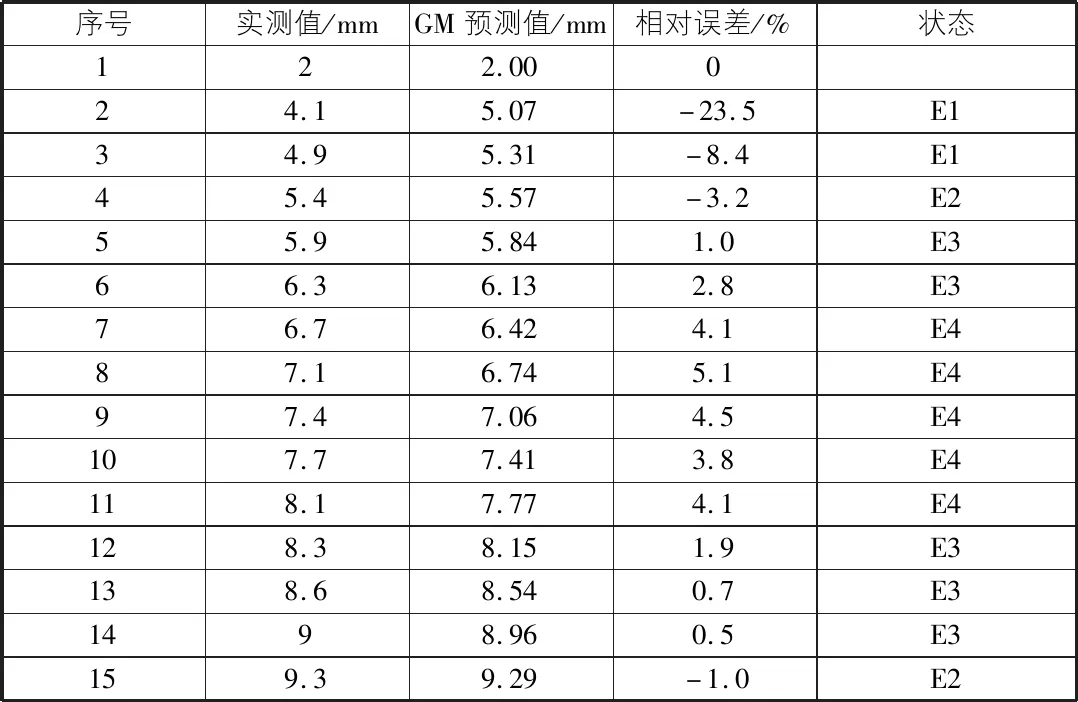
表1 GM(1,1)预测值和相对误差
通过表1表示,GM预测值与边坡实测位移值的最大和最小误差分别为23.5%,0.5%,平均精度为95.5%。由于前期存在明显的开挖扰动,所以其相对误差比较大。表示GM(1,1)模型能够利用原始离散数据对系统未来的发展精准预测,提高整体的预测精度[5]。
3.2 灰色—马尔科夫模型的预测结果
灰色—马尔科夫模型充分考虑概率问题的未来发生情况,将灰色理论作为基础提出了修正系数。以灰色理论时间序列结果,能够得出边坡位移的监测预测值:
x0(t+1)=β4.830 4e0.047 5t。
β=1+θ。
其中,β为修正系数;θ为预测状态区间中值。以灰色—马尔科夫模型的划分原则,使误差值划分成为[-24,-5],(-5,0],(0,3],(3,6],表2为各状态下的β值。

表2 各状态下的β值
基于灰色理论预测值、实测值和精度分别为10.33 mm,9.9 mm,95.7%,灰色—马尔科夫转移模型预测值和精度分别为10.07 mm,98.3%,以此得到表3的预测值和相对误差。

表3 预测值和相对误差
通过表3表示,GM-MC模型在高边坡变形监测过程中的使用误差最大为5.7%,平均精度在98.1%以上。数据离散型在边坡监测前期较大,开挖扰动还会对其造成影响,灰色理论预测结果的精度低,预测的结果和实测值相互接近。结果表示,灰色—马尔科夫模型应用到高边坡变形预测中具有良好的效果[6]。
4 结语
边坡开挖属于动态化过程,由于施工前期具有较大的扰动,边坡现场监测的水平位移离散性比较大。灰色—马尔科夫模型充分考虑动态转移概率,所以能够应用到开挖变形预测中。通过本文研究表示,本文所设计灰色—马尔科夫模型的预测精度较高。

