基于间隙补偿的线束直径估算方法研究

韩占朋，谭 磊，王业冉，穆晓敬

（航空工业洪都，江西 南昌，330024）

0 引言

在电缆设计及布线过程中，需使用布线器件进行安装及保护，而在飞机系统布线中，通常采用电缆卡箍作为主支撑件，且间隔距离不得大于600mm[1]。卡箍的选用以线束的直径为主要依据，过大或过小，固定不牢或夹伤线束，均会影响电气连接可靠性。而卡箍常常在飞机制造过程中预先固定在结构上，后续更换及维护困难，部分区域甚至不可达，无法维护。另外，线束直径对设计线束通路及口框具有指导意义,因此，准确估算线束直径十分重要。由于线缆卡箍的尺寸以1mm为基数增长[2]，因此线束直径的估值误差在1mm内是较为满意的。

目前常用的线束直径估算方法有经典计算法、等效正方形法及航标中给出的参考公式[3]。经典计算依赖于经验系数，对于系数缺失的电缆组合直接估算偏差较大，等效正方形法将电缆等效成正方形进行面积加和来估算线束直径，估算值一般较实测值偏小，而航标参考公式计算结果偏大，必须进行修正，无法直接使用。

本文通过对线束建立截面数学模型，提出一种基于间隙补偿的线束直径估算方法，结合实例对比计算，验证了算法的有效性。

1 数学模型

典型线束由不同规格的电线组成，成束后一般捆扎为圆形，由于电线排列方式多样，直接估算其直径D比较困难。首先简化模型，计算同规格电线（直径d）组成的线束直径。

基于工程实际使用情况作如下假设：

1）电线的横截面为刚性圆周，不可变形或变形可忽略。

2）成束的线束为正圆或近似正圆。

3）电线在线束中分层排布。

4）线束直径由排布到最外层的电线数量决定，且数量一般为整数。

典型线束截面如图1左图所示。

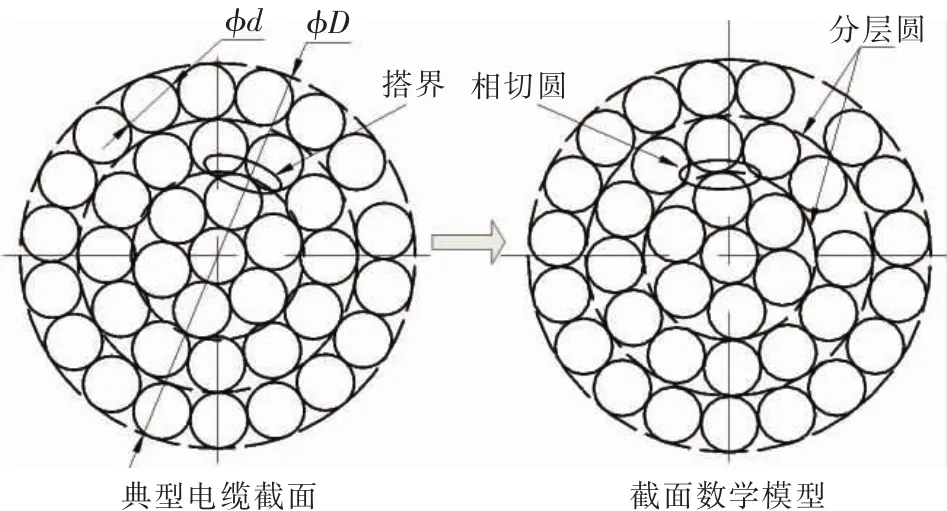
图1 电缆集束图示

左图中有且仅有第2层与第3层电线之间存在搭界 （即分层圆与电线非相切）。为便于计算，建立图1右图所示的截面模型，使模型中电线与分层圆相切。

根据图2所示几何关系，所建模型与典型截面的建模误差约为0.07d。

图2 模型误差分析

由于模型中电线与分层圆相切，因此可方便的计算出电线的包裹间隙，得到线束的截面积及半径，然后依据外层电线为整数的特点二次逼近线束直径。

2 间隙补偿算法

2.1 算法描述

根据已知条件计算所有电线的截面积之和：

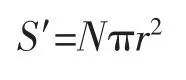
其中r=d/2，N为电线的数量。

线束的近似半径如下：

集束后的线束由于存在包裹间隙，计算值R′远小于实际值。因此要估算线束直径需进行间隙补偿计算。典型单根电线的包裹间隙如图3中的阴影所示：

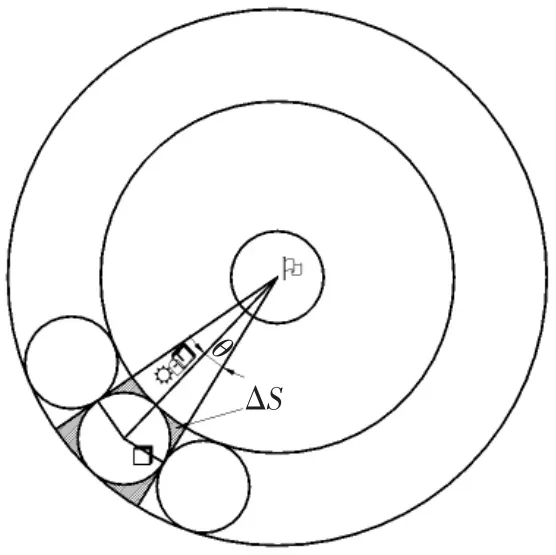
图3 典型电线包裹间隙

其阴影面积ΔS计算如下：

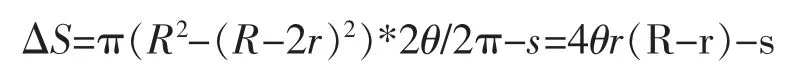
式中为电线对应线束圆心的角度，θ=arcsin（r/R-r）θ∈（0，π/2)；s为电线截面积s=πr2。

根据上式，当R≫r时有下述关系：

此时包裹间隙等于正方形面积与电线截面积的差值，即为等效正方形法，因此等效正方形法的计算结果应小于间隙补偿算法，且其计算结果应小于实际直径。

由于R为未知量，可用近似计算ΔS。

可以证明线束中均摊到每根电线的间隙不小于最外层电线的间隙ΔS，证明如下：

外层电线的包裹间隙为 ΔS1，半径R1，弧度 θ1，次外层电线的包裹间隙为 ΔS2，半径R2，弧度 θ2，且有θ2＞θ1，R2≤（R1-2r），如图 4 所示。

图4 包裹间隙计算

则有：

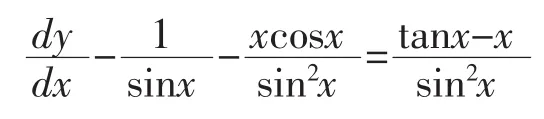
上式函数曲线如图5所示，因此dy/dx成立，在（0，π/2）区间内，y为单调递增函数，进而可知 Δδ＜0，因此线束中均摊到每根电线的间隙不小于最外层电线的间隙成立。

图5 函数曲线图

另外根据图5可知，当Δθ较小时，Δδ的增量比较小，因此电线总的包裹间隙可以近似为NΔS。

综上分析，线束截面积S有如下关系：

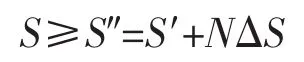
由于最外层的电线数量nm∈Z+，则有：

其中roundup为向上取整。

则捆扎成束后的线束直径计算如下：

2.2 算法与模型符合性验证

对上述算法与所提数学模型的符合验证如下：

根据数学模型对直径为1.5mm的1到15根的同规格电线进行排布，排布分层及线束直径如图6所示：

采用间隙补偿算法进行计算，结果见表1。

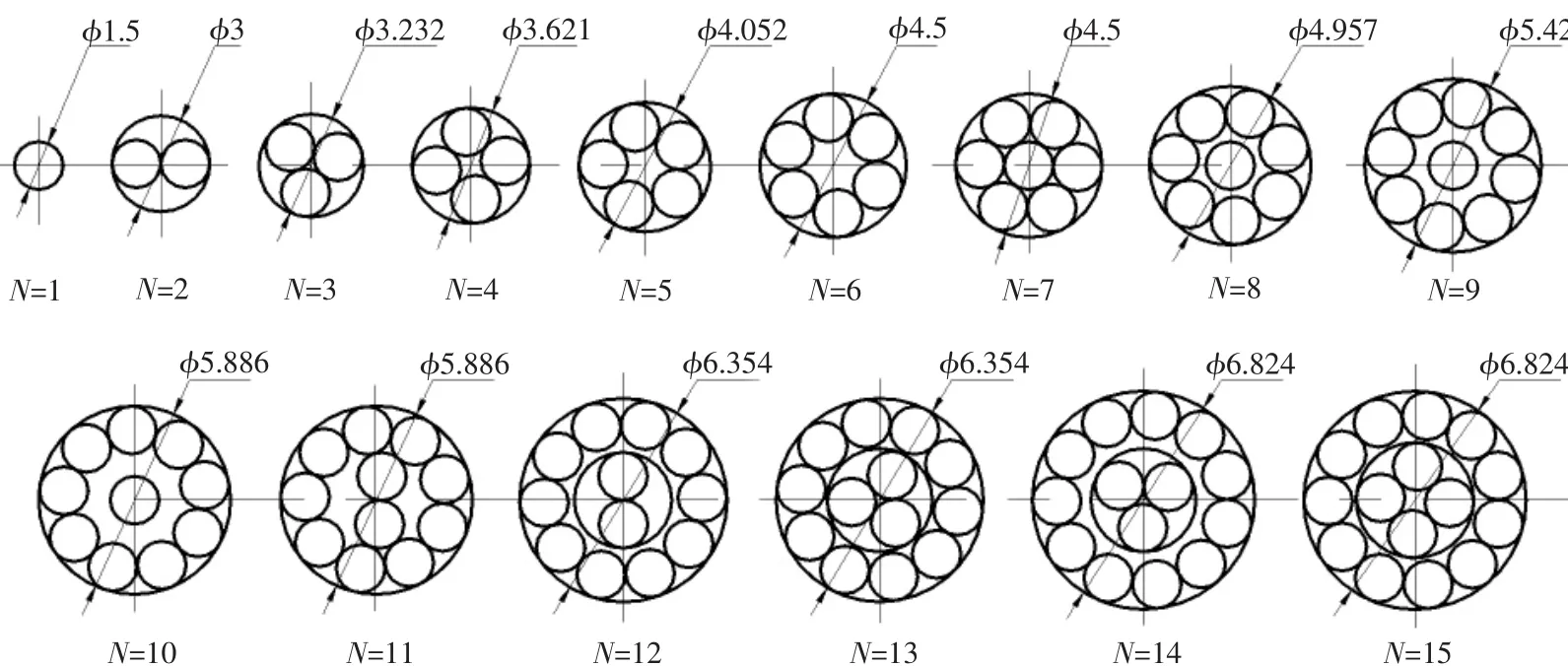
图6 电线排布

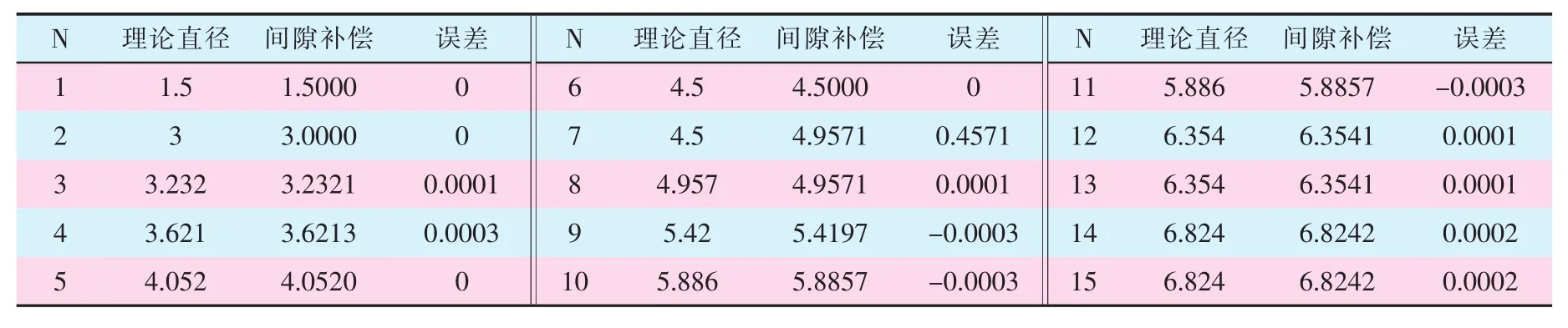
表1 模型验证 mm

从表1可以看出：间隙补偿算法与模型理论值基本一致。仅当N=7时，出现较大误差，这是由于电线数量增加而实际线束直径没有变化，而算法只关注最外层的电线数量，导致个别点的误差增大，但依然在容许范围内。

基于以上分析，所提算法能有效估算线束模型的直径。

3 线束直径估算

在实际使用中，电缆由不同规格的电线组成，每种规格的电线直径为di，数量为ni，且n1+n2+n3+…nm=N。对于不同直径的电线其包裹间隙计算如下：

则线束截面积S有如下关系：

式中req为等效半径，计算如下：

令最外层电线的数量n∈Z+，则有：

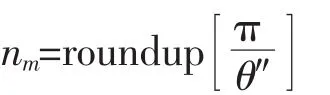
则捆扎成束后的线束直径计算如下：

4 实例分析

从飞机系统实际使用情况出发，以全信QLA系列传输线[4]为例，实测不同规格的电线组合而成的线束直径，如表2所示。

表2 组合电线线束直径 mm

采用经典计算法、等效正方形法及所提算法进行对比计算，计算结果如表3所示：

表3 计算结果 mm

计算结果与实测直径的误差如图7所示：

图7 实测误差曲线图

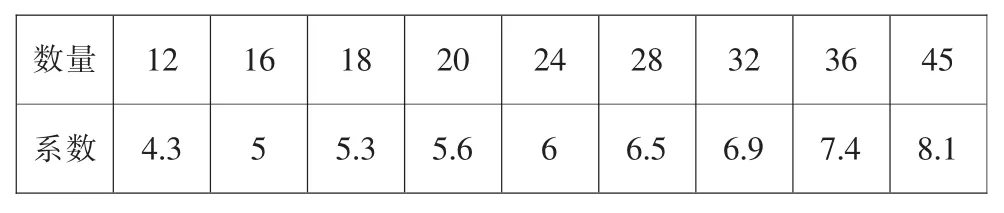
1注：拟合系数根据现有数据采用10阶多项式拟合后得到。部分数据如下表所示：

根据结果分析如下：

经典算法误差最大，约为±1.5mm，且对同规格电线组成的线束（1、3、6组）计算值较实测值偏大，误差在 0.5～1.5mm 之间，而组合电线线束（2、4、6、8 组）计算值较实测值偏小，误差在-0.5～-1.5mm之间。第5组由于QLA10811-24的数量远大于其他规格电线，使其误差折中后最小，约为0.15mm。并且，经典算法十分依赖经验系数，使用经验系数（1、3、7组）计算的结果明显优于拟合系数1（2、4、6、8 组）。

等效正方形法计算值均偏小，误差在0～-1.5mm之间，这与第2节的分析相吻合。同规格电线线束（1、3、6组）的计算误差相对较小，且呈现出与电线直径正相关的关系：直径越小，误差越小。可以预测计算误差会随着电线直径的增大而增大。而组合电线的线束误差相对较大，基本在1mm以上。同样受QLA10811-24的影响（数量多，直径小），第5组误差优于其他组合方式（2、4、7、8 组）。

间隙补偿算法的结果最优，基本在零线附近波动，最大误差0.75mm。对于同规格电线线束，计算误差相对较小（1、3、6 组），基本取上差（0～0.5mm），且大于0.07d。说明所建模型与实际直径存在差距，主要是由于电线具有一定的变形量，实际包裹间隙略小于计算值。对组合电线线束，计算误差略有增大（2，4，5，7，8），且基本取下差（-0.5～-1mm）。 这是由于所提算法并未关注不同规格电线之间的间隙，而实际间隙略大于单根电线的间隙值。

5 结论

线束直径的估算有利于电缆通路设计及支撑件的选型，本文通过建立线束截面模型，提出一种基于间隙补偿的线束直径估算方法。实例分析表明所提算法优于经典计算及等效正方形法，对于任意组合的电线线束均能得到较为满意的结果。