机载设备外场可靠性评估方法

涂美霞，王二振，雷长春，黄轶华

（航空工业洪都,江西 南昌，330024）

0 引言

随着对航空武器装备可靠性要求的提高，可靠性和性能被置于同等重要的位置，因此，对可靠性评估方法的科学性和结论的准确性提出了更高要求。根据可靠性指标评估过程，可知主要影响评估准确性的是评估模型和评估时间。目前相关的国军标可靠性评估方法采用基于指数分布的区间估计模型和点估计，一般认为试飞阶段产品已处于故障偶发阶段，故障率趋于恒定。然而，在试飞阶段的某些产品的软硬件技术状态没有固化，可靠性处于不稳定状态；另外，部分产品的早期故障还存在，经设计改进，可靠性呈增长趋势。因此，试飞阶段可靠性评估选用基于指数分布的模型不准确。在可靠性评估时间上，以往型号外场可靠性评估将空中工作时间和地面工作时间按1：1相加。对大量飞行试验数据分析，机载产品在空中和地面两种工作环境中，所受应力不同，其故障率表现不同，因此将空中工作时间和地面工作时间按1：1相加不合理。为了解决上述问题，本文结合AMSAA模型特点作为评估模型和引入环境因子处理评估时间，提出了一种机载设备外场可靠性评估方法。

1 方法介绍

在外场可靠性评估中，借助AMSAA模型模拟机载设备的寿命分布，使其更加适合外场产品的技术状态，并引入环境因子进行产品空中时间和地面时间数据的折合，从而计算得出机载设备的可靠性评估指标即平均故障间隔时间MTBF。

1.1 故障数据记录

获取飞行试验的某种机载产品责任故障数r，并统计分析出空中发生责任故障数r1和地面责任故障数r2；其对应故障发生的时刻为t1、t2…t3；故障发生时刻该机载产品在空中工作时间分别为t11、t12…t13；该机载产品空中工作时间为T1和地面工作时间为T2。

1.2 环境因子K

为了考虑空中和地面工作环境不同对产品的影响，本文采用理论公式计算方法，来确定环境因子K。该计算方法基于以下三个假设条件：

1）在不同的环境应力水平下，产品的失效机理不变；

2）在不同的环境应力水平下，产品的寿命服从同一分布；

3）产品的残存寿命仅依赖已累积失效和当前环境应力，与累积方式无关。

在外场，设机载产品空中工作时间和故障为（T1，r1），地面工作时间和故障为（T2，r2），当置信度为C0时，环境因子K：

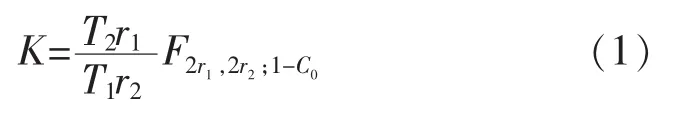
式（1）中，F2r1，2r2；1-C0是自由度为 2r1，2r2和C0的分布函数。

当空中和地面至少有一个为零故障时，假设如下：

1）当空中没有发生故障时，假设r1=1，工作时间设为3T1；

2）当地面没有发生故障时，假设r2=1，工作时间设为3T2；

在外场试飞中故障为零的情况有三种，根据上述两种假设，利用公式（1）计算出不同情况下的环境因子计算公式，见表 1。

表1 零故障情况下环境因子计算公式

1.2 数据折合

引入环境因子K后，计算平均间隔时间（MTBF）时，要将空中工作时间折合到地面工作时间，其转换公式为：

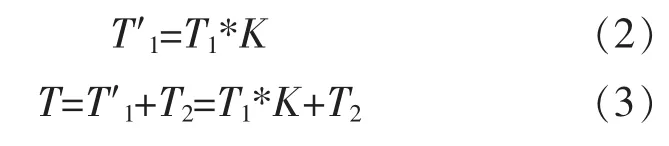
故障发生的时刻为t1、t2…t3；故障发生时刻该机载产品在空中工作时间分别为t11、t12…t13，则经环境因子K折算后的故障发生时刻：

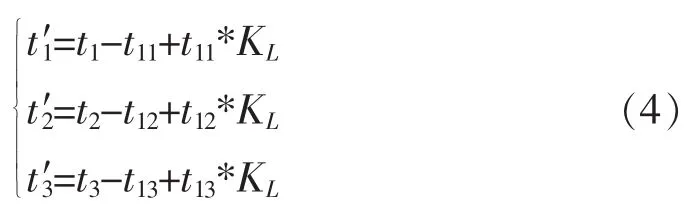
1.3 MTBF的评估

外场中，某些设备的技术状态没有固化，另外，部分产品的早期故障还存在，对出现的故障采取有效的纠正措施，其可靠性呈增长趋势。本文引用AMSAA模型来描述可靠性增长趋势。

AMSAA模型与指数分布模型中故障率是恒定的不同，AMSAA模型的故障率与时间有关，见式（5）：

式（5）中：a—尺度参数；b—形状参数

由式（3）可知该机载产品总的工作时间为T。在此期间，发生了责任故障数r。经环境因子K折算后的故障发生时刻：t′1，t′2…t′r， 则 AMSAA 增长模型的r个故障发生的时刻t′1，t′2…t′r联合分布函数为：

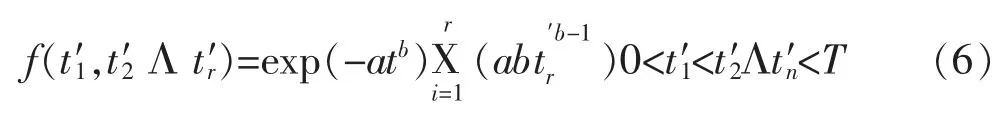
因此，T时刻该机载产品的可靠性评估值是

结合T=T1*KL+T2，则：

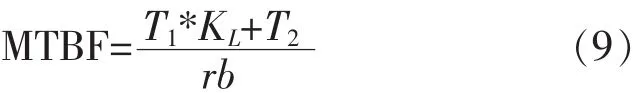
2 算例

上述实施算例中的数据都为外场试验统计数据。下面给出一个具体的算例：

某机载产品在外场试飞中的空中工作时间和故障，地面工作时间和故障的记录情况见表2。故障发生的时刻为 20h、116h 和 262h，记为t1、t2和t3；其对应故障发生时刻机载产品在空中工作时间分别为0h、20h 和96h，分别记为t11、t12和t13。

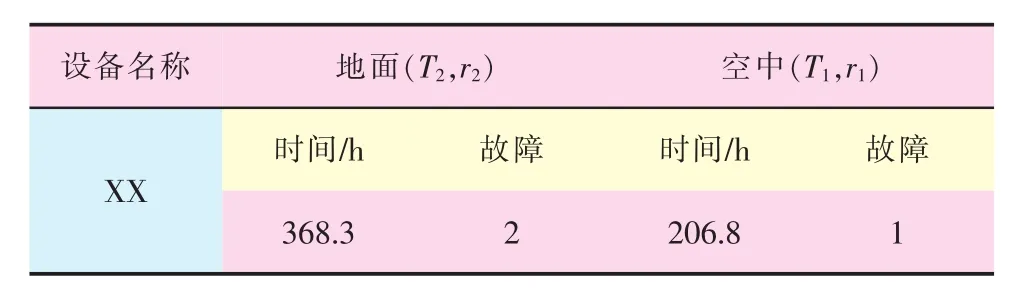
表2 某机载产品的故障信息

当置信度为C0=0.8时，按照式（1），则环境因子K：

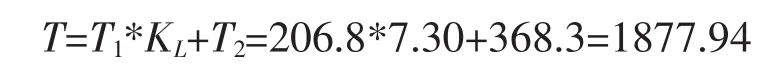
计算该机载产品的平均间隔时间（MTBF），要将空中工作时间折合到地面工作时间，则其总工作时间T：根据将空中工作时间折合到地面工作时间的T=T1*KL，按照式（4），得环境因子K折算后的故障发生时刻分别为：

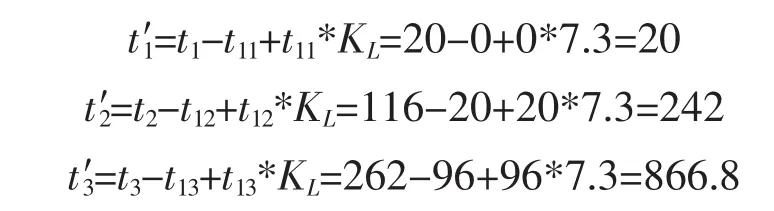
本文引用AMSAA模型来描述该机载产品寿命分布，AMSAA模型的故障率与时间t有关，结合折算后的故障发生时刻及故障数，按照式（7）和式（8）得到尺度参数和形状参数：

因此，T时刻该机载产品的可靠性评估值MTBF：

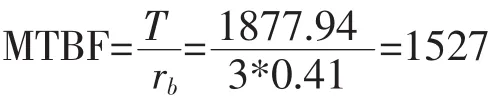
3 结论

在机载设备外场可靠性评估中，考虑设备的技术状态没固化，处于增长模式，故通过AMSAA模型来模拟可靠性增长并引入环境因子进行工作时间数据折合，使得可靠性模型更加科学，评价结果更准确。