一个和型不等式的定积分证明与思考

◇ 广东 孙传平

1 题目

(1)若函数f(x)在x=0处有极值,求函数f(x)的最大值;

(2)是否存在实数b,使得关于x的不等式g(x)<0在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由;

本题前两问比较容易,第(3)问有一定的难度.本文先给出第(3)问的定积分证法(此问证法不唯一,笔者认为定积分证法较为简捷)，再进行反思与拓展.

2 解法探究

证明(3)先证右边，当n=1时,右边不等式中等号成立;

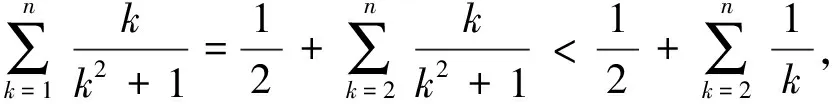
①

即

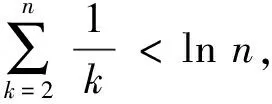
②

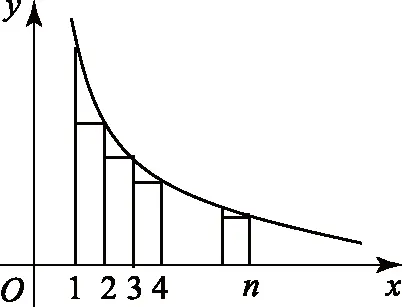
图1

由①②,得

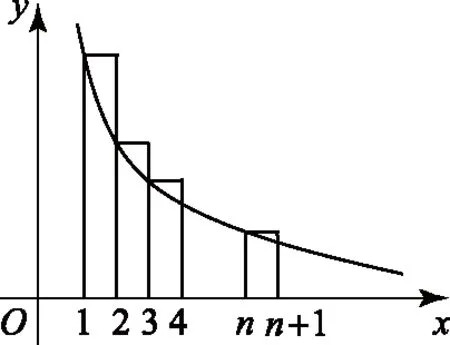
图2

由区间[1,n+1]上的n个矩形的面积之和大于曲边梯形的面积,得

即

③

综上所述,原不等式成立.

3 解后反思

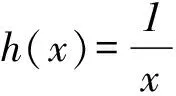
2)右边不等式的证明过程中有一个步骤

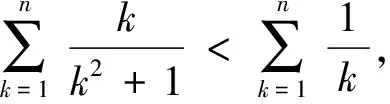
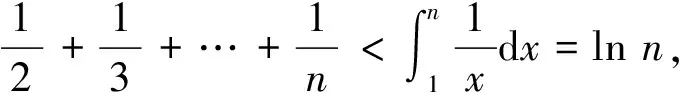
所以

④

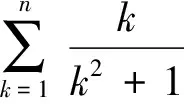
4 拓展

导数应用题中出现和型不等式的证明,并以此压轴的现象在高考数学试题和各地模拟试题中正悄然升温.

(1)用a表示出b,c;

(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;

由S1>S2,问题易得证.

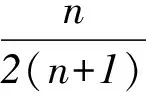
运用定积分证明和型不等式是高中数学课程中定积分应用的一大模块,它思维起点低、思路清晰、操作简便直观,更难得的是它解决问题的普遍性.有关此类和型不等式的证明,一般都可以采用这一方法,因而成为我们破题的好帮手.此法甚好,不过要想做到驾轻就熟,还须注意:① 合理构建“理想函数”h(x)(必要时先放缩后构造);② 选准用于分割区间的图形的形状(矩形或梯形);③ 若有放缩法参与,还要注意控制放缩的“步伐”.