两本教材例题数量与类型的研究
张港

[摘 要] 五年制高职的学生学习数学存在一定困难。一方面,数学基础不扎实,底薄并伴随着某种程度的厌学情绪。另一方面,尽管数学学习的内容较多,进度较快,但学校分配的教学时间却显得不足,甚至为了给专业课提供更多的时间而挤压数学课程的学习时间。在这种情况下,教师应该思考,如何在有限的时间内取得更好的效果。首先,针对例题教学,要搞清楚例题的浅层结构和深层结构[1]。浅层结构包括例题的类型、数量和素材,深层结构包括例题的处理方式、基础性、典型性和示范性。
[关 键 词] 例题;数量;类型
[中图分类号] G712 [文献标志码] A [文章编号] 2096-0603(2020)13-0124-02
蘇教版数学第一册是根据教育部2009年颁布的《中等职业学校教学大纲》和江苏省教育厅2009年印发的《江苏省五年制高等职业教育数学课程标准》编写。北大版《五年制高职数学》第一册是根据《五年制高职数学课程教学基本要求》,在2005年第一版的基础上修订而成。
在教材内容方面,苏教版教材注重知识的来龙去脉和知识在实际生活中的应用,重视培养学生利用所学知识分析问题和解决问题,注重培养学生的发散思维和创新能力。北大版教材内容由浅入深,循序渐进,通俗易懂,没有烦琐的推理和证明。由于苏教版的数学教材共七册,而北大版教材共三册,所以每册的内容有所不同,只研究两版本教材第一册中共同的部分。由于北大版教材的第一章是集合与不等式,而苏教版的第一章是集合,第二章是不等式,为方便比较,将苏教版第一章和第二章并为第一章,后面三章依次向前提一章。
例题数量的比较在统计苏教版教材和北大版教材的例题时,采用以下原则。两版本在例题的标号上是一致的:大题用例1,例2,例3…编号,小题用(1)(2)(3)…编号。本研究约定:数量按小题的个数计算。
例:下列对象能否组成集合?
(1)中国的直辖市; (2)方程x2-1=0的所有解;
(3)大于3的自然数; (4)著名科学家[1]。
此题按4个题计算。
一个题有多问的,按一个题计算,比如:已知扇形周长为20cm,当扇形的圆心角为多少时它的面积最大?最大面积是多少[2]?
一、例题数量的比较
从图1中可以得到,第一章苏教版65题,北大版33题,相差较大,近32题,前者的数量几乎是后者的二倍。由于苏教版将第一章划分为9节,而北大版只有5节,苏教版例题较多。第二章苏教版和北大版例题数量分别是37题和23题,尽管苏教版的习题仍然较多,但低于北大版的二倍,而且苏教版比北大版多了一节函数的实际应用,也导致苏教版的例题数量较多。第三章苏教版61题,北大版39题,两者相差22题。原因有两个:一是苏教版划分得更加细致,将实数指数幂和幂函数分为两节,而北大版将二者合为一节,对数划分为3节,共9节;二是苏教版多利用计算器求对数值和指数函数、对数函数的应用这两节。第四章苏教版48题,而北大版73个例题,可见北大版在第四章设置了更多的例题,反映出编者对第四章的重视。总体而言,苏教版的例题数量仍然超过北大版的例题数量。
苏教版第一册包含了集合与不等式、函数、幂函数、指数函数与对数函数、三角函数。课程标准中规定课时数为50课时(集合与不等式12课时,函数、幂函数、指数函数与对数函数22课时,三角函数16课时)。从图中可以算出每课时例题量分别为:苏教版4.22题,北大版为3.36题。比较而言,苏教版比北大版多0.86题/课时。然而,已结束学课中,多少例题才是最恰当的,目前仍然没有定论。
二、例题类型的比较
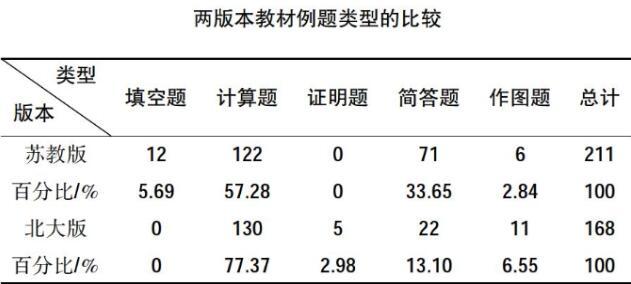
【统计方法说明】按题号进行统计,判断,大小比较,叙述等都归入简单题。
在例题类型方面,从上表中可以得到,两个版本的教材例题的题型都是传统题型,创新不足。
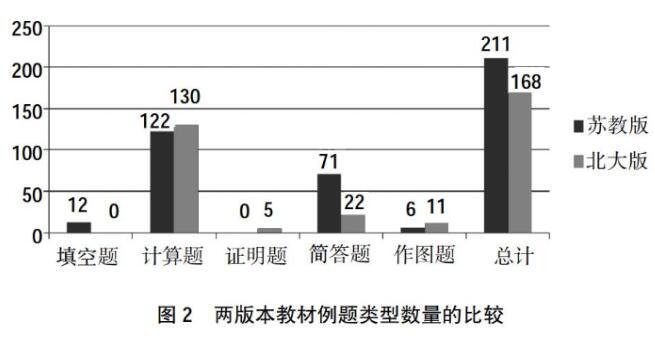
从图2可以看出,两版本的例题的选择有共性,也有区别。苏教版和北大版教材都注重计算题和简答题,都涉及一些作图题,但对待填空题和证明题则有明显的不同,这从每种题型所占的比例图中体现得更明显。
从图3中可以得出,苏教版和北大版都重视计算题,简答题,有少量的作图题。两版本的区别也很明显。相比苏教版,北大版教材更重视计算题,占比达77.37%,比第二位的简答题多了近64个百分点,占比排第三位简答题的占比只是6.55%,没有填空题。苏教版教材的例题尽管计算题占比也是最大,达到57.82,占比第二的是简答题,占比33.65,两者相差近24个百分点,含有少量的填空题和作图题,没有证明题,苏教版各种题型较为均衡,苏教版则相差悬殊。
证明题可以培养学生思维的严谨性和周密性,苏教版中缺少证明题,可以说是一种缺失,对作图题的重视程度也不够,不能很好地体现数形结合这一重要数学思想。
参考文献:
[1]卢萍,邵光华.中德代数教材例题特色比较及启示:以“指数函数和对数函数为例”[J].数学通报,2015,54(2):21-24.
[2]马复,王巧林.数学[M].南京:江苏教育出版社,2012.
编辑 赵瑞峰

