考虑变应力幅非线性累计损伤的高速铁路钢桁拱桥疲劳分析

张旭，蔺鹏臻

考虑变应力幅非线性累计损伤的高速铁路钢桁拱桥疲劳分析

张旭，蔺鹏臻

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

为分析钢结构桥梁在变应力幅循环条件下的疲劳寿命，基于非线性累计损伤方程，建立考虑变应力幅的疲劳损伤指标计算公式。以某高速铁路钢桁架拱桥为例，对比分析线性方法、等效应力幅法、递推法以及本文方法求解得到的疲劳寿命。研究结果表明：线性模型的计算结果偏小，等效应力幅法的计算误差随应力幅差值的增大而增大，递推法的计算精度高但运算量太大，本文提出的方法不仅能客观地反应疲劳损伤的过程，计算量小，而且计算结果与递推法的计算结果基本相同。对于钢桁架拱桥，竖腹杆的疲劳寿命最低，且同一根杆件的不同位置疲劳损伤相差往往很大，以竖腹杆为例，该类杆的下端、靠铁轨处的疲劳寿命最低，容易出现疲劳问题，在构造设计、施工质量方面应更加予以关注。

非线性损伤；疲劳寿命；变应力幅；钢桁拱桥

桥梁在长时间的连续反复荷载作用下，容易出现即使应力很低，构件也会突然发生脆性断裂这类疲劳破坏的现象[1]。由于实际桥梁中动载引起的应力循环大多数为变应力幅循环，为了预测疲劳寿命，人们提出了多种线性与非线性理论。目前工程中大都采用Miner线性理论分析结构的疲劳损伤，但该理论认为损伤与载荷的作用次序无关，所以不能客观地反映疲劳损伤的过程[2]。由此，国内外学者针对非线性损伤进行了大量研究：Lemaitre[3]基于连续介质热力学和耗散能理论，建立了非线性的高周疲劳损伤公式，WANG等[4−5]对公式中的系数做了系统的分析，并结合悬索桥梁加以运用，ZHAN等[6]通过考虑平均应力的影响，提出了从疲劳实验数据中获取材料参数的方法，LI等[7−8]提出了桥梁结构疲劳非线性累计损伤模型，蔡晓静等[9]通过实验找到平均应力对S-N曲线的影响关系，贾单锋等[10]通过高周疲劳实验找到Q345级钢的S-N曲线。目前，在利用Lemaitre方程求解非线性疲劳损伤时，无论用等效应力幅代替各个应力幅[5]，或用繁琐的递推公式[11]，均不能在变应力幅循环条件下准确方便地计算出疲劳损伤。本文在前人研究的基础上，通过分析应力循环块中每个应力幅对总疲劳寿命的影响，建立变应力幅循环条件下的疲劳损伤指标计算公式。结合实际算例发现：本文提出的方法计算精度高、计算量小，钢桁拱桥这类桥梁，竖腹杆的疲劳寿命最小、上弦杆最大，工程中应重点关注竖腹杆的构造设计与施工质量。

1 非线性累计疲劳损伤指标

1.1 疲劳损伤指标的定义

损伤力学中，以损伤指标来反映材料的劣化过程[12]。当损伤指标达到1时，结构发生破坏：

式中：为名义横截面积；为考虑损伤后的有效截面面积。

为便于理解，对单轴应力循环块中涉及的符号进行说明，见图1。

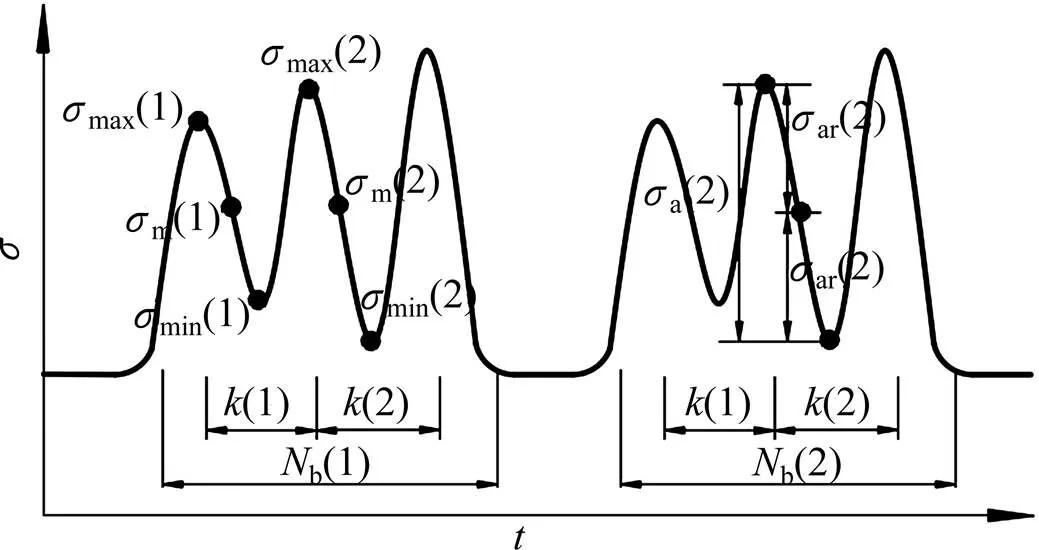
图1 单轴应力循环块中各符号示意图

图1中：m为平均应力；max和min分别为最大、最小应力；a为应力幅；ar为半应力幅；b为应力循环块的个数；为当前应力循环块中应力幅的数量。

1.2 高周疲劳演化方程

在单轴应力状态下，Lemaitre建立的高周疲劳演化方程[3]可简化为：

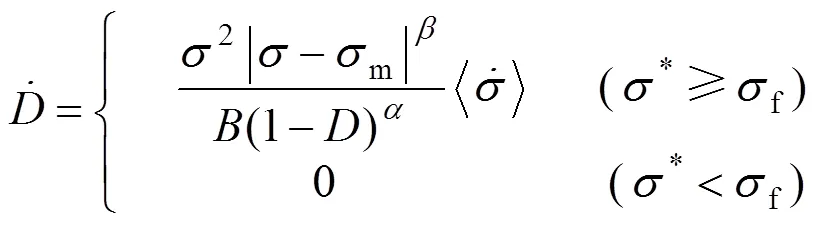
为便于分析，假定平均应力m等于0，且由于一个应力循环块中应力幅的数量较少，可认为疲劳损伤指标在一个应力循环块中没有变化。在一个应力循环块中对式(2)积分可得

式(3)求解：

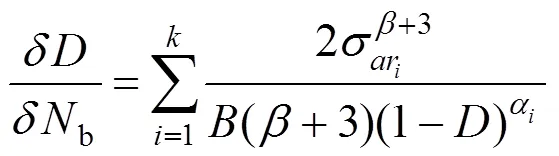
为考虑平均应力的影响，根据SWT方程[13]

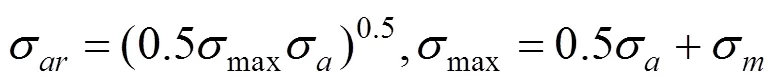
将式(5)回代到式(4)：

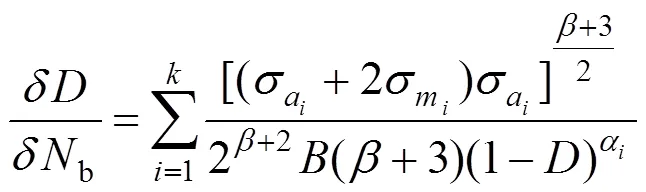
1.3 等效应力幅法

根据损伤等效原则[5]，得到等效应力幅

对式(6)进行积分，将式(7)代入，并取与等效应力幅Δef对应的系数e，得到考虑平均应力的疲劳损伤指标计算公式

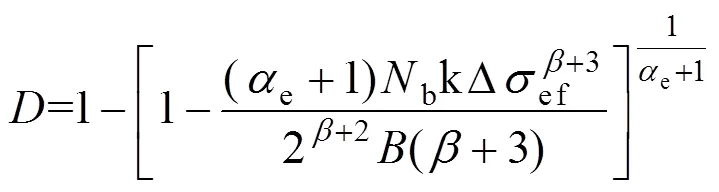
1.4 递推法

对式(4)等号右边的单个应力幅进行积分[11]，并结合式(5)，得到考虑平均应力时，全寿命周期中第个应力幅作用前后的疲劳损伤指标关系。

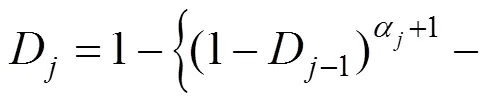
2 考虑变应力幅的疲劳损伤指标

2.1 各应力幅造成的疲劳损伤指标之间的比例关系

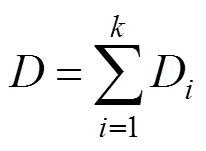
将式(11)代入式(4)：

令等号两边各个表达式分别相等：

2.2 总疲劳损伤指标

利用式(10)，将式(13)等号右边的疲劳寿命用表示：

为了表示方便，将式中的求和公式记为：

对式(14)积分：

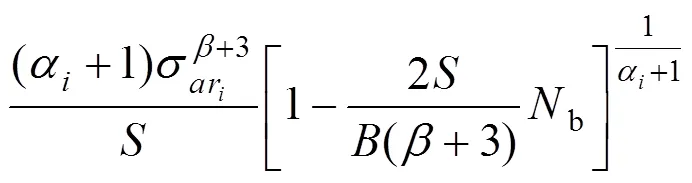
对求和，得到总疲劳损伤指标：

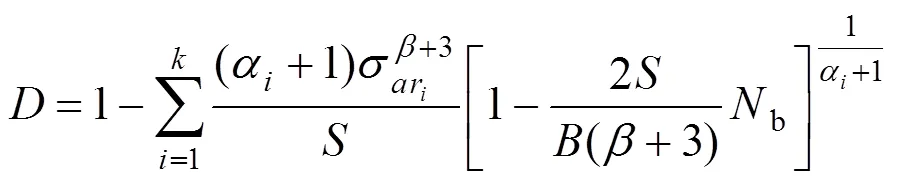
为了考虑平均应力的影响，且表示方便，记：

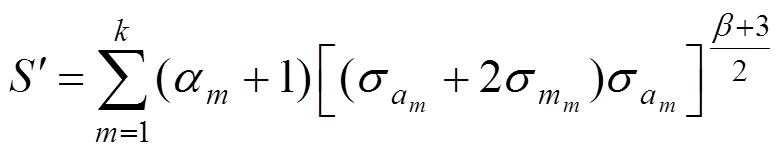
得到考虑平均应力的疲劳损伤指标：

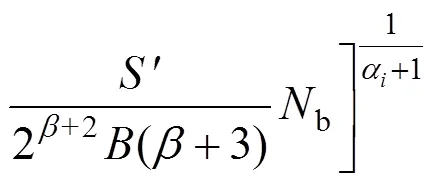
系数由公式=113−0.17×a确定[14]。分析英国钢结构疲劳设计规范[15]中螺栓连接(E连接类型)对应的S-N曲线[16]，得出系数=0，=4.868×1013。

3 系数α对非线性模型的影响

3.1 对比样本的设置

设置3个应力循环块作为对比分析样本。每个样本中设置2个应力幅，应力幅的差值分别设为40，70和100 MPa，且不考虑平均应力的影响，即m=0。各样本的应力幅a和等效应力幅Δef，见表1。

表1 对比分析样本

3.2 误差分析

因为递推法通过叠加每个应力幅造成的损伤进行计算，不存在系数取值不准确的问题，所以以递推法的计算结果为参照，分析其余2种非线性模型的误差。利用MATLAB软件，根据式(8)，(9)和(19)，计算得到3种非线性模型的疲劳损伤指标与应力循环次数的函数关系曲线见图2，误差率以及用时见表2。

表2 不同计算方法的误差率与用时

图2 累计疲劳损伤曲线

进一步分析应力循环块中应力幅的差值程度对等效应力幅法计算精度的影响，令应力循环块中含有2个应力幅，范围分别在0~500 MPa。在忽略平均应力的条件下，计算出疲劳寿命的误差率，见图3。

图3 等效应力幅法的误差率

分析结果表明：非线性计算模型可以客观地反应疲劳破坏的突发性，本文提出的方法的计算结果与递推法的计算结果近乎相同，误差率不超过1.0%，且计算量远小于递推法。等效应力幅法的计算误差随着应力幅差值的增大而增大，在应力幅为100 MPa的范围内，应力幅的差值引起的误差可达3.0%左右。

4 高速铁路钢桁拱桥疲劳分析

4.1 桥梁概况

以某3×168 m铁路连续钢桁架拱桥为例，如图4所示，分析该桥的疲劳寿命。该桥的主梁采用下承式钢桁梁结构，主桁采用有竖杆的三角形桁式，桁宽13.8 m和高12.8 m，上、下弦节间长度分别为11 m和12 m，采用正交异性钢桥面板和混凝土道碴槽板的桥面体系，吊杆为八角形截面，拱肋线形为二次抛物线，矢高28 m，矢跨比1/4.71，全桥材质为Q345qE钢材，支座均为球形钢支座。

单位：m

4.2 有限元模型

采用ANSYS15.0软件进行有限元建模。对于桁架桥，杆系结构能反应桥梁整体的力学行为，因此除桥面板采用板单元shell181模拟外，其余杆件均用3D梁单元beam189模拟，梁单元之间固结连接。全桥的有限元模型共计梁单元5 189个，板单元2 106个，见图5。图4中79 m处A、B节点的有限元模型以及截面的4个角点的位置编号见图6，单元局部坐标系为：轴为杆单元轴向方向，与轴为截面高宽方向。主要杆件的截面特性值见表3，括号里为支座附近杆件的特性值。

图5 有限元模型(半跨)

图6 桥梁A，B节点处的有限元模型

表3 各类杆件的截面几何特性

4.3 疲劳荷载

整体动力分析中的荷载主要包括：自重、二期恒载、列车荷载。钢材容重为76.98 kN/m3，二期恒载取175 kN/m。列车荷载采用高速铁路典型疲劳列车，编组模式为2节机车+8节客车[17]，双线同时加载，对向行驶，设计时速为250 km/h，轴重1取为140 kN，轴重2取为230 kN，轴重布置见图7。

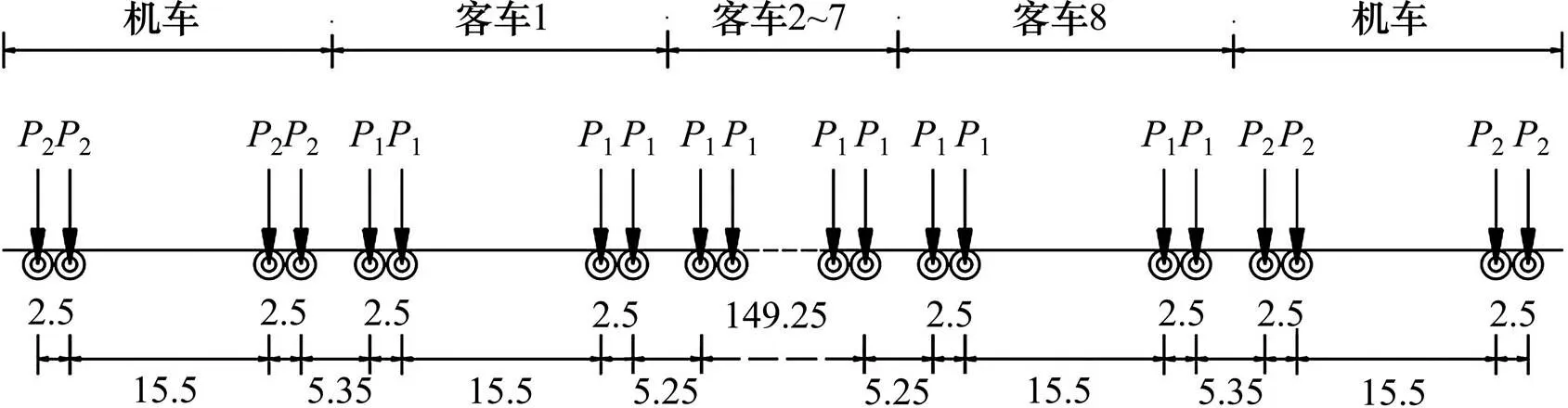
单位：m

列车荷载在模型上的实现采用当载荷移动过程中落在移动方向2相邻节点之间时，载荷按线性插值分配给前、后节点的方法[18]。

4.4 典型杆件疲劳应力分析

材料阻尼为0.005，运动方程采用直接积分法求解，计算得到各杆件的截面边缘处的轴向应力时程曲线后，发现该桥的竖腹杆、斜腹杆、下弦杆、吊杆及上弦杆为受拉杆件，易发生疲劳破坏[19]。

双线加载的条件下，当列车行驶1.402 s至97.4 m时，位于78 m(426 m)处的B节点下弦杆的拉应力为各杆件在加载全过程中的最大值，此时刻各杆件的轴向应力云图见图8，需重点分析B节点附近各杆件的应力幅情况。

经过计算得知，全部受拉杆件中节点B的竖腹杆的角点2处的轴向应力幅最大，其应力时程曲线见图9，经过雨流计数法[20]统计后得到的雨流矩阵图见图10。A，B节点各杆件的截面的各角点的轴向最大应力幅见表4，各杆件的最大应力幅见图11(左)。

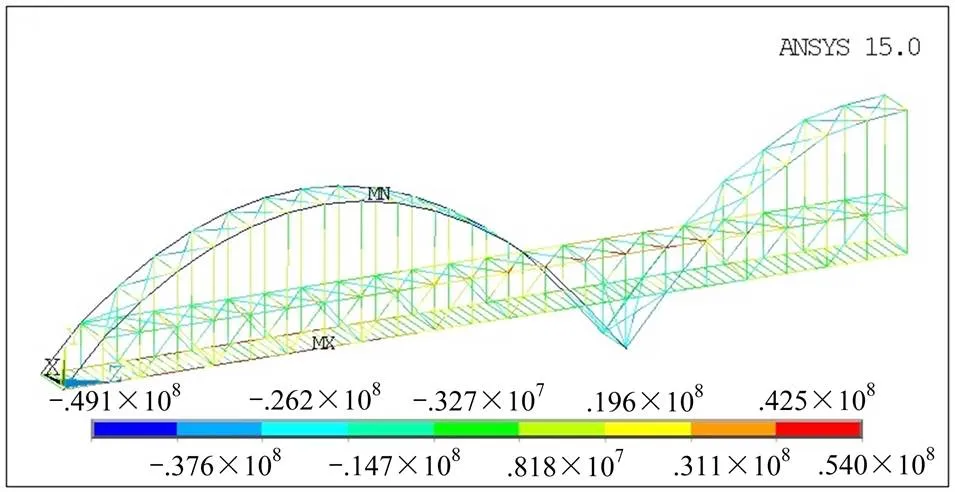
单位：Pa

图9 节点B竖腹杆的角点2的轴向应力时程曲线

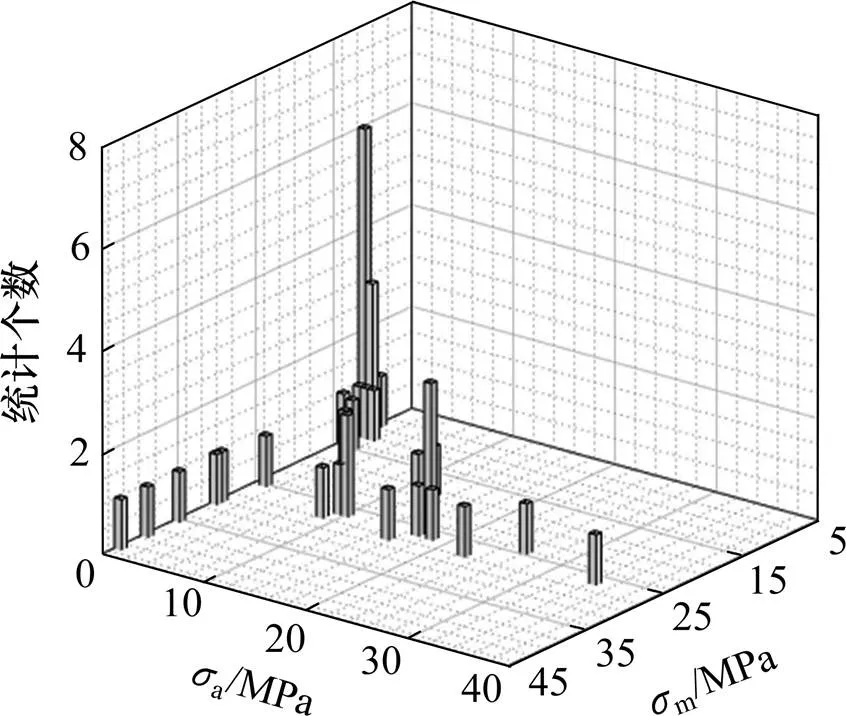
图10 节点B竖腹杆角点2的雨流矩阵图

应力分析结果表明：拉应力最大的杆件不一定应力幅最大，但应力幅最大的杆件会在其附近出现。同一根杆件的不同位置受动载影响的程度不同：竖腹杆、斜腹杆和吊杆下端的应力幅大于上端，上弦杆和下弦杆节点处大于节间处，竖腹杆、斜腹杆靠近铁路线的内侧大于外侧，下弦杆、上弦杆上边缘大于下边缘，吊杆远离铁路线的外侧大于 内侧。

表4 节点A，B处各杆件的最大轴向应力幅

4.5 分析疲劳寿命

分别用线性计算法[19]、等效应力幅法、递推法和本文方法计算各杆件的疲劳寿命。节点A，B处各杆件应力幅最大的角点处的疲劳寿命见表5。用递推法算得所有受拉杆件中应力幅最大的角点处的疲劳寿命见图11(右)。

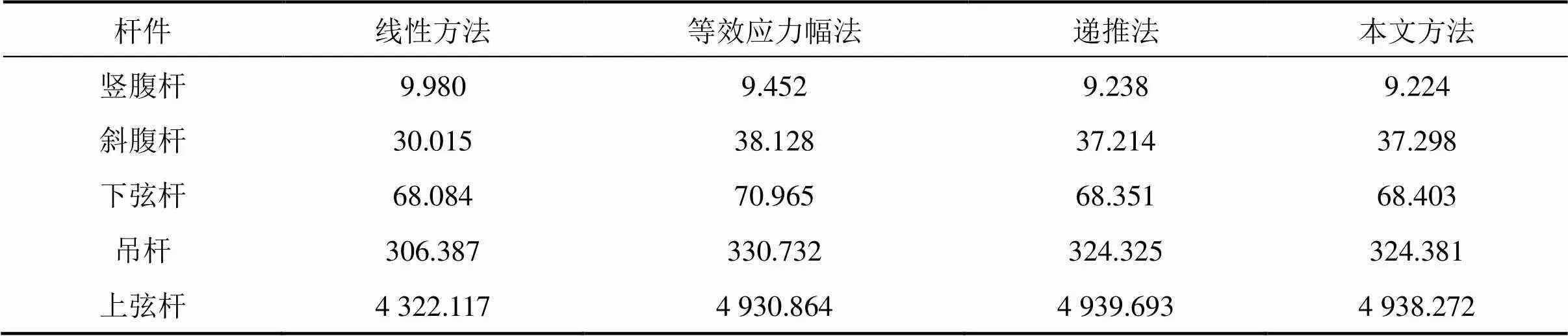
表5 节点B竖腹杆的疲劳寿命

本桥设计使用寿命100 a，参考运量大于3 000万吨/a的最不利情况，每天过桥的客车取270节，过桥的车次约为34次[17]，计算得到设计疲劳寿命为1.22×106次，而全桥的疲劳寿命由节点B处的竖腹杆决定，该处的计算疲劳寿命为9.238×106次，大于设计值，满足设计要求。

疲劳损伤计算结果表明：当应力幅的平均应力较大时，线性模型计算出的疲劳寿命偏大，当应力循环块中含多个大于应力疲劳极限的应力幅时，等效应力幅法的误差较大，本文方法的计算结果与递推法的计算结果几乎完全相同。应力幅和平均应力与疲劳寿命的关系为负相关，两者共同决定疲劳寿命，受拉杆件的疲劳寿命的大致规律由低到高为：竖腹杆＜斜腹杆＜下弦杆＜吊杆＜上弦杆。

图11 桥梁各杆件的最大应力幅(左)和疲劳寿命(右)

5 结论

2) 算例分析表明，本文推导的非线性累计损伤公式的计算结果与递推法的计算结果几乎完全相同，计算量与等效应力幅法的计算量基本相同，在实际工程中更加易于应用，而且与线性方法相比，本文方法能更客观地反应疲劳损伤过程。

3) 对于多跨钢桁架拱桥，跨中处受拉杆件的疲劳寿命由低到高为：竖腹杆<斜腹杆<下弦杆<吊杆<上弦杆，因此在工程设计中应适当增大竖腹杆的横截面积、优化连接方式，施工中注意提高施工质量，使这类杆件受动载引起的应力幅尽可能减小。

4) 疲劳寿命不仅与杆件类型有关，还与杆件的细部位置有关，以竖腹杆为例，该类杆的底端、靠轨道处的疲劳寿命最低，更易出现疲劳问题。

[1] 赵少杰, 任伟新. 超限超载交通对桥梁疲劳损伤及可靠度的影响[J]. 中南大学学报(自然科学版), 2017, 48(11): 3044−3050. ZHAO Shaojie, REN Weixin. Effect of overrun and overloaded vehicles on fatigue damage and reliability of highway bridges[J].Journal of Central South University (Science and Technology), 2017, 48(11): 3044−3050.

[2] 项海帆. 高等桥梁结构理论[M].2版. 北京: 人民交通出版社, 2013. XIANG Haifan. Advanced theory of bridge structures [M]. 2nd ed. Beijing: China Communications Press, 2013.

[3] Lemaitre J. A course on damage mechanics[M]. 2nd ed. Berlin: Springer-Verlag Berlin Heidelberg, 1996.

[4] WANG Huili, QIN Sifeng, WANG Yunjie. Nonlinear cumulative damage model and application to bridge fatigue life evaluation[J]. Advances in Structural Engineering, 2018, 21(9): 1402−1408.

[5] 王会利, 秦泗凤, 谭岩斌. 考虑非线性累计损伤的桥梁疲劳寿命分析[J]. 大连理工大学学报, 2016, 56(4): 362−366. WANG Huili, QIN Sifeng, TAN Yanbin. Fatigue life analysis of bridges considering nonlinear cumulative damage[J]. Journal of Dalian University of Technology, 2016, 56(4): 362−366.

[6] ZHAN Zhixin, HU Weiping, ZHANG Miaomeng. Revised damage evolution equation for high cycle fatigue life prediction of aluminum alloy LC4 under uniaxial loading[J]. Applied Mathematics & Mechanics, 2015, 36(9): 1185−1196.

[7] LI Z X, CHAN T H T, KO J M. Fatigue analysis and life prediction of bridges with structural health monitoring data — Part I: methodology and strategy[J]. International Journal of Fatigue, 2001, 23(1): 45−53.

[8] CHAN T H T, LI Z X, KO J M. Fatigue analysis and life prediction of bridges with structural health monitoring data—Part II: application[J]. International Journal of Fatigue, 2001, 23(1): 55−64.

[9] 蔡晓静, 许金泉. 各种平均应力下高周疲劳极限间的定量关系[J]. 工程力学, 2015, 32(10): 25−30. CAI Xiaojing, XU Jinquan. A quantitative relationship of high cycle fatigue limit with mean stresses[J]. Engineering Mechanics, 2015, 32(10): 25−30.

[10] 贾单锋, 廖小伟, 崔佳. Q345qD桥梁钢高周疲劳性能及-P-S-N曲线试验研究[J]. 天津大学学报, 2016, 49(4): 122−128. JIA Danfeng, LIAO Xiaowei, CUI Jia. Experimental study on high cycle fatigue behavior and-P-S-N curves of bridge steel Q345qD[J]. Journal of Tianjin University (Science and Technology), 2016, 49(4): 122−128.

[11] 陈志为, 徐幼麟. 考虑非线性累计损伤的大跨多荷载桥梁的疲劳可靠度评估[J]. 西南交通大学学报, 2014, 49(2): 213−219. CHEN Zhiwei, XU Youlin. Fatigue reliability analysis of multi-loading suspension bridges considering nonlinear accumulative damage[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 213−219.

[12] 张彦军, 张淼. 基于损伤力学方法的带板连接件疲劳寿命预估[J]. 机械强度, 2011, 33(3): 443−449. ZHANG Yanjun, ZHANG Miao. Fatigue life prediction of the joint plate based on damage mechanics method[J]. Journal of Mechanical Strength, 2011, 33(3): 443−449.

[13] Dowling N E. Mean stress effects in strain-life fatigue[J]. Fatigue & Fracture of Engineering Materials & Structures, 2009, 32(12): 1004−1019.

[14] LI Z X, CHAN T H T, KO J M. Fatigue damage model for bridges with under traffic loading: application made to Tsing Ma Bridge[J]. Theoretical and Applied Fracture Mechanics, 2001, 35(1):81−91.

[15] BS 7608—1993, Fatigue design and assessment of steel structures British standard[S].

[16] CHEN Z W, XU Y L, XIA Y. Fatigue analysis of long-span suspension bridges under multiple loading case study[J]. Engineering Structures, 2011, 33(12): 3246− 3256.

[17] 杨鑫炎. 高速铁路钢桥疲劳评估标准车型研究[J]. 城市道桥与防洪, 2014, 28(7): 331−333. YANG Xinyan. Research on fatigue evaluation standard model of high speed railway steel bridge[J]. Urban Roads Bridges & Flood Control, 2014, 28(7): 331−333.

[18] 朱世峰, 马明, 周志祥. 计算结构动力响应中移动载荷的简化方法[J]. 四川建筑, 2008, 28(2): 139−141. ZHU Shifeng, MA Ming, ZHOU Zhixiang. A simplified method for calculating the moving load in structural dynamic response[J]. Sichuan Architecture, 2008, 28(2): 139−141.

[19] GB 50017—2017, 钢结构设计标准[S]. GB 50017—2017, Standard for design of steel structures [S].

[20] 毕继红, 陈花丽, 任洪鹏. 基于雨流计数法的接触线疲劳寿命分析[J]. 铁道学报, 2012, 34(6): 34−39. BI Jihong, CHEN Huali, REN Hongpeng. Analysis on fatigue life of contact wire based on rain-flow counting method[J]. Journal of the China Railway Society, 2012, 34(6): 34−39.

Fatigue analysis of high-speed railway steel trussed arch bridge considering nonlinear cumulative damage of variable stress range

ZHANG Xu, LIN Pengzhen

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to analyze the fatigue life of steel bridge under variable stress range cycle, based on the nonlinear cumulative damage equation, the fatigue damage index considering variable stress range was established. Taking a high-speed railway simply supported steel truss bridge as an example, the effects of Linear Method, Equivalent Stress Range Method, Recursive Method and the method of this paper on fatigue life calculation results were compared and analyzed. The results show that the calculation result of the Linear Model smaller than other method, and the error of the calculation results of the Equivalent Stress Range Method increases with the increase of the stress range difference. The accuracy of the Recursive Method is high but the calculation amount is too large. The method proposed in this paper can objectively reflect the process of fatigue damage, and its calculation results are basically the same as those of the Recursive Method. For steel trussed arch bridges, the fatigue damage at different positions of the same rod is often very different. Taking the vertical web as an example, the fatigue life is the lowest near the rail and the bottom of the rod, which is relatively prone to fatigue problems. More attention should be paid to the structural design and construction quality of such rods.

nonlinear damage; fatigue life; variable stress range; steel trussed arch bridges

U24

A

1672 − 7029(2020)03 − 0540 − 09

10.19713/j.cnki.43−1423/u.T20190561

2019−06−23

国家自然科学基金重大项目(11790281)；国家自然科学基金资助项目(51878323)；中国铁路总公司科技研究开发计划课题(2017G010-C)

蔺鹏臻(1977−)，男，甘肃甘谷人，教授，博士，从事桥梁结构设计理论的研究；E−mail：pzhlin@mail.lzjtu.cn

(编辑 涂鹏)