人民币汇率与股价之间的传导机制——基于DCC-GARCH 模型的实证检验

（武汉大学经济与管理学院， 武汉 430072）

引言

2008 年由美国房地产市场引发的次贷危机给全球金融市场造成了严重冲击，全球主要证券市场的股价指数纷纷出现了暴跌。这次危机期间传统货币政策的无效性让世界各国意识到，仅凭传统的财政政策和货币政策是无法实现金融稳定的。2009 年，国际清算银行提出用宏观审慎的概念来解决危机中“大而不能倒”、顺周期性和监管不足等问题。2010 年，中国明确提出要“构建逆周期的金融宏观审慎管理制度框架”。不管是微观审慎还是宏观审慎，目标都是要实现金融稳定，而金融稳定的重点是汇率和金融资产价格的稳定［1］。

外汇市场是连接国内资本市场和国外资本市场的重要桥梁，汇率作为开放经济的关键经济变量之一，对国民经济有着重要的影响。从宏观上看，汇率的变动会影响国际资本的流向；从微观上看，汇率的波动会通过影响产品的生产成本和相对价格等方式对企业的生产经营活动带来显著的影响。随着我国汇率市场化进程的推进，以及美元加息和贸易摩擦加剧等因素的影响，人民币汇率的波幅会不断增加。

股票市场是在中国经济转型过程中逐渐发展起来的新兴市场。我国采取了多项改革措施来帮助国内股票市场与国际接轨，如2005 年4 月启动股权分置改革，2014 年11 月17 日开通沪港通，2016 年12 月5 日启动深港通以及2018 年12 月14 日开通沪伦通等。随着经济的不断发展，我国经济总量跃居世界第二，2018 年我国GDP 首次突破90 万亿，居民可支配收入不断增加，可是投资渠道却相对有限，股票市场作为我国金融市场的重要组成部分，是我国居民的主要投资渠道。

张碧琼和李越（2002）利用我国数据发现汇率和股价之间存在着某种传导机制，二者相互影响，表现出明显的相关性［2］。因此，在汇率市场化改革的进程中需要控制汇率变动对国内股票市场的冲击，避免外部经济冲击通过人民币汇率使实体经济产生大幅波动。鉴于此，在我国经济进入新常态的背景下，本文研究2008 年金融危机以来人民币汇率和股价之间的传导机制，这对维护我国金融体系稳定以及防范系统性金融风险的发生具有重要意义。

研究汇率和股价之间传导机制的最经典的两个理论是流量导向模型（Flow-oriented Model）和存量导向模型（Stock-oriented Model）。流量导向模型是Dornbusch 和Fisher 在1980 年提出的，该理论认为一国汇率的变动会通过影响商品的国际竞争力来影响该国的经常账户，进而影响该国进出口企业的利润和未来现金流，最终导致股价发生变化［3］。存量导向模型是Branson（1981）和Frankel（1983）提出来的，该理论认为一国股价的变动会影响国际投资者对它的投资，从而通过影响对该国货币的需求使利率发生变化，进而影响汇率［4，5］。

在实施跨境贸易人民币结算、与多个国家签署双边本币互换、建立离岸人民币市场、提出“一带一路”倡议以及成立亚投行等举措的帮助下，人民币国际化进程取得了很大的进展。与汇率市场化的进程相比，我国资本账户开放的步伐相对较慢。资本项目尚未完全开放，资本账户还存在着较多的管制，我国股市对外资的进入设置了诸多限制。因此，从理论上推断，相较于从股价到汇率的传导机制，在我国从汇率到股价的传导机制会更通畅，即我国汇率和股价之间的关系应该符合流量导向模型。

为了判断这一推断是否正确，本文采用动态相关系数-广义自回归条件异方差（DCC-GARCH）模型和VAR 模型，利用我国人民币汇率数据和股价数据实证检验汇率和股价之间的传导机制，判断二者之间的关系究竟符合哪一种理论模型，并分析了相应的影响机制。这不仅丰富了相关方面的研究，有助于我国股票市场的健康长远发展，而且能够为监管当局进行系统风险控制和制定相关政策提供一定的理论支持。

1 文献综述

1973 年布雷顿森林体系解体之后，流向导向模型和存量导向模型这两个经典理论相继被提出，国内外越来越多学者围绕着这两个理论进行实证检验。

早期的研究对象主要集中在发达国家，尤其是美国，如Aggarwal（1981）、Soenen 和Henniger（1988）和Ajayi 和Mougoue（1996）等［6-8］。而在1997 年亚洲金融危机之后，学者们开始把目光转向新兴市场国家。Abdalla 和Murinde（1997）以巴基斯坦、菲律宾、韩国和印度4 个国家为研究对象［9］。Aydemir 和Demirham（2009）、Rjoub（2012）和Doong（2005）等也对该问题进行了研究［10-12］。

还有不少学者同时研究发达国家和新兴市场国家，Pan 等（2007）选择了7 个亚洲新兴市场国家和地区作为研究对象，研究发现股价和汇率之间的传导机制依赖于汇率制度、股票市场规模和资本控制程度等因素［13］。Moore 和Wang（2014）选择了6 个亚洲新兴市场国家和4 个发达国家，实证结果表明汇率和股价之间的传导机制取决于这些国家金融市场的成熟度［14］。Wong（2017）采用CCC、DCC 和MGARCH 等多种回归方法，以德国、菲律宾、马来西亚和韩国等多个国家为样本进行了相关研究［15］。

与国外学者相比，我国学者在这方面的研究起步较晚。邓燊和杨朝军（2008）研究了2005 年7 月21 日人民币汇率制度改革以后我国汇率和股价之间的关系，发现汇率制度改革以来，人民币升值是股市上涨的单向Granger 原因［16］。张兵等（2008）研究表明在短期内汇率和股价之间存在着交互影响，在长期内人民币汇率和股价之间的关系符合流量导向模型［17］。刘维奇和董晨昱（2008）以及刘莉和万解秋（2011）通过实证研究发现汇率和股价之间的关系是随时间变化的［18，19］。

上述这些文献都是用汇率和股价这两个变量建立实证模型来判断汇率和股价之间的相关关系以及传导机制，还有一些学者则引入了其他变量来考虑汇率和股价之间的关系。吴丽华和傅广敏（2014）用TVP-SV-VAR 模型分析人民币汇率、短期资本和股价三者之间的动态关系［20］。陈创练等（2017）用TVP-VAR 模型研究了我国外汇市场、债券市场和股票市场之间的动态关系［21］。陶士贵和范佳奕（2018）用TVP-SV-VAR 模型发现QFII、人民币汇率和股价三者之间的关系是随时间变化而变化的［22］。然而，还有一些学者的研究表明汇率和股价之间不存在长期均衡关系，如巴曙松和严敏（2009），王兆瑞和方壮志（2016）等［23，24］。

通过上述文献梳理可以发现，国内外文献从多种角度分析了不同时期内各个国家汇率和股价之间的关系。相较于国外学者而言，国内学者在这方面的研究起步较晚，所采用的计量方法主要是Granger 因果检验、协整检验和VAR 系列模型，根据汇率和股价的脉冲响应图来判断汇率和股价之间的传导机制。本文与国内现有文献的主要不同之处在于：（1）用DCC-GARCH 模型计算汇率和股价之间的动态条件相关系数（DCC），动态条件相关系数不仅可以很好地代表汇率和股价之间的相互依赖程度，而且，时变的动态条件相关系数还可以反映出经济状况的改变；（2）分别选择净出口和中美利差作为经常账户和资本账户的代理变量，根据净出口和利差对DCC 的解释程度来判断汇率和股价之间的传导机制，当净出口对DCC 的影响显著时，汇率和股价的关系符合流向导向模型，当利差对DCC 的影响显著时，汇率和股价的关系符合存量导向模型。

2 实证部分

本文以DCC-GARCH 模型为基础，先计算出汇率收益率序列和股价收益率序列之间的动态相关系数，然后在此基础上用VAR 模型分析人民币汇率和股价之间的传导机制。

2.1 DCC-GARCH 模型简介

Engle（2002）提出了动态条件相关系数-自回归条件异方差模型（DCC-GARCH 模型），该模型假定变量间的相关系数是随时间变化而变化的，每一期的相关系数都依赖于前期所能得到的所有信息，该模型可以很好地刻画变量间的联动性。模型假设收益率序列的残差项服从均值为0、协方差矩阵为Ht的正态分布。DCC-GARCH（1，1）模型的具体方程如下：

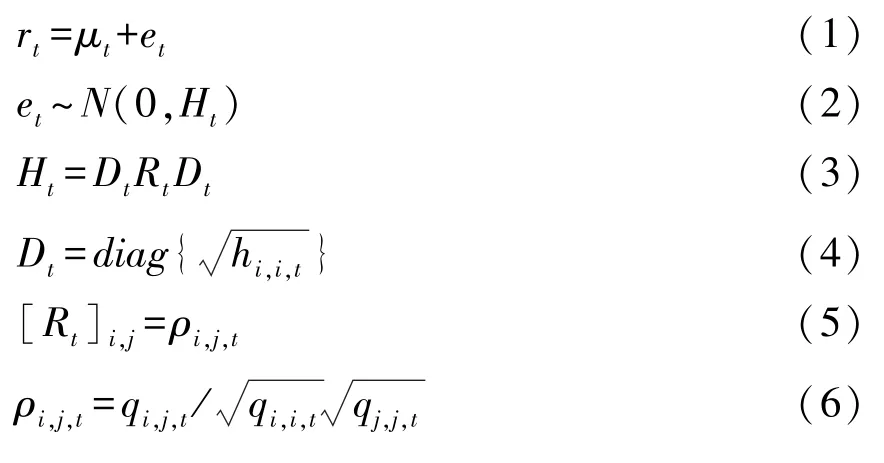
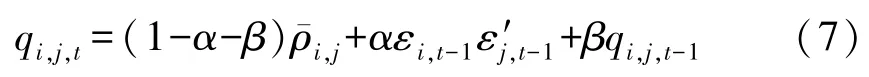
其中Dt是单变量GARCH 模型计算出的条件标准差所组成的对角矩阵，Rt就是所要求的动态条件相关系数矩阵。ρi，j，t是变量i和变量j在时刻t的动态相关系数，是标准化残差的无条件方差，εi，t是变量i的标准化残差序列，是变量j的标准化残差序列，α是滞后一期的标准化残差的系数，β是滞后一期的条件协方差的系数。将式（7）写成矩阵形式，如下所示：

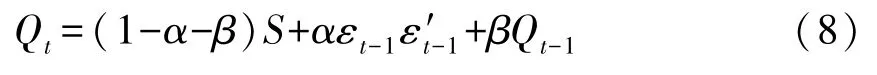
Qt是标准化残差序列的条件协方差矩阵，S为标准化残差的无条件方差矩阵，εt和是向量标准化残差，α和β是系数矩阵。

DCC-GARCH 模型的计算分为两步：（1）针对每个变量建立单变量GARCH 模型，用残差除以条件方差，得到标准化残差序列；（2）用第一步得到的标准化残差序列计算动态条件相关系数。

2.2 变量选择与数据来源

由于我国在相当长的时间内采取了盯住美元的汇率政策，因此本文选择美元兑人民币在岸汇率（EX）作为汇率的代理变量。股价指数选择的是上证综指（SP），它的样本股包括所有在上海证券交易所挂牌上市的股票，是我国最早发布的指数，具有很好的代表性而且被广泛使用。基于数据的可得性以及避免2008 年国际金融危机的影响，本文的数据区间是2009 年6 月1 日至2018年10 月31 日，扣除节假日等没有交易数据的天数外，还有2291 个数据，数据来源是WIND 数据库。本文所使用的计量软件是Stata15.0，各变量的描述性统计结果见表1。

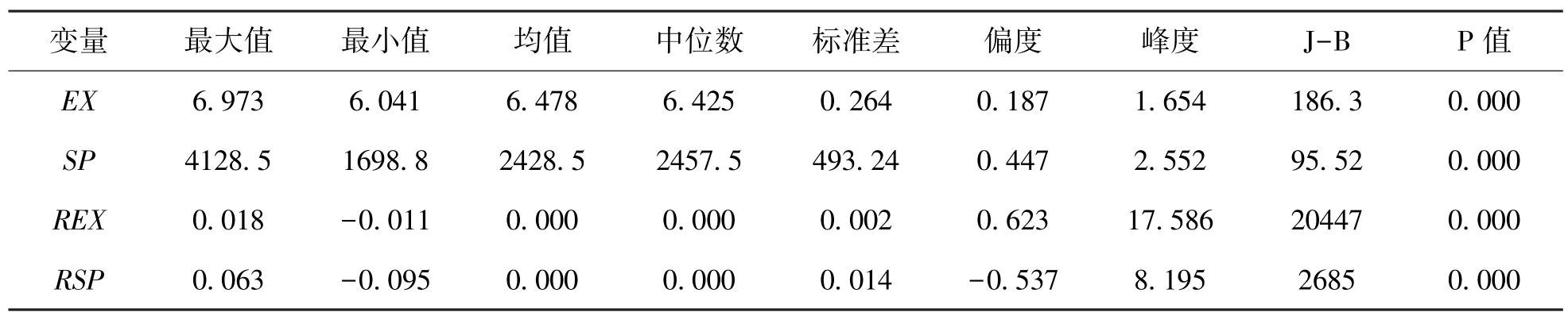
表1 描述性统计结果

由表1 中的J-B 统计量和p 值可知，变量均不服从正态分布，从偏度和峰度可以看出，收益率序列均存在明显的尖峰厚尾，这是金融时间序列的普遍特征，适合建立GARCH 类模型。

3 动态相关系数估计

3.1 ARCH 效应检验

建立任何计量模型的前提条件是变量必须是平稳的时间序列，为了获得平稳的时间序列，取各原始序列的对数收益率序列，计算方法如下：

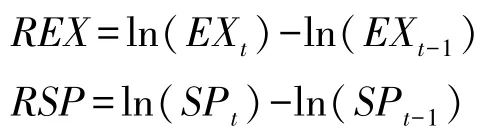
变量的原序列及其收益率序列的ADF 检验结果表略。由ADF 检验结果可知，在1%的显著性水平上，两个变量的原序列都不符合平稳性要求，而它们的收益率序列都是平稳的时间序列，可以用来建立GARCH 模型。建立GARCH 模型的前提条件是时间序列存在ARCH 效应，因此需要对变量的收益率序列进行ARCH 效应检验，本文采用最常用的LM 检验（结果表略），从LM 检验结果可以看出，在不同的滞后阶数下，P 值都为0，这表明汇率和股价指数的收益率序列均存在非常明显的ARCH 效应。综上，可以建立GARCH 模型。

3.2 单变量GARCH 模型的参数检验

Bollerslev 等（1992）表明，最简单的GARCH（1，1）模型就可以很好地拟合金融时间序列的波动特征［25］。因此本文选择GARCH（1，1）模型来估计单变量GARCH 模型，针对每个变量单独建立的GARCH（1，1）模型的回归结果表略。

ARCH 参数是滞后的残差平方项的系数，GARCH 参数是滞后的条件方差项的系数，这两项参数之和反映收益率序列波动持久性程度。由GARCH 回归结果可以看出，汇率收益率序列和股价收益率序列的ARCH 系数和GARCH 系数之和均非常接近于1，这表明收益率序列目前的波动趋势还会在相当长的时间内持续下去。

3.3 DCC-GARCH（1，1）模型估计结果

DCC-GARCH（1，1）模型的估计结果表略。由DCC-GARCH（1，1）回归结果可知，Lambda1 ＋Lambda2 之和非常接近于1，这表明模型不仅是整体平稳的，而且汇率收益率序列与股价指数收益率序列之间的动态相关性非常显著，检验结果有效。DCC-GARCH（1，1）模型的动态相关系数回归结果见表2 和图1。

表2 动态相关系数回归结果

从表2 可以看出，动态相关系数均值为-0.095，说明从总体来看人民币汇率收益率和股价指数收益率的相关性处于较低水平，且为负值，不过波动性较大，最大时达到了0.076，最小时低于-0.3。

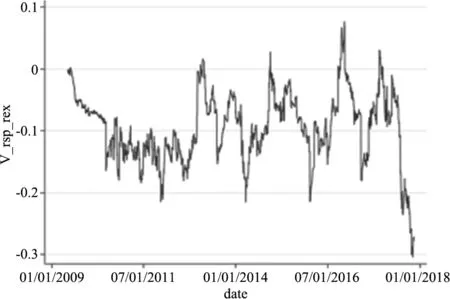
图1 人民币汇率和股价指数的动态相关系数

从图1 进一步看出，人民币汇率收益率序列和股价指数收益率序列的动态相关系数基本一直为负，这与Moore 和Wang（2014）［14］利用6 个新兴市场国家和4 个发达国家数据所得到的实证结果是一致的。意味着人民币汇率收益率和股价收益率之间的变动是反向的，当人民币汇率收益率上升时，股价指数收益率就会下降。而且动态相关系数的波动比较频繁剧烈，波动范围主要集中在-0.2～0 之内，不过从2018 年开始，动态相关系数一直在下降，这表明汇率收益率和股价收益率序列之间的负向联动更加显著了。

4 传导机制的分析

VAR 模型重点关注变量之间的跨期相关性，注重因果关系的分析，很适合本文的研究目的。因此，为了判断人民币汇率和股价之间的传导机制，用上一步得到的DCC 序列、利率数据和净出口数据建立VAR 模型，选取金融发展程度作为控制变量，数据频率均为月度，样本区间是2009 年6 月至2018 年10 月。

DCC：动态相关系数。对上一步得到的DCC序列进行ADF 检验，结果显示在1%的显著性水平上，序列是平稳的。因为其他宏观经济变量只能得到月度数据，而相关系数加总后会失去原本的经济含义，因此本文直接选择每个月最后一个交易日的DCC 数据。

r-r*：中国和美国的利差。参照Moore 和Wang（2014）［14］的做法，选择利差作为存量导向模型的代理变量。如果利差对DCC 序列的影响显著，那么汇率和股价的关系符合存量导向模型。其中r是国内的利率数据，选择最具有代表性的中国银行间同业拆借利率的月度数据，数据来源是中经网数据库，r*是美国联邦基金利率，数据来源是美联储。

CAS／GDP：净出口。同样参照Moore 和Wang（2014）［14］的做法，选择净出口数据作为流量导向模型的代理变量。如果净出口对DCC 序列的影响显著，那么汇率和股价之间的关系符合流量导向模型。其中CAS 是国内的净出口数据，单位是亿美元，数据来源是中经网。GDP 是上一年度的国内生产总值数据，单位是亿元，数据来源是WIND数据库。从中国统计年鉴获得人民币兑美元的年平均汇率，将GDP 的单位从人民币转化为美元后进行计算。

FD／GDP：金融发展程度。借鉴国内外学者的普遍做法，选择股票市场市值、广义货币供应量和金融机构贷款余额数据之和与上一年度的GDP 数据之比作为金融发展程度的代理变量。数据来源是WIND 数据库。

接下来进入具体的VAR 模型建模阶段，首先需要对各个变量进行单位根检验，判断变量是否是平稳的时间序列。

4.1 单位根检验

分别对这4 个变量进行ADF 检验，结果如表3所示。从表3 可以看出，DCC、r-r*和CAS／GDP都在5%的显著性水平上拒绝了原假设，因此这3个变量序列都是平稳的，不存在单位根。控制变量FD／GDP的原序列在5%的显著性水平上无法拒绝原假设，但是其一阶差分序列是平稳的，而且它是作为控制变量，并不需要从经济学的意义上解释它。因此，选择DCC、r-r*和CAS／GDP的原序列以及FD／GDP的一阶差分序列来建立VAR模型。

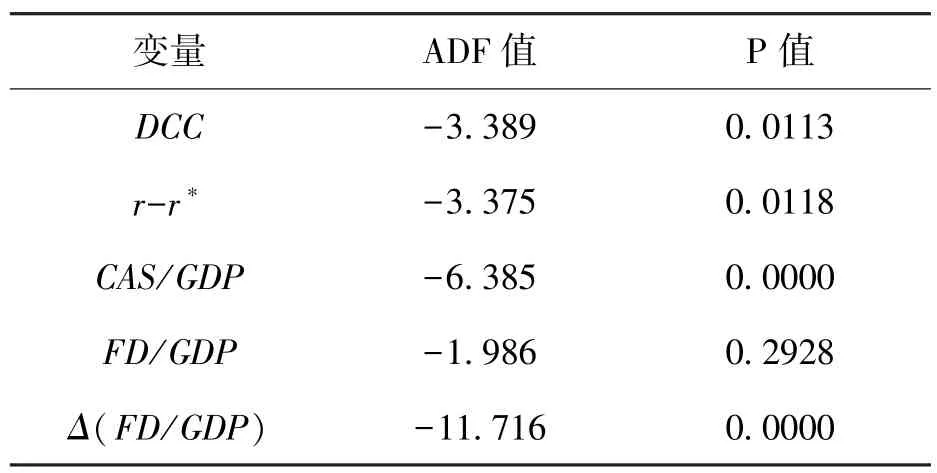
表3 ADF 检验结果

4.2 滞后阶数的选择

从表4 可以看出，在FPE 准则、AIC 准则、HQIC 准则和SBIC 准则下最优的滞后阶数是一阶，而根据LR 值应该选择滞后三阶的模型。当不考虑滞后一阶的模型时，滞后三阶的模型的AIC 值是最优的。而且宏观经济变量的变化对实体经济发挥作用存在一个显著的时滞，因此选择滞后三阶的模型更符合实际。

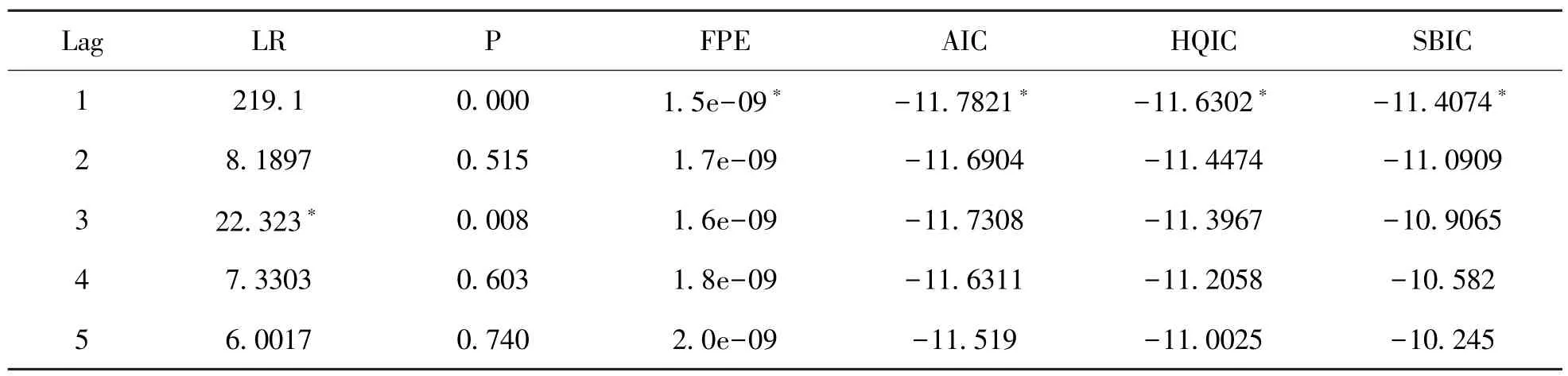
表4 滞后阶数的选择

4.3 VAR（3）模型的实证结果

用DCC、r-r*、CAS／GDP和DCC 建立VAR（3）模型，同时选择Δ（FD／GDP）作为控制变量，结果如表5 所示。

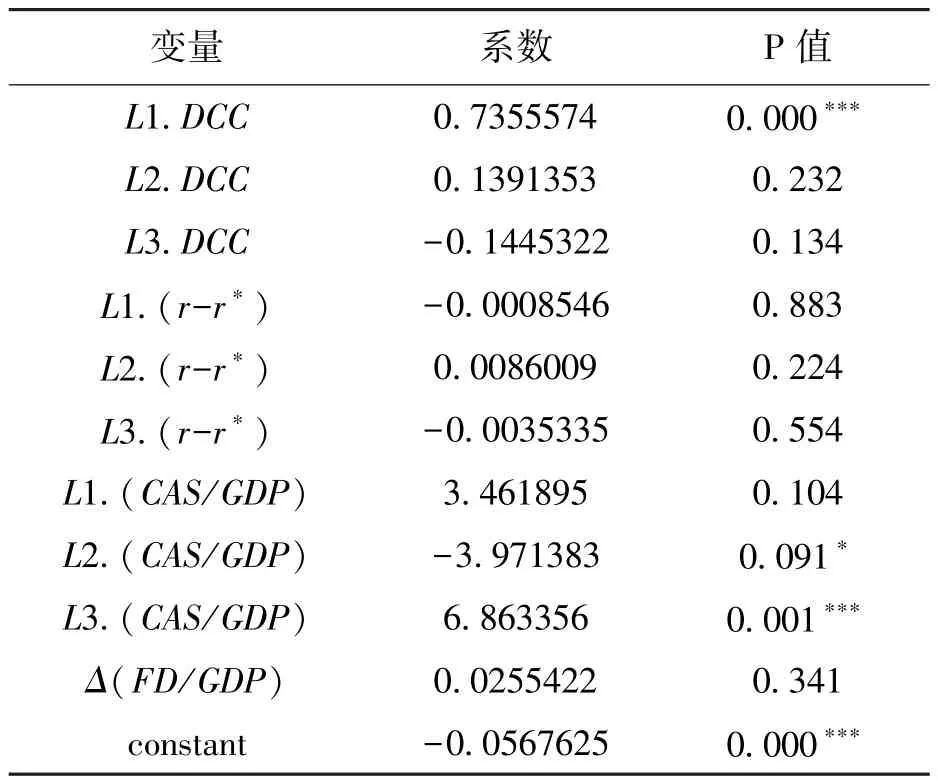
表5 VAR（3）模型实证结果

考虑到时滞的存在，主要看滞后三阶变量的系数。从表5 可以看出中国和美国的利差（r-r*）对DCC 的影响为负，但是并不显著；同时，净出口（CAS／GDP）对DCC 的影响为正，而且很显著。接下来分析动态相关系数对净出口冲击和利差冲击的脉冲响应图。

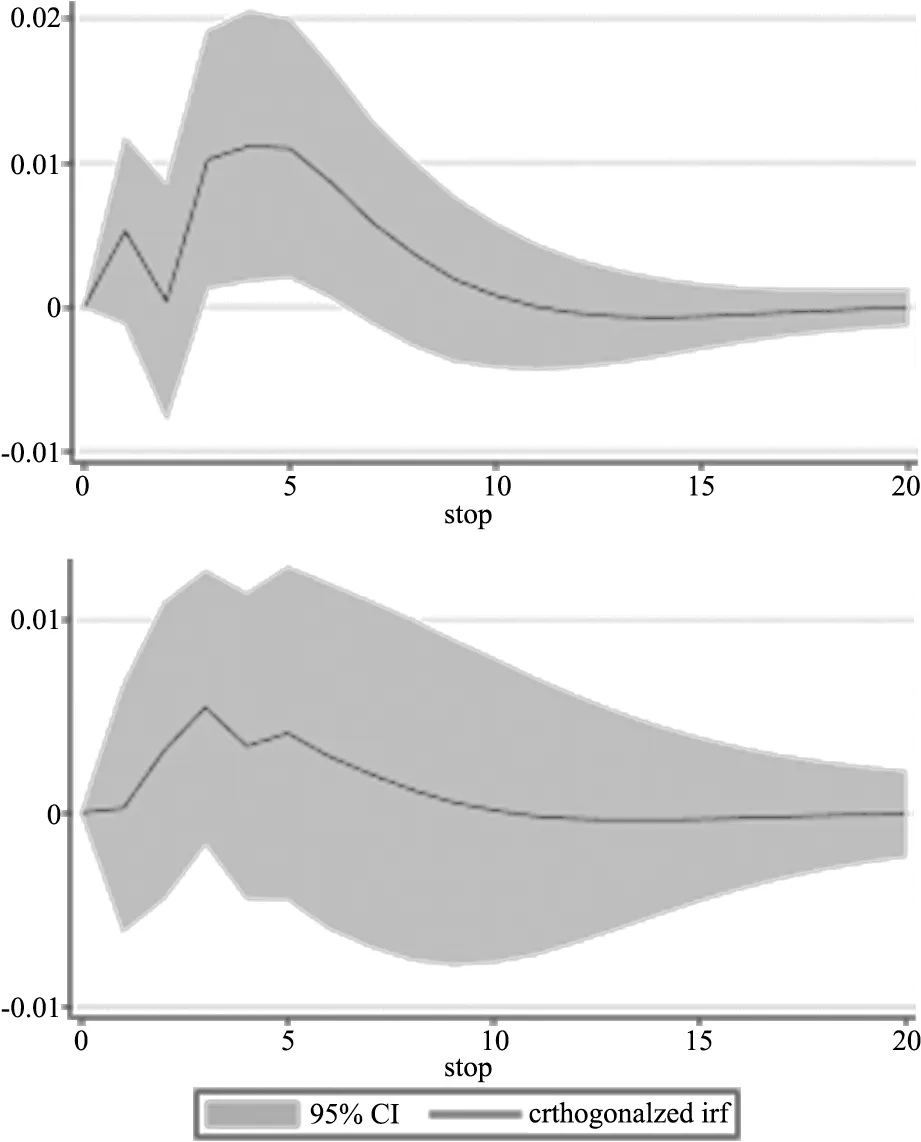
图2 动态相关系数对CAS／GDP 冲击和r-r*冲击的脉冲响应图

从上面两个脉冲响应图可以很明显地看出，净出口和利差的正向冲击在短期内都会对动态相关系数产生正向影响，长期内影响趋近于0，其中净出口的冲击对动态相关系数的影响更显著。因此，结合表5 的实证结果可以判断，在我国汇率和股价之间是通过经常账户作为中间变量来传导的，符合流量导向模型。这一结论与我国的实际情况相符，相较于汇率市场化的进程而言，我国资本账户开放的进展较慢，尤其是证券投资这个部分。其中，随着银行间债券市场开放力度的增大，债券类项目的开放程度比较高，但股票类证券还存在着包括投资额度在内的诸多限制。因此，从股价到汇率的传导渠道并不通畅。当人民币汇率上升时（本文采用的是直接标价法，汇率上升意味着人民币贬值），我国出口商品在国际市场上的竞争力上升，出口金额增加，出口企业的利润增加，预期未来现金流也会增加，出口企业的股价也会随之上涨；与此同时，进口商品的价格增加，我国就会减少进口，由于成本增加，进口企业的利润会下降，预期未来现金流减少，进口企业的股价下降。但是我国是一个出口主导的市场，最终整个市场的股价还是会上升，而且在这个过程中经常账户盈余也会增加。

由于DCC 是汇率收益率序列和股价收益率序列之间的动态相关系数，可以将它理解为股价和汇率之间的二阶导系数，结合DCC 的符号为负可知，随着汇率上升的幅度越来越高，每一单位汇率的变动对股价产生的影响是递减的。进一步来说，净出口（CAS／GDP）对DCC 的影响为正，即随着净出口规模的增加，DCC 也会随之变大，因为DCC 本身是负数，所以随着净出口规模的增加，DCC 的绝对值越来越小，股价对汇率的一阶导系数变小得越来越慢，汇率对股价的影响更大更持久。这一点也符合一般的理论规律，随着净出口规模的不断增加，我国经济开放程度越来越高，汇率和股价之间的传导机制越来越通畅，汇率对股价的影响就会越来越显著。

5 稳健性检验

5.1 用月初的DCC 数据建立VAR 模型

前文用的是月末的DCC 数据建立VAR 模型，为了判断数据选取的时间对实证结论有无影响，选择月初的DCC 数据来进行稳健性检验。根据信息准则判断应该建立VAR（4）模型，具体的实证结果如表6 所示。

表6 VAR（4）模型实证结果

考虑到时滞的存在，主要看滞后四阶的系数。可以发现结论与前面得到的结论是类似的。中国和美国的利差（r-r*）对DCC 的影响为负，并不显著；同时，净出口（CAS／GDP）对DCC 的影响为正，而且很显著。

5.2 改变金融发展程度的计算方法

为了判断不同代理变量的选取对实证结论有无影响，改变金融发展程度的计算方法来进行稳定性检验，将金融机构贷款余额换成发放给私人部门的贷款，数据来源是WIND 数据库。根据信息准则判断应该建立VAR（3）模型，具体的实证结果如表7 所示。

考虑到时滞的存在，主要看滞后三阶的系数。可以发现得到的结论与前面类似。中国和美国的利差（r-r*）对DCC 的影响为负，并不显著；但是净出口（CAS／GDP）对DCC 的影响为正，而且很显著。

5.3 自回归分布滞后模型（ARDL）

VAR 模型注重变量间的跨期因果关系分析，为了判断模型的选择对实证结论有无影响，考虑到时滞的存在，将前文中的VAR 模型换成更侧重于考虑时滞的自回归分布滞后（ARDL）模型来进行稳健性检验。利用Eviews10 基于AIC 准则来筛选滞后阶数，筛选出的模型是ARDL（1，0，3，0）。实证结果如下。

表7 VAR（3）模型实证结果

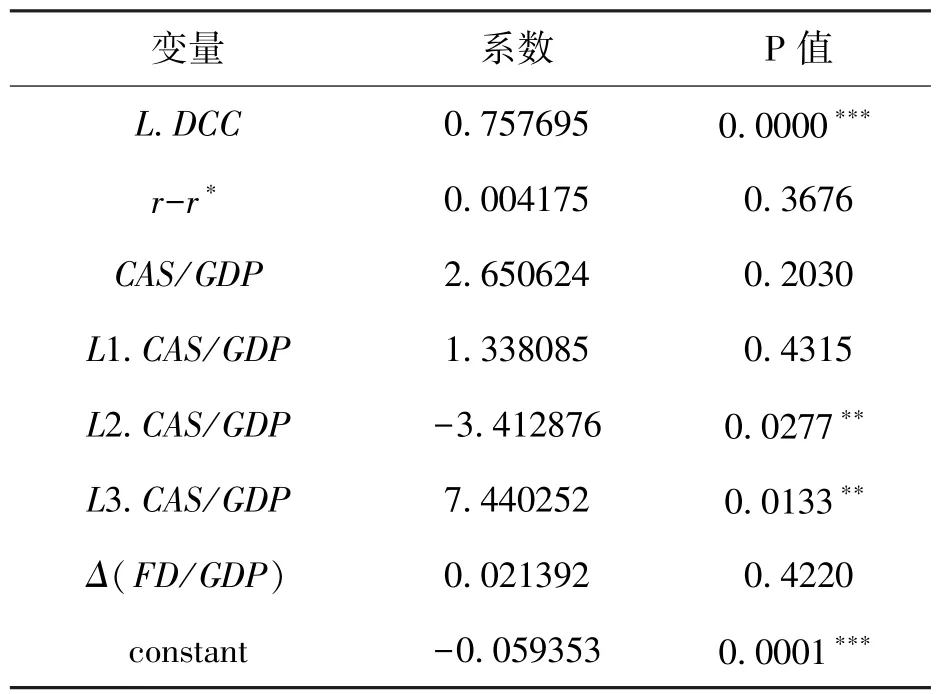
表8 ARDL 模型实证结果

ARDL 的估计结果与VAR（3）得到的结果是相似的，从滞后三阶的系数来看，中国和美国的利差（r-r*）对DCC 的影响并不显著；同时，净出口（CAS／GDP）对DCC 的影响为正，而且很显著。

从上面的稳定性检验结果可以看出，不管是改变数据选取的时间，改变变量的计算方法还是使用其他模型，本文所得到的结论都是非常稳健的。

6 结论

本文用DCC-GARCH 模型实证检验了人民币汇率和股价之间的传导机制，先计算汇率收益率序列和股价收益率序列之间的动态条件相关系数序列，然后用经常账户数据和利差数据对其进行回归。实证结果表明经常账户对DCC 序列的影响是非常显著的，而利差对DCC 序列基本没什么影响。即2008 年金融危机以来我国汇率和股价之间的关系是符合流量导向模型的，不符合存量导向模型。

汇率和股价作为两个对国民经济有着重要影响的经济变量，它们之间的联系不仅加深了我们对金融市场联动特征的认识和理解，而且对实现金融稳定有着重要的意义。金融市场之间的联动关系是风险在不同市场之间传播的主要原因，如果不能很好地控制金融风险，实体经济就会受到影响。

为了避免汇率和股价的波动对我国金融体系产生严重冲击，破坏金融稳定，我国应该加快人民币国际化进程，继续推动汇率市场化、利率自由化和资本账户开放这三大改革的步伐，保持人民币汇率水平在其长期均衡值附近的基本稳定。汇率市场化并不意味着央行完全放弃对汇率的调控，央行可以加强人民币汇率预期管理，适当地引导公众的汇率预期，从而减少汇率波动对实体经济造成的影响。同时，还需要完善衍生品市场的建设，给金融市场参与者提供更多规避外汇风险的渠道，重视外汇风险管理。

另外，逐步开放人民币资本市场，推动人民币资本项目可兑换，形成一个统一、联动的国内外金融市场。在开放资本市场的同时还需要加强对国际资本流动的监控，建立相应的监管体系，重视金融市场风险源头，建立不同金融市场之间的风险传播控制机制，避免风险在不同市场间转移。

不仅如此，还可以增大股票市场中机构投资者所占比例，优化现有的股票市场投资者结构。同时，证券公司在客户申请开户时需要做好客户风险承担能力测评，根据客户的风险承担能力推荐可以投资的产品，禁止客户投资超出其风险承担能力的金融产品。另外，还应该完善股票市场价格形成机制，提高股票市场的规范程度，深化股市改革，从而促进我国股市健康长远发展。

倡导和推动共建“一带一路”，发起创办亚投行，设立丝路基金，启动深港通、沪港通、债券通等，使我国开放型经济水平得到了显著提升，在促进自身发展的同时也给世界经济带来了新的机遇。与此同时，世界经济增长乏力，国际金融市场跌宕起伏。在这种时代背景下，我国必须规范金融市场秩序，守住不发生系统性风险的底线，维护国家经济金融安全。