基于可变指数恒虚警检测的改进算法
白鹏 陶伟
(第七一五研究所,杭州,310023)
早期雷达和声呐的信号处理能力差,接收信息直接传送至显示器,对目标的检测主要依赖于操作人员[1]。随着科技的发展,无人作战系统的提出使自主检测技术在现代雷达和声呐系统中得到越来越广泛的应用。CFAR检测作为实现自主检测的重要方法之一,也成为重点研究对象。
CFAR发展至今已有半个世纪,1968年,Finn H M等提出了单元平均恒虚警(Cell Averaging-Constant False Alarm Rate, CA-CFAR)算法[2],此算法在均匀杂波背景下性能最优。1973年,Hansen提出最大选择恒虚警(Greatest Of-Constant False Alarm Rate, GO-CFAR)[3],降低了CA-CFAR在杂波边缘的虚警概率。1978年Trunk提出了最小选择恒虚警(Smallest Of-Constant False Alarm Rate,SO-CFAR)[4],增强了CA-CFAR在多目标环境的检测性能。1983年,有序统计类 CFAR算法被提出[5]。2000年,Michael等人提出了一种可变指数恒虚警(Variability Index-Constant False Alarm Rate,VI-CFAR)检测器[6],通过前后滑窗的均值之比和二阶统计量的大小自适应的选择 CFAR处理方法。在非均匀杂波环境中取得了很好的检测效果,在多目标环境中也有一定的抗干扰能力。但是当前后滑窗都不均匀时,检测能力下降,对此胡文琳等人[7]、徐从安等人[8]、杜海明等人[9]都对VI-CFAR算法进行了改进,取得一定成果,但是仍存在不足。比如在一个滑窗存在多目标而另一个滑窗存在杂波边缘时容易产生虚警;另外,在两个强杂波间隔中的目标漏检概率高。
本文列出前后滑窗都不均匀的各种情况并进行分析,得出改进VI-CFAR处理流程图,解决了上面存在的问题,并且通过蒙特卡洛仿真验证其有效性。
1 VI-CFAR检测器
VI-CFAR算法是一种自适应算法,工作流程如图1所示。其中D是被检测单元,xi(i= 1 ,2,… ,n)和xi(i=n+ 1 ,n+ 2 ,… ,2n)分别表示前滑窗参考单元、后滑窗参考单元。该算法通过前后滑窗均值之比VMR,参考单元的二阶统计量VVI两个参数,自适应的选择CA-CFAR、GO-CFAR、SO-CFAR中的一种算法进行处理。
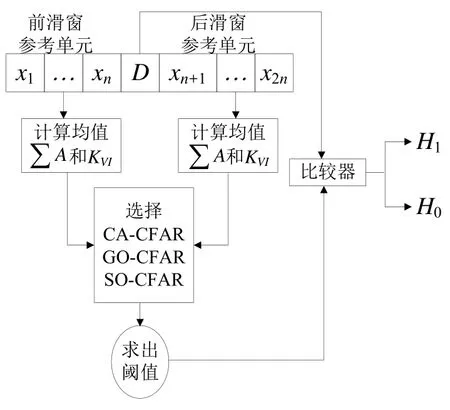
图1 VI-CFAR流程图
VMR和VVI两个参数的计算如下:


式中,A和B分别代表前后滑窗,n是一个滑窗内的参考单元数。然后用参数VMR和阈值KMR的比较作为判断前后滑窗均值是否相同的标准,用参数VVI和阈值KVI的比较作为判断滑窗是否均匀标准,判决方法如下:

定义α0为在均匀环境下被判断为非均匀环境的概率,β0为均值相同被判断为均值不同的概率,可以得到

一般情况α0不得超过虚警概率的10倍,给定α0和β0,通过蒙特卡洛方法可以求得近似的阈值KMR和KVI,具体的方法参见文献[6]。根据判断的结果选择相对应的CFAR处理方法,如表1所示。

表1 VI-CFAR对应处理方法选择
2 前后滑窗都不均匀情况分析
VI-CFAR在复杂杂波环境中能取得较好的检测效果,但是当前后滑窗都不均匀时,检测性能降低。假设单个杂波的长度大于单个窗(前窗,后窗)长度,且两个杂波间隔长度大于单个窗(前窗,后窗)长度。本文对前后滑窗都不均匀的情况进行分析,将情况归纳为四种类型,分析结果见表2。

表2 四种类型分析
3 改进恒虚警算法
对于表1中前四种情况,处理方法与VI-CFAR一致。我们分析表 1中的第五种情况,也就是VVIA>KVI且VVIB>KVI。
假设前后滑窗长都为 16个单元。对于直线型,前后滑窗都剔除2个最大值和2个最小值,反复重复此步骤,直到前后滑窗都均匀为止,此时前后窗均值相等且都均匀,对剩下的参考单元采用CA-CFAR处理。对于折线型,前后滑窗都剔除2个最大值和2个最小值,反复重复此步骤,直到前后滑窗都均匀为止,此时前后窗均值不相等但都均匀,采用GO-CFAR处理。对于盆地型和高原型,前后滑窗都剔除2个最大值和2个最小值,反复重复此步骤,但是前后滑窗至多只有一个均匀,此时将前后窗长度减小,直到成为直线型,然后按直线型的处理方法进行处理。改进的VI-CFAR流程图见图2。

图2 改进VI-CFAR流程图
首先判断前后窗是否都均匀,然后判断前后窗均值是否相等。如果都均匀且均值相等,则采用CA-CFAR;都均匀但均值不相等,采用GO-CFAR;若一窗均匀则对均匀窗采用 CA-CFAR。若前后窗都不均匀,则采用TM-TM类CFAR检测器,对前后窗分别剔除2个最大值和2个最小值。如果剔除后前后窗都均匀且均值相等,采用 CA-CFAR;如果前后窗都均匀但均值不等,采用 GO-CFAR;如果前后窗不都均匀,且滑窗大于4个单元,则继续采用TM-TM类CFAR检测器,对前后窗分别剔除2个最大值和2个最小值,重复之前的流程。如果滑窗小于4个单元,则对前后滑窗都减少4个单元,回到第一步重复流程。
4 仿真分析
前后滑窗各取16个单元,选取参数KMR=2,KVI=2,虚警概率取10-6,多目标非均匀杂波环境下的仿真结果如图3所示。我们对多目标局部进行放大得到图4,可以看出改进 VI-CFAR算法性能优于 VI-CFAR。VI-CFAR抗干扰能力较差,容易出现漏检。

图3 多目标非均匀杂波环境仿真

图4 多目标局部放大
我们对杂波边缘进行放大,如图5所示,可以看到前窗存在干扰目标,后窗既存在干扰目标也存在杂波边缘,此时改进VI-CFAR有效避免了杂波边缘的虚警,而VI-CFAR则不能。

图5 多目标杂波边缘局部放大
设定虚警概率为 10-6,前后滑窗长度都为 16个单元,采用蒙特卡洛仿真100 000次。在均匀杂波环境中,CA-CFAR理论性能最优,VI-CFAR和改进VI-CFAR性能和CA-CFAR基本相同,结果如图6所示。

图6 均匀环境下各检测算法性能
在多目标环境中,前后滑窗都存在干扰目标,CA-CFAR性能下降最严重,VI-CFAR性能较好但是低于改进VI-CFAR的性能,结果如图7所示。

图7 多目标均匀环境下各检测算法性能
多目标非均匀杂波环境下,前后窗都可能存在干扰目标,且存在杂波边缘,仿真前窗2个干扰目标,后窗存在杂波边缘,此时改进VI-CFAR效果最优。CA-CFAR和VI-CFAR的性能完全达不到要求,仿真结果如图8所示。

图8 多目标非均匀环境下各检测算法性能
5 结论
本文对可变指数恒虚警算法提出了改进,对于前后滑窗都不均匀的各种情况进行分析,并给出算法的流程。对于 MVI-CFAR、OSVI-CFAR等方法在前后滑窗既存在多目标又存在杂波边缘的情况下性能下降的问题,本文提出的改进可变指数恒虚警方法能够有效提高检测器的检测概率。但是此算法只适用于一维检测处理,对于二维VI-CFAR前后滑窗均值不等且不均匀的情况,仍需进一步讨论和研究。

