基于FFNN的垂直阵被动定位技术研究

张巧力 刘福臣

（声纳技术重点实验室 第七一五研究所，杭州，310023）

随着大数据技术的迅速发展，基于深度学习的数据驱动方法逐步应用于水声领域的目标检测、定位和识别等。水下目标定位是通过水听器阵列接收到的声波信号来估计目标声源的空间位置。该项技术一直是探索海洋的研究重点和热点。被动定位技术以其优良的隐蔽性、高安全性，在军事和民用领域都具有广阔的应用前景，是声呐技术发展的重要方向之一。经过国内外研究人员几十年的深入研究，以MFP为代表的模型驱动方法相关理论和技术取得了丰硕成果[1-3]。此类方法将声传播模型与阵列信号处理结合起来，利用水声信道特性获取优良的定位性能，但通常受到海深、声速剖面等因素的影响，存在失配情况，或声传播模型参数未知等情况，影响定位性能。

不同于模型驱动定位方法，以深度学习为代表的数据驱动方法直接从数据中寻找特征，无需海洋环境先验信息，避免了环境声场理论建模引起的环境失配的影响。从文献[4]可知，人工神经网络第一次应用于水下目标定位是在 1991年，Steinberg和Beran等利用单层神经网络技术对均匀介质中的点声源进行深度估计；同年，文献[5]中 Ozard和Zakarauskas等仿真实现了基于人工神经网络的声源距离-深度估计。2017年H Q Niu等人引入了FFNN、支持向量机、随机森林等方法，将定位问题转化为分类问题，取得了不错的定位效果[6-7]。

本文利用美国海洋物理实验室1996年5月在距 Point Loma约 12 km处进行的一次浅海实验（SWellEX-96实验）研究垂直阵定位问题[8]，详细分析了该实验获取的垂直阵数据，比较了基于FFNN定位和基于简正波模型的MFP的定位性能。

1 匹配场处理

常规匹配场定位属于模型驱动方法，它是利用预知海洋环境参数与基阵相关参数，基于声传播模型仿真声场，计算拷贝场向量，利用实际基阵测量数据与之匹配，匹配输出距离-深度模糊表面，从而实现目标的距离和深度估计[9]。MFP的定位的模糊度平面B由互谱密度矩阵R和拷贝向量组成ω：

式中，ω表示拷贝向量，φ表示声源位置参数，（·）H表示共轭转置；L表示快拍数；Pl表示第l个快拍下基阵频域数据向量。

对于宽带信号，可采用频间非相干法，将该信号分为若干个窄带，对每个窄带单独处理得到模糊度平面，再进行累加平均。

2 前馈神经网络

FFNN属于数据驱动方法，由大量的人工神经元相互连接进行计算，根据训练样本，通过调节神经元之间的权值来输入数据进行建模，最终具备解决实际问题的能力，神经网络在模式分类、聚类和回归拟合等领域广泛应用。本文将目标定位问题转换为分类问题处理。图1为典型的单隐藏层FFNN结构。

工作原理主要分为两个过程：工作信号前向传播和误差信号的反向传播。输入的工作信号从输入层经隐藏层，传向输出层，最后产生输出信号，工作信号前向传播过程中，层与层之间连接权值固定不变。网络输出信号与期望信号存在差异，两者之间差值即为误差信号[10-11]。误差经代价函数计算后，由输出层逐层向输入层反向传播，通过误差反馈来更新调节层与层之间连接权值，更新的权值用于下一次工作信号前向传播。通过周而复始的学习，权值不断修正使神经网络实际输出接近期望输出。

图1 FFNN结构示意图

2.1 信号预处理

本文使用实向量化的采样协方差矩阵（Sample Covariance Matrices，SCMs）作为FFNN的特征输入[7]。为了减小声源振幅的影响，Q个阵元垂直阵接收复声压进行范数归一化操作：

采样协方差矩阵根据L个快拍数据平均计算得到

在文献[6-7]中，为满足FFNN实值输入要求，选取SCMs上三角及对角线的实、虚部值构成特征向量X，维度为但由于SCMs是复共轭对称矩阵，其对角线的虚部始终为 0，因此本文提出了新的实值向量化方案，新的特征向量X由SCMs的对角线实、虚部及对角线实部构成，减少了特征向量X长度，则维度变为其中Nf为频点数（窄带信号取Nf=1；宽带信号取Nf≥ 2 ）。

2.2 标签处理

假设声源距离范围为（rmin,rmax］，采用等宽分箱离散化处理，将声源距离等分为K类，即

则第n个样本实际距离Rn所属类别tn,real定义如下

训练过程：将样本实际距离所属类别tn,real以独热编码方式（One-Hot Encoding）处理，映射到1×K的二进制标签向量，作为FFNN的输出。

测试过程：测试样本距离估计结果，用 FFNN预测距离所属的类别tn,pred所对应的距离区间的中间值表示（下文简称预测类别距离）：

2.3 网络结构搭建和参数选取

本文构建了单隐藏层的 FFNN，隐藏层神经元个数设为256，选择Sigmoid和Softmax函数作为隐藏层和输出层的激活函数，并在其中加入Dropout层预防过拟合现象，神经元丢失率设为0.5。网络以Tensorflow为底层的高级深度学习链接库Keras完成训练与预测[12]，选择Adam算法作为优化器，学习率为0.001，交叉熵（Cross-Entropy）作为损失函数，最大训练次数为1 000次。

为了量化定位性能，本文引入平均绝对百分比误差（Mean Absolution Percentage Error，MAPE）评价指标，定义如下

式中，Nall为总样本数，ri,pred和ri,real为第i个测试样本预测距离和实际距离。

2.4 仿真验证

2.4.1 仿真条件

仿真采用SWellEx-96实验的浅海环境参数，包含海水层、沉积层、泥岩层以及半无限空间，含21个元的垂直阵列布放深度范围在 94.125～212.25 m之间，阵元采样率 1.5 kHz，如图2所示，使用KrakenC数值计算仿真数据。

图2 SWellEX-96实验浅海环境参数模型

仿真考虑窄带声源，中心频率为94 Hz，信噪比为0 dB，假设声源深度固定不变，深度设为54 m。本次仿真声源与垂直接收阵范围为（0,10]km，训练样本的距离采样间隔为5 m，训练集（包含验证集，占比20%）共有2 000个样本；为了测试样本与训练样本不重叠，测试样本的距离采样间隔增加到51 m，则测试集共有196个样本。本次仿真将距离变量离散为100类。

2.4.2 仿真结果分析

网络分别以文献[6-7]提出的SCMs实向量化方案和本文提出的新方案来构建特征向量，建立两个FFNN，分别训练和测试。两个模型的输入层神经元个数分别设置为21× 2 2×1= 4 62和21× 2 1×1= 4 41。在其他参数条件均相同的情况下，两个模型的所需训练超参数（Hyper-Parameters）总量分别为144 228和138 852，一般来说训练超参数越大，模型越复杂。图3展示了上述两个模型下测试集样本距离估计结果，计算MAPE分别等于1.32和1.30。结果显示，两种情况下均有良好的定位性能。相同条件下，本文提出的SCMs实向量化方案在不影响定位效果基础上，降低了模型的复杂度。

图3 两个模型下测试集的定位结果

3 海试数据验证

3.1 实验描述[8]

SWellEX-96共包含S5和S59两个航次，实验环境参数如图2所示。本文使用该实验S5航次的垂直阵接收的数据进行比较和验证，S5航次一共拖曳了深（54 m）和浅（9 m）两个声源，声源移动速度约为2.5 m/s，共记录了75 min数据。实验使用的垂直阵有22个水听器，采样频率为1.5 kHz，布放深度在94.125～212.25 m之间，由于有一个水听器没有正常工作，仅使用21个水听器的测量数据。

3.2 实验数据处理及结果分析

3.2.1 MFP定位

本文考虑深（54 m）声源定位，选取 235 Hz作为窄带声源的中心频率，{112,235,388}Hz三个频点作为宽带声源频率，设搜索海域的距离范围是0～10 km，间隔为50 m；深度范围1～200 m，间隔为1 m，使用简正波模型描述拷贝场，由KrakenC程序进行仿真，声压场的互谱密度矩阵使用3个1 s的快拍数据计算获得，利用Bartlett算法估计出水下目标声源位置。图4为窄带和宽带声源的距离估计结果。结果表明：在环境匹配条件下，距离 2 km以上的声源MFP整体定位效果不错，对于在0～2 km范围内的声源定位效果较差，主要原因是简正波模型不适合近场条件下声场建模。相比较窄带声源，宽带声源定位性能略优。

图4 MFP在测试集上的定位结果

3.2.2 FFNN分类器

该实验共记录了75 min数据，每1 min给出了该时刻的GPS定位信息，共76个位置信息作为测试集。相邻两个测试样本之间，每间隔4 s作为一个训练样本点，距离值通过插值获得，共1 050个插值点作为训练集。对于每个采样点，各个选取频率及各位置下的SCMs由3个1 s快拍数据平均计算获得。这里同样将搜索范围设置为0～10 km，此距离范围内等宽分箱为K=100个距离类别。图 5为窄带声源和宽带声源在FFNN方法下的距离预测结果。结果表明：无论窄带还是宽带声源，相较于MFP，FFNN的定位性能均明显提升，尤其是在近场条件下的声源定位。

图5 FFNN在测试集上的定位结果

为了更加准确直观定量比较两种方法，表1给出了窄带和宽带声源分别在MFP和FFNN两种方法下的MAPE，无论窄带还是宽带声源，FFNN方法下的MAPE远远小于MFP，FFNN定位性能优于MFP。通过表1纵向对比可以发现，无论FFNN还是MFP方法，宽带声源的MAPE均小于窄带声源，这是由于相较于窄带声源，宽带声源提供了更多信息，因此会获得更优的定位性能。

表1 窄带和宽带声源分别在不同方法下的MAPE

图6为0～10 km范围内宽带声源在两种方法下的距离估计结果的绝对误差。MFP和FFNN的平均绝对误差分别为1.26 km和0.12 km，方差分别为2.81和0.04。FFNN大幅度减小了距离估计绝对误差，除个别误差较大（1.8 km左右），其余绝对误差都控制在0.3 km以内。相比之下，FFNN较MFP具有更高的定位精度和较好的稳定性，尤其是近距离声源的距离估计。

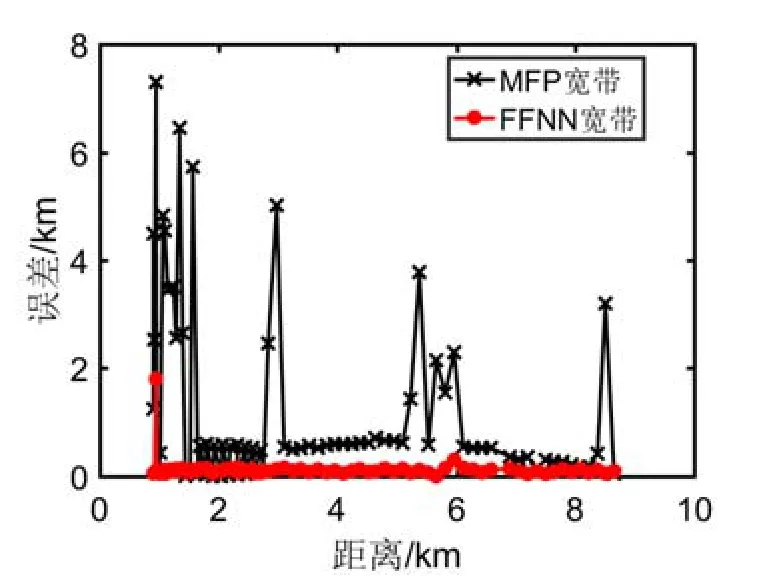
图6 0～10 km范围内距离估计结果的绝对误差

4 结论

本文通过 SWellEX-96海试数据处理验证，对比了FFNN为代表的数据驱动定位方法和传统MFP为代表的模型驱动定位方法的性能。结果表明，在海洋环境已知条件下，无论是窄带还是宽带声源，FFNN具有更好的定位性能，那么当在环境参数未知或失配条件下，数据驱动方法提供了非常好的解决思路。

本文方法主要针对单目标问题。对于多目标问题，如果能够将目标声信号频段区分开来，可以视为多个单目标问题处理，则此方法仍然使用，如果目标频段重叠严重，不能分辨，那么该方法就不适用了。