流量计用超声波探头的研制

刘细宝 钟利民 郁涛 楼成淦 陈立新 刘文静

（杭州瑞利超声科技有限公司，杭州，310023）

超声流量计是基于超声波在流动介质中传播速度等于被测介质的平均流速与声波在静止介质中速度矢量和原理开发的，先依据时间差来测量流体的流速，进而计算出流体的流量[1]。流量计主要由换能器和转换器组成，有多普勒法、速度差法、波束偏移法、噪声法及相关法等不同类型[2]，并具有精度高、功耗小、抗干扰能力强、可不直接接触被测介质、防爆、安装方便、无需切管（不影响正常生产）、无需缩径等诸多优点，广泛应用于石油、化工、冶金、电力、给排水等。流量计的关键部件之一即是超声波探头，超声波探头的信噪比和性能优劣，直接决定了流量计计量是否准确。由此，本文详细介绍了一种超声波探头的结构设计和装配工艺，以期降低流量计的测量误差。

1 结构设计与理论计算

本文中的超声压电振子是由一片压电陶瓷圆片和一片金属圆片经导电胶粘结起来做成弯曲圆盘式复合振子，如图1所示。压电陶瓷圆片和金属圆片必须足够平整才能粘结牢靠。

图1 超声压电振子的结构示意图

弯曲振动频率fr取决于振子的径厚比、材料性质以及边界支撑条件[3-4]。

式中，A为边界支撑条件决定的常数，波节固定时A=0.467；周边固定时A=0.233。

本文采用周边固定法，故A取0.233。t为复合振子厚度，m；r为复合振子的半径，m。当压电陶瓷片的半径r1与金属片的半径r2之比X＞0.7时，才能使振子的阻抗比较低，当X=1时最佳。Y为两片材质的合成杨氏模量，Pa；ρ为两片材质的合成密度，kg/m3；σ为两片材质的合成泊松比。

在边界条件固定的情况下，频率的变化与t/r2成正比。在可闻声域内，这类振子直径多在Φ10～Φ50 mm，总厚度在0.4～0.5 mm的范围内[5]。本文弯曲圆盘式复合振子的直径为Φ14 mm，即r=7 mm，复合振子总厚度为t=2.225 mm，其中压电陶瓷圆片的厚度t1=1.5 mm。该振子沿厚度方向振动。压电元件圆形薄片直径约为厚度的 10倍，保证了振动的方向性。

金属圆片宜选择线性膨胀系数与压电陶瓷最接近的金属。压电陶瓷的平均线性膨胀系数约为αl≈2.5×10-6/℃（20℃），经查阅文献[6]并验证，牌号为4J36的殷钢（Invar Steel）在居里温度（230℃）以下平均线性膨胀系数约为αl≈2.5× 10-6/℃（20℃），且殷钢坚硬，导电性能好，故金属圆片材料选用殷钢。已知压电陶瓷的密度ρ1=7.6×103kg/m3，殷钢的密度ρ2=8.1×103kg/m3。

压电陶瓷圆片选用接收型p14压电材料具有较高的压电应变常数d33=6.4×10-10（C·N-1），意味着用它制作的超声压电振子接收灵敏度较高。该型材料的自由相对介电常数为

式中，ε0为真空（或自由空间）的介电常数，ε0=8.85×10-12（F·m-1），ε为绝对介电常数。绝对介电常数ε与元件的电容Ct，电极面积S和电极间距t1之间的关系为

2 换能器参数估算

假设接收换能器在液体中收到的声压为F，则弯曲圆盘式复合振子产生电荷：

弯曲圆盘式复合振子采用单片元件，则弯曲圆盘式复合振子产生电压：

将式（3）代入，得

将式（2）代入，并假设弯曲圆盘式复合振子元件为全电极，则

代入已知参数，得

假设前置功放电路电压放大倍数为β，则

3 建模仿真分析

利用有限元声学仿真软件COMSOL建模仿真。首先建立模型，网格划分后输入材料参数杨氏模量Y、泊松比σ和密度ρ，最后计算振型图、应力分布图、位移图和导纳图，见图2～4。因为圆是对称的，为了节约内存和计算量，如图2所示，只仿真了一个10°的扇形。由图3可知，前辐射面圆心处应力比较集中。图4位移图表明该振子输出位移较大。图 5为 COMSOL仿真的导纳图，仿真范围为 60 kHz～1.6 MHz，步长为3 kHz，仿真结果表明该振子的特征频率即谐振频率为1.149 MHz。

图2 振型图

图3 应力分布图

图4 位移图

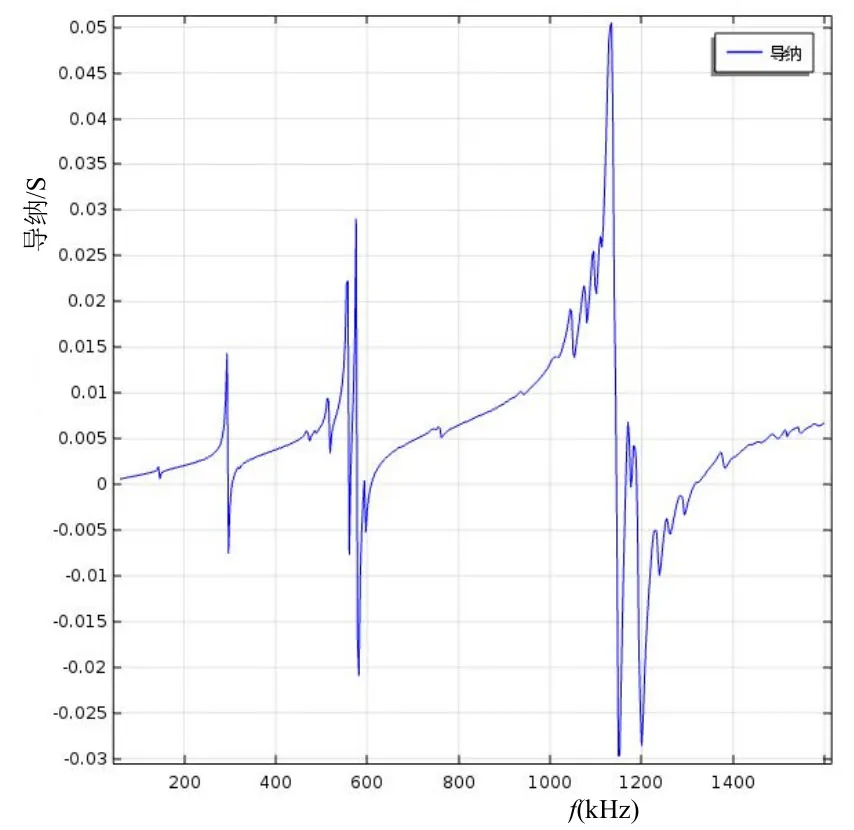
图5 导纳图

4 封装测试结果与讨论

加工的结构件及元件如图6所示，粘接好的振子如图7所示，利用PCB板在压电元件后面做空气背衬，板后面再灌胶水密封。

图6 结构件及元件图

图7 振子照片

装配时注意保压至胶水完全固化为止，排尽气泡，胶水均匀，压电陶瓷元件和结构件的同心度、平整度一致，否则阻抗偏高，容易打火、开裂导致成品率下降。

超声压电复合振子经Agilent 4294A精密阻抗分析仪测试曲线见图8，谐振频率fr≈1.027 64 MHz，与仿真值1.149 MHz接近。谐振阻抗为75 Ω，静态电容C0=1.76 nF。依据文献[7]进行样品标定测试，测试结果列于表 1。测试数据表明，配置该超声波探头的流量计测量误差在1%以内。

表1 流量检测数据

图8 阻抗曲线测试图