民机空调系统部件不完全维修决策优化

■ 李景奎 齐一蕊 程云开 张俭/沈阳航空航天大学 中国南方航空股份有限公司沈阳维修基地

0 引言

随着国内民航事业的崛起，飞机成为人们出行的重要工具，各航空公司飞机维修任务急剧增加，飞机维修通常存在“维修不足”与“维修过剩”的现象。为了提高维修效率，制定合理的维修计划，国内外众多学者对维修优化问题进行了深入研究。

Barlow[1]提出了最小维修的概念，并应用于设备零部件替换问题；Malik[2]首次将改善因子引入设备预防维修研究中，提出有效役龄的概念；Grigorie[3]研究了特定时间内的维修任务分配问题。赵永强[4]在考虑可靠性和维修成本的基础上，假设故障数据符合二参数威布尔分布，对维修模型进行了分析；宋之杰[5]在可用度和维修成本分析的基础上，以二参数威布尔分布模型为依据，运用枚举法求解维修次数与周期；张民悦[6]建立了弹性周期预防维修模型，求解了最优弹性维修周期。

将维修故障模型假设为二参数威布尔分布模型，计算精度不够准确，计算结果存在误差。为解决这一问题，本文假设空调系统部件的故障数据服从三参数威布尔分布，通过引入动态改善因子，对空调系统部件进行不完全维修分析，并以单位时间总维修成本最低为目标、以可靠寿命为约束建立优化模型，通过MATLAB遗传算法编程，获得最优维修次数与维修间隔。

1 不完全维修模型

1.1 模型描述

设备维修[7]可分为最小维修、完全维修与不完全维修。最小维修能够使设备恢复到故障前的状态，设备能够继续运行，但是故障率不变；完全维修能够将设备恢复到初始状态，是一种理想的维修方式；不完全维修的效果介于最小维修与完全维修之间，是目前设备维修中采取的最常见的维修方式。

1.2 基本假设

为简化分析模型，对设备部件不完全维修模型做如下假设[8]：

1）不完全维修不能使部件性能恢复到最初状态，不完全维修后部件故障率处于零故障率与维修前故障率之间。

2）维修周期内，部件发生临时故障，对部件进行最小维修，最小维修后部件的故障率不改变。

3）经过一定维修次数后，对部件进行预防性更换，部件恢复如新，故障率为零。

2 构建不完全维修优化模型

2.1 改善因子

设备经过维修后，性能并不能够恢复如新，随着维修次数的增多，设备维修后的性能恢复程度也会逐渐降低，为了表示设备维修后性能的恢复程度，本文引入改善因子δi[5]，表达式如公式（1）所示。

式中，N为预防性维修次数；Cpmi为预防维修成本；Cpr为预防性更换成本；a为维修成本的调节系数，且1≤a≤Cpr/Cpmi，维修成本的调节系数用来调整不同设备维修成本率所反映的改善程度；b为预防性维修次数的调整参数，0＜b＜1。a与b的值根据设备的运行状态及其故障历史资料来确定。

2.2 有效工龄及故障次数

由公式（1）可知，改善因子的值随着维修次数的变化而变化，改善因子的值越大，表明设备经过维修后使用寿命减少得越少，剩余寿命增加得越多。所以，随着改善因子值的不同，设备的有效役龄也不同。

假设设备的维修周期为h，每次预防性维修后的有效役龄都受到影响，则设备第一次维修前后的有效役龄分别是[3]：

即经过不完全维修后设备的剩余役龄增加了δ1h。

设备第二次预防性维修前后的有效役龄分别为：

以此类推，可知设备在第i次预防维修前后的有效役龄分别是：

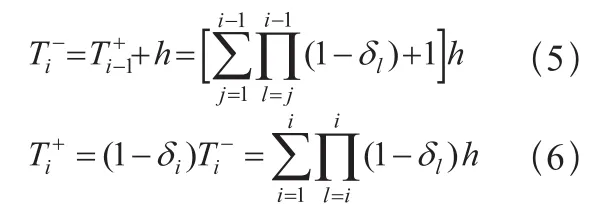
通过分析可知设备第i个维修周期的有效役龄为：

为了保障设备安全运行，每个维修周期内出现的临时故障都要进行小修，小修次数是影响维修费用的一个重要因素，因此第i个维修周期内，系统的故障次数为：

式中，λi（t）为服从三参数威布尔分布的设备故障率，由此可知设备在第i个维修周期内的故障率函数表达式为：

其中，β＞0为形状参数，α＞0为尺度参数，γ≥0为位置参数。

2.3 维修成本及维修时间

以单位时间内总维修费用最低为目标、以设备的可靠寿命为约束构建优化模型。其中，总维修费用由最小维修费用、不完全预防维修费用以及更换成本三部分构成。设备总寿命时间由运行时间和总预防维修时间两部分构成。

1）最小维修成本

为了减少时间成本，一般在设备停车时间进行最小维修，因此最小维修时间可以忽略不计。

2）预防维修成本及时间

随着设备运行时间的增加，设备磨损情况加重，tpmi的值也会增加。因此，假设tpmi=（1/η）·i·h，其中 1/η为预防维修的时间调整参数。

3）预防性更换成本

为了保证设备安全运行，设备在第N次维修时将进行预防性更换，预防性更换将产生一次固定的预防性更换成本，记为Cpr。

综上，设备的总维修费用为

设备的总维修时间为

最终确定以单位时间内维修费用最少为目标、可靠寿命为约束的优化模型，表达式为：

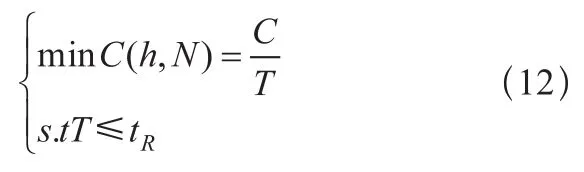
其中，tR为可靠度函数，其表达式为：

3 算例分析

以某航空公司空调系统流量控制活门（FCV）的维修任务[9]为研究对象，进行算例分析验证。

FCV的故障数据符合三参数威布尔分布，其模型参数设置如表1所示。

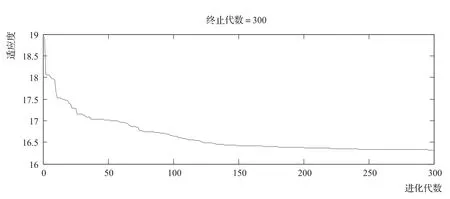
图1 遗传算法适应度曲线

表1 三参数威布尔分布参数估计

由此可得FCV可靠寿命为

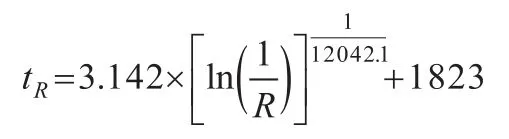
FCV维修费用及时间计算参数如表2所示。

设置改善因子的维修成本调节系数为a=1，维修次数调节系数为b=0.005；要求系统的可靠度不低于0.85。

根据优化模型进行MATLAB遗传算法编程，采用种群规模为100、交叉算子为40、交叉概率为0.8、变异算子为40、变异概率为0.3、迭代次数为300的参数设置，计算结果如图1所示。

由图1可知，迭代进行到200次后，优化算法寻优过程趋于稳定，证明了优化模型的可行性。寻优计算结果显示，FCV在全寿命期间进行10次不完全维修、每次维修间隔为6126FH为最优维修次数与维修间隔。由维修大纲（MRBR）可知，FCV的维修任务间隔为6000FH，误差率为2.1%，误差率在合理的范围内，再次验证了本优化模型的可行性与正确性。

4 总结

在考虑了系统部件故障数据服从三参数威布尔分布的基础上，建立了费用率优化模型，根据遗传算法，获得了最优维修次数与维修间隔。以民用飞机空调系统部件为例，对优化模型进行验证，计算结果证明了优化模型的可行性与正确性，为民机维修提供了理论支撑。

表2 参数设置表