突发事件下多目标应急救援物资配送路径规划
康 斌, 刘 权, 黄 健, 龚建兴
(国防科技大学智能科学学院,长沙 410073)
近年来,突发事件已经成为危害人类安全的主要因素。突发事件发生后,应急救援物资的指挥调度是救援工作的核心,即核心环节就是应急物资的配送[1]。面对突发事件中可能出现的各种不确定情况,例如交通路网结构的破坏、车辆运力不足、道路阻断修复和车辆类型限制等情况,决策者需要决定如何快速、有效地对应急救援物资进行优化配置,使得配送时间最短、需求未满足率最小、成本最低等。由于应急救援决策受救援时间和应急物资数量等因素约束,如何选择合适的路径提高物资配送的效率和效果是应急决策者面临的重大问题。
针对应急救援物资的配送问题,中外研究学者做了许多相关的研究。吕游等[2]以最小成本花费为研究目标,建立基于硬时间窗的车辆配送优化模型,引入排队策略思想优化实时路径,通过实验验证其合理性。Cao等[3]以最小救援时间、最小成本和最大救援效果为目标,建立应急救援车辆路径优化模型,提出一种基于蚁群算法的非支配解排序遗传算法(non-dominated sorting in genetic algorithmsⅡ,NSGAⅡ)和一种基于随机交叉和变异的NSGAⅡ混合遗传算法。俞武扬[4]以配置总成本最小为目标,考虑阻断道路数量和需求量两个参数,建立两阶段应急救援物资鲁棒配置模型,将二次规划模型转化为整数混合模型并提出Benders分解算法。段满珍等[5]考虑在不确定通行能力限制条件下,分析公交疏散问题,研究了上层最优转向策略和下层救援时间最短路径。刘波等[6]以最小车辆调配时间和最小车辆成本为目标,在时间窗和道路通行可靠性限制情况下,建立双层鲁棒优化模型。王晶等[7]以最大配送效率为目标,充分考虑道路中断和通行可靠性降低对应急救援配送路径的影响,建立道路修复和道路可靠性选择集成优化,并提出了多吸引子的粒子群算法对其求解。
目前,在应急救援物资配送优化目标的考虑上,多数文献以时间和成本花费为研究目标,主要集中在提高配送的效率方面,在配送效果方面研究比较少。现以最小化最晚服务结束时间和最小化需求未满足率为目标,在道路对车型限制、道路阻断修复和道路可靠性约束条件下,建立多目标优化模型,既考虑配送效率又兼顾配送公平性效果,更为满足实际救援情景下的应急资源配送路径规划需求,以期为突发事件下决策者快速选择有效救援物资调度方案提供决策依据。
1 问题描述与模型构建
1.1 问题描述
突发事件下,面对时间紧迫,道路情况复杂等多种因素,如何安全高效地将应急救援物资配送到需求点成为决策者需要重要考虑的问题之一。为了符合实际救援物资配送要求,考虑实际灾害情景对救援物资配送车辆路径规划的限制因素。①存在道路受突发事件影响而受损以及道路自身结构如桥梁、窄道等因素限制,为保证车辆能够顺利通行,需考虑道路路况对车型的限制;②灾害发生后,部分道路损毁导致路段完全无法通行,为提高配送效率,需考虑对部分道路进行抢修;③道路受次生灾害影响存在一定的安全风险,需考虑道路的可靠性因素,可依靠技术检测或受灾程度分析等手段得到道路可靠性等级信息。优化目标在考虑应急物资可用量和车载容量限制条件下,确定最佳配送方案使得最晚车辆服务时间最短和物资需求点的需求未满足率最小。
1.2 问题假设
(1)配送过程中忽略配送车辆故障和最大行驶距离的影响。
(2)应急救援道路网络情况已知。
(3)仅考虑车辆配送情况,需要飞机、轮船等其他运输方式才能到达的需求点不做考虑。
(4)道路修复完成之后可靠性为1。
(5)需求点位置不变,且物资在需求点不能转移。
(6)救援物资仅考虑一般生活物资并且可以混装,不影响装卸货时间。
1.3 参数设置和变量说明
应急道路网络表示为G=(V,A,L),其中,V(i∈V)表示所有节点,其中i=0表示配送中心,i=1,2,…,n表示需求点,n为需求点的数量;A为可用链路集合;L为失效链路集合,l∈L。K为车辆集合,k∈K。Q为应急物资可用量。Qij为车辆从i点出发,到达j点后,配送给j点的物资量(i,j)∈A。QAi为配送前i点的应急物资可用量。QFi为配送后点i处应急物资持有量。Qk为在应急配送中心处车辆k的装载量。wik为车辆k给需求点i处运送应急物资的数量。Di为需求点i处应急物资需求量。Sik为车辆k在点i处的服务时间。nh为工作效率,即每小时物资的装载量或者卸载量。rij为链路(i,j)∈A的安全通过概率,rij∈[0,1]。rk表示车辆k的最大容量。M为车辆类型(M为整数,越大车辆越大型)。KMij为链路(i,j)∈A允许通过M及其以下类型的车辆,即车辆限定值。tl为道路l抢修完成时间。VAik为0-1整数变量,如果车辆k在需求点i处可用为1,否则为0。VFik为0-1整数变量,如果点i是车辆k所服务路线上的最后一个节点为1,否则为0。xijk为0-1整数变量,车辆k通过链路(i,j)∈A为1;否则为0。yik为0-1整数变量,车辆k经过需求点i为1,否则为0。
1.4 多目标车辆路径优化模型
车辆在链路(i,j)的运行时间tijk取决于链路的距离dij以及车辆的最大限制速度vij和平均运行速度vk,即tijk=dij/min(vij,vk)。车辆k在需求点i的卸货时间Sik=wik/nh由此,车辆k在需求点i的服务结束时间ti=tijkxijk+Sikyik。
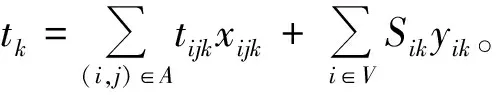
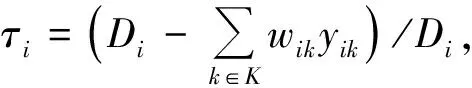
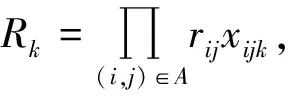
应急救援物资配送优化模型如下:
minZ1
(1)
minZ2
(2)
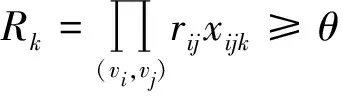
(3)
s. t.
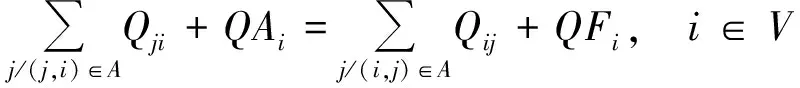
(4)
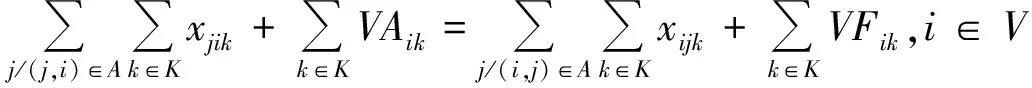
(5)
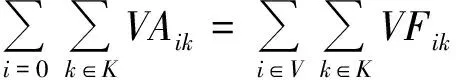
(6)
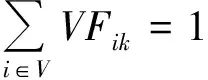
(7)
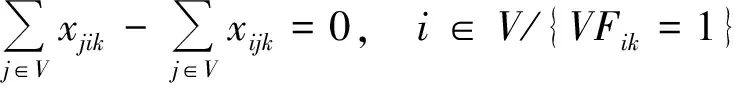
(8)
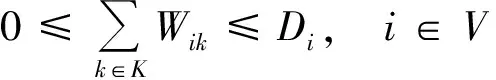
(9)
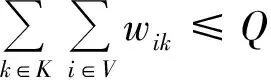
(10)
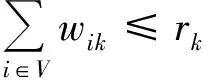
(11)
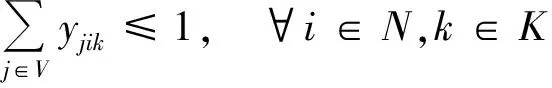
(12)
式(1)表示最小化车辆最晚服务结束时间;式(2)表示最小化需求未满足率;式(3)表示安全通过概率不小于规定值;式(4)表示从配送中心运出的物资总量等于需求点的配送量;式(5)为在各节点处车流量均衡;式(6)表示车辆总数不变;式(7)表示服务结束时一个车辆可以且仅可以停留在一个节点上;式(8)表述车辆到达一个节点(除路线上最后一个节点外)后必须从同一个节点离开;式(9)表示车辆配送给需求点的物资量不超过其需求量且非负;式(10)表示配送到需求点的物资总量不超过应急物资可用量;式(11)表示车辆装载量不超过车载容量;式(12)为子回路规避,同一辆车只能服务同一个需求点一次。
2 模型求解
2.1 数据获取
地震等突发事件发生后,第一时间无法准确获得环境信息具体的数值,使得面向数据决策的数据获取具有较大的难度。利用谷歌地图、高德地图等软件获取相关路网信息,同时结合专家评估法[8]对路网进行评估。具体评估方法如下。
(1)请专家对震后路网结构中被破坏的路段进行评估,估计出每条路段抢修完成平均时间tl,物资消耗量暂不考虑在内。
(2)对所有路段的通行可靠性进行估计;根据车辆类型差异,给出路段对车辆的类型限制要求。
2.2 模型层次化求解
应急救援物资配送路径规划涉及两层优化问题:①路网层问题,在道路对车型的限制条件下,通过车型对路网结构进行更新,每类车型对应一种路网结构,保证在满足最优目标条件的同时又能够成功完成配送任务;在道路抢修时间已知情况下,确定道路能否在车辆到达前抢修成功,保证车辆顺利通行;②路径层问题,在以上分析的基础上,车辆分配给不同的需求点,配送路径不同,同时分析配送路径可靠性,确定所有车辆的最佳配送路径,使得配送方案最优。
2.2.1 路网层优化问题
首先假定整个路网道路情况完好,根据车辆类型限定值KM,更新整个道路路网的结构,得出不同类型车辆所对应的路网。每条路段(i,j)存在安全通过概率rij,在满足rij>θ的条件下,计算任意两点之间最短路径dij。采用Floyd算法[8]对路网层进行求解,得到逻辑层面的全连通路网结构。路网层优化结果作为路径层的输入,保证车辆顺利完成配送任务。
2.2.2 路径层优化问题
不确定路网情况下车辆路径分配属于典型的NP难问题[9]。理论证明,采用遗传算法解决NP难问题能够得到较好的可行解,因此采用非支配解排序的遗传算法(NSGAⅡ)解决应急救援物资车辆配送路径规划的多目标优化问题,引入部分映射交叉(partial-mapped crossover,PMX)和优先邻点混合交叉算子,提高局部搜索能力。NSGAⅡ将应急救援物资配送同受损道路修复,道路对车辆类型限制和道路安全系数进行综合优化,使得最终输出的应急救援物资配送路线达到最优。
2.3 NSGAⅡ设计
NSGAⅡ算法思想[10]:首先,采用随机方式生成初始种群,通过交叉变异生成新一代的子种群,将父代种群和子代种群合并,经过快速支配排序并计算所有个体的拥挤度,最后由精英选择策略选择合适种群作为新一代父代种群,直到满足结束条件。
2.3.1 染色体编码
应急救援物资车辆配送路径规划问题是车辆从配送中心出发经历不同的需求点,得到车辆行驶路线。考虑到车辆编号和需求点编号为整数序列,因此在NSGAⅡ中采用整数编码方式。每条染色体由两个字串组成,即X=[X1,X2]。因为车辆总数为k,需求点总数为n,所以X1包含k个元素,X2包含n个元素,两个字串产生方式为随机产生,所有车辆都从一个配送中心出发,忽略配送中心在染色体中所占位置,染色体的总长度为k+n。染色体结构如图1所示。
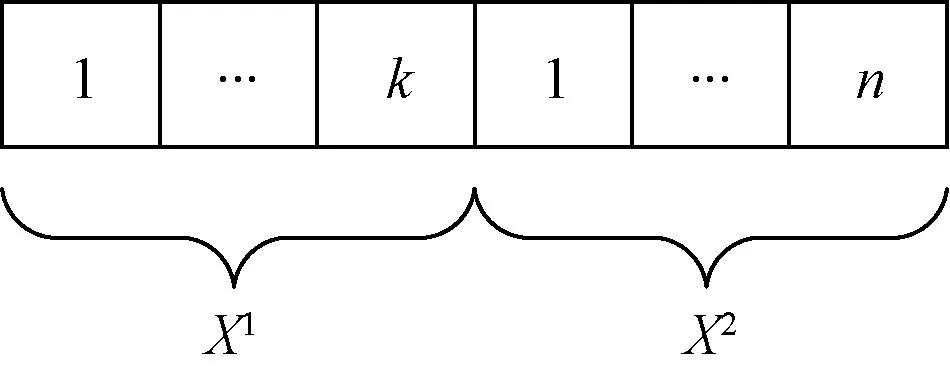
图1 染色体结构Fig.1 Chromosome structure
2.3.2 种群初始化
(1)染色体中X1的一个基因位代表一辆车,检测该基因位车辆所属类型,输入对应的路网结构。
(2)X1中的第一个基因位表示所对应的车辆首先会到达X2的第一个基因位所代表的需求点,由该辆车为该点进行配送,并检验是否满足道路可通行性,即若到达该点时间大于抢修路段抢修完成时间和到达该点的安全通过概率大于规定值,则道路可通行;反之,舍弃该染色体。
(3)若该需求点的需求量小于车辆载货量,则配送X2中的下一基因位代表的需求点。如果该需求点的需求大于车辆载货量,则该车辆停在该需求点等待下次分配,然后X1中的第二基因位所代表车辆为X2中当前基因位的下一基因位开始配送物资,以此类推。
(4)若所有需求点都有车辆配送后,车辆和救援物资还有剩余,并且还有需求点的需求未被全部满足,则从X1的第一个基因位重复以上过程。
2.3.3 交叉、变异算子
为提高解的多样性和Pareto解集质量,对染色体中的两个字串进行独立交叉,算法中具体采用PMX交叉和优先邻点交叉相结合的混合交叉方式,即能提高种群多样性,又能保证优秀基因片段被保留,提高解的质量。
以9辆车配送9个需求点为例,说明混合交叉过程。从同代种群中随机选择两条染色体A、B。
(1)对X1进行PMX交叉。
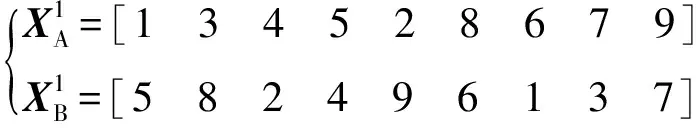
(13)
随机选择两个交叉点,将X1进一步分为三段:

(14)
交换两个交叉点之间的基因段,得到:

(15)
得到交叉片段中的映射关系:2对应4,4对应5,9对应2,通过消除交叉基因段中相同数字得到9对应5,替换交叉基因段之外重复的数字得到新字串:
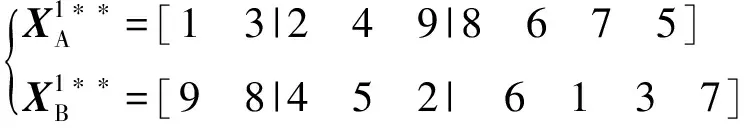
(16)
(2)对X2进行优先邻点交叉。
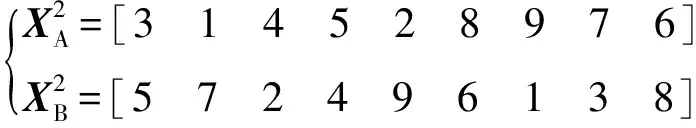
(17)
随机选择两个相邻交叉点a、b,将X2进一步分为三段,将前一位基因记录为ea,后一位基因记录为eb。
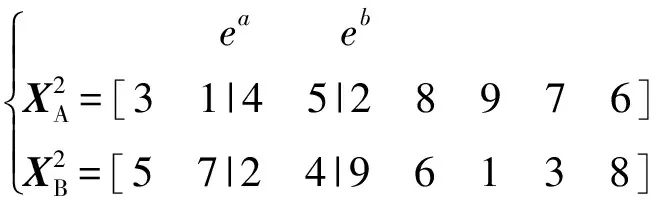
(18)
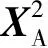
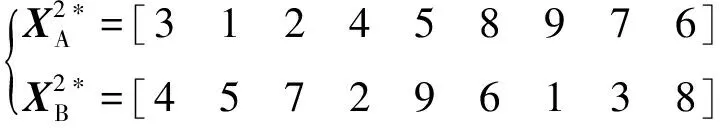
(19)
采用倒置变异的方法进行变异操作。在不同的字串随机生成两点,将两点之间的待变异片段倒置处理得到新的染色体。
2.3.4 快速非支配解排序
所建模型为双目标模型,即车辆最迟服务结束时间和需求点未满足率。假设种群种中有p条染色体,每一条染色体都需要和其他剩下的p-1条染色体就这两个目标进行比较,最终得出Pareto的前沿等级,即非支配解排序。np是在可行解空间中可以支配个体p的所有个体的数量,Sp为可行解空间中所有被个体p支配的个体组成的集合。主要步骤如下:
(1)初始化np=0,Sp=Ø,找到np=0所有的个体,并将它们保存到当前集合Fl中(l为迭代次数)。
(2)对于集合Fl中每个个体k所支配个体集合为Sk,历遍集合Sk中所有个体j,并执行nj=nj-1,若nj=0,将个体j存入另一个集合H。
(3)将Fl作为非支配解集合,并给予集合中的个体相同的非支配序irank,并以集合H作为当前集合,重复以上过程,直到整个种群分级。
2.3.5 确定拥挤度
拥挤度是指种群中给定个体的周围个体的密度,直观上可表示为个体周围仅仅包含自身但并不包含其他个体的最小长方形,用nd表示[11],如图2所示。
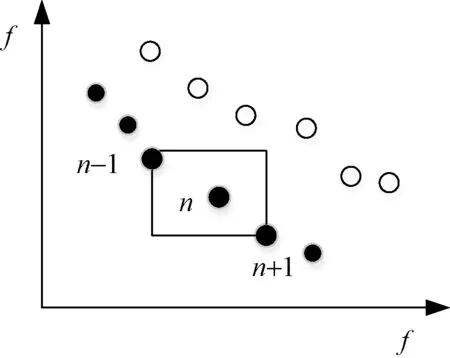
图2 个体n拥挤度Fig.2 Individual n-crowding
种群中每个个体在经历排序和拥挤度计算之后,得到其非支配前沿等级irank和拥挤度nd,定义拥挤度比较算子为≥n,个体优劣的比较依据为
i≥nj,即个体i优于个体j,当且仅当irank
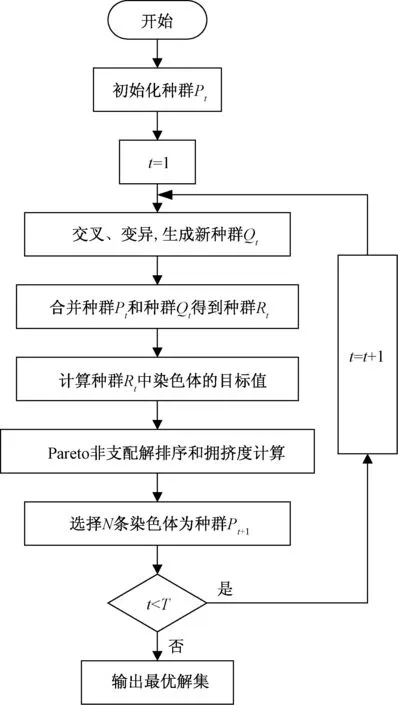
图3 NSGAⅡ 流程图Fig.3 NSGAⅡ flow chart
2.4 NSGAⅡ 步骤
本文采用的NSGAⅡ流程图如图3所示,具体步骤如下:
Stpe1随机生成第一代种群Pt,种群大小为N。
Stpe2对种群Pt进行交叉和变异操作,生成新种群Qt。
Stpe3将种群Pt和种群Qt合并生成新种群Rt。
Stpe4计算种群Rt所有染色体的目标函数值。
Stpe5对种群Rt所有染色体进行非支配解排序和拥挤度计算,得出Pareto前沿等级。
Stpe6通过精英选择策略,筛选出种群大小为N的下一代父种群Pt+1。
Stpe7若当前运行种群代数t>T(T为最大运行种群代数),则输出最优解集;否则t=t+1,并转向Stpe 2。
3 算例分析
参考雅安地震[12]应急资源配送示例,配送中心和需求点的交通网络参数如表1所示。表1中i0表示配送中心,i1,i2,…,i8表示受灾需求点,(a,b,c)表示两相邻节点之间链路的距离 (km)、最大允许行驶速度(km/h)以及道路可靠性(可靠性为0表示道路损坏,待修复;修复完成可靠性为1)。
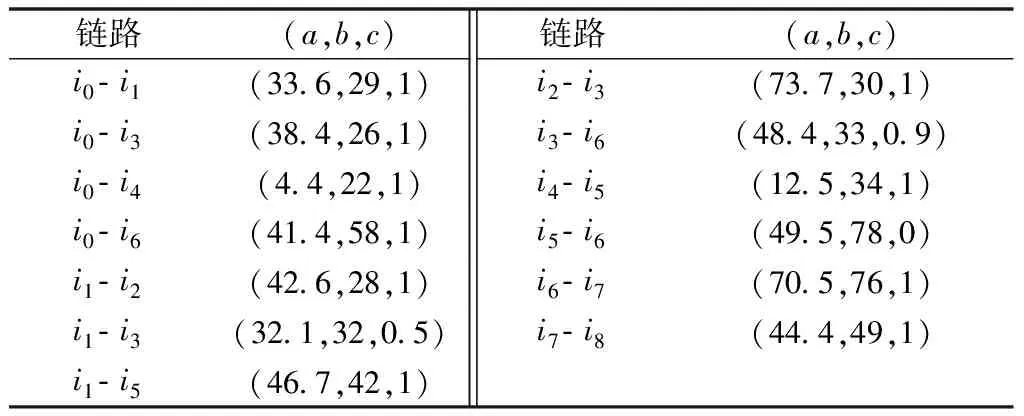
表1 交通网络参数 Table 1 Taffic network parameters
注:道 路i5-i6抢修完成时间tl=1 h。
救援物资配送车辆有大型卡车有6辆,中型卡车4辆和小型卡车6辆,具体车辆类型参数如表2所示。
需求点需求量如表3所示。
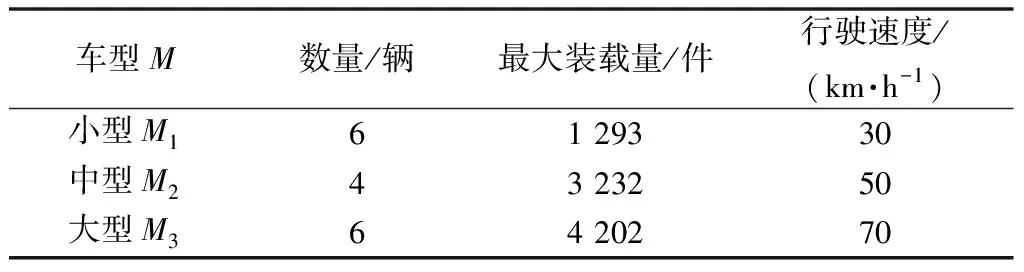
表2 车辆类型参数Table 2 Vehicle type parameters
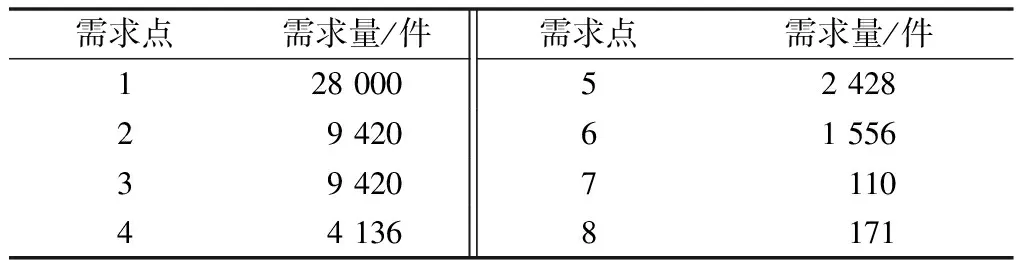
表3 各需求点的应急救援物资需求量Table 3 Demand of emergency relief materials at various demand points
3.1 计算结果
在CPU为Intel(R) 3.3 GHz,内存8 GB的计算机上用MATLAB R2016a对算法进行仿真实验。
算法设置参数如下:种群大小N=100,最大迭代次数T=500,交叉概率Pc=0.8,变异概率Pm=0.5。仿真试验设置以配送时间优先和以配送需求未满足率优先两种方案,得到不同方案下双目标模型的Pareto最优目标值,如表4所示。
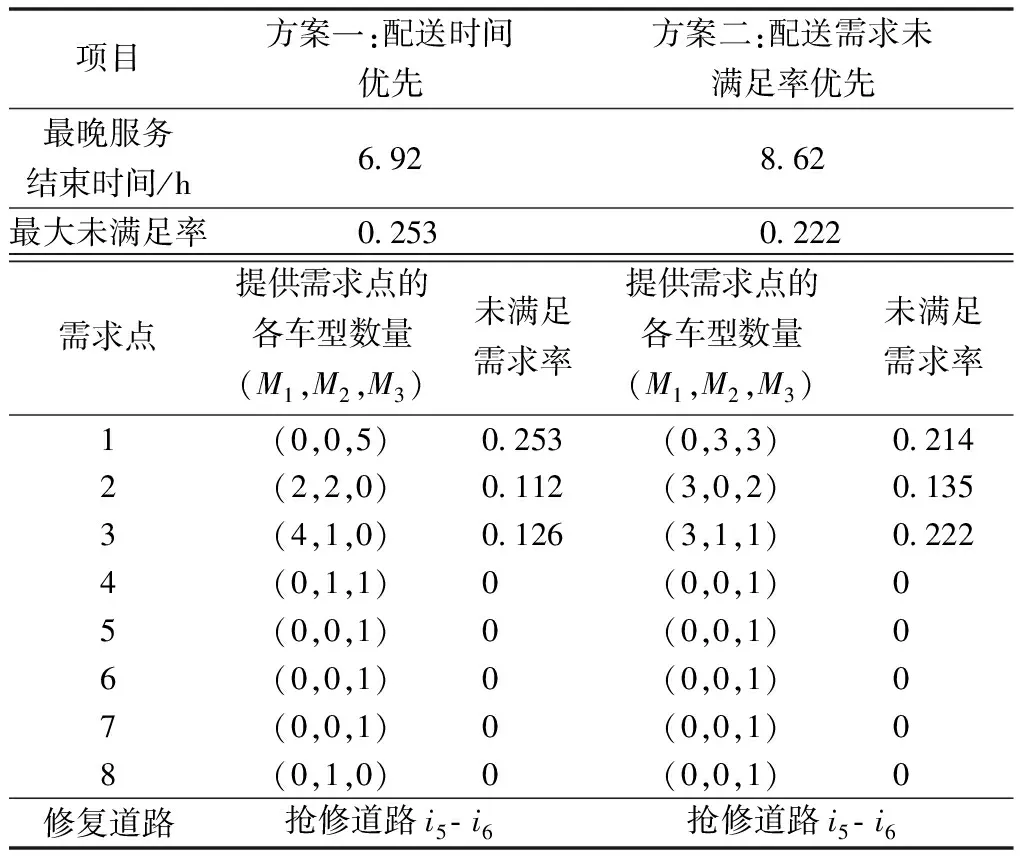
表4 两种方案下双目标 Pareto最优值Table 4 Bi-objiective Pareto optimal solution under two schemes
由表4可知,方案一最晚服务时间为6.92 h,方案二最晚服务时间为8.62 h,相比方案一在配送效率上提高了7.8%。但是,方案一最大未满足率为0.253,方案二最大未满足率为0.222,相比方案一,最大未满足率却下降13%,结果验证了本文所提算法和模型的有效性。
3.2 算法比较
采用基于改进的混合交叉算子NSGAⅡ(简称改进NSGAⅡ)与基于两点交叉PMX算子NSGAⅡ(简称一般NSGAⅡ)两种算法对实例进行仿真实验。得出的Pareto最优解集如图4所示。从图4中可以看出,改进NSGAⅡ对应4个解,一般NSGAⅡ对应3个解,并且前者支配后者,因此改进的NSGAⅡ能够提高局部搜索能力,增加解的多样性。
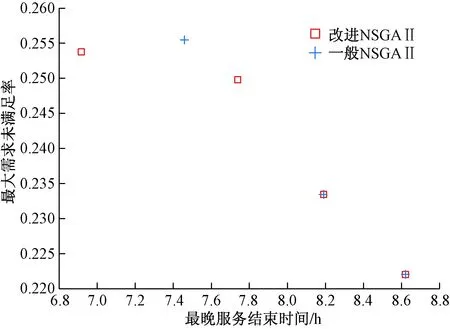
图4 改进NSGAⅡ和一般NSGAⅡ Pareto最优解集Fig.4 Improved NSGAⅡand General NSGAⅡ Pareto optimal solution set
两种算法运行100次之后,得到平均运行时间和最优目标值如表5、表6所示,同时得到两种算法不同目标函数的收敛图,如图5、图6所示。
由表5可知,改进NSGAⅡ的平均时间用时更少,并且两种算法都在5 min内完成,符合现实条件。由表6可知改进算法在时间开销上还能够降低5.9%,配送时间更短。

表5 平均运行时间Table 5 Average running time
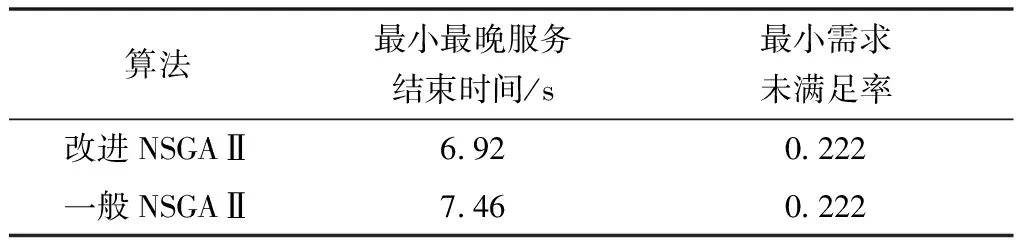
表6 最优值对比 Table 6 Optimal value contrast
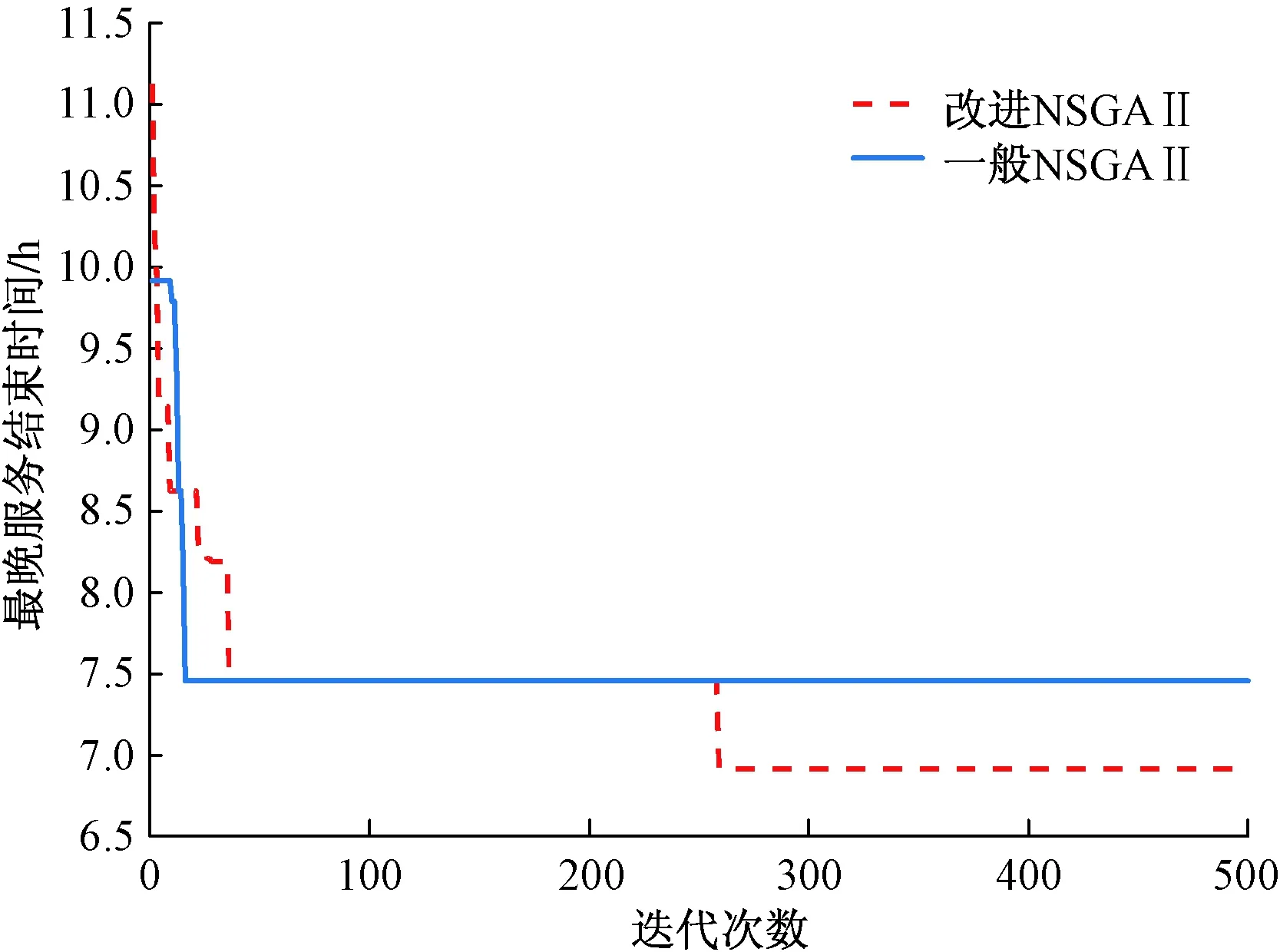
图5 最晚服务结束时间收敛图Fig.5 Convergence graph of latest service end time
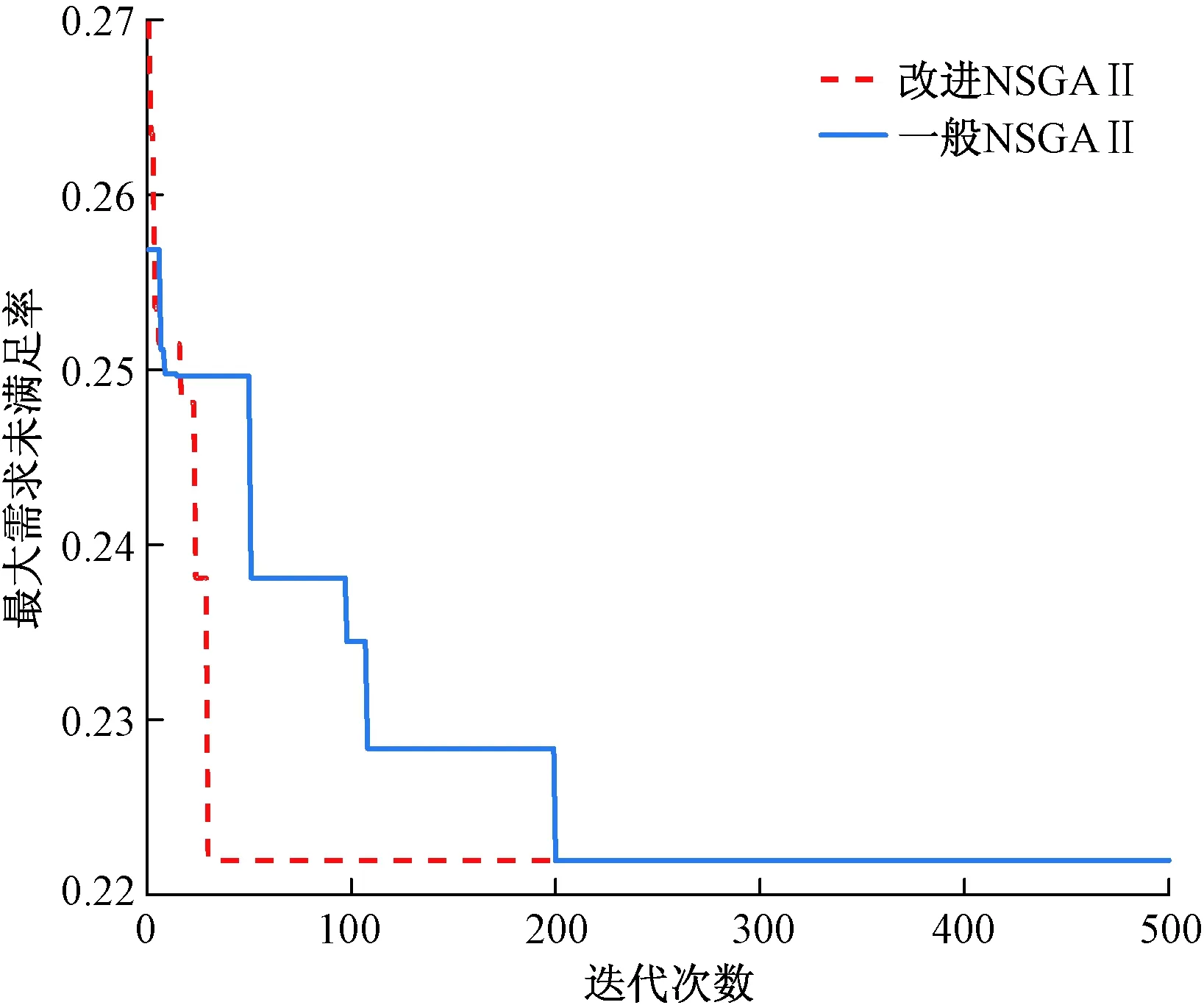
图6 需求未满足率收敛图 Fig.6 Convergence graph of unsatisfactory rate of demand
由图5可知改进NSGA Ⅱ相比一般NSGA Ⅱ,虽然在收敛速度不占优,却能够进一步缩短最晚服务结束时间,提高救援物资配送效率。由图6可知改进NSGA Ⅱ得到的需求未满足率虽然与一般NSGA Ⅱ相同,但是迭代收敛速度更快。实验证明两种算法均有效,改进NSGAⅡ能够提供比一般NSGAⅡ时间更少,选择更多的应急救援物资配送路径。
4 结论
突发事件发生后,选择最优应急救援物资配送路径提高物资配送的效率和效果,是应急决策者面临的主要问题。将最迟服务结束时间和需求未满足率作为目标,考虑实际情况下道路对车型的限制,如道路因受损或道路本身结构如桥梁、窄道等,仅允许某特定类型车辆通过。灾害发生后,部分道路损毁导致路段完全无法通行,需要对部分道路进行抢修,提高配送的效率。灾害发生后,通行路段存在一定的安全风险,在实际情况中需要考虑道路的可靠性。据此建立多目标应急救援物资配送优化模型。设计优先邻点交叉算子对 NSGA-Ⅱ算法提高全局搜索能力和减少运行时间,通过仿真对比试验验证模型和算法的有效性,为决策者选择最优路径提供决策依据。

