计及风力发电的配电网动态无功优化研究
薛培 黄卫华 陈方俊
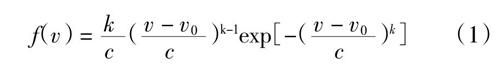

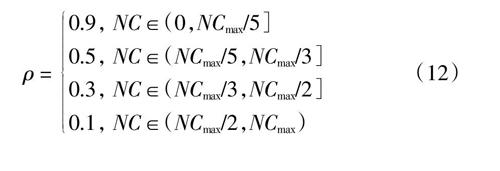
摘 要:风力发电的随机性增加了配电网无功优化的困难程度,在对风力发电随机特征进行分析的基础上,以配电网总有功损耗最小为目标,建立了计及风力发电影响的配电网动态无功优化数学模型,并将改进后的退火蚁群算法应用于该优化模型的求解。建立IEEE33节点配电网系统仿真计算实例,通过与其它优化模型及方法的对比分析验证了本动态优化模型及蚁群求解方法的有效性和优越性。本研究成果可为风力发电在配电网的接入及其无功优化提供有效的技术指导和参考。
关键词:配电网;无功优化;风力发电;退火蚁群算法
中图分类号:TM761 文献标识码:A
Research on Dynamic Reactive Power Optimization
of Distribution Network Considering Wind Power Generation
XUE Pei?覮,HUANG Wei-hua,CHEN Fang-jun
(CGN New Energy Holdings Co.,Ltd,Hefei,Anhui 230000,China)
Abstract:The randomness of wind power generation increases the difficulty of reactive power optimization in distribution network,based on the analysis of the random characteristics of wind power generation,aiming at the minimum total active power loss of the distribution network,the dynamic reactive power optimization mathematical model of distribution network considering the influence of wind power generation is established,the improved anneal ant colony algorithm is applied to the solution of the optimization model. A simulation calculation example of IEEE33 node distribution network system is established,the effectiveness and superiority of the dynamic optimization model and ant colony solving method are verified by comparing with other optimization models and methods. The research results of this paper can provide effective technical guidance and reference for the access of wind power generation in the distribution network and its reactive power optimization.
Key words:distribution network;reactive power optimization;wind power generation;anneal ant colony algorithm
近年来,随着能源危机和人们环保意识的日益加深,新能源的发展越来越得到大家的关注,风力发电以其清洁、环保、安全等优点发展较快,越来越多的风力发电作为分布式电源接入配电网[1]。但风速具有随机性、间歇性等特点,导致风力发电的出力具有不确定性,风力发电在配电网并网后会增加配电网的运行方式优化及无功优化的困难复杂程度,进而影响配电网的经济运行水平及供电质量,风力发电的随机性出力使得传统静态无功优化模型难以有效适应[2],因此研究含风力发电的配电网动态无功优化具有重要的理论和实践价值。
针對含风力发电的配电网动态无功优化,国内外学者进行了相应的研究。文献[3]对国内外风力发电出力预测技术进行了分析,研究了风力发电出力的分布规律。文献[4]对双馈异步风力发电机组的无功调节能力进行了分析,并对其参与含风力发电的配电网无功优化问题进行了一定的分析。文献[5~6]对分布式风力发电并网对配电网的影响进行了研究,并采用遗传算法、粒子群优化算法对配电网进行动态无功优化,表明分布式风力发电会增加配电网无功优化复杂程度,但遗传算法存在着局部搜索能力差、粒子群优化算法存在收敛困难的问题,两种方法均具有易陷入局部最优的缺点。文献[7]采用整体动态无功优化方法来对配电网进行无功优化,但该方法的计算结果具有很大的随机性,稳定性较差,而且直接进行整体动态无功优化会引起维数灾难,导致无功优化的计算量成倍增加,算法收敛困难。以上文献均未对风力发电随机性与负荷变化的影响进行很好地考虑,且配电网动态无功优化存在着优化求解效果不理想的问题。
在对风力发电随机特征进行分析的基础上,以配电网总有功损耗最小为目标,建立了计及风力发电的配电网动态无功优化数学模型,并将改进后的退火蚁群算法应用于该优化模型的求解,通过IEEE33节点配电网系统仿真计算实例验证了本文模型及求解方法的有效性和优越性。
1 风力发电出力特性分析
大量的统计数据分析表明,一个地区的风速规律可以通过Weibull分布[8]来描述,其分布函数表达式为:
f(v) = ■(■)k-1exp[-(■)k] (1)
式中:v表示风速的大小,v0、k、c则分别表示与Weibull分布曲线相关的位置、形状和尺度参数。
风机的有功输出功率Pw与风速v的函数表达式为:
Pw = 0 v≤vci,v≥vcok1v + k2 vci < v < vrPe vr ≤ v < vco (2)
式中:Pe表示风机输出功率的额定值,vci、vr、vco分别表示风机的切入风速、额定风速和切出风速。
将风机的有功输出功率和风速的概率模型相结合,可获得风力发电的概率密度函数表达式为:
f(Pw) = 0 Pw = 0k1v + k2 0 < Pw < PePe Pw = Pe (3)
风力发电机可在恒功率因数控制和恒电压控制两种模式下运行,且均能参与无功功率调节,风力发电机接入配电网后,可以作为配电网的无功控制的无功电源[9]。风力发电机的有功功率Pw与无功功率Qw之间的函数表达式为:
(■)2 + Q2w = (3USIS)2(■)2 + (Qw + 3■)2 = (3■USIr)2 (4)
式中:s表示轉差率,Us、Is、Xs分别表示风力发电机定子侧的电压、绕组电流和漏抗,Xm表示励磁电抗,Ir为表示风力发电机转子侧变流器电流。
风力发电机接入配电网后可作为一种连续无功电源来进行配电网的无功优化控制,从而解决配电网传统无功调压手段调节离散化、调节速度慢等问题,并可有效节省配电网中安装无功补偿装置所花费的费用。
2 配电网动态无功优化数学模型
2.1 目标函数
将经济性目标与安全性目标二者相结合来作为配电网无功优化的目标函数,经济目标为配电网全天总有功功率损耗最小,安全目标为以全天带安全性指标的电压水平最好。优化模型目标函数的表达式为:
minF = ■ft (5)
ft = c1Ploss + c2■αi■(■)2 (6)
式中:ft表示配电网某时段的目标函数值,本文进行配电网动态无功优化时将全天划分为24个时段;Ploss表示配电网总有功损耗;c1、c2分别表示经济性目标和安全性目标的权重系数;N表示配电网所划分的区域数目;αi表示区域i的安全性指标值;Ujs、Uj、Ujmax、Ujmin分别表示节点j的电压标准值、实际电压幅值、电压上限值和电压下限值;li-1+1、li分别表示区域i内的节点数为从li-1+1到li个。
配电网划分区域后各区域的安全性目标函数结构如下图所示:
■
图1 安全性目标函数结构图
2.2 约束条件
对配电网进行动态无功优化需满足的约束条件有等式约束和不等式约束两种,等式约束条件主要是指配电网系统潮流需满足功率平衡的等式约束条件,而不等式约束条件主要是指需满足状态量约束和控制变量约束条件等[10]。
等式约束条件为:
PGi -PDi = Ui■Uj(Gijcosθij + Bijsinθij)QGi +QCi -QDi =Ui■Uj(Gijsinθij+Bijcosθij) (7)
式中:Pi、PGi和PDi分别表示注入节点i的有功功率、风力发电机的有功出力和节点i所消耗的有功负荷大小;Qi、QGi、QCi和QDi分别表示注入节点i的无功功率、风力发电机的无功出力、补偿电容器输出的无功功率和节点i的无功负荷大小。
不等式约束条件中的控制变量约束表达式为:
QDGimin≤QDGi≤QDGimax i = 1,2,…,NGQcjmin≤Qcj≤Qcjmax j = 1,2,…,NCKTKmin≤QTK≤QTKmax K = 1,2,…,Nt (8)
不等式约束条件中的状态变量约束表达式为:
VDi.min≤VDj≤VDj.max j = 1,2,…,ND (9)
式中:QDGimin、QDGimax分别表示风力发电无功出力的下限值和上限值,QCimin、QCimax分别表示无功补偿电容器的无功容量下限值和上限值,KTKmin、KTKmax分别表示有载变压器变比的下限值和上限值,VDjmin、VDjmax分别表示配电网节点电压的下限值和上限值。
2 退火蚁群法原理
模拟退火算法是基于Monte-Carlo迭代求解策略的一种启发式搜索,其全局搜索能力较强但求解的精度偏弱[11]。蚁群算法是一种基于蚂蚁集体觅食过程中群体协作寻找食物源的模拟进化算法,算法具有较高的求解精度,但容易出现停滞及局部最优的现象[12],本文将两种算法进行有效的融合,利用模拟退火算法寻优具有概率突跳性的特点来使蚁群算法跳出局部最优解,从而获得全局最优解,退火蚁群算法的基本流程如图2所示。為提高蚁群算法和模拟退火算法的寻优性能,本文结合相关文献的研究对算法进行相应的改进:将蚁群算法中每次寻优迭代产生的全局最优路径作为信息素的更新[13],改进后的全局信息素更新公式如式(10)和式(11)所示,信息素挥发因子公式如式(12)所示。为避免蚁群算法进入停滞状态,对全局信息素设置上下限,信息素浓度的改进公式如式(13)和式(14)所示。
■
图2 退火蚁群算法基本流程
tij(t + 1) = (1 - ρ)tij(t) + Δtij(t,t + 1) (10)
Δtij(t,t+1)=Q/Lk,if(i,j)位于该蚂蚁的路径上0,if(i,j)不位于该蚂蚁的路径上
(11)
ρ = 0.9, NC∈(0,NCmax/5]0.5, NC∈(NCmax/5,NCmax/3]0.3, NC∈(NCmax/3,NCmax/2]0.1, NC∈(NCmax/2,NCmax) (12)
tij = tij - 10ξtij,m/4 < mij < m/3 (13)
ξ∈(0.01,0.05) (14)
式中:Lk表示算法中每代的最优解,m表示蚁群算法的蚂蚁总数。
对模拟退火算法的改进主要包括[14]:(1)增加记忆功能,记住寻优过程中的最优解,并即时更新,防止丢失全局最优解;(2)模拟退火算法温度下降的幅度随该温度下状态被接受的次数的增加而增大;(3)当模拟退火算法的温度降低到某一值时,逐渐减小扰动的大小,以加快收敛至最优解的速度。
在对配电网动态无功优化的目标函数进行求解时的概率潮流计算采用两点估计法[15],并在进行潮流计算时计及风电场出力随机性的影响。两点估计法的主要思想为:选取一个不确定变量,并在其均值的两侧各取一个值来代替它,而其他不确定变量则取均值。将风电场等效为PQ节点,其有功和无功出力分别由式(2)和(4)计算求得。
4 配电网动态无功优化的实例分析
4.1 系统计算实例
以IEEE-33节点配电网系统作为测试系统对本文模型及方法进行相应的验证,并对其进行相应的改进:在根节点加上有载调压变压器,节点14和30处各安装可投切并联电容器5组和8组,节点33接入一个风力发电场。改进后的IEEE-33节点配电网系统如图3所示。系统参数设置为:电压和功率的基准值分别取12.66 kV、10 MVA,节点0为平衡节点,有载调压变压器的电压调节范围为0.95~1.05 kV,共9个档位,步进量为1.25%,可投切并联电容其的补偿容量分别为100 kVar×5和100 kVar×8,分布式风力发电DG由2台1.5 MW的双馈异步风力发电机组组成。
■
图3 的IEEE-33节点系统图
以某地区的典型日负荷曲线为例,假设各时段内的负荷是保持不变,如图4所示。对典型日负荷曲线下的风速大小进行蒙特卡罗模拟[16],然后根据风速与分布式风力发电机有功出力之间的关系,计算得到的分布式风力发电机单台机组的有功功率日变化曲线如图5所示。
■
时间/h
图4 某地区典型日负荷曲线图
■
时间/h
图5 风力发电机组有功出力曲线图
4.2 动态无功优化结果对比分析
对该IEEE 33节电系统采用无功二次精确矩方法进行相应的无功优化分区,共分为3个区:第1分区包括0~5节点和19~25节点;第2分区包括6~18节点;第3分区包括26~33节点。各区域的安全性指标值分别为α1=1/57.42、α2=1/25.42、α3=1/39.66,区域2的安全水平最差,因此其无功电压控制的更加重要,本文取c1=0.9、c2=0.1。
根据建立的计及风力发电的配电网动态无功优化模型,分别采用遗传算法、粒子群算法、蚁群算法和本文退火蚁群算法对该IEEE-33节点配电网实例进行优化求解,考虑负荷与风电出力在各时段的差异性,动态无功优化后的结果如表1所示,图6为四种算法优化时对应的有功收敛曲
线图。
表1 无功优化结果分析
时间/s
图6 无功优化收敛曲线图
由表1和图6的无功优化结果可知,本文退火蚁群融合算法在四种优化方法中的能获得最好的优化效果,优化后的配电网有功损耗最小(527.76kW),系统平均电压最大(0.9936p.u.),优化后的配电网经济运行程度最好、安全性指标最高,且本文退火蚁群算法收敛特性良好,优化时间较短。本文退火蚁群融合算法虽然比遗传算法收敛时间更长一点,但遗传算法陷入了局部最优解,优化效果很差,优化后的损耗在四种方法中是最大的。
5 结 论
建立了计及风力发电的配电网动态无功优化数学模型,模型中考虑了风力发电出力随机性带来的影响,并提出了一种改进的退火蚁群融合算法,将其应用于配电网动态无功优化模型的优化求解,通过IEEE33节点配电网系统仿真计算实例的对比分析,结果表明遗退火蚁群融合算法能获得最好的优化效果,优化后的配电网有功损耗最小、系统平均电压最大,优化后的配电网经济运行程度最好、安全性指标最高,且本章中的方法优化收敛特性优良,算法优化时间较短。该研究成果可为风力发电在配电网的接入及其无功优化提供有效的技术指导和参考。
参考文献
[1] ZHENG W,WU W,ZHANG B,et al. A fully distributed reactive power optimization and control method for active distribution networks[J]. IEEE Transactions on Smart Grid,2016,7(2):1021—1033.
[2] 张丽英,叶廷路,辛耀中,等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报,2010,30(25):1—9.
[3] 杨茂,马秀达,温道扬,等. 风电功率预测研究综述[J].电测与仪表,2013,50(7):7—10.
[4] 赵晶晶,符杨,李东东. 考虑双馈电机风电场无功调节能力的配电网无功优化[J]. 电力系统自动化,2011,35(11):33—38.
[5] 赵亮,吕剑虹.基于改进遗传算法的风电场多目标无功优化[J].电力自动化设备,2010,30(10):84—88.
[6] 蔡昌春,张建勇. 计及分布式发电的动态无功优化[J]. 电测与仪表,2014,51(6):39—44.
[7] 凌峰,史静. 含风力发电的配电网分时段动态无功优化[J]. 电测与仪表,2014,51(24):16—21.
[8] RODRIGUEZ-AMENEDO J L,ARNALTE S,BURGOS J C. Automatic generation control of a wind farm with variable speed wind turbines[J]. IEEE Transactions on Energy Conversion,2002,17(2):279—284.
[9] SANTOS-MARTIN D,ARNALTES S,AMENEDO J L R. Reactive power capability of doubly fed asynchronous generators[J]. Electric Power System Research,2008,78(11):1837—1840.
[10] CASTRO J R,SAAD M,LEFEBVRE S,et al. Optimal voltage control in distribution network in the presence of DGs[J]. International Journal of Electrical Power & Energy Systems,2016,78:239—247.
[11] BOULEIMEN K,LECOCQ H. A new efficient simulated annealing algorithm for the resource-constrained project scheduling problem and its multiple mode version[J]. European Journal of Operational Research,2003,149(2):268—281.
[12] 段海滨,王道波,朱家强,等. 蚁群算法理论及应用研究的进展[J]. 控制与决策,2004,19(12):1321—1326.
[13] 滕志军,张帆,宋明辉. 电能质量监测系统中基于蚁群的WSN路由算法研究[J]. 电测与仪表,2015,52(11):54—57.
[14] 杨卫波,赵燕伟. 求解TSP问题的改进模拟退火算法[J]. 计算机工程与应用,2010,46(15):34—36.
[15] 吳蓓,张焰,陈闽江. 点估计法在电压稳定性分析中的应用[J]. 中国电机工程学报,2008,28(25):38—43.
[16] 邱生卓,谭兴,钟亚军. 双馈风力发电场对电网暂态无功补偿的研究[J]. 电测与仪表,2013,50(8):58—61.

