基于PASS 理论的幼儿数学问题解决及其策略

黄晓敏

（中国石油大学胜利学院教育与艺术学院 山东东营 257061）

一、PASS 理论的内容概述

PASS 理论是戴斯和纳格利尔里（Das &Naglieri）等人在苏联学者鲁利亚关于大脑机能系统化和信息加工过程的思想上建立起来的。鲁利亚认为任何心理活动都不是孤立的，而是由复杂的机能系统来完成的，并将人脑分为三个相互联系的系统：第一机能系统是动力系统，主要用于维持大脑皮层的觉醒状态，也就是注意；第二机能系统是信息接收、加工和贮存系统，主要是对来自内外的信息进行加工与处理，包括同时性加工和继时性加工；第三机能系统是行为调节系统，主要是通过计划对行为进行调节与控制。

PASS 即“计划（Planning）—注意（Attention）—同时性加工（Simultaneous processing）—继时性加工（Successive processing）”四种认知过程的缩写。这四种认知过程又形成三个认知功能系统：注意—唤醒系统、编码—加工系统和计划系统。这三个认知功能系统既相互联系、共同作用，同时又执行各自的功能。［1］

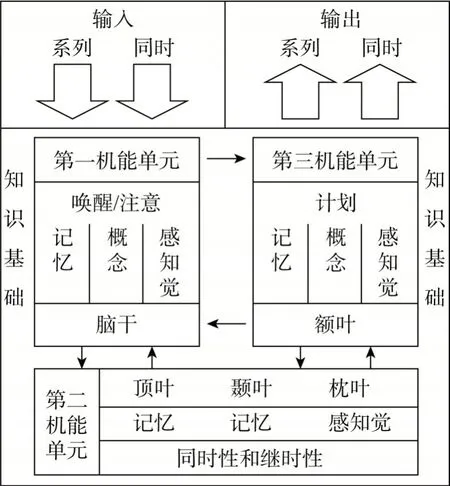
图1 智力的PASS 模型（引自：左志宏，2006）

注意—唤醒系统，对应鲁利亚第一机能单元。该系统是人类心理过程的基础，因为只有在合适的唤醒状态下才能够出现有意注意行为，进而对信息进行加工与处理，过高或过低的唤醒水平都会干扰信息编码。不同于注意，唤醒是大脑皮层的一种警觉状态，而注意属于一种更为复杂的认知活动，在合适的唤醒状态下就会产生选择性注意和分配性注意。选择性注意是对进入感官通道的信息进行选择性加工，忽视无关刺激；分配性注意是将注意分配到不同的活动中或同一时间内注意两种或两种以上的刺激。

编码—加工系统，对应鲁利亚第二机能单元。该系统主要是对新输入的外界信息与已有储存的知识库进行整合、转化、编码，又进一步丰富知识库，包括同时性加工/编码与继时性加工/编码两部分。同时性加工是个体将分散的刺激整合成一个整体或群组，继时性加工则是刺激整合成特定序列从而形成一个链状层级，两者常协同进行。

计划系统，对应的是鲁利亚第三机能单元。该系统主要是对整个认知活动进行计划、检查、协调，是最高层次的认知功能系统。作为人类智力的本质［2］，计划的功能包含了提出新问题，解决问题，对信息的加工编码以及自我监控，并且通过与知识基础更为接近的注意过程、同时性—继时性加工过程，实现对问题解决的方法的选择、应用与评估。这也体现了计划过程不仅依赖而且作用于低级加工过程。

模型各过程之间是相互联系的。首先，第一和第三机能单元之间存在非常密切的关系，因为计划过程的产生和使用需要有适当水平的激活、注意和唤醒作为基础，并且为了实现计划的有效性，需要有选择地抑制或促进唤醒状态，这也是第三机能单元的重要功能。除此之外，从解剖学的角度看，注意—唤醒系统虽直接与定位于脑干的第一机能单元相对应，但定位于额叶的第三机能单元也对注意有着重要的影响作用，原因在于额叶影响有意注意中注意资源的调动。其次，编码—加工系统和计划过程之间也存在紧密联系，因为现实生活中的任务往往可用不同的方式进行编码，计划过程通过选择、调控编码方式的使用直接影响个体对信息的加工，除此之外还受到先前学习经验的影响。三个机能单元是相互联系的，同时又有各自不同的功能，从而保持其独立。编码和计划相互作用，产生各种动作，并促进知识的获得，但高级功能依赖于合适的唤醒水平以提供学习的机会。在这个过程中知识基础作为加工的调节器而发挥作用，知识基础影响各个过程。因此，有效的加工是通过整合知识与计划、注意、同时性加工和继时性加工过程来完成的。［3］

二、PASS理论视野下的幼儿数学问题解决

PASS 理论作为一种认知过程理论，认为人的智力活动包括四个认知过程：计划、注意、同时性加工、继时性加工。在此基础上，幼儿数学问题解决过程是幼儿在已有经验的基础上，明确数学问题的已知状态与目标状态，探索数学问题的解决方法的过程。数学问题解决过程应该是一个认知活动与非认知因素交互作用的过程，而认知活动是数学问题解决的本质和机制。因此，数学问题解决过程作为一种认知活动，同样遵循这四个认知过程。

（一）计划

计划具有指导性和评价性的作用，不仅可以使得认知活动形成一个连贯的整体，保持行为的目标指向性，还可以将评价结果与目标对比、对方法进行修改与对比以及改正结果。计划过程分为三个部分：产生、选择、执行。［4］在幼儿面临数学问题时，首先是对计划的必要性进行评定，如果有必要就在自己努力下或他人帮助下产生计划，如果有多种选择机会就选取最佳计划，并且在计划执行过程中根据实际情况对效果进行监督，调整计划，直至产生最佳方式。计划涉及对整个数学问题解决过程的监控，包括唤醒、运用某些数学事实，自身解题行为的监控，如何运用决策、策略的使用，对结果的评估等。例如基于幼儿思维具有具体形象性，抽象逻辑思维发展水平较低，进行数学运算、解决数学问题时会采用数手指或者借助外物（雪花片、数字棒），帮助他们协调问题中各个部分之间的关系，所以幼儿在进行数学运算的时候选择数手指策略、操作实物策略；在幼儿5—6 岁时随着数群概念和逻辑思维能力的发展，幼儿能够直接选择算式方法解决问题，会采取加减法策略等；或者随着幼儿记忆的发展，幼儿能够基于过去的经验，通过对问题的理解，通过回忆信息直接套用自己学过的知识进行解答，即自动提取策略。［5］

（二）注意

注意是问题产生的基础。注意的产生离不开感知觉的参与，对信息的感知是幼儿意识到问题的关键。视觉系统、听觉系统等是信息输入的“门户”，对进入大脑的信息进行筛选，在已有认知经验与幼儿兴趣的基础上引起幼儿的情绪性体验。因为幼儿作为情绪性动物［6］，所以引起幼儿的情绪性体验更能够让幼儿产生注意偏向。［7］在这个过程中非认知因素的参与是引起幼儿有意注意的重要条件。基于心理资源的有限性，注意实际上是对同时可能的对象或者连续不断的思维中的一种占有，它的本质是意识的聚焦和集中。［8］因此，注意的发生是数学问题解决下一环节出现的基础。幼儿在数学问题解决的过程中，通过对问题信息的感知，判断对问题是否感兴趣，或者自己是否有能力解决，然后将获得的信息转换成自己理解的方式储存，这种状态下，幼儿能够专注于数学问题信息；如果幼儿对问题不感兴趣或者在已有经验的基础上判断自己不能解决，而放弃对数学问题解决办法的探索，主要表现为“走神”，注意力分散，关注周围无关事实。

（三）同时性加工

数学问题解决中的许多技能在很大程度上依赖于同时性加工。［9］同时性加工指的是将个别刺激整合为有机整体，而不是将所有的刺激进行简单的拼凑。

当信息刺激引起幼儿注意时，幼儿则感知到问题的存在，在此基础上幼儿会对问题进行表征，形成对问题的理解。在这个过程中，幼儿首先对新输入的刺激进行字面意义的理解，用自己的话重新表述问题并转化为自己的内部心理表征，这时短时记忆起着重要作用。幼儿在对问题进行初步表征后，从长时记忆中提取相关信息，将相关知识经验与对问题表层理解有机整合，对问题进一步深入理解，包括识别问题类型、区分有关信息与无关信息。［10］这一系列操作的结果就是明确了问题，包括问题的初始状态、目标状态以及各种操作。

幼儿理解问题之后下一步就是解决问题。在这个过程中包含两个过程：选择解决方法和方法应用。选择解决方法的过程也是对问题归类的过程。即使是幼儿的数学问题，也会存在不同的问题模式——数、计算、空间几何、测量等，不同的模式下会有不同的学习内容。例如空间几何中包括图形辨认、图形命名、图形推理等，同一种模式下会有相同或相似的解决方法。幼儿在感知到数学问题，进行心理表征后，对问题进行归类，在自己认知结构中找到与此问题相匹配的数学模式，也就明确了解题方法。如果幼儿能够找到合适的解决方法，就会在原来的解题知识、技巧、记忆等影响下解决问题，否则幼儿可能会寻找其他方法，例如求助教师、父母或同伴。

（四）继时性加工

实际上在认知活动中，同时性加工与继时性加工是同时进行的，既可能是较低层次同时加工的产物，而其结果又可能是下一步更高水平的同时加工的单位。［11］继时性加工是先后依次对几个信息单元进行加工，有利于序列信息的获得、贮存和提取。例如幼儿在学习算式“3+6=9”时，先对问题的表征与模式识别等同时性加工，然后他要把这一信息当作逐次出现的信息流进行学习，即通过死记硬背或数数等来解决问题，最后得出计算结果。这种方式以继时性加工为基础，而且是幼儿在初学算数时最常用的加工方式。［12］

三、PASS 理论视野下幼儿数学问题解决教学存在的问题及其原因

（一）幼儿数学问题解决教学存在的问题

1.教师缺乏对幼儿数学问题解决中元认知的认识

计划在幼儿数学问题解决中具有指导性的作用，能够监督、监控数学问题解决过程，也影响幼儿数学问题解决策略的选择与使用。计划功能的执行是幼儿元认知的重要组成部分，但是在教学指导中教师较少关注幼儿元认知在数学问题解决中的作用。首先是在幼儿数学问题解决中较少通过提问或提醒的方式帮助幼儿思考先做什么，然后做什么，以及提醒幼儿随时观察自己的操作过程是否正确；其次是教师较少关注幼儿在数学问题解决过程中策略的使用，例如较少让幼儿讨论哪种策略最有效；最后是在幼儿数学问题解决中不注重幼儿对操作过程的评价，影响了幼儿对自身的反思，不利于计划在幼儿数学问题解决中发挥积极的作用。

2.教师缺乏有效策略吸引幼儿注意

与故事、绘本等相比，数学问题对幼儿来说缺乏趣味性，所以在幼儿数学学习的过程中需要教师采取恰当的措施吸引幼儿的注意力。但是在幼儿数学问题解决过程中，教师缺乏有效策略影响幼儿对数学问题的注意。首先表现在数学问题趣味性不足，例如教师问题情境的设置缺乏故事性，导致问题难以吸引幼儿注意；其次表现在教师对操作材料运用不恰当，导致幼儿注意力的转移，例如在认识基本的几何图形中，教师提供各种形状的真实的饼干供幼儿观察、比较，但是在实际操作过程中幼儿将饼干含到嘴里，教师提问的时候，幼儿吐出来观察。教师的策略虽然看似吸引幼儿对数学问题的注意力，但实际上将幼儿的注意力转移到了“吃饼干”上。［13］

3.教师数学问题设置非生活化

同时性加工主要是幼儿将问题信息感知并表征的过程。幼儿通过对数学问题的感知获取信息加工的材料，根据感知问题信息和已有的知识经验，而构建问题空间，在头脑中形成具体清晰的形象，形成对数学问题的表征。因为幼儿心理发展的局限性阻碍了幼儿对很多数学问题的感知和表征，所以需要教师的引导，对材料进行加工，帮助幼儿理解数学问题，建构问题空间。但是教师数学问题非生活化设置影响幼儿对问题的感知和表征。首先表现在教师数学问题情境创设不符合生活逻辑，例如在学习按物体的数量分类时，教师设计了“整理超市货架”情境，引发幼儿“按物体数量分类”的思考。教师提问：这么多的物品怎么分类到货架上？幼儿提出了按照物品种类、大小等不同的分类方法，但是教师还是以小动物的口吻提出“要把相同个数的物品放一起”的方法摆放货架。［14］案例中教师的做法不仅不符合幼儿的生活常识，并且影响了幼儿对数学问题的表征。其次还表现在教师问题的设置脱离幼儿实际生活，幼儿知识迁移困难。例如学习“7 以内的序数”中，教师创设7 只小动物春游的故事情境，幼儿通过小动物改变队形（直排、斜排、半圆等）学习不同方向确定物体在序列中的位置，并且幼儿的序数学习一直在虚拟的情境中，并没有和的幼儿实际生活经验相结合，不利于幼儿对问题的表征。

4.教师在数学活动中提供的操作材料不合理

继时性加工是幼儿数学问题解决的过程之一。基于幼儿思维发展的特点，幼儿需要借助操作性材料帮助幼儿进行继时性加工，进而解决数学问题。但是在幼儿数学问题解决过程中教师所提供的操作材料往往不利于问题解决。首先表现在操作材料虽然较为充足，但是存在重复利用性高，多样性、层次性不够，主要来源于幼儿园统一订购的纸质材料，操作方式也单一，主要是通过圈圈画画的方式来验证问题；其次是对材料的操作多为幼儿重复、模仿教师的演示和验证，忽视对数学问题的探索；最后是教师提供的材料难以满足不同认知需要的幼儿，例如图形的拼组与拆分，幼儿水平不同，但是操作材料一样，影响幼儿数学问题解决。［15］

（二）幼儿数学问题解决教学问题的原因分析

1.目标导向的课程评价模式，教师关注目标达成

数学重在培养幼儿的思维能力、问题解决能力，但是现在的课程评价模式主要是以目标导向为主，在这种评价模式下教师在数学课程中更加关注教学目标的达成，关注幼儿数学问题解决的结果，而忽视问题解决的过程，缺乏对幼儿数学问题解决的分析。所以在数学活动中教师关注的是幼儿学到的知识，而不是对于问题的思考过程，例如在数学问题解决过程中缺少引导幼儿自我提问：“我明白这个问题吗？”“是否还有其他方法没有用上？”“我是怎么知道自己每一步算的是正确还是错误？”［16］很多数学课程实际上是知识导向的学习，而未能引发儿童的思考，从而促进儿童思维能力的提高。

2.教师自身数学知识能力的不足

教师自身数学知识能力的不足也是影响幼儿数学问题解决教学的重要原因。教师在数学相关知识缺乏的状况下难以对幼儿数学问题解决过程进行判断，也不能对幼儿的问题解决提供有效指导。研究发现学历较低的教师缺少对数量关系关键经验的内涵、特点的认知，缺少数学教学技能。［17］教师如果对数学教学计划、教学目标、教学过程、教学反思等环节的核心经验不熟悉，那么，他们既不能准确判断自身现有的经验水平，也不能准确判断各类活动中体现的数学核心经验。［18］除此之外，教师对于数学教学反思的不足也是影响教学指导的重要因素，在数学活动结束后教师对教学的反思多停留在目标达成，而对幼儿的参与性、兴趣等关涉幼儿数学问题解决的相关内容较少反思。

3.教师对数学问题解决缺乏重视

2001 年《幼儿园教育指导纲要（试行）》中对幼儿数学教育进行重新定位，数学课程的目标不是知识的学习，而是在生活和游戏中感受事物的数量关系并体验到数学的重要和有趣，学习用简单的数学方法解决生活和游戏中某些简单的问题，学会数学的思维。由此可以看出政策文件对幼儿数学问题解决重要性的肯定，但是也存在另外一个问题，数学知识自身逻辑性强、难度高的特点导致教师课程教学存在诸多困难；数学与科学合并为科学领域，导致数学教育在幼儿园教学实践中常常受到忽视。另外，在数学课程教学中，相对于数学问题解决与数学知识教学相比，知识教学更为简单，在自身能力有限的情况下导致教师更多地选择知识的传授，而不是数学问题解决，所以综合多种原因导致教师对幼儿数学问题解决缺乏重视。

四、提高幼儿数学问题解决能力的教育指导策略

问题解决是人类的一种基本学习活动，幼儿的数学问题解决是幼儿获取数学知识，培养逻辑思维、发散性思维以及创造性的主要途径，但是在日常教育教学中教师不仅要注意到幼儿存在数学问题，也要采取相应的措施，为幼儿创造条件解决问题。

（一）提高幼儿元认知能力，为幼儿计划的使用创造条件

作为元认知的组成部分，计划是个体为解决和达到目标采取的并且不断予以修改的一组决定和策略［19］，计划过程的缺失能导致计算困难［20］。计划在幼儿的数学问题解决过程中实际上起着元认知的作用，所以需要对幼儿进行元认知的培养。在幼儿阶段将元认知融入幼儿园活动，可以有效提高元认知能力。［21］

首先是关于问题解决策略的学习，提升幼儿对策略的认知。卡帕（Kapa）认为儿童有三种基本的问题解决策略，分别是试误（trial and error）、分步规划（step - by - step planning）、整 体 规 划（holistic planning）。［22］通过对不同策略的操作与使用，选择最佳策略。除此之外还需要促进幼儿数学问题解决策略由无策略水平向核心策略水平发展，使得幼儿从具有初步的策略意识，到逐渐能够正确使用策略。［23］

其次是在数学教学活动、小组活动和个别活动中，采用启发式提问、讨论的方法让幼儿注意到对整个问题解决过程的计划、监控等，操作过程中让幼儿在拿到数学问题后先思考打算怎样做，按照计划进行操作，记录过程中遇到的问题以及自己的情绪体验，并在操作结束后运用反思总结的方式让幼儿对自己的操作过程进行评价。教师通过有意识地提高幼儿的元认知能力，培养幼儿在面临数学问题时能够主动控制自己的行为，增强问题解决的计划性、策略性和调控性，进而提升数学问题解决的效率。

（二）创设问题情境，提高教学趣味性，吸引幼儿注意

相对于教学活动，在日常生活中幼儿面临更多的数学问题。在日常生活中应通过问题情境的创设，让幼儿主动发现数学问题。各种有趣的、富含数学教育意义的刺激通过感官吸引幼儿注意，让幼儿发现数学的有趣，在探索中对数学产生各种问题，然后进行独立思考或求助他人解决问题。数学问题情境的创设包括材料的投放、区角活动的设计中注意融入数学中的数、量、形等元素，并且教师要注重运用这些材料，例如在过渡环节中教师带领幼儿认识教室中的数字、图形或者在排队的时候让幼儿自报人数等。

教师不仅要创设数学问题情境，也要在教学活动中提高趣味性，才能吸引幼儿注意，激发幼儿的兴趣和积极情绪，因为与不带情绪色彩的刺激相比，具有情绪含义的刺激更能吸引注意或占用注意资源，引起注意偏向。［24］在数学教学活动中，如果教师因为数学的抽象性，忽视过程中的趣味性，就容易导致教学的失效。因此，在教学导入中可运用更加吸引幼儿注意的声音、图像、玩具等，在过程中采用游戏的方式让幼儿注意力更为集中。例如建立教室地图，让幼儿说出物体的相对位置以及物体之间的距离；通过戏剧或游戏的形式，让幼儿形成对空间词汇（上、下、上方、前方、旁边、中间和右侧等）的理解。

（三）提高自身语言运用能力，注重幼儿已有经验的迁移作用

幼儿在对输入的信息进行同时性加工时，就会对这些信息进行初步理解，形成对问题的表征。幼儿阶段的数学教学信息的呈现方式更多的是口头语言与数字，所以教师的语言运用能力很大程度上影响幼儿的同时性加工，进而影响问题解决。一方面，基于幼儿理解能力有限，所以教师在对幼儿描述数学问题时，应多采用通俗易懂的语言；另一方面，呈现问题以“你”语言（you -language）的形式，也就是将幼儿作为问题情境中的主体更有利于数学问题的解决。［25］教师在创设数学问题情境时注意将幼儿作为主体，能提高幼儿对问题的理解与表征。例如，将“小明有1 个气球，小红给了他3 个，小明一共有多少个气球？”这个问题重新表述成：“你有1 个气球，然后我给了你3 个气球，你现在有多少个气球？”

因为同时性加工过程中涉及幼儿对问题的深层理解，这与幼儿已有知识和经验直接相关，所以教师需要重视幼儿已有经验的迁移作用，将生活经验融入数学教学过程中，深化幼儿对数学问题的理解。例如让幼儿通过感知身高、体重、时间、体温、金钱等，获得比较、标准测量和排序的经验；幼儿学习幼儿园建筑的对称、目测桌椅的长度等内容，习得与实际生活相关的教学知识。

（四）为幼儿提供实物，在操作中解决问题

基于幼儿在数学问题解决中继时性加工的特点，多采用数数的方式，而且数手指和操作实物的策略呈外显性，有助于幼儿解决比较复杂的问题［26］，所以在教学过程中应采用实物教学，让幼儿在操作中整合大脑序列信息，解决数学问题。尤其是低龄幼儿的抽象逻辑思维还处于萌芽阶段，更需要材料的帮助，可利用蒙台梭利的乘法板、除法板帮助幼儿通过数豆豆的方式理解乘法、除法的意义，解决数学运算中的问题。除此之外，教师需要提供多样化的实物操作材料，提高操作材料层次性，开展不同形式的操作活动，提高幼儿操作材料的探索性。

由于三个机能单元是相互联系的，所以教师在幼儿数学问题解决过程中还需要注意幼儿三个机能单元的联系。首先，教师需要具有扎实的数学教学知识和技能技巧，能够唤醒并选择合适的幼儿数学学习状态，抑制无关的干扰因素；其次，教师应鼓励幼儿采用多种方式加工数学问题信息，并引导幼儿对信息加工过程进行自我监控，积极运用评价；最后，教师应重视知识基础的作用，即先前经验。在幼儿的学习过程中，先前经验在幼儿知识建构中发挥着重要作用，也是幼儿意义学习的前提，所以在幼儿数学问题解决过程中，教师应充分利用先前经验的作用，例如幼儿学习“7 的分解组合”，教师可以借助“5 的分解组合”帮助幼儿解决问题。