哑铃型氧间隙缺陷在UO2材料内扩散的分子动力学研究

张华阳，王庆宇，李忠宇

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

二氧化铀(UO2)是核反应堆中最常见的燃料，反应堆运行期间核燃料会受到裂变碎片、气体扩散和热应力应变等效应的影响，造成微观结构的损伤并引起宏观性能的变化，进而影响核反应堆的安全运行。所以，UO2材料的辐照损伤效应研究一直是核燃料研究的重要课题之一。用于研究辐照损伤效应的方法主要有两种，一种是利用离子束辐照实验，能研究材料辐照一定剂量后的微观结构和宏观性能变化，另一种是利用多尺度模拟计算，能研究材料微观结构的连续变化过程。分子动力学方法是多尺度模拟计算中的一种重要方法，能模拟计算nm空间尺度和ps时间尺度内材料微观结构的连续变化，揭示辐照损伤效应的机理。对于UO2材料，其自身的氧原子由于辐照效应，有概率离开原来的平衡位置，在其他位置形成氧间隙原子，氧间隙原子的迁移将影响UO2材料的微观结构以及宏观性能。UO2材料内间隙原子的扩散现象一直是核燃料辐照效应的研究热点。贺新福等[1]曾研究过氦间隙原子的扩散现象，关于氧间隙原子的研究[2-4]主要是在没有应变的条件下研究扩散现象。本文利用分子动力学方法研究应变条件下哑铃型氧间隙缺陷的扩散现象，为实验研究提供理论依据。

1 方法

本文的模拟计算均利用分子动力学软件LAMMPS[5]进行，并结合软件OVITO[6]对模拟计算结果进行分析。LAMMPS是大规模原子分子并行模拟器，能模拟计算百万级的原子或分子系统的微观结构演化，OVITO是一款可视化分析软件，通过读取LAMMPS的计算结果能显示每个原子或分子的运动情况，并能对材料的微观结构进行相关分析。对于UO2材料体系，本文利用Yakub等[7]开发的分数离子模型势函数描述体系中各原子之间的相互作用力，此势函数能精确描述原子间的相互作用以及每个原子的运动情况。

模拟计算需设定UO2材料体系的晶格常数、弛豫温度、拉伸方向、拉伸应变以及时间步长和步数等参数。首先由LAMMPS软件建立UO2材料体系，接着在正则系综(NVT)下进行充分弛豫达到热力学平衡，弛豫温度分别为1 000、1 300、1 500、1 800 K。图1为1 300 K弛豫温度下的UO2体系模型。其中，图1a中z轴方向对应UO2材料体系的〈100〉晶向，尺寸为4.42 nm×4.42 nm×13.27 nm，包含6 144个U原子和12 288个O原子；图1b中z轴方向对应UO2材料体系的〈110〉晶向，尺寸为

图1 达到热力学平衡时UO2材料体系初始模型Fig.1 Initial model of UO2 system under thermodynamic equilibrium

4.42 nm×3.91 nm×9.39 nm，包含3 840个U原子和7 680个O原子；图1c中z轴方向对应UO2材料体系的〈111〉晶向，尺寸为4.06 nm×3.91 nm×11.49 nm，包含4 320个U原子和8 640个O原子。然后在z轴方向上施加拉伸应变，应变比例为1%、2%和3%，UO2泊松比为0.325[8]。最后利用Bai等[9]的方法在体系中间位置添加1个氧间隙原子，在微正则系综(NVE)下，模拟计算整个体系在6 ns内的微观结构变化情况，同时利用Voronoi cell[10]方法判断体系内的间隙原子并跟踪哑铃型氧间隙缺陷质心的运动情况。

结合LAMMPS程序计算得到的哑铃型氧间隙缺陷的质心坐标和爱因斯坦方程[11](式(1))，计算不同温度下哑铃型氧间隙缺陷的扩散系数。 计算时，将模拟计算时间内质心坐标随时间的变化分为K段，每段时间为τK(合理取值范围为20～250 ps[12])。

(1)

其中：D(T)为T温度下的扩散系数；Ri(T)为第i段时间内哑铃型氧间隙缺陷的质心位移；n为哑铃型氧间隙缺陷的扩散维度。计算过程中，在τK的每种取值情况下，选取不同的10个数据起点用于计算D(T)后取平均值，作为该τK对应的扩散系数。绘制τK与D(T)的关系曲线，拟合D(T)值，作为该温度下哑铃型氧间隙缺陷的扩散系数。

2 结果与讨论

2.1 间隙原子排列形态和扩散现象

为研究哑铃型氧间隙缺陷的扩散行为，以z轴方向(对应〈100〉晶轴方向)上3%拉伸应变和无应变两种情况对比，去除正常的原子仅保留间隙原子，观察氧间隙原子的排列情况，结果列于表1。可见，在向体系内添加1个氧原子的情况下，形成了稳定的氧间隙原子缺陷，其中包含2个氧原子，且2个氧原子沿〈111〉方向排列，呈哑铃型，即形成了哑铃型氧间隙缺陷。表1中蓝色为原体系中的氧原子，黄色为添加的1个氧间隙原子，氧原子排布方向构型为添加1个氧间隙原子后进行短暂弛豫，使添加原子后的新体系在预定温度下重新建立热力学平衡后观察到的哑铃型氧间隙缺陷的形态。此时，较低温度(1 000 K和1 300 K)时，添加的氧间隙原子(黄色)在添加位置附近与最近的氧原子(蓝色)形成稳定的氧间隙缺陷；而较高温度(1 500 K和1 800 K)时，在重新建立热力学平衡的过程中，通过碰撞运动，添加的氧间隙原子(黄色)变成正常晶格点位的氧原子，而在新的位置由原本正常点位的氧原子(蓝色)形成新的氧间隙原子，并在其附近与最近的氧原子(蓝色)形成稳定的氧间隙缺陷。

表1 哑铃型氧间隙缺陷排列方向Table 1 Configuration of oxygen dumbbell interstitial defect

图2为1 300 K下沿〈100〉轴向无应变和施加3%拉伸应变时哑铃型氧间隙缺陷的位置。可看出，无应变时哑铃型氧间隙缺陷的运动集中在初始位置附近，扩散运动现象不明显；施加3%拉伸应变时，哑铃型氧间隙缺陷呈现明显的三维扩散现象。

2.2 温度对哑铃型氧间隙缺陷扩散的影响

为研究温度对哑铃型氧间隙缺陷运动的影响，分别将体系弛豫到1 000、1 300、1 500、1 800 K温度，在无应变和〈100〉方向施加3%拉伸应变条件下模拟计算哑铃型氧间隙缺陷的扩散现象。利用爱因斯坦方程计算扩散系数，并绘制扩散系数D和1/kBT的关系曲线，结果如图3所示。由图3可见，模拟计算得到的扩散系数与1/kBT在对数坐标下呈线性关系，与Arrhenius方程描述的一致；随着温度的升高，扩散系数增大，表明在高温情况下由于原子的热运动增强，增大了哑铃型氧间隙缺陷的扩散能力；同时，3%拉伸应变条件下的扩散系数大于无应变情况下的扩散系数，表明拉伸应变能提升哑铃型氧间隙缺陷的扩散能力。

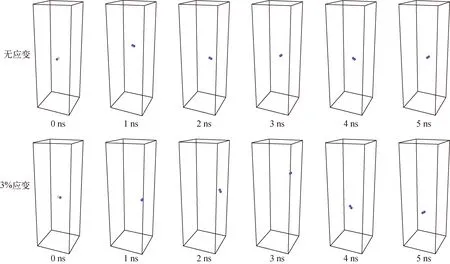
图2 1 300 K下沿〈100〉轴向无应变和施加3%拉伸应变时哑铃型氧间隙缺陷的运动情况对比Fig.2 Comparison of oxygen dumbbell interstitial defect diffusion under 0% strain and 3% strain along 〈100〉 axial with 1 300 K

图3 〈100〉方向拉伸应变下 扩散系数与温度的关系Fig.3 Diffusion coefficient as a function of temperature under tensile strain along 〈100〉 direction

Arrhenius方程表达式如式(2)所示：

D(T)=D0e-Em/kBT

(2)

其中：D0为频率因子，由扩散系数和1/kBT的曲线关系获得；kB为玻尔兹曼常数；Em为扩散激活能。通过计算可得频率因子D0和扩散激活能Em，结果列于表2。

由表2可知，沿〈100〉方向施加3%应变较无应变的频率因子D0更大，这与固体中的扩散理论[13]相符。该理论表明，D0正比于晶格常数的平方，由于对体系施加3%应变，实际原子间距离增大，因此具有更大的频率因子，对哑铃型氧间隙缺陷的扩散运动具有促进作用。利用Arrhenius方程计算出〈100〉方向施加3%应变条件下哑铃型氧间隙缺陷的扩散激活能为0.919 2 eV，无应变条件下为0.876 1 eV。

表2 频率因子D0和扩散激活能Em拟合结果Table 2 Fitting result of frequency factor and migration energy

2.3 应变方向对哑铃型氧间隙缺陷扩散的影响

晶体中原子的排布存在各向异性，所以不同晶向的晶体性质存在各向异性[14-15]，间隙原子沿不同晶向的运动同样存在各向异性[16]。为研究哑铃型氧间隙缺陷沿不同晶向的运动情况，建立了3个体系模型并充分弛豫到1 300 K温度，z轴分别对应UO2材料的〈100〉、〈110〉和〈111〉晶轴方向，模拟计算过程中拉伸应变方向均为z轴方向。分别模拟了无应变和1%、2%、3%拉伸应变条件下UO2中哑铃型氧间隙缺陷的扩散过程，计算了每种情况的扩散系数，结果如图4所示。

图4 1 300 K下哑铃型氧间隙缺陷的扩散系数Fig.4 Diffusion coefficient of oxygen dumbbell interstitial defect with 1 300 K

由图4可见，对应3种拉伸应变方向，扩散系数均随应变的增大而增加，但变化率不同。扩散系数的对数与应变呈线性变化关系，因此可按式(3)对结果进行拟合分析。

D=AeBε

(3)

其中：ε为应变；A、B为待定系数，A表示无应变条件下哑铃型氧间隙缺陷扩散系数，B表示扩散系数随应变变化的显著程度。表3为待定系数A、B的拟合结果。

表3 待定系数A、B拟合结果Table 3 Fitting result of coefficient A and B

由图4和待定系数A可看出，无应变条件下，哑铃型氧间隙缺陷在〈110〉方向的扩散系数最大，在〈111〉方向最小；而在较大应变条件下(3%拉伸应变)，哑铃型氧间隙缺陷在〈111〉方向的扩散系数最大，在〈110〉方向最小。

由图4和待定系数B可看出，拉伸应变条件下，哑铃型氧间隙缺陷在〈111〉方向扩散系数变化最大，在〈110〉方向最小；随着〈111〉方向拉伸应变的相对增加，扩散系数变化得更加明显；随着〈110〉方向拉伸应变的增加，扩散系数变化较为缓慢。所以，〈111〉方向的拉伸应变对哑铃型氧间隙缺陷的扩散影响最大，反之〈110〉方向的拉伸应变对扩散影响最小，不同晶向的拉伸应变对哑铃型氧间隙缺陷的扩散系数影响效果不同，存在各向异性。

2.4 拉伸方向扩散系数的比例

由于哑铃型氧间隙缺陷在UO2体系内的扩散运动呈现三维现象，为研究哑铃型氧间隙缺陷沿拉伸方向的扩散运动趋势，引入参数Dz/D来表示应变方向的扩散系数占总扩散系数的比例，其中Dz表示哑铃型氧间隙缺陷在z轴(应变方向)的分量，利用z方向位移替换爱因斯坦方程中三维均方位移，即可得到Dz。

图5 1 300 K下拉伸方向的Dz/DFig.5 Dz/D along tensile strain direction with 1 300 K

图5为沿〈100〉、〈110〉和〈111〉 3种晶轴方向在无应变和1%、2%、3%拉伸应变条件下UO2中哑铃型氧间隙缺陷沿应变方向的Dz/D。如果三维扩散运动是各向同性的，那么Dz/D将会趋近于0.33。从图5可看出，无论有无拉伸应变，〈100〉方向的Dz/D约为0.5～0.6，大于0.33，这表明哑铃型氧间隙缺陷有明显的沿〈100〉方向扩散的趋势；随着拉伸应变的增加，哑铃型氧间隙缺陷在应变方向的扩散系数比例并没有明显改变。由此可知，虽然增加拉伸应变促进了哑铃型氧间隙缺陷的扩散运动，表现为扩散系数增加，但并未改变拉伸方向的扩散运动比例，且无论有无拉伸应变，〈100〉方向始终是哑铃型氧间隙缺陷的主要扩散方向。

3 结论

本文利用分子动力学方法，研究了沿〈100〉、〈110〉和〈111〉 3种晶轴方向分别施加无应变和1%、2%、3%拉伸应变的条件下，哑铃型氧间隙缺陷在UO2材料体系内的扩散现象。观察到哑铃型氧间隙缺陷的扩散运动是三维的，在扩散过程中始终呈现〈111〉方向排列，且无论有无拉伸应变，〈100〉方向始终是哑铃型氧间隙缺陷的主要扩散方向；研究结果验证了Arrhenius方程对温度和扩散系数之间关系的描述，并发现了应变和扩散系数的指数变化关系。研究发现，温度和应变的增加均会促进哑铃型氧间隙缺陷的扩散运动，且扩散系数随应变变化的显著程度受应变方向的影响，其中〈111〉方向的拉伸应变对哑铃型氧间隙缺陷扩散运动的影响最大；拉伸应变提升了哑铃型氧间隙缺陷的扩散能力，但并未改变其沿拉伸方向扩散运动的比例。关于应变条件下氧原子扩散现象的研究，还需在氧间隙原子的数量和应变方式等方面进行改进补充，将在以后的工作中继续深入研究。