膨胀性土层盾构隧道衬砌管环计算模型
王 寒,邱明明
(1.兰州理工大学土木工程学院,甘肃兰州730050;2.延安大学建筑工程学院,陕西延安716000)
21世纪中国已成为引领世界隧道及地下工程修建技术强国。而盾构法以其施工效率高、质量可靠、技术成熟等优点被广泛应用于城市地铁隧道修建中[1]。盾构隧道衬砌为装配式混凝土结构,其内力与变形计算是混凝土结构设计的关键参数,也是确保衬砌结构服役性能和隧道稳定性的重要指标。由于地下环境的复杂性和区域地质条件的特殊性,使得隧道所受的的外荷载存在较大差异。比如,隧道穿越膨胀土、红黏土、黄土等具有膨胀性[2]的岩土地层,此类岩土体对水分变化十分敏感,其含水率变化会诱发土体产生体积胀缩效应,并引起隧道围岩压力改变,这不可避免的会对隧道衬砌结构内力和变形产生影响。因此,有必要对膨胀性岩土地层盾构隧道衬砌结构内力与变形进行深入研究。
目前,关于考虑膨胀荷载对盾构隧道衬砌结构内力和位移的影响研究相对较少。Lee等[3]推导了考虑接头影响的盾构隧道衬砌管环内力和位移的解析解。林刚等[4]结合成都地铁2号线盾构隧道工程,分析了不同膨胀土分布情况下膨胀荷载分布规律,并采用数值模拟方法探讨了膨胀荷载对衬砌结构内力的影响。方勇等[5]采用现场测试方法分析了膨胀岩土地层条件下盾构隧道衬砌结构的荷载及内力特征。杨军平等[6]通过开展膨胀土隧道物理模型试验,获得了干湿循环作用下膨胀土隧道衬砌内力变化规律。张万志等[7]借助FLAC3D软件分析了降雨入渗条件下膨胀性黄土隧道围岩破坏演化规律。张晟斌等[8]研究了增湿作用下围岩软化与膨胀对膨胀围岩松动压力的影响规律。
本文针对膨胀荷载对衬砌结构内力和位移的影响,通过分析不同膨胀地层分布下隧道膨胀接触压力分布特征,建立考虑膨胀荷载的盾构隧道荷载-结构力学模型,基于结构力学的力法推导不同膨胀荷载模式作用下衬砌管环内力解析解,并结合工程实例进行对比分析。研究成果可为膨胀性地层盾构隧道设计与计算分析提供参考。
1 膨胀围岩荷载分布特征
膨胀性岩土层受大气作用的影响诱发土体含水率变化而产生体积胀缩效应,而土体的胀缩效应必然会引起隧道围压的改变,这对隧道衬砌结构服役性能极为不利。若膨胀性围岩增湿产生膨胀变形压力(隧道径向膨胀力)作用于隧道衬砌结构,可根据盾构隧道穿越膨胀性土层的位置关系,将隧道所受的膨胀荷载分布形式可分为[4,5]:a)隧道顶部分布膨胀性土层,其膨胀荷载作用模式可简化为在隧道顶部呈等腰三角形分布,作用范围与竖向直径夹角为[-π/2,π/2],见图1(a);b)隧道底部分布膨胀性土层,其膨胀荷载作用模式可简化为在隧道底部呈等腰三角形分布,作用范围与竖向直径夹角为[-π/2,π/2],见图1(b);c)隧道两侧分布膨胀性土层,其膨胀荷载作用模式可简化为在隧道两侧均呈倒等腰三角形分布,作用范围与水平方向直径夹角为[-π/4,π/4],见图1(c);d)隧道四周分布膨胀性土层,其膨胀荷载作用模式可简化为在隧道周围均匀分布,荷载作用范围为[-π,π],见图1(d)。
2 计算模型的建立
2.1 荷载-结构模型
以隧道顶部分布膨胀性土层为例,本文建立的隧道荷载-结构模型如图2(ɑ)所示。隧道衬砌管环主要受均布竖向地层压力P1、地基反力P2、均布侧向地层压力P3、三角形分布侧向地层压力P4、管片自重P5、静水压力P6、侧向土体抗力P7和膨胀接触压力P8等荷载作用,运用自由变形圆环法对各荷载作用下盾构隧道衬砌结构内力计算进行推导。计算基本假定如下:a)假设衬砌弯曲刚度均匀,且不考虑接头对管环刚度的影响;b)隧道位于地下水位下方;c)结构计算模型及所受荷载左右对称;d)计算中忽略轴力和剪力对变位的影响。建立的衬砌结构力学计算模型如图2(b)所示。
2.2 力法方程建立
衬砌管环计算模型为三次超静定结构,可根据结构力学中的力法求解其内力。将未知力X1、X2移至衬砌管环的弹性中心(见图2(b)),即柔度系数δ12=δ21=0,则建立的力法方程[9]为
(1)
式中:δii为柔度系数;X1、X2为未知力;Δ1p、Δ2p为在荷载作用下产生的变位。
在单位荷载作用下,基本结构产生的内力为
(2)
若不计轴力和剪力的影响,EI为常数,且ds=Rdφ,则有
(3)
(4)
将公式(4)代入公式(1),可得X1和X2为
(5)
则任意φ角截面处的衬砌结构弯矩和轴力为
(6)
式中:MP、NP为外荷载作用产生的内力。
3 衬砌内力解析解
根据叠加原理,衬砌结构内力可认为是由P1~P8各荷载工况所产生的内力组合,即分别求出各荷载工况下衬砌管环的弯矩和轴力,则可得衬砌管环总内力,如图3所示。其中,P1~P8荷载分布及大小取值参考相关文献或试验确定。
(7)
3.1 荷载P1~P7工况下内力计算
根据图3分别对P1~P7荷载工况下衬砌管环的内力进行计算,具体推导过程如下:
(1)对于均布竖向地层压力P1
(8)
(9)
(2)对于均布地基反力P2
(10)
(11)
(3)对于均布侧向地层压力P3
Mφ,P3=P3R2(0.25-0.5cos2φ),
φ∈[0,π]
(12)
Nφ,P3=P3Rcos2φ,φ∈[0,π]
(13)
(4)对于三角形分布侧向地层压力P4
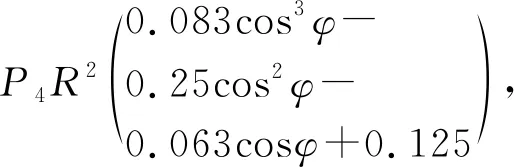
φ∈[0,π]
(14)
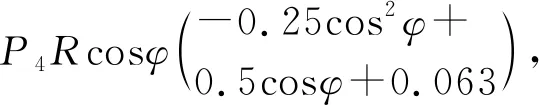
φ∈[0,π]
(15)
(5)对于管片自重P5
Mφ,P5=P5R2(1-0.5cosφ-φsinφ),
φ∈[0,π]
(16)
Nφ,P5=P5R(φsinφ-0.5cosφ),
φ∈[0,π]
(17)
(6)对于静水压力P6
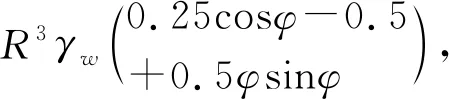
φ∈[0,π]
(18)
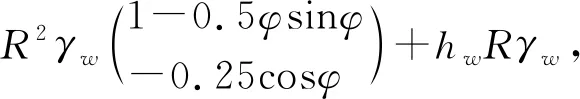
φ∈[0,π]
(19)
(7)对于侧向地层抗力P7
(20)
(21)
3.2 膨胀荷载P8工况下内力计算
考虑盾构隧道穿越膨胀性土层的位置关系,并结合图1分别对P8①、P8②、P8③和P8④四种工况下衬砌管环的内力进行计算,具体推导过程如下:
(1)工况1:隧道上方有膨胀接触压力P8①,其荷载分布呈等腰三角形,作用范围与竖向直径夹角为[-π/2,π/2],则φ截面上的MP和NP为
(22)
(23)
将公式(22)、(23)代入式(5)中,可解出X1、X2。
(24)
将公式(22)、(23)、(24)代入公式(6)可得
(25)
(26)
(2)工况2:隧道下方有膨胀接触压力P8②,其荷载分布呈等腰三角形,作用范围与竖向直径夹角为[-π/2,π/2],则φ截面上的MP和NP为
(27)
(28)
将公式(27)、(28)代入式(5)中,可解出X1和X2。
(29)
将公式(27)、(28)、(29)代入公式(6)可得
(30)
(31)
(3)工况3:隧道两侧均有膨胀接触压力P8③,其荷载分布呈等腰三角形,作用范围与水平方向直径夹角为[-π/4,π/4],则φ截面上的MP和NP为
(32)
(33)
将公式(32)、(33)代入式(5)中,可解出X1、X2。
(34)
将公式(32)、(33)、(34)代入公式(6)可得
(35)
(36)
(4)工况4:隧道四周均匀分布膨胀接触压力P8④,荷载作用范围为[-π,π],则φ截面上的MP和NP为
MP8④=-P8④R2(1-cosφ),φ∈[0,π]
(37)
NP8④=P8④R(1-cosφ),φ∈[0,π]
(38)
将公式(37)、(38)代入式(5)中,可解出X1,X2。
(39)
将公式(37)、(38)、(39)代入公式(6)可得
Mφ,P8④=P8④R2(cosφ-1),φ∈[0,π]
(40)
Nφ,P8④=P8④R(1-cosφ),φ∈[0,π]
(41)
4 算例分析
以某城市地铁区间隧道为例,土质主要为粘性土,隧道覆土厚度H=15 m,管片外直径D=6.00 m,管片计算半径R=2.85 m,管片宽度B=1.00 m,管片厚度t=0.30 m,钢筋砼管片容重rc=25.00 kN/m2,混凝土弹性模量E=3.45×107kN/m3,管片截面惯性矩I=2.25×10-3m4,地下水位HW=20 m,地面附加荷载P0=20 kN/m2,土体重度γ=20 kN/m3,内摩擦角φ=18°,黏聚力c=32 kPa,土的抗力系数K=3.0×104kN/m3,膨胀荷载P8=120 kPa。地下水埋深较深,故不考虑地下水的影响。
如图4所示为膨胀荷载分布模式对衬砌管环内力的影响。如图5所示为各荷载作用下衬砌管环内力分布规律。由图可得,隧道四周有膨胀接触压力时对衬砌内力影响较大,隧道顶部有膨胀接触压力时和隧道两侧有膨胀接触压力时对衬砌内力影响次之,隧道底部有膨胀接触压力时对衬砌内力影响最小;各荷载作用下衬砌管环轴力在拱腰部位较大,弯矩在拱腰、拱底部位较大。
(a)轴力N
(b)弯矩M
图4膨胀荷载分布模式对衬砌管环内力的影响
(a)轴力N
(b)弯矩M
图5不同荷载作用下衬砌管环内力分布规律
5 结论
(1)根据盾构隧道穿越膨胀性土层的位置关系,给出了不同膨胀地层分布下隧道膨胀接触压力简化计算模型。
(2)考虑膨胀性围岩围压改变对衬砌结构内力的影响,建立了考虑膨胀荷载的盾构隧道荷载-结构力学计算模型,推导了各荷载作用下盾构隧道衬砌管环内力解析解,研究成果可为膨胀性地层盾构隧道设计与计算分析提供参考。
(3)结合工程实例分析表明,膨胀荷载对衬砌管环内力影响显著,不同膨胀荷载分布模式作用下衬砌管环内力分布规律存在较大差异。因此,在工程设计应用中,应重视膨胀性地层膨胀荷载对衬砌管环内力的影响,避免因膨胀荷载引起衬砌结构发生灾变。

