关于Pell方程组x2-42y2=1与y2-Dz2=4的
公解高 丽,刘 婷
(延安大学数学与计算机科学学院,陕西延安716000)
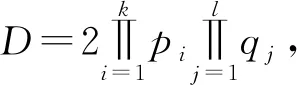
本文主要研究了当D1=42,D为偶数时Pell方程组解的情况,证明下面的定理成立:
定理若p1,…,ps(1≤s≤4)是互异的奇素数,当D=2p1…ps,1≤s≤4时,方程组x2-42y2=1与y2-Dz2=4
(A)
(1)当d=2×337时,方程有非平凡解(x,y,z)
=(±8749,±1350,±52)和平凡解(x,y,z)=(±13,±2,0);
(2)当D≠2×337时,方程仅有平凡解(x,y,z)=(±13,±2,0)。
1 相关引理及证明

引理2[14]当a>1并且a是一平方数,方程ax4-by2=1,x,y∈N最多只有1组解。
引理3[15]如若D是个非平方正整数,此时方程x2-Dy4=1最多只有两组正整数解(x,y),并且方程恰好有2组正整数解的充要条件为D=1785或D=28560或2x0和y0都为平方数,且这里的(x0,y0)是x2-Dy2=1的一个基本解。

引理5 (1)不定方程x4-42y2=1只有整数解
(x,y)=(±1,0);
(2)不定方程169x4-42y2=1只有整数解(x,y)=(±1,±2);
(3)不定方程x2-168y4=1只有整数解(x,y)=(±13,±1),(±1,0)。
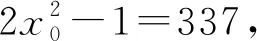
(2)由引理2知,方程169x4-42y2=1最多就一组正整数解,因(1,2)是方程169x4-42y2=1的正整数解,所以方程169x4-42y2=1只有整数解(x,y)=(±1,±2)。
(3)因x2-168y2=1的基本解是(13,1),但是2x0=26是非平方数,y0=1为平方数,由引理3得x2-Dy1仅有一组正整数解,计算知(13,1)是x2-168y4=1的正整数解,故方程x2-168y4=1仅有整数解(x,y)=(±13,±1),(±1,0)。
引理6 假设Pell方程x2-42y2=1的所有解为(xn,yn),n∈Z,任意n∈Z,xn,yn具有下面性质:
(1)xn+1=13xn+84yn,yn+1=2xn+13yn,
yn-1=13yn-2xn,y2n=2xnyn;
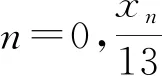
(5)xn+2=26xn+1-xn,x0=1,x1=13,
yn+2=26yn+1-yn,y0=0,y1=2;
(6)xn≡1(mod2),x2n≡±1(mod13),
x2n+1≡0(mod13),y2n≡0(mod4),
y2n-1≡2(mod4),y2n+1≡±2(mod13),
y2n≡0(mod13);
(7)gcd(xn,yn)=1,gcd(xn,xn+1)=1,
gcd(yn,yn+1=2,
gcd(x2n,y2n+1)=gcd(x2n+2,y2n+1)=1,
gcd(x2n+1,y2n)=gcd(x2n+1,y2n+2)=13。
证明Pell方程x2-42y2=1的基本解是
(x1,y1)=(1,3,2),
(1)根据引理4得,∀n∈Z,
故xn+1=13xn+84yn,yn+1=2xn+13yn。
类似可得yn-1=13yn-2xn,y2n=2xnyn。
(2)由条件知,∀n∈Z,
(3)设(xn,yn),n∈Z为Pell方程x2-42y2=1的一个整数解,如果xn=a2,代入该方程得到a4-42y2=1。由引理5(1)得方程a4-42y2=1只有整数解(a,y)=(±1,0),因此xn=1,而n=0。反过来,亦然。

(5)据引理6(1)得xn+2=26xn+1-xn,x0=1,x1=13,yn+2=26yn+1-yn,y0=0,y1=2。
(6)根据引理6(5)可以得出引理6(6)成立。
据引理6(1)(6)得
gcd(xn,xn+1)=gcd(xn,13xn+84yn)=
gcd(xn,84yn)=gcd(xn,yn)=1,
gcd(yn,yn+1)=gcd(yn,2xn+13yn)=
gcd(yn,2xn)=gcd(yn,2xn)=gcd(yn,2)=2,
gcd(x2n,y2n+1)=gcd(x2n,2x2n+13y2n)=
gcd(x2n,13y2n)=gcd(x2n,y2n)=1,
gcd(x2n+2,y2n+1)=gcd(13x2n+1+84y2n+1,y2n+1)=
gcd(13x2n+1,y2n+1=gcd(x2n+1,y2n+1)=1,
gcd(x2n+1,y2n)=gcd(13x2n+84y2n,y2n)=
gcd(13x2n,y2n)=gcd(13,y2n=13,
gcd(x2n+1,y2n+2)=gcd(x2n+1,2x2n+1+13y2n+1)=
gcd(x2n+1,13y2n+1)=gcd(x2n+1,13)=13。
2 定理的证明
证明假设(x1,y1)是Pell方程x2-42y2=1的基本解,这时有(x1,y1)=(13,2)。故而我们根据引理4可以知道Pell方程x2-42y2=1的所有的正整数解为:
设(x,y,z)=(x1,y1,z)是(A)式的正整数解,再从引理6的(2)看到
情形1 当n为正奇数,令n=2m-1,m∈Z+,这时上式可得
从引理6的(1)知,上式即为
Dz2=2xmym·2xm-1ym-1=4xm-1ym-1xmym。
当m=1,代入上式得Dz2=4x0y0x1y1=0,则z只能为0,此时方程组(A)只有平凡解(x,y,z)=(±13,±2,0)。
当m=2,Dz2=4x1y1x2y2=4×13×2×337×5=522×2×337,因此可得z=52,D=2×337,故方程组(A)的正整数解为(x,y,z)=(8749,1350,52),那么方程组(A)的非平凡解为(x,y,z)=(±8749,±1350,±52)。
当m∈Z+,m≠1并且m≠2,需要对m进行分情况讨论:
情形1.1 当m是正偶数且m≠2,根据引理6(7)可得
gcd(xm-1,ym-1)=gcd(xm,ym)=1,
gcd(xm-1,ym)=13,gcd(xm,ym-1)=1,
gcd(xm,xm-1)=1,gcd(ym,ym-1)=2,
这与D的假设矛盾,故此时方程组(A)同样无正整数解。
情形1.2 当m为正奇数且m≠1,根据引理6(7)得
gcd(xm-1,ym-1)=gcd(xm,ym)=1,
gcd(xm-1,ym)=1,gcd(xm,ym-1)=13,
gcd(ym,ym-1)=2,
令m=2k-1,k∈Z+并且k≥2,则有
Dz2=4x2(k-1)y2(k-1)x2k-1y2k-1,
根据引理6(1)知,上式为
Dz2=8x2(k-1)xk-1yk-1x2k-1y2k-1。

情形1.2.1 当k是正奇数且k≠1,令k=2l-1,l∈Z+,定义域为l≥2。将k=2l-1代入上式化简成Dz2=8x4(l-1)x2(l-1)y2(l-1)y2(l-1)x4l-3y4l-3,
再根据引理6(1)得
Dz2=16x4(l-1)x2(l-1)xl-1yl-1x4l-3y4l-3,
取l=2,由上式得
Dz2=16×227137×337×13×2×5896813×
909898=26×132×17×13361×337×453601×
454949。
故可解得
z=104,D=17×13361×337×453601×454949。
此时计算结果与题设条件“D=2p1…ps(1≤s≤4)”矛盾,因此方程组(A)不存在正整数解。
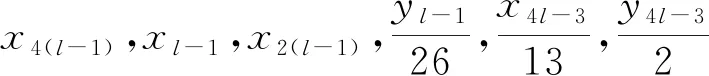
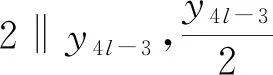

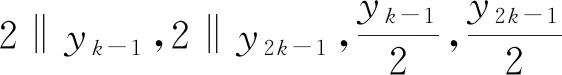
Dz2=8x2(k-1)xk-1yk-1x2k-1y2k-1,
右端是25×132与至少5个互异奇素数的乘积,与题设条件“1≤s≤4”矛盾,故此时方程组(A)依旧无正整数解。


