主题关注网络的表示学习
郭景峰,董 慧*,张庭玮,陈 晓
(1.燕山大学信息科学与工程学院,河北秦皇岛066004;2.河北省计算机虚拟技术与系统集成重点实验室,河北秦皇岛066004;3.河北科技师范学院网络技术中心,河北秦皇岛066004)
0 引言
邻接矩阵作为网络最直观的表现形式,其运算的时间复杂度和存储的空间复杂度均较高,使得很多现有算法无法应用到大规模网络中。针对大规模网络的分析迫切需要一种合理、高效的网络表示方式,因此,网络表示学习成为近年来的研究热点。
网络表示学习[1]与传统的基于邻接矩阵的网络分析方法不同,它结合网络结构和语义等特点学习网络潜在、低维、稠密的嵌入向量空间表示。由于网络嵌入向量很容易被机器学习算法处理,因而受到学术界和产业界的广泛关注,也有效地运用到节点分类、聚类、链接预测等任务中。
社会网络依据包含的节点和边的类型是否相同被划分为两类:同质网络和异质网络。目前,同质网络表示学习方面的方法较多且比较深入;而异质网络表示学习方面的方法大致分为基于矩阵分解的方法[2]、基于自定义损失函数的方法[3-4]和基于神经网络的方法[5-7]三类。其中,基于神经网络的方法[5]中涉及一种基于转移概率模型的随机游走算法和skipgram 模型结合来学习异质网络中节点向量表示的方法。然而,此方法中转移概率模型的定义大多只考虑网络中的基本连接关系(如节点间的直接连接关系),仅仅保持一阶邻近性,无法捕捉全局网络结构。针对上述问题,本文主要基于异质网络的子网络——主题关注网络[8-10]进行表示学习的相关研究。如图1 所示,该网络由两类节点和边构成,其中,ui和tk分别表示用户和主题节点。针对异质网络中节点和边之间结构和语义等各方面的特点,运用集对分析理论中的同异反(确定与不确定)思想,提出了基于主题关注网络的表示学习(Topic-Attention Network Embedding,TANE)算法。主要内容如下:
1)提出一种基于集对分析理论构建转移概率模型的方法。该模型针对主题关注网络中4 阶[11]范围内两类节点(用户和主题)间连接关系中的几种情况,采用集对分析理论中同异反思想将主题关注网络刻画为一个同异反(确定与不确定)系统,构建节点间的转移概率模型。
2)提出一种基于用户和主题节点的游走(User Topicwalk,UT-walk)算法。该算法基于用户到用户、用户与主题之间的转移概率给出随机游走策略,实现两类节点间灵活的游走,得到游走序列,并通过训练该序列得到高质量的网络嵌入向量空间表示。
3)在两个数据集上对本文提出的算法进行了实验,利用K-means++聚类算法进行社区发现,选取模块度作为评价指标,实验结果验证了本文算法的有效性,聚类结果计算出的模块度相对较高。
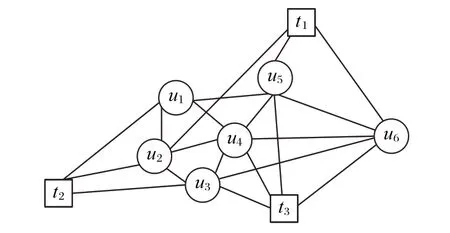
图1 主题关注网络Fig.1 Topic-attention network
1 相关工作
随着社交网络用户的迅速增长使得传统的网络表示方法遇到瓶颈,结合深度学习的网络表示方法逐渐兴起。
DeepWalk 算法[12]首次将深度学习中的技术引入到同质网络表示学习中,该算法运用Word2vec[13]模型的思想将节点视为单词、随机游走序列视为句子,训练得到网络的嵌入向量空间表示,在多标签分类任务上证明了其有效性。Node2vec算法[14]结合广度优先遍历(Breadth First Search,BFS)和深度优先遍历(Depth First Search,DFS)搜索算法,同时考虑到局部和全局信息,改善了DeepWalk 算法中的随机游走策略;LINE(Large-scale Information Network Embedding)算法[15]通过不直接相连的两个节点的邻居刻画二阶相似度,对Deepwalk的一阶近邻稀疏问题作了改进。Node2vec 和LINE 这两个算法较Deepwalk 算法在多标签分类任务方面的结果明显提高。保持Motif 结构的网络表示学习(Motif-Preserving Network Embedding,MPNE)算法[16]结合Motif 结构进行高阶的网络表示学习,在多标签分类任务上取得了更好的结果。SDNE(Structural Deep Network Embedding)算法[17]结合神经网络模型来捕捉网络中高度非线性的关系,最终将隐层权重作为网络的嵌入表示,在链接预测任务上得到了突出的实验结果。
异质网络表示学习研究从PTE(Predictive Text Embedding)[3]算法逐渐起步,该算法是将predictive 的信息在最后的embedding 体现出来,但不像卷积神经网络(Convolutional Neural Network,CNN)或 循 环 神 经 网 络(Recurrent Neural Network,RNN)模型直接嵌套一个复杂的预测模型;PME(Projected Metric Embedding)算法[4]使用度量学习方法同时捕捉网络中的一阶和二阶关系,在对象、关系空间分别学习节点、关系的向量表示;metapath2vec 和metapath2vec++算法[5]均基于DeepWalk 的思想,利用元路径指导随机游走,并用异质的skip-gram 模型进行训练得到网络的嵌入向量空间表示;HIN2vec 算法[6]结合神经网络模型,在得到网络的嵌入向量空间表示的同时还学到了关系(元路径)的表示;DVNE(Deep Variational Network Embedding)算法[7]利用神经网络模型结合Wasserstein距离改变了度量两个分布之间相似性的方法,使其既能满足三角不等式,又能在无向图中很好地保持邻近性的传递性。以上算法在多标签分类、聚类和链接预测等网络分析任务方面取得了较好的实验效果。目前,在基于元路径[18]随机游走策略的异质网络表示学习中带偏置的随机游走方式限制条件较多,因此,有必要针对异质网络表示学习探究新的理论和方法。
2 主题关注网络
主题关注网络[10]被定义为一个二元组G=(V,E),其中:V={U,T},U={u1,u2,…,un}表示用户节点集,T={t1,t2,…,tm}表 示 主 题 节 点 集;E={EUU,EUT}表 示 边 集,其 中,EUU={(ui,uj)|ui,uj∈U}表示用户与用户间的关系,EUT={(ui,tk)|ui∈U,tk∈T}表示用户与主题间的关系。
在主题关注网络中,N(ui)1=NU(ui)1∪NT(ui)1和N(ui)2=NU(ui)2∪NT(ui)2分别表示节点ui的1 级和2 级邻居集(包含用户邻居集NU(ui)m和主题邻居集NT(ui)m,m=1,2);CN(ui,uj)1=CNU(ui,uj)1∪CNT(ui,uj)1和CN(ui,uj)2=分 别 表 示 N(ui)1∩N(uj)1和N(ui)2∩N(uj)2;和CN(ui,uj)2∩1=CNU(ui,uj)2∩1∪CNT(ui,uj)2∩1分 别 表 示N(ui)1∩N(uj)2和N(ui)2∩N(uj)1,其他相关定义详见文献[10]。该网络是融合了社交关系和兴趣爱好的模型,节点之间的边具有明显的语义特征。
3 基于主题关注网络的表示学习算法
3.1 基于集对分析理论的主题关注网络建模
集对分析理论[19]的核心思想是将事物之间的联系看成是一个系统,简称为同异反(确定与不确定)系统。其中,确定性包含同和反,通常指事物的同一和对立两个方面,在此仅考虑同一方面;不确定性为异,通常指事物宏观和微观方面的影响因素。采用该思想构建主题关注网络模型的关键即为构建节点间的确定和不确定关系。
主题关注网络包含用户和主题两类节点,以及用户-用户、用户-主题、主题-用户三种节点间关系,基于该网络的拓扑结构,将两个用户节点通过与其直接相连的节点建立的关系视为确定关系,如用户间如果拥有共同的朋友或兴趣爱好更容易成为朋友;将两个用户节点通过与其间接相连的节点建立的关系视为不确定性关系,如用户间分别通过其朋友分享共同的兴趣爱好成为朋友的不确定性较大,但在一定条件下可转化为确定性关系。如图2 所示,将(ui,uj)、(ui,tk)、(tk,ui)三种节点间二阶范围内的连接关系作为确定部分,其他情况作为不确定部分建模。
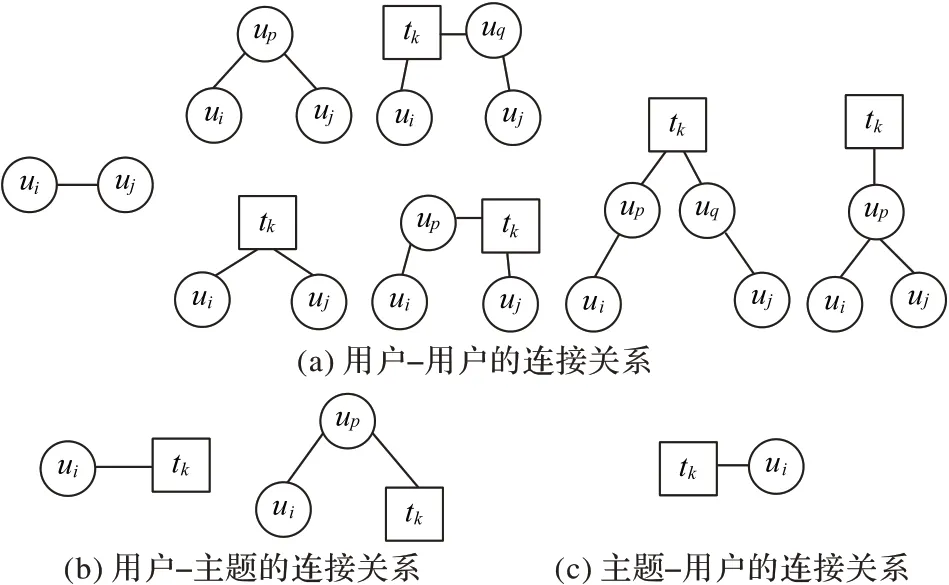
图2 建模涉及的节点间连接情况Fig.2 Connections between nodes involved in modeling
3.2 转移概率模型
3.2.1 相关定义
传统同质社会网络中基于转移概率模型进行网络分析已经结合BFS 和DFS 等方法考虑到节点2 阶范围内的邻居,但无法准确捕捉全局网络结构。基于现实网络的多样性(如网络中包括多种类型的节点和边)及网络关系的复杂性(如朋友间通过共同的兴趣爱好建立联系)在主题关注网络中全面准确地定义转移概率模型作为研究重点。
针对图2 主题关注网络中两类节点间的关系,融合网络结构、主题偏好及确定与不确定性思想构建转移概率模型,具体定义如下。
定义1用户到用户的转移概率。给定主题关注网络G=(V,E),∀ui,uj∈U,tk∈T,考 虑 NU(ui)1、CN(ui,uj)1、CNT(ui,uj)1∩2和CNT(ui,uj)2∩1以及CNT(ui,uj)2,用户到用户的转移概率记为P(uj|ui),如式(1)所示。
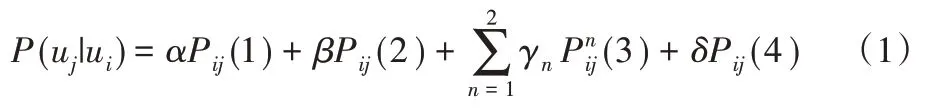
其中:Pij(1)表示两个用户节点是否直接相连,如式(2)所示。

其中:di表示节点ui的度;S起标记作用,S=1表示两个节点间有直接连接关系,否则S=0。
Pij(2)表示两个用户节点通过共同1 级邻居建立连接关系,如式(3)所示。
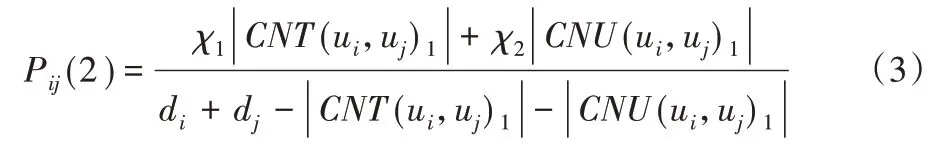
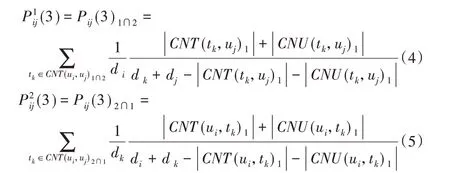
Pij(4)表示两个用户节点通过共同的2 级主题建立连接关系,如式(6)所示;
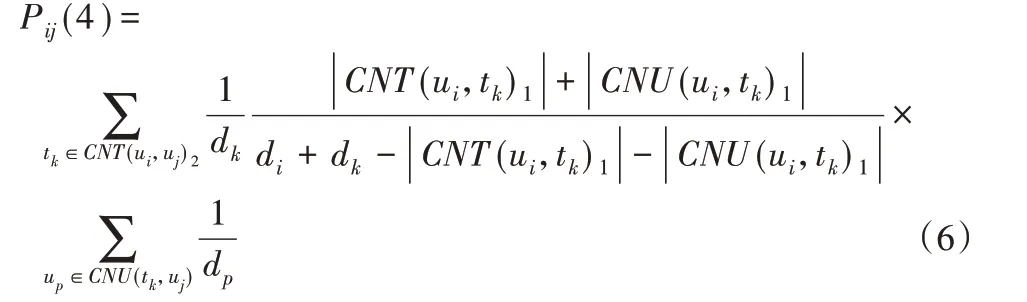
其 中:α、β、γ1、γ2和δ 分 别 表 示CNT(ui,uj)1∩2和CNT(ui,uj)2∩1以及CNT(ui,uj)2所占的权重系数,且α+β+γ1+γ2+δ=1;χ1和χ2分别表示两个用户节点通过CN(ui,uj)1建立连接关系时,两个节点共同的用户和主题所占的权重系数,且χ1+χ2=1。
定义2用户到主题的转移概率。给定主题关注网络G=(V,E),∀ui,up∈U,tk∈T,考虑NT(ui)1、CNU(ui,tk)1,用户到主题的转移概率记为P(tk|ui),如式(7)所示。

其中:Pik(1)表示用户节点和主题节点是否直接相连,计算方法同式(2);Pik(2)表示用户节点与主题节点通过CNU(ui,tk)1建立连接关系,计算方法同式(3);ε、θ 分别表示NT(ui)1和CNU(ui,tk)1所占的权重系数,且ε+θ=1。
定义3主题到用户的转移概率。给定主题关注网络G=(V,E),∀ui,uj∈U,tk∈T,考虑NU(tk)1,主题到用户的转移概率记为P(ui|tk),如式(8)所示。

其中:Pki(1)表示主题节点和用户节点是否直接相连,计算方法同式(2)。
3.2.2 实例
为了更加直观地理解上述定义,利用图1 中的(u1,u4)、(u5,t3)、(t3,u5)分别给出上述定义的计算过程。以节点u1、u4为研究对象,NT(u1)1={t2},NU(u1)1={u2,u4,u5},NT(u4)1={t3},NU(u4)1={u1,u2,u3,u5,u6}。(u1,u4)∈EUU,即S=1;CNT(u1,u4)1=,即|CNT(u1,u4)1|=0,CNU(u1,u4)1={u2,u5},即|CNU(u1,u4)1|=2;同理,节点u1和u4的其他邻居集分别为CNT(u1,u4)1∩2={t2}、CNT(u1,u4)2∩1={t3}和CNT(u1,u4)2={t1},即 |CNT(u1,u4)1∩2|=1、|CNT(u1,u4)2∩1|=1 和|CNT(u1,u4)2|=1。因 此,节 点u1到u4的 转 移 概 率 为同 理 可 得(u5,t3)和(t3,u5)的邻居情况,如表1 所示,计算转移概率分别为
3.3 TANE算法框架
TANE 算法的核心思想是将上述定义得到的转移概率模型运用到随机游走算法得到随机游走序列,通过训练该序列,得到两类节点的向量表示。根据不同的需求利用两类节点的向量表示,如运用网络中用户节点的向量表示进行社区发现任务,或是根据网络中主题节点的分布情况对社区内用户进行合理化推荐等。
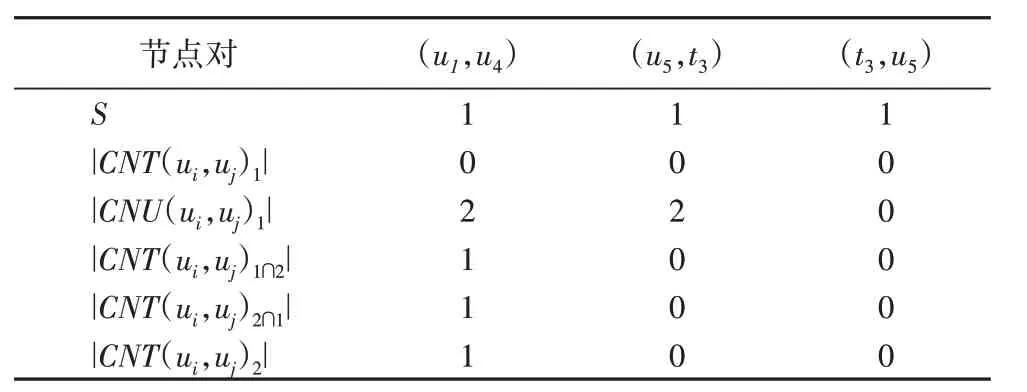
表1 节点对间的邻居数量Tab.1 Number of neighbors between node pairs
3.3.1 UT-walk算法
基于上述三种转移概率模型,提出了基于主题关注网络的随机游走算法,如算法1 所示。在算法1 中,第1)行表示初始化随机游走路径;第2)行表示起始节点的选取是随机的,可为用户或主题节点;第3)~5)行分别表示在游走路径长度L范围内对当前节点(vcurrent)的选取、计算给定vcurrent的前提下转移到下一个节点的转移概率以及下一个节点的选取方法。
在主题关注网络中,结合转移概率模型选取下一个节点主要有两种策略:1)若vcurrent是用户节点,则vnext是用户或主题节点;2)若vcurrent是主题节点,则vnext一定为用户节点。vnext的选取通过带权重(即转移概率)的非均匀采样实现,更倾向于转移概率大(与vcurrent共同用户和主题数量多)的节点。
算法1 UT-walk。
输入 G=(V,E),随机给定一个起始节点u,路径长度L,转移概率P;
输出 包含两类节点的随机游走序列。

以图1 中u1和t3为例说明上述算法,转移概率模型的参数设置与表7中Karate 一致,与其他节点的转移概率如表2所示。由表2可知,如果以u1作为当前节点vcurrent,则下一个节点vnext的选取更倾向于u2、u4、t1、t2转移概率相对较大的节点。由P(u5∣u1)<P(u6∣u1)看出,节点间转移概率大不是因为节点间存在直接连接关系,还有可能是间接连接关系丰富。综上,随机游走下一个节点vnext的选取要考虑节点的间接连接关系。

表2 分别以节点u1和t3作为vcurrent的转移概率Tab.2 Transition probability with node u1 and t3 as vcurrent
3.3.2 TANE算法
主题关注网络表示学习(TANE)算法结合了转移概率模型和UT-walk 算法,如算法2 所示。在算法2 中,第1)行表示初始化随机游走路径集合;第2)~8)行分别表示在每个节点作为起始节点次数n 的前提下,通过UT-walk 算法对起始节点、游走路径长度等参数进行设置,运用转移概率模型得到多条相对高质量的随机游走序列;第9)行使用Word2vec模型对随机游走序列进行训练,得到主题关注网络的嵌入向量空间Φ。
算法2 TANE。
输入 G=(V,E),上下文窗口大小w,每个节点作为起始节点的次数n,生成的向量空间维度d,路径长度L,转移概率P;
输出 节点的向量空间表示矩阵Φ ∈R∣V∣×d。

4 实验与结果分析
4.1 实验设置
4.1.1 数据集和对比实验
实验选取了两个基准数据集和五个经典算法,具体介绍如下。
1)Zachary’s Karate club数据集是社交网络分析领域中的经典数据集,由34个节点和78条边组成。
2)豆瓣数据集是一个通过爬虫程序抓取的包含用户间的关注属性和电影评论属性两部分信息的网络。对数据集进行处理,过滤掉用户对电影评分在3 分以下的信息,最终网络中有2 289 个节点(2 253 个用户+36 个主题)和70 489 条边(34 580 条用户与用户之间的边+35 909 条用户与主题之间的边)。
5 个经典算法分别为:DeepWalk、Node2vec、MPNE、PTE和metapath2vec。为了使实验结果更有说服力,对比算法中的参数均与原论文一致,维度设置如表3所示。
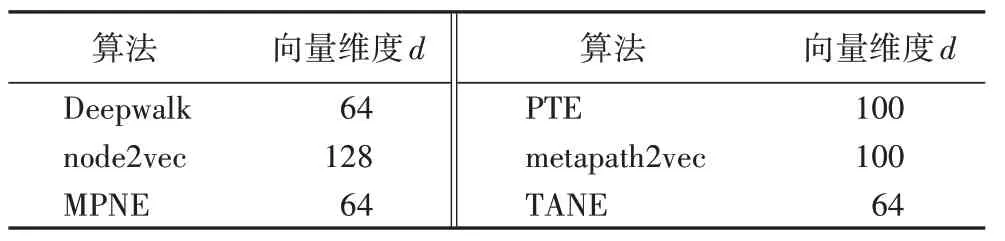
表3 各算法的向量维度设置Tab.3 Vector dimension settings of different algorithms
4.1.2 评价指标
实验选择节点聚类作为网络分析任务,选取模块度(Modularity,Q)作为评价指标,如式(9)所示,Q ∈[-1/2,1),Q越大,则表明社区划分质量越好。
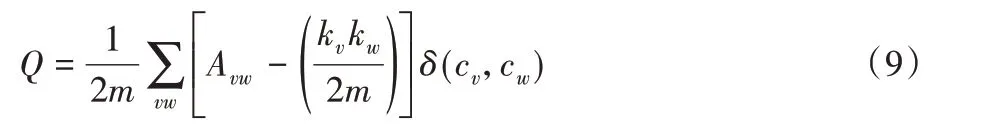
需要说明的是,该实验是为了证明主题节点对社交关系稳定的重要性,主题仅起桥梁的作用,聚类分析以及计算Q时去掉网络中的主题节点。
4.2 结果与分析
实验主要分为三部分:1)验证主题对转移概率和向量表示的影响;2)验证TANE 算法的正确性和合理性;3)参数敏感性分析。
4.2.1 基于Karate网络的实验
Karate 网络是一个无主题的真实网络,针对该网络(如图3(a)所示)及对其添加主题(如图3(b)所示)两种情况进行比较,以分析主题对网络表示学习的影响。
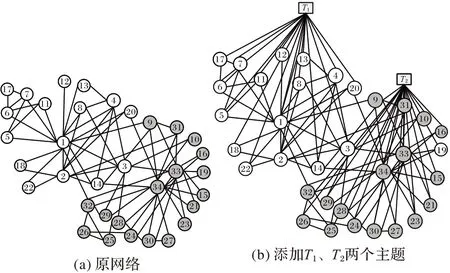
图3 Karate网络示意图Fig.3 Schematic diagram of Karate network
运用DeepWalk算法和TANE算法得到Karate网络的两种嵌入向量空间表示,通过计算节点间向量表示的欧氏距离展开分析。由于考虑4阶范围内节点间的关系,Karate网络较稠密,4阶邻居仅仅涉及1个节点,因此,图4(a)、(b)、(c)分别展示两个算法下34 个节点与每个节点一阶、二阶和三阶邻居间向量表示的欧氏距离变化趋势。
从图4 中可以看出,三种情况下欧氏距离变化趋势基本一致。由于转移概率模型定义时考虑的范围不同,使得Karate 网络中整体节点间向量表示的欧氏距离减小了,有些节点间向量表示的距离的波动情况相比DeepWalk 算法产生了偏差。为了分析产生偏差的原因,以一阶邻居较多的u1、u34节点和容易出现分歧的u3、u10节点为例,将图中部分区域放大,如图5所示。vnext的选取通过带权重(即转移概率)的非均匀采样实现,节点间转移概率越接近,得到节点的向量表示越相似,节点间向量表示的距离越小,图中折线的波动情况反映了此现象。图5 中用加粗线标记波动比较明显的情况,以图5(a)中加粗线标记为例详细分析原因。TANE算法中,u1到标记范围内节点的转移概率如表4 所示,从表中可以看出,P(u1∣u10)最小,其他情况的转移概率相差不大,从而dist(u1,u10)最大,即u10与x轴间的垂直距离最大,所以,虚线标记的折线段除u10处波动明显外其余节点相对平稳;而DeepWalk 算法中,转移概率模型定义仅考虑了一阶邻居,无法根据转移概率对间接连接关系进行详细分析。综上分析,TANE 算法符合网络表示学习的核心思想。
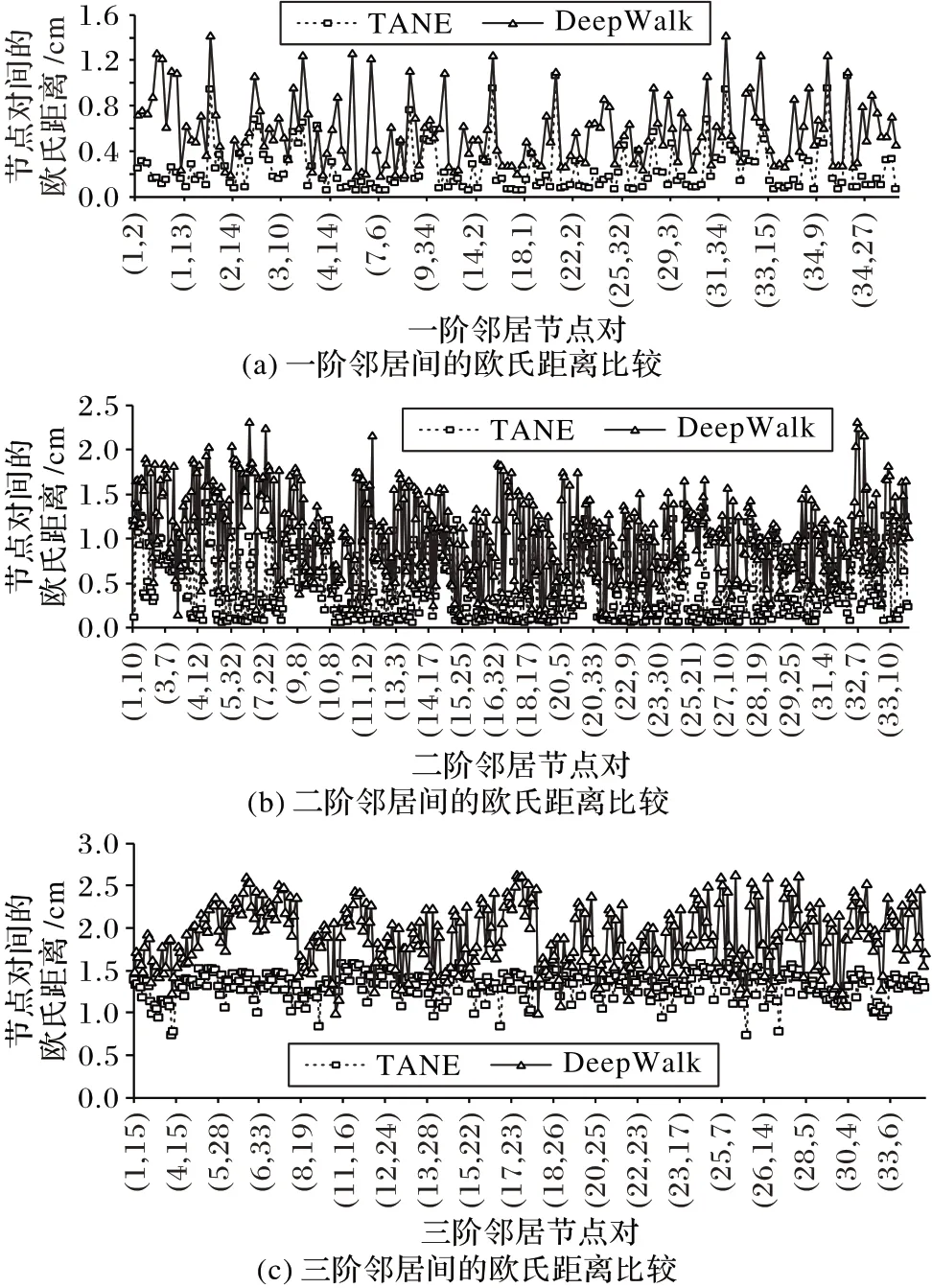
图4 在两种算法下各阶邻居间欧氏距离的比较Fig.4 Comparison of Euclidean distance between neighbors in two algorithms
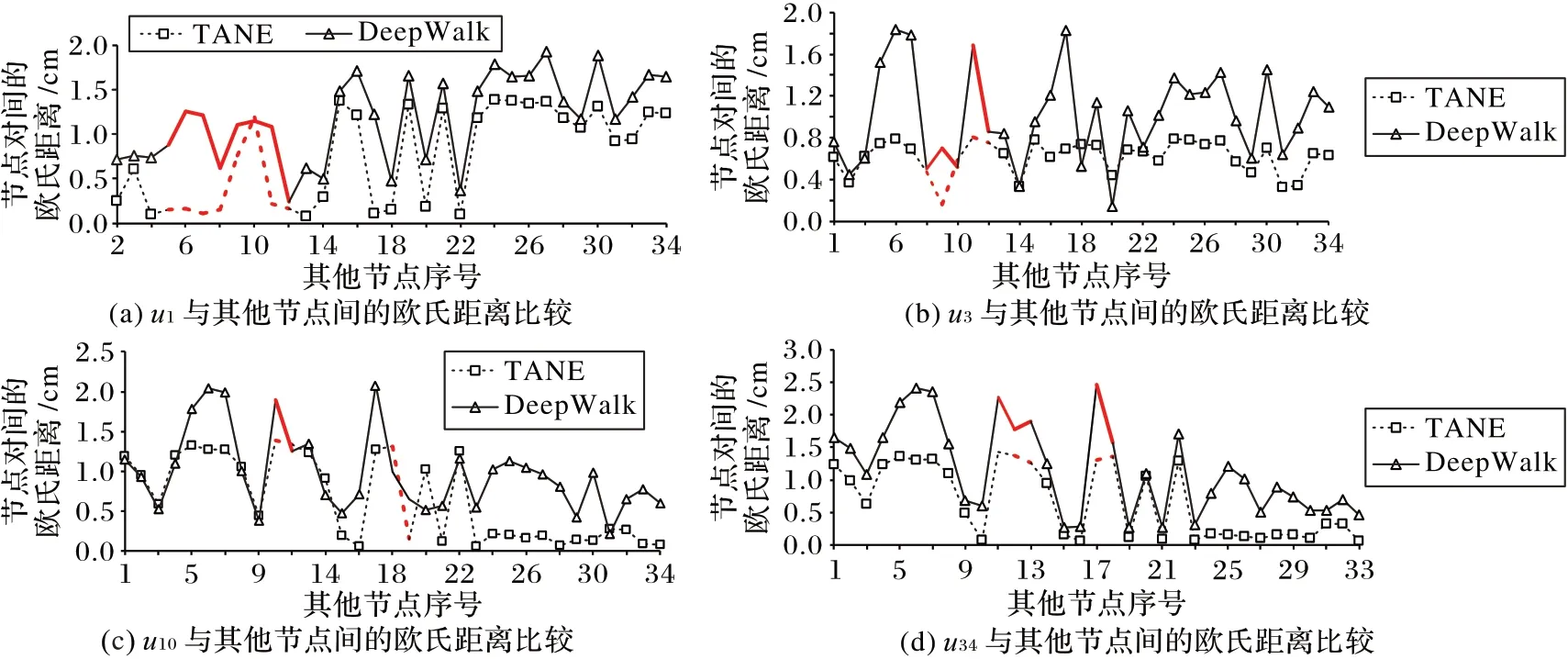
图5 在两种算法下4个节点与其他节点间欧氏距离的比较Fig.5 Comparison of Euclidean distance between four nodes and other nodes in two algorithms
4.2.2 基于聚类算法的分析
经过上述分析,在豆瓣网络上采用K-means++算法完成聚类分析任务。经过比较,选取肘部法则确定聚类簇数K,其核心指标是误差平方和(Sum of the Squared Errors,SSE),如式(10)所示;核心思想是随着聚类簇数K 的增大,SSE 值会逐渐减小并趋于平缓,拐点对应的K 值就是数据的真实聚类簇数。

首先,运用肘部法则确定Karate 网络的K 值,如图6(a)所示,拐点为4,与DeepWalk 论文中运用Modularity 算法聚成4类时Q值达到最大一致。因此,该方法具有一定的合理性。
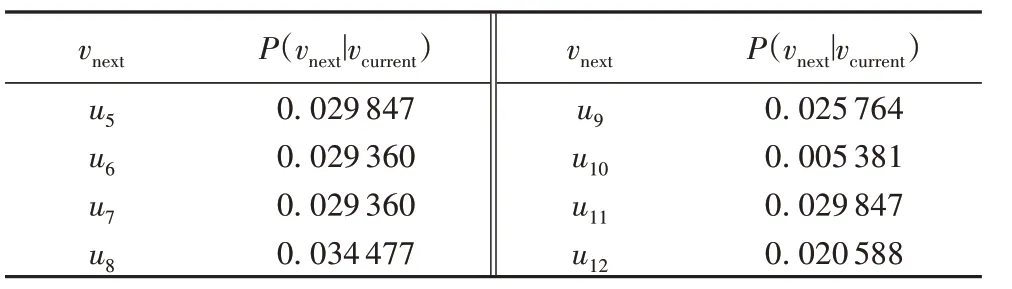
表4 u1与图5(a)中加粗线段范围内节点间的转移概率Tab.4 Transition probability between u1 and nodes in the range of bold line segment in Fig.5(a)
然后,运用肘部法则确定豆瓣网络的K 值,如图6(b)所示,为了实验的准确性,K 在拐点范围内取值,即K∈[5,13]。初始聚类中心的选择具有随机性,结果有小幅度变化,针对每个K值做了15次实验,取平均值作为最终结果。如表5所示,在K的取值范围内,TANE算法都取得了较好的结果。
综上,TANE 算法划分社区结构考虑了网络的结构和语义等方面的信息,具有实际应用价值,如在推荐系统中进行合理化、个性化推荐。
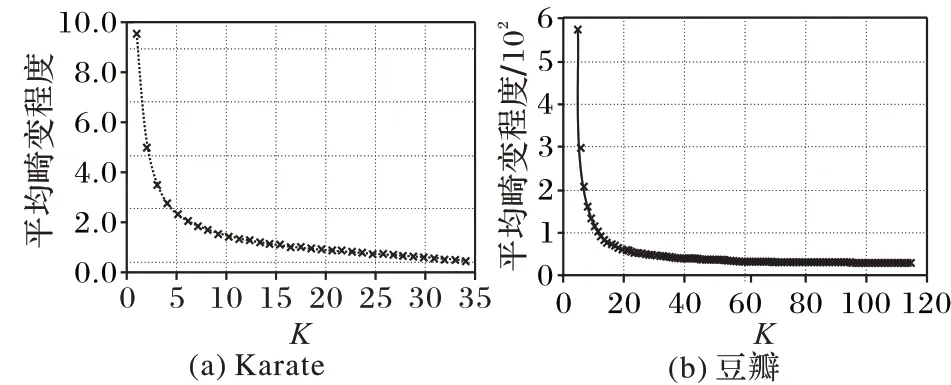
图6 用肘部法则分别确定Karate和豆瓣网络的聚类簇数Fig.6 Numbers of clusters of Karate and Douban networks determined by elbow rule
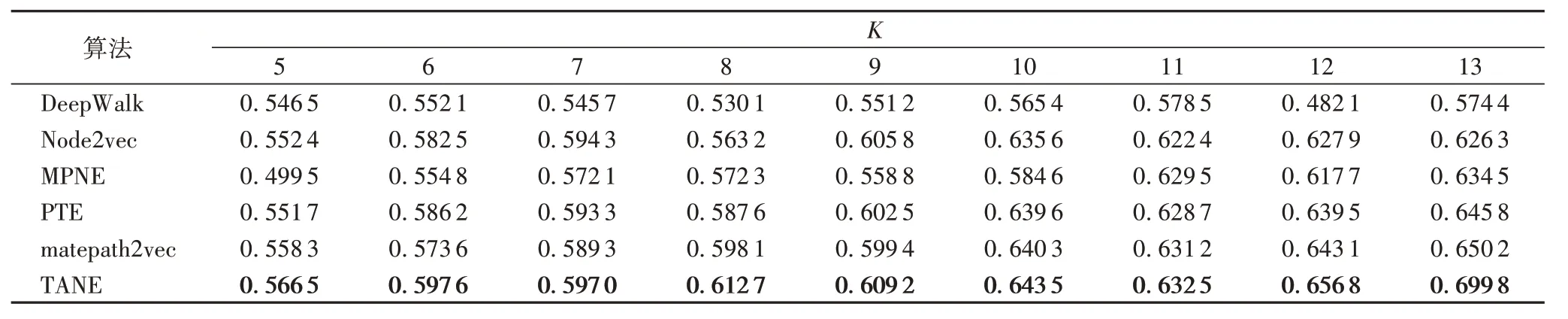
表5 豆瓣数据集上各算法获得的Q值对比Tab.5 Comparison of Q values on Douban dataset by different algorithms
4.3 参数敏感性分析
TANE 算法中涉及到多个参数。首先,对转移概率中的参数设置分5 种情况进行分析,如表6 所示:第4、5 组参数设置得到的Q值相对较小,因为网络中主题节点稀疏,在很大程度上考虑主题节点建立的联系严重影响提取网络中的信息;第1、2、3组参数设置得到的Q值相对较大,由Q2>Q1,Q1>Q3可以看出,在权衡各部分权重的前提下,基于两类节点间的关系进行建模有利于网络表示学习。最终两个数据集转移概率模型中的参数设置如表7 所示,两个数据集数据量不同,参数设置略有差异。
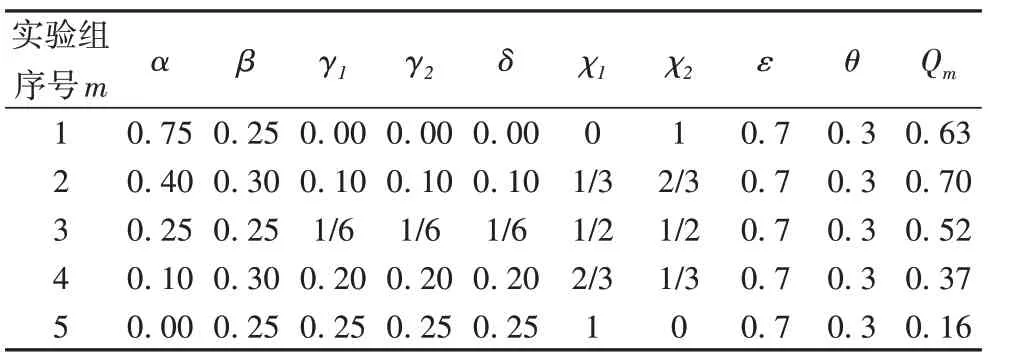
表6 转移概率模型参数分析Tab.6 Parameters analysis of transition probability model
其次,选用豆瓣数据集对Word2vec 模型中涉及几个参数进行分析。如图7 所示,Word2vec 模型中的有些参数对实验结果的影响不大,当向量维度d 取64、上下文窗口ω 取5 时,TANE 算法的表现较好。网络中节点作为起始节点的次数n、路径长度L 对实验结果影响较明显,尤其是参数L,当L>40时,Q值处于下降趋势,算法性能下降。
综上,TANE 算法中转移概率模型参数选取时根据网络中两类节点的稀疏情况来权衡建模时各部分的占比;Word2vec 模型中参数选取时结合复杂度和算法性能两方面来考虑。
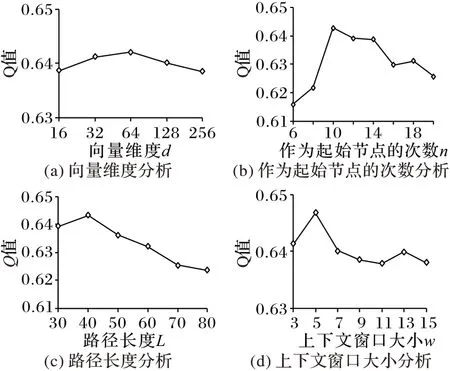
图7 Word2vec模型参数敏感性分析Fig.7 Parameters sensitivity analysis of Word2vec model

表7 转移概率模型参数设置Tab.7 Parameters setting of transition probability model
5 结语
采用集对分析理论中确定与不确定思想,给出转移概率模型,并将其运用到随机游走算法,得到了相对高质量的随机游走序列;再对游走序列进行训练,得到了主题关注网络的嵌入向量空间表示。实验结果表明,在豆瓣数据集上与5 个经典算法相比,当划分社区个数为5~13 时,TANE 算法得到的Q值均有不同幅度的提高,但数据集的稀疏性使得Q 值变化并不十分明显;当豆瓣数据集上K=13 时,TANE 算法较metapath2vec 算法的Q 值提高了近5%。综上,从结构和语义方面分析网络,可以更全面地捕捉网络中的信息,综合合理性以及实验结果来考虑,本文提出的TANE 算法取得了较好的表现。
接下来,在TANE 算法思想的基础上增大数据规模考虑异质网络的动态性和复杂性进行表示学习的相关研究是我们进一步的工作重点。

