基于Zernike矩数字图像水印的实现

王湘慧

摘要：本文以数字水印为研究对象，结合Zernike矩在图像抗旋转变化规律与特性，分析Zernike矩特性参数对获取旋转图像角度的影响，运用DCT变换实现了数字水印嵌入和提取算法，在旋转攻击后水印保持较高的相似度，验证了Zemike矩对抗旋转变化具有较好的鲁棒性。

关键词：数字水印;Zemike不变矩;DCT

中图分类号：TP309 文献标识码：A

文章编号：1009-3044（2020）03-0223-04

数字水印技术发展迅速[1]，已得到众多高等院校及研究机构的高度重视[2-5]。在数字水印整体功能越来越强大的同时，其应用的领域也越来越广泛，这就使得不同行业开始根据各自不同的需求来研究并应用数字水印技术，因此就产生了各种各样的数字水印系统[6-7]。

在抗旋转变化上Zernike矩具有明显的优势，Hu[8]于1962年提出连续函数不变矩的定义，并讨论了不变矩的基本性质，其不变矩理论被广泛应用到图像处理研究中;陈盈[9]等人提出了一种利用Zemike矩对图像几何校正的NSCT-SVD几何鲁棒盲水印算法;王胜[10]等人提出了基于边缘检测与Zernike不变矩的半脆弱图像水印认证算法;钟敏洁[11]提出了基于四元数Zernike矩的RST不变彩色图像水印方案;高光勇[12]等人利用特征域和Zernike矩，提出了一种多倍零水印版权认证方案;明细细[13]等人提出了一种结合DCT域掩膜和Zemike矩的自适应鲁棒水印算法。

DCT变换域算法能很好地抵抗有损压缩编码，吴娱[14】等人的研究和实现了基于DCT算法的视频数字水印;张春玉[15】研究了一种基于DCT变换的数字水印方法;韦晓林[16]在基本DCT算法上进行了改进，提出了n次DCT嵌入算法;侯然[17]等人提出了一种基于DWT和DCT的全盲鲁棒图像水印算法;曾祟[18]等人提出了一种基于DCT变换的图像版权数字水印算法。

本文主要研究内容是通过对图像旋转前后的Zemike矩值进行比较，来获得Zernike矩不变性关键特性参数;采用DCT算法对数字图像水印进行嵌入和提取，结合Zernike矩不变性来完成受旋转攻击的嵌入水印图像的还原角度计算，然后再提取出水印，对比提取水印与原始水印的相似度来判别这种水印嵌入算法的鲁棒性。

1 水印嵌入和解出流程

数字水印嵌入过程，将图像分为8x8图像块，并对每个小块进行DCT变换，使用Amold算法对水印图像进行置乱，将置乱后的水印图像嵌入原始图像中，每个小块中嵌入一个水印图像的像素，嵌入位置选取为具有较好鲁棒性和不可见性的（4，4）位置。图像在传输过程中，容易受到各种几何攻击，最常见的就是旋转攻击，因此对已经嵌入了水印的图像分别进行各系列的几何攻击例如旋转，平移，缩放等，恢复其大小和位置进行复原。在水印解出阶段，将含水印图像中的水印提取出，使用Ar-nold算法将其逆置乱，还原出受攻击后的水印图像，计算其与原始水印图像的相似度与误差。如图1是水印嵌入和解出流程框图。

2 Zernike矩及旋转不变性

Zernike矩是一种基于Zernike多项式的正交化函数，由于它具有抗噪性能好，冗余度小，以及旋转不变性等优点，在图像处理技术中得到了广泛的应用。

式中：m≠0，通过计算旋转角度，对已经发生旋转的图像进行逆旋转变换，即可实现将被旋转的图像进行还原摆正。

3 抗旋转实验分析及系数确定

实验中使用了MAT-LAB软件中的imrotate函数，对n和m的取值进行测算，分析n和m取值对Zernike矩的影响。通过对图像进行一定角度的旋转，利用式（9）计算偏转角度，与实际偏转角度相对比，求出其相对误差。

以lena为载入图像，取n=l和m=l的组合实验，对比其旋转1度-90度中以1度为条件变化实际旋转角度和估计旋转角度，如图2所示：

从图2可以看出，实际偏转角度与计算偏转角度呈现为一条直线，误差较小。不是所有的n和m取值组合都能获得正确计算偏转角度，当取值为（8，2）时，在1度-65度时实际旋转角度与计算旋转角度误差较小，在66。时计算旋转角度突变成了一1140.如图3所示。

为了最终确定合适的n和m值，实验中采用了lena、baboon和camman三张图像分别进行估计角度和相对误差的计算，并取其平均值的方法，根据不同的n和m所计算出的平均角度和平均相对误差如表1所示。

从表1可以看出，当n=l，m=l和n=3，m=l的时候，相对误差最小，平均角度也最接近45.5度，而其他取值的相对误差较大。本设计选取了（1，1）和（3，1）两组数据作为估计角度n和m的取值。

4 DCT变换

DCT变换是一种基于变换域的数字水印系统的相关技术，在其运算过程中只涉及实数之间的正交运算，而不像DFT变换那样还需要进行复数部分的运算，因此在运算上就更加简单、快捷。另外，DCT变换能够很好地处理图像压缩的问题，本文就是基于DCT变换，对水印进行嵌入和提取。采用DCT变换，是因为二维图像经过DCT变换后，图像的相关性低，图像的主要信息集中在直流系数和有限的几个低频系数中，并且DCT变换具有较强的抗干扰能力。

5 实验结果及分析

结合Zernike矩和DCT变换来实现数字水印的嵌入和解出，并采用旋转攻击影响图像，可以看到嵌有水印的载体图像在经过旋转之后，能够根据Zernike矩的旋转不变性，还原成旋转前的角度，虽然在图像旋转以及复原的过程中，发生了部分图像信息丢失的问题，导致了嵌入该位置的水印信息也发生了丢失，但是没有丢失的图像信息还是能够通过Zernike矩将图像较好地还原，并从还原后的图像中提取出水印。数字水印嵌入和解出的過程如图4所示，水印嵌入后峰值信噪比（PSNR）为39.2087。

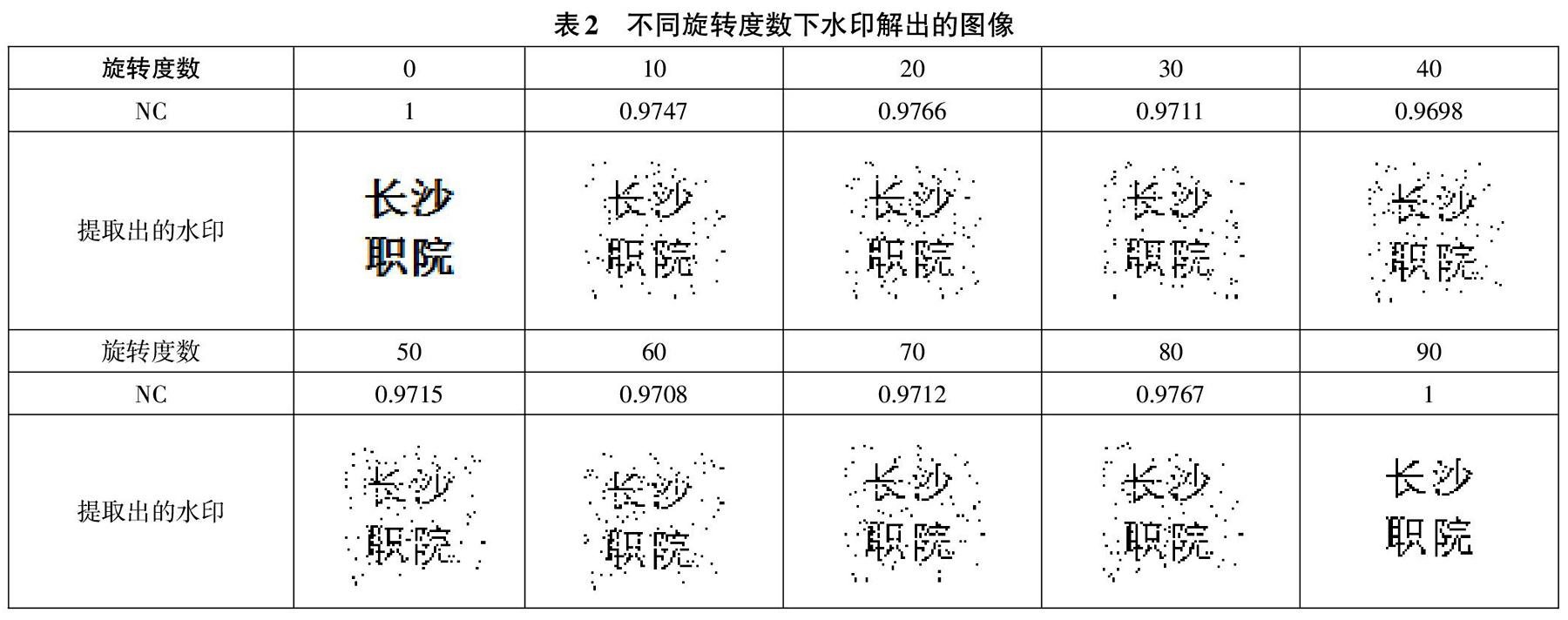
将水印解出并与原始水印进行对比获得相似度（NC）的比值，分别对图像以10。为间隔条件旋转图像，获得不同旋转角度下的水印解出图像，如表2所示。

如表2所示，旋转角度从0度增加到40度时，图像相似度从1下降到0.9698;旋转角度从40度增加到90度 时，图像相似度从0.9698上升到1。

6 结论

本文以Zernike矩为基础，研究了一种抗旋转变化的数字水印算法，其主要特点有：

1）分析了Zernike矩n和m取值对旋转角度获得的影响，发现（1，1）和（3，1）两组数据能够适用不同特性的图像;

2）在不同旋转角度的旋转攻击下，水印相似度最小值出现在40度-60度之间，其原因是旋转导致的图像信息的丢失所致。 通过对Zernike矩旋转不变性的研究，计算偏转角度后对图像进行还原和水印的提取，发现水印完整性较好，说明了该水印算法对旋转攻击具有良好的鲁棒性。

参考文献：

[1]陈明奇，钮心忻，杨义先，数字水印的研究进展和应用[J].通信学报，2001，22（5）：71-79.

[2]张春田，苏育挺，管晓康.多媒体数字水印技术[J].通信学报，2000，21（9）：46-52.

[3]黄继武，谭铁牛.图像隐形水印综述[J].自动化学报，2000，26（5）：645-655.

[4]刘瑞祯，谭铁牛.数字图像水印研究综述[J]通信学报，2000，21（8）：39-48.

[5]杨义先，钮心忻.多媒体信息伪装综论[J].通信学报，2002，23（5）：32-38.

[6]王炳锡，陈琦，邓峰森.数字水印技术[M].西安：西安电子科技大学出版社，2003：11-12.

[7]杨义先.数字水印基础教程[M].北京：人民邮电出版社，2007.

[8] Hu M K.Visual pattern recognition by moment invariants[J].IEEE Transactions on Information Theory， 1962，8（2）：179-187.

[9]陈盈，郑洪源，丁秋林，基于Zernike矩和NSCT-SVD的数字水印算法研究[J].计算机科学，2016，43（8）：84-88.

[10]王胜，解辉，张福泉，利用边缘检测与Zernike矩的半脆弱图像水印算法[J]计算机科学与探索，2018，12（4）：629-641.

[11]钟敏洁，基于四元数Zernike矩的RST不变彩色图像水印[J].计算机与现代化，2015（7）：40-43.

[12]高光勇，蒋国平，基于特征域和Zernike矩的多倍零水印版权认证方案[J]南京邮电大学学报：自然科学版，2012，32（6）：63-68.

[13]明细细，李丽娟.结合DCT域掩膜和Zemike矩的自适应鲁 棒水印算法[J]计算机工程与應用，201 1，47（19）：159-162.

[14]吴娱，平子良，李殷.基于DCT算法的视频数字水印的研究与实现[J].大学教育，2016，5（12）：133-134，140.

[15]张春玉.基于DCT变换的数字水印算法研究[J].河北农机，2019（1）：71-72.

[16]韦晓林.基于DCT的数字水印改进算法[J].电子产品世界，2019，26（2）：88-90.

[17]侯然，张洋，黄橙，基于DWT和DCT的全盲鲁棒图像水印算法[J].通信与信息技术，2019（3）：44-46.

[18]曾崇，杨伟萍.基于DCT变换的图像版权数字水印算法[J].科技通报，2018，34（6）：119-122.