Haar小波在数字图像水印算法上的探究
刘 涛
(陕西国际商贸学院,陕西西安,712046)
1 问题研究
小波变换是傅里叶变换中的特殊形式,它的优点在于可以对一些数字信号比如上文提到的数字图像或者音频之类(在数学上可以看做是函数)利用自身的变换特点:平移、伸缩,发生尺度细化作用,就相当于是一个扫描仪逐步对信号进行扫描,精确到信号上的微小细节,并且可以达到对信号低频时候进行频率细分,高频时候进行时间细分的效果。对小波变换的研究已经在全世界范围内应用到了非常广的领域内,例如信号接受处理、模式认知、图像识别、数字信息安全保护、还可以涉及到数学上的微积分方程数值解等等。
本文研究方向是通过小波变换当中应用最广的Haar小波变换把宿主图像分解,然后将保证信息安全的的数字水印信息通过算法嵌入到已分解好的宿主图像中。
2 基于Haar小波数字图像水印算法
Step1:利用Logistic变换和Arnold变换先后对数字水印信息“JD"进行之乱处理,先用Logistic变换对数字水印信息进行一级置乱,接着用Arnold变换对数字水印信息进行二级置乱,生成(0, 1)二值序列,这样做的目的是为提高信息的安全性,增加信息被破解难度。
Step2:把宿主图像分割成8*8的小图像块,目的是为了节省程序运算时间以及运算成本。接着利用Haar小波分别对8*8当中的每一个小图像块做一级解构,同时分别把CD1这样的高频图像提取出来。
Step3:利用Haar小波把Step2中提取出的高频图像再一次的解构,从而对角高频图像CD:同时选择CD1 (1,1)和CD2 (1,2),这两个位置是可以固定具体位置的系数。图1为数字图像高频分解图。
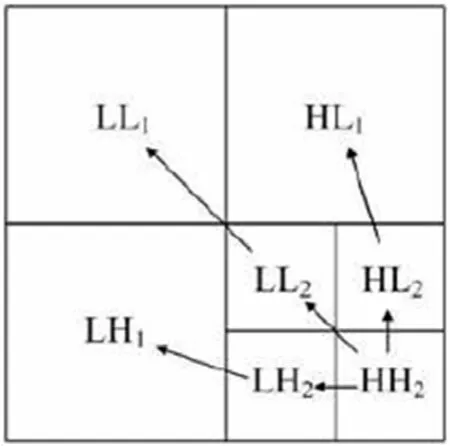
Step4:本文研究的创新之处是将数字水印信息通过算法嵌入到数字图像的高频子图区域,并且不越位的将数字水印信息读入,若计算机识别数字水印信息的读入位置是0同时CD1(1,1)<CD2 (1,2)的时侯,则交换CD1 (1,1)和CD2 (1,2)位置;当读入位为1时候,并且CD1 (1,1)>CD2 (1,2)时,则交换CD1(1,1)和CD2 (1,2)的位置。操作步骤具体为:
当Vector=0,并且CD1 (1,1)<CD2 (1,2),则交换CD1 (1,1)和CD2 (1,2)位置;
如果 Vector=1,并且‘CD1 (1,1)>CD2 (1,2),则交换 CD1(1,1)和CD2 (1,2)位置。
然后根据CD1(1,1)和CD2(1,2)之间的差值的大小决定水印的嵌入;
如果CD1(1,1)-CD2(1,2)<k,则CD2(1,1)=CD2(1,1)+(k/2);CD2(1,2)= CD2(1,2)-(k/2);
如果CD2 (1,2)-CD2 (1,1)<k,则CD2 (1,2)= CD2 (1,1)-(k/2); CD2 (1,2)= CD2 (1,2)+ (k/2)。
Step5:按照上述的嵌入算法把水印嵌入后,还要对块宿主图像作用Haar小波的逆变换,从而达到重构,这就是8*8当中的一小块宿主图像的数字水印完整的嵌入过程。
Step6:通过程序让计算机自动重复上述的流程,逐一完成8*8每一小块图像的数字水印嵌入,最终将数字水印信息嵌入整幅图像当中。
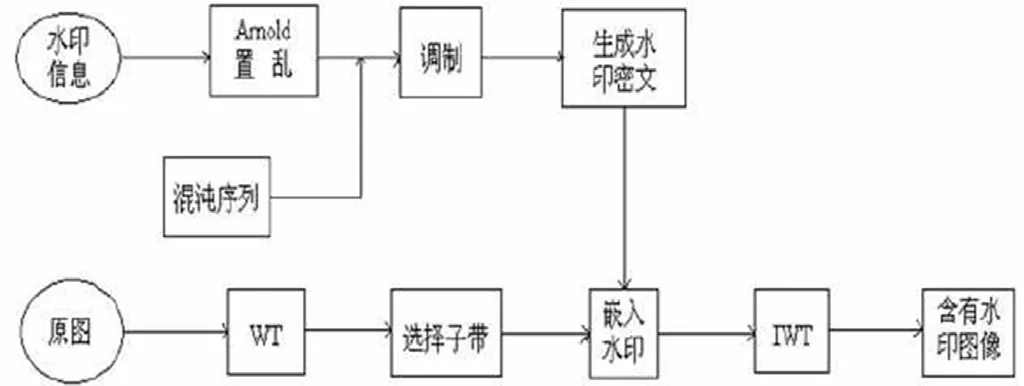
图2 为数字水印信息嵌入到宿主图像的整个流程。
本文将常用的实验的大小为512*512灰度数字图像“boon"作为宿主图像,水印信息为将大小为64*64的二值数字图像“JD”作为待嵌入的数字水印信息,图3展示。本文先对待嵌入的数字水印信息进行Logistic变换一级置乱,使之成为一级加密水印,相当于进行了第一级加密,然后对一级置乱后的数字水印信息再利用Arnold变换对其进行二级置乱,生成(0,1)二值序列,相当于是二级加密,使其具有更高的安全性。通过算法利用用Haar小波将已分割成8*8的宿主图像每一小块图像进行了两次的小波解构,在每一小块的灰度图像的高频子带区域实现了数字水印信息的嵌入。这样做的目的是利用了人类视觉独有的特点使得在数字水印信息在宿主灰度图像里具有更加理想的隐蔽性,从而达到与原灰度图像极度相似的目标。

3 数字水印信息的提取
Step1:把已嵌有数字水印信息的灰度图像,再进行8*8的减构处理,这样做的目的同样是为了降低计算机的能耗,减少资源浪费,达到最优。也为Step2做了铺垫。
Step2:对已减构好的每一小块带有数字水印信息的宿主图像,提取出其高频子带,按照系数比较法,提取之乱后的数字水印信息。最终得到完整的一维向量。
Step3:对已提取出的一维向量,按照数字水印的信息置乱的逆过程,既先进行Arnold变换恢复,再进行Logistic变换恢复,从而得到最初的待嵌入的数字水印信息“JD”。
图4为数字水印信息提取的流程图。

图4 水印信息提取流程图
4 结论
本文之所以选择灰度宿主图像的高频子带作为数字水印信息的的嵌入区域,这是结合了人类视觉特征,并且不断优化嵌入算法的结果,与以往把宿主图像的低频子带作为水印信息嵌入区域有了很大的不同。同时也验证了结合Haar小波变换,定义小波系数和数字水印信息强度因子之间的关系,加密灰度宿主图像的可行性,使得水印保密性大大加强。
[1]邸继征.小波分析原理[M],科学出版社,2010.
[2]T.LeightonJ,Cox,J.Kilian.Securedia[C].IEEE Transaction on Imagespread spectrum Processing,1997.
[3]张小华,钟桦,焦李成.数字水印与图像认证算法及应用[M],西安电子科技大学出版社,2006.
[4]瓦尔纳(David F.Walnut).小波分析导论[M].世界图书出版社,2011.

