光纤陀螺捷联惯导系统艇上系泊状态自标定方法

刘 凯,万少巍,王激扬,于 峰

(1.北京航天控制仪器研究所,北京 100039；2.海军装备部,北京 100163；3.91550部队,辽宁 大连 116023)

1 引 言

目前国内对惯导系统标定方法的研究主要集中在分立式标定,并在工程中得到应用。但在实际应用中分立式标定方法对转台精度要求较高,转位过程复杂,且当惯导系统安装在艇上或弹上后无法实现在线自标定,必须依靠定时拆卸返回厂家完成标定任务,造成了使用的极大不方便。而采用系统级标定方法通过设计合理的转位路径,利用导航误差计算器件误差,可避免对高精度转台的依赖。

近年来带转位机构的捷联惯导系统受到了广泛重视,系统级自标定方法的研究成为研究热点。国内的研究人员也提出了多种系统级标定方法:吴赛成[1]提出了一种基于Kalman滤波的27维误差参数标定模型,并设计了转位方案；江奇渊[2]提出了一种考虑加速度计二次项误差和内杆臂误差的标定方法；石文峰[3]设计了一种10位置系统级标定方法,并利用简化的误差模型和速度误差变化率方程,建立了误差参数与导航误差的关系,上述方案均要求惯导系统处于静基座条件下,在系泊条件下无法使用上述标定方案。杨玉孔[4]提出了一种针对舰船在系泊或锚泊条件下的在线标定方法,但该方法无法实现自标定,仍需依靠GPS等外部设备提供外界输入条件；袁鹏[5-6]提出了一种系泊状态下的全参数自标定方案,该方案采用低通滤波对解算的速度误差进行分解,由于海浪频率较低,采用低通滤波时不可避免会引入相位延迟,导致滤波后的速度有较大误差,无法满足标定精度,并且该标定方案无法标定惯导系统的内杆臂参数,这在动基座条件下对最终导航精度有较大影响。

本文根据实际使用条件,提出了一种15位置的动基座自标定方案。该标定方案在同时具有角运动和线运动干扰下,可标定出陀螺仪和加速度计的零偏,标度因数误差,安装误差等误差参数的基础上,增加了加速度计正负通道非对称性误差和内杆臂参数。该方法在不借助外界高精度设备的情况下,利用自身转位机构实现转位控制,完成在艇上动基座条件下的自标定任务。标定出的误差参数满足高精度惯导系统的要求。

2 惯导系统误差模型

2.1 惯性器件误差模型

带转位机构的光纤陀螺捷联惯导系统由3个光纤陀螺,3个石英加速度计,轴端角度传感器及电机组成。这里主要针对光纤陀螺和石英加速度计的零偏、标度因数误差、安装误差、加速度计非对称系数误差及内杆臂误差等误差项进行建模。

定义以载体坐标系b系(Oxb,yb,zb)为参考坐标系,令X加速度计敏感轴与载体坐标系的Oxb轴重合,Y加速度计敏感轴在Oxbyb平面内,Z加速度计与X加速度计、Y加速度计敏感轴组成右手直角坐标系,这样可将6个安装误差简化为3个安装误差角[7]。则加速度计输出的误差模型为:

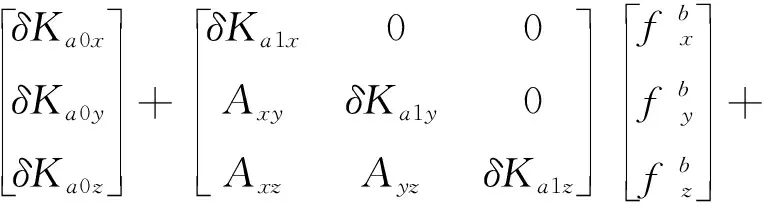
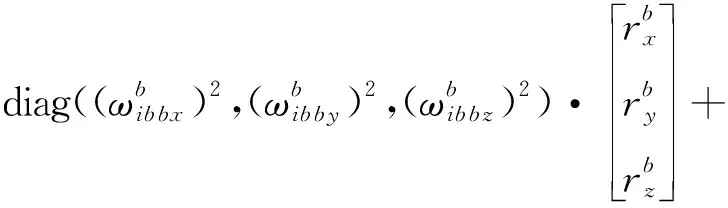
(1)

陀螺仪误差模型为:

(2)

2.2 系统误差方程

选取东北天坐标系为导航坐标系n系,本文不加推导的直接给出系统姿态误差方程为:

(3)

速度误差方程为:

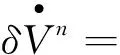
(4)

位置误差方程为:

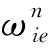
3 系泊条件下的速度误差获取

在系泊状态下对舰艇的角运动及线运动情况进行数据采集,并对采集数据进行分析可知,艇体水平方向的最大变化量为0.18 m,频率约为0.059 Hz；升沉方向的最大变化量为0.15 m,频率约为0.071 Hz。艇体的角运动通过FFT分析可知,每个方向主要由3个正弦波叠加而成,纵摇角最大幅值为1.1°,频率约为0.083 Hz；横摇角最大幅值为2.8°,频率约为0.067 Hz；偏航角最大幅值为0.48°,频率约为0.083 Hz。

通过对艇体运动数据进行分析可知,在系泊条件下的线运动幅值相对较小,频率在0.05 Hz以上,而真实速度相对于速度误差是高频分量,可以采用滤波手段对艇体线运动信息进行剔除。首先设计IIR低通滤波器,令通带截止频率为0.01 Hz,阻带截止频率为0.05 Hz,通带最大衰减为1 dB,阻带最小衰减为80 dB。设计的低通滤波器能将外界带来的线运动滤除掉,但是由于阻带截止频率过低,滤波的同时不可避免会造成相位延迟,经仿真分析带来的延迟超过100 s,这对于标定来说是不可接受的。

针对在处理解算速度使用的滤波器引起相移问题[8],提出了使用零相移低通滤波器对解算速度进行处理。零相位数字滤波的方法是先将信号正向通过滤波器,将正向滤波所得结果进行时域翻转后再次通过滤波器,得到二次滤波结果,再将二次滤波结果再次进行时域翻转,可得到零相移的信号[9]。零相位数字滤波器在频域内的描述为:

(6)

其中,X(ejω)为输入信号;H(ejω)为所用的数字滤波器冲击响应序列；Y2(ejω)为进行时域翻转后的信号;Y3(ejω)为第二次滤波后的信号;Y4(ejω)为第二次滤波结果再进行时域翻转的信号。

由上述公式可得:

Y(ejω)=X(ejω)|H(ejω)|2

(7)

由此可见,输出Y(ejω)与输入X(ejω)不存在附加相位。

为验证设计的零相位低通滤波器,对某型惯导系统在系泊状态下的速度输出进行IIR低通滤波和零相位滤波处理,可以看出使用零相位滤波的速度误差基本没有相位延迟,而采用IIR低通滤波器的速度误差相位滞后明显,必然会造成标定结果不准确,图1表示在不同滤波器下的速度误差。

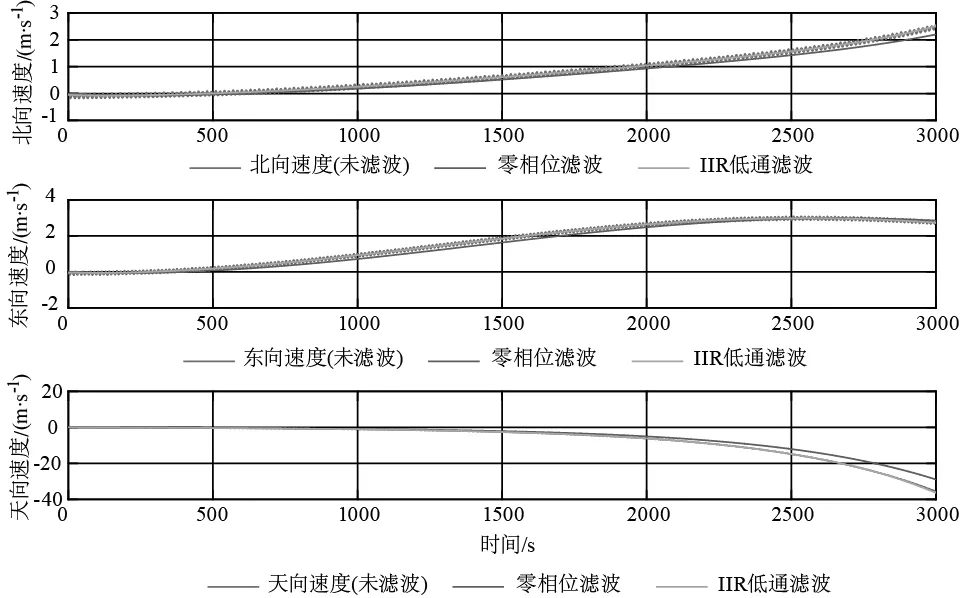
图1 不同滤波器下的速度误差

由图1可知,零相位滤波相对IIR低通滤波器来说,在相位上没有延迟,且能将真实速度从解算速度中率除掉,得到由器件误差引起的速度误差。通过比较可以发现,采用IIR低通滤波器与零相位滤波器得到的速度误差之差最大可达7.4185 m/s,这对于标定出精确的误差参数来说明显过大,故采用零相位滤波器能得到更好的结果。

4 滤波器设计

考虑惯导系统中的所有误差参数,包括陀螺和加速度计的零偏,标度因数误差,安装误差,加速度计非对称误差,内杆臂误差以及系统的失准角,速度误差和位置误差共36维,选取的状态变量如下式所示:

(8)

通过对解算的速度进行滤波后,则导航解算误差可得由惯性器件误差引起,选取滤波后的速度误差为观测量,故:

Z=[δVEδVNδVU]T

(9)

根据前面推导的误差方程,可得系统的状态方程为:

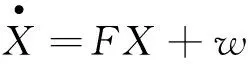
(10)

其中,矩阵F可根据公式(1)～(5)得到,w为36×1维的零均值白噪声。

系统量测方程为:

Z=HX+v

(10)

其中,H=[03×3I3×303×30];v为3×1维的零均值白噪声。

5 标定路径设计及可观测性分析

采用带双轴转位机构的捷联惯导系统,便于在系泊状态实现转位控制,可有效激励出惯性器件的所有误差项。根据转位机构的特点,现设计一15位置自标定方案。为了保证所设计的标定路径能激励出惯性器件所有误差项,需要系统完全可观测。

利用PWCS手段对系统的可观测性进行分析,该方法将线性时变系统所提取的可观测矩阵代替系统总的可观测矩阵来分析可观测性,可简化分析过程,便与实际应用。根据设计的Kalman滤波方程可知,当在每个位置Rank(Qs(r))为满秩,则系统完全可观测。根据设计的转位路径进行分析,可得在不同位置下系统的秩如表1所示。

表1 转动次序

从表1可以看出,经过15位置后,系统的秩达到满秩,这说明所建立的误差方程中的误差系数是完全可观测的。

6 仿真及实验验证

6.1 仿真验证

为模拟真实系泊状态下艇体的运动环境,根据已采集的海浪条件,经过FFT分析可得到海浪的运动条件。按照实际条件设置仿真条件,角运动条件如下:

(11)

线运动条件为:

(12)

标定的总时长为5400 s,每个位置所在的时间均等。按照标定路径设置仿真条件,以及陀螺仪和加速度计的输出,并采用多次迭代的方法而到最终标定结果,表2仿真结果对比表。

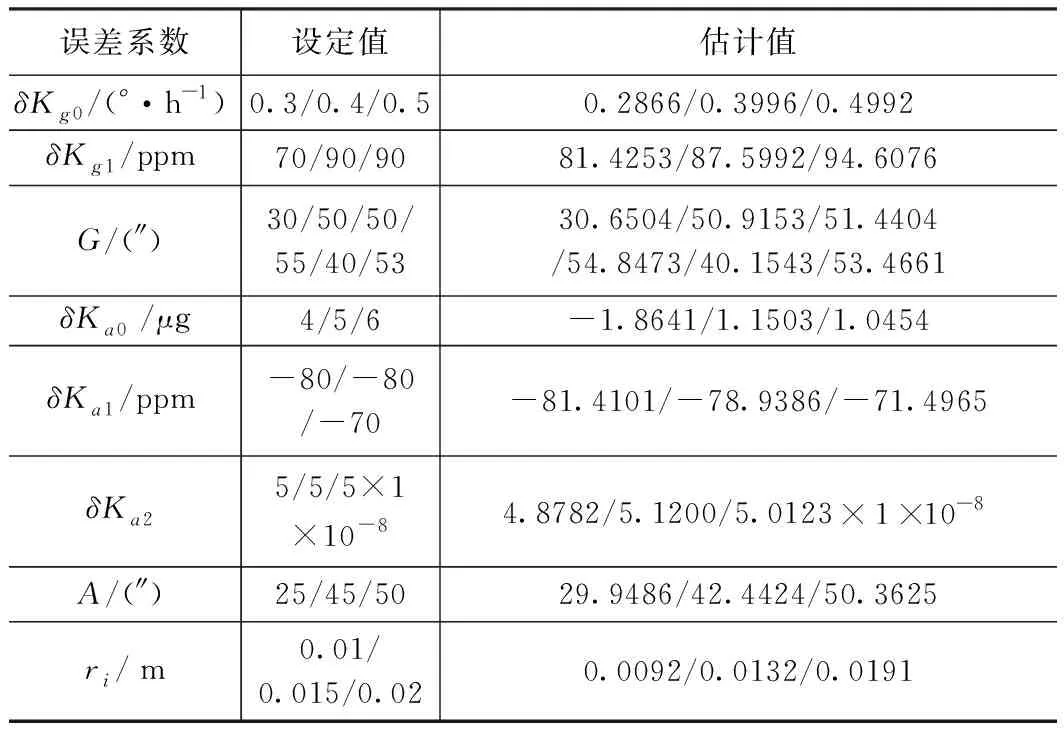
表2 仿真结果对比

从表2可以看出,陀螺仪零偏估计精度优于0.015°/h,标度因数估计精度优于5 ppm,安装误差估计精度优于1.5″,加速度计零偏估计精度优于5 μg,标度因数估计精度优于2 ppm,加速度计非对称误差估计精度优于2×10-9,安装误差估计精度优于5”,内杆臂误差优于0.002 m。各误差系数收敛结果如图2～7所示,各误差项在最后一次迭代时均已收敛到零,已将各误差项估计出来。

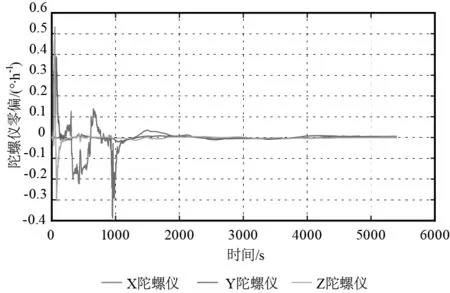
图2 陀螺仪零偏估计结果

图3 陀螺仪标度因数误差估计结果

图4 加速度计零偏估计结果

图5 加速度计标度因数误差估计结果

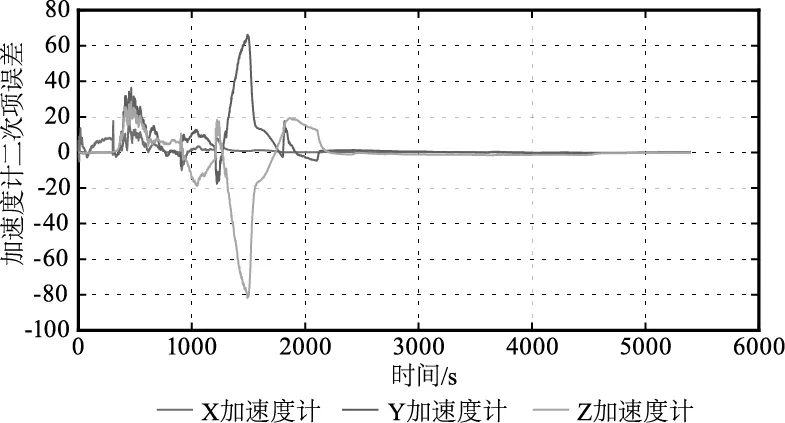
图6 加速度计非对称误差估计结果

图7 内杆臂误差估计结果

6.2 实验验证

为验证标定方法的有效性,将某型双轴光纤捷联惯导系统安装在六自由度转台上,按照文中所述的标定方法开展标定试验。由于六自由度转台只能实现单个正弦波或余弦波,无法实现多个正弦或余弦波的叠加,故角运动采用幅值最大的正弦波,线运动条件与仿真条件保持一致。初始相位为零,在静基座条件下完成初始对准后,六自由度转台启动开始动基座标定试验。将在六自由度转台下的标定结果与静基座条件下已有的标定结果做对比,如表3所示。

表3 静基座与系泊状态下标定结果对比

7 结 论

本文提出了一种在系泊条件下的光纤陀螺捷联惯导误差参数标定方法,该方法在标定出陀螺仪和加速度计的零偏,标度因数误差和安装误差的基础上,增加了对加速度计非对称误差和内杆臂效应误差项的标定。该方法并改进了在系泊条件下获取误差速度的方法,使得误差速度的获取不会有明显的滞后,增加了标定的准确度。仿真及实验结果表明,设计的转位路径合理有效,能有效激励出惯性器件的所有误差项,并能对误差模型中的所有误差系数进行有效估计。通过与静基座标定结果对比,在系泊状态下,各误差项标定结果与静基座状态一致,证明了标定方法的有效性,具有实际的应用价值。