激光脉冲弱小回波信号提取方法研究

邵艳明,王 爽,王 兴,陈宗镁,余 跃

(1.上海航天控制技术研究所,上海 201109;2.中国航天科技集团公司红外探测技术研发中心,上海 201109)

1 引 言

在激光红外复合制导中,激光三维雷达探测系统具有分辨率高、探测距离远的特点[1-2],且目标和红外诱饵对于激光的回波信号具有较大的区别[3],因此增加激光三维雷达制导的模式,有助于提升导引头的目标识别和抗干扰能力。

在脉冲式激光雷达的探测过程中,回波信号的强度与目标的尺寸和反射特性有很大的关系,此外,随着探测距离的增加,激光脉冲的回波信号也将变弱,加之激光发射系统的高频脉冲电路中可能存在的电磁干扰信号,系统检测到的回波信号的信噪比通常处于一个较低的水平。目前常规的激光测距系统中,准确的回波位置检测是确保测距精度的关键,通常采用峰值检测的方法来确定回波位置,并结合脉冲的飞行时间计算得到目标的距离信息,当处于低信噪比的情况下时,测量精度较低,激光雷达的探测距离难以提升。

目前许多学者针对微弱激光脉冲回波提出了基于相关检测的方法[4-6],这些方法能在一定程度上提升回波信号的信号噪比,但也存在一些不足之处,诸如时间漂移问题,或是需要对发射脉冲串也进行记录。也有学者提出了一种基于改进奇异值分解和自适应小波阈值去噪的激光雷达回波信号提取方法[7],可以将回波信噪比由6.336 dB提升到17.448 dB,但是并未对更低信噪比的回波信号进行试验。

本文结合现有的激光测距去噪方法,提出了一种基于自相关滤波与奇异值分解的数字信号处理方法,首先通过仿真数据验证该方法的有效性,然后应用于实际采集的激光脉冲回波信号。结果表明,本文方法可以将包含微弱脉冲的回波信号的信噪比显著提升。由于三维成像雷达与点源激光测距方式中的每一个像素的处理方法都是一样的,因此本文方法对于扫描方式的激光和单点激光测距均适用。

2 脉冲式激光测距原理

激光雷达系统通常由激光发射器、接收器和数据处理系统三部分组成,而脉冲式激光测距的原理是用激光器向被测目标发射单个或多个脉冲宽度很窄的激光脉冲,通过测量激光脉冲从发射时刻到由目标反射后返回接收机所经过的飞行时间,计算出目标的距离:

R=c·Δt/2=c·(t2-t1)/2

(1)

其中,R为所测量的目标距离;t1为激光脉冲的发射时刻;t2为激光脉冲的接收时刻;Δt=t2-t1为激光脉冲往返的飞行时间;c为激光在空中的传播速度。

距离测量的精度用相对误差,也即距离测量的误差同该距离长度的比值来表示,比值越小测距精度越高。激光雷达的测距精度ξ与距离分辨率Δ和信噪比SNR之间存在如下关系:

(2)

由此可见,为了提高激光雷达的测距精度,需要采取有效措施来提高回波信号的信噪比。此外,随着测量距离的增大,回波信号将不断变弱,提升激光回波的信噪比也有助于增加测量距离的范围。在通常情况下,激光回波信号总是受到杂波和噪声干扰,因此需要对激光脉冲的回波数据进行滤波处理,提高回波的信噪比,从而提高激光雷达的测距精度和测距范围。

3 激光脉冲弱小回波信号滤波方法

为了对激光回波中的脉冲信号进行提取,本文在现有激光微弱脉冲回波的提取方法基础上,将自相关检测方法与改进的奇异值分解方法相结合,并采用仿真数据对该方法的去噪效果进行了分析。采用信噪比(SNR)与均方根误差(RMSE)对去噪效果进行衡量,去噪效果与信噪比成正比关系,与均方根误差成反比关系。

3.1 改进的奇异值分解方法

奇异值分解(Singular Value Decomposition,SVD)方法在信号噪声的消除上有着较为广泛的应用,具有计算速度快、效果稳定的特点,实质上是一种矩阵分解的方法[8],若信号矩阵A符合式(3)所示的形式,则表明矩阵A可以被分解为三个矩阵的乘积。

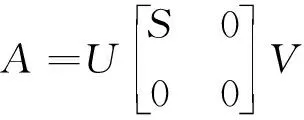
(3)

其中,U、V为酋矩阵,S=diag(σ1,σ2,…,σr)表示奇异值矩阵;r为矩阵A的秩,且σ1≥σ2≥…≥σk≫σk+1≥…≥σr,其中前k个奇异值主要反映有效信号,后面r-k个奇异值较小,主要反映噪声[9]。因此通过一定的原则对奇异值矩阵S进行筛选,仅保留数值偏大的奇异值,将数值偏小的奇异值置零,便可从信号矩阵A中重构出消噪后的有效信号。对于激光回波信号,奇异值分解主要分为Hankel矩阵构造、奇异值分解和信号恢复三个主要步骤,所构造的Hankel矩阵形式如下:

(4)

其中,N为激光回波信号的长度;n=(N+1)/2。

在低信噪比情况下,弱小回波信号淹没于噪声中,传统的奇异值滤噪方法有可能将有效回波信号也滤除,因此本文采用了一种基于曲率谱的奇异值选取方法,首先计算奇异值的曲率谱,然后使用差分方法(different method)找到曲率谱的峰值序列θp(σk),p=1,2,3,…。设定峰值序列的阈值θT,找到大于该阈值的最小峰值所对应的序号作为分界点,将大于该序号的奇异值置零,得到新的Hanker矩阵。其中阈值θT设为0.008·max(θp(σk)),曲率计算公式如下:

(5)

3.2 自相关检测技术

激光雷达回波信号的噪声来源主要是环境背景噪声和内部噪声,内部噪声主要由回波脉冲接收机中的相关电路和馈线等产生,这类噪声一般为高斯白噪声。

设单个脉冲信号sij的幅度为A,为了满足相关计算的要求,相邻两次采集的起始时间间隔需与相邻两个脉冲的发射时间间隔一致,对于实际采集的离散信号xij,第i个脉冲的第j个采样值经过N个回波信号的累加后,可以表示为:

(6)

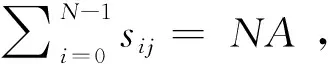
通过增加进行相关计算的脉冲个数,可以有效提高信噪比,降低信号提取的难度,但同时也需要考虑增加脉冲个数所带来的累积时间的增加。

4 仿真实验

4.1 仿真环境

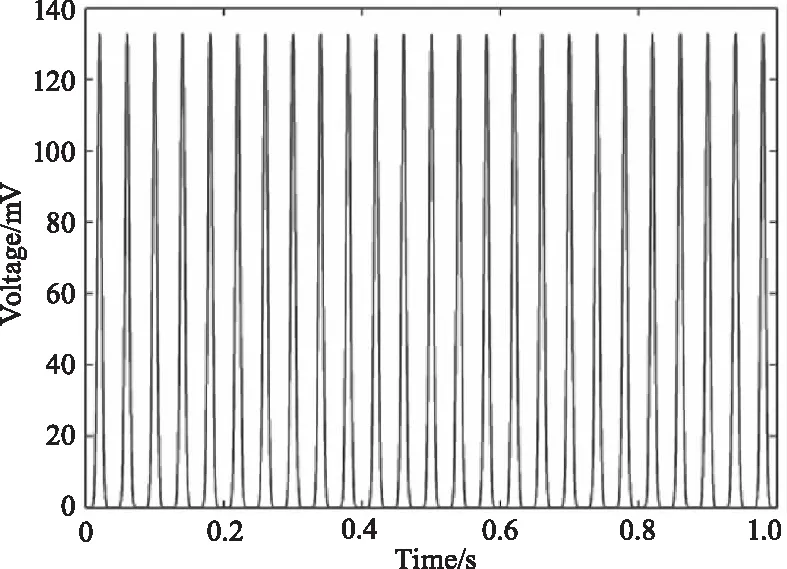
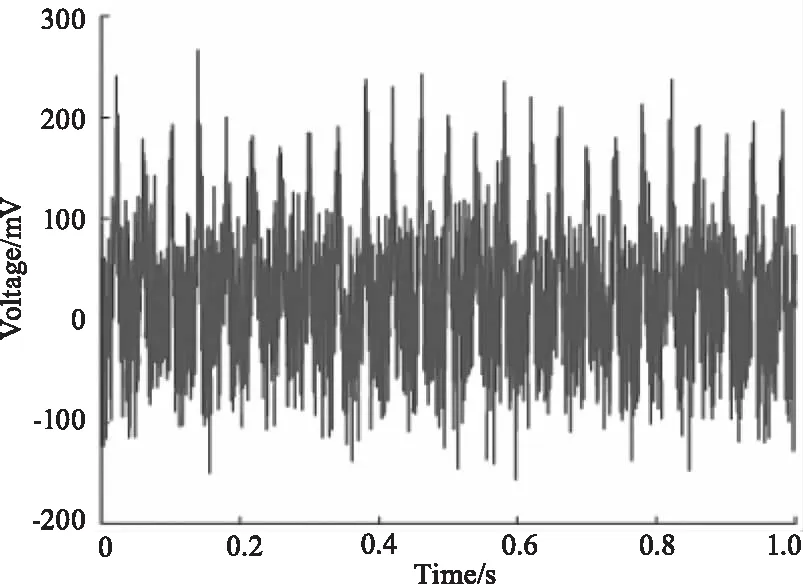
图1 原始脉冲信号

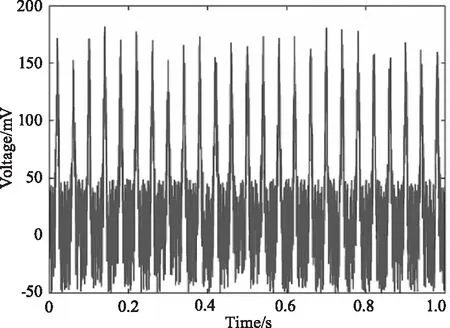
(a)噪声幅值0.05 mV

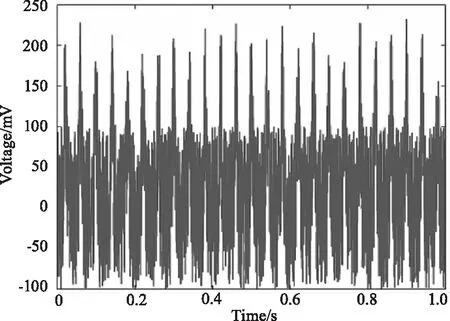
(b)噪声幅值0.1 mV

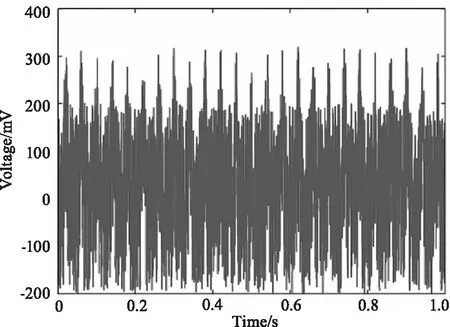
(c)噪声幅值0.2 mV

4.2 仿真结果分析

为了从弱小回波信号中提取出有效地脉冲信号,本文比较和分析了将SVD 分解方法、相关检测法应用于脉冲信号的滤波去噪效果。

4.2.1 SVD方法

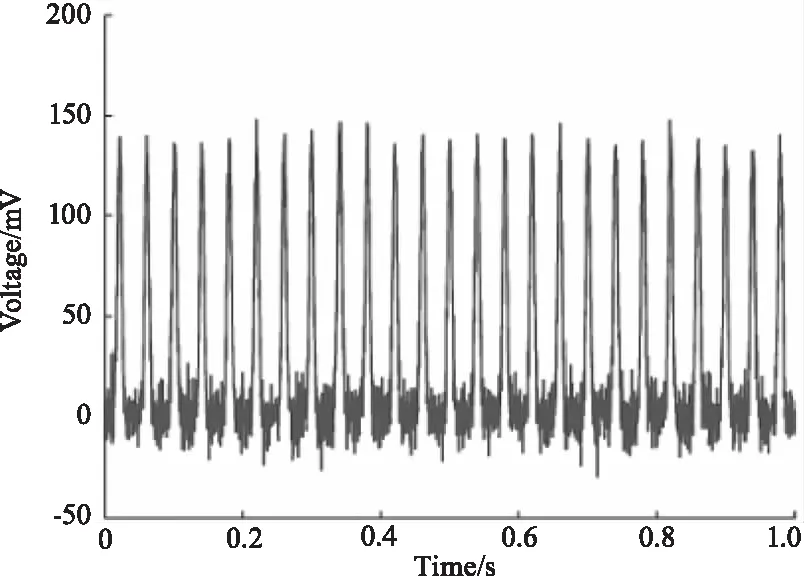
利用改进的奇异值分解方法对不同加噪情况下的仿真激光回波信号进行分析,首先将激光回波信号重构为n×n维度的Hankel矩阵,对于本文的仿真数据,n=1250；然后进行奇异值分解,得到奇异值序列。为了找到合适的奇异值分界值,依据曲率谱的峰值找到相应的奇异值,然后重构得到如图3～5所示的滤波结果,对应的信噪比和均方根误差如表1～表3所示。

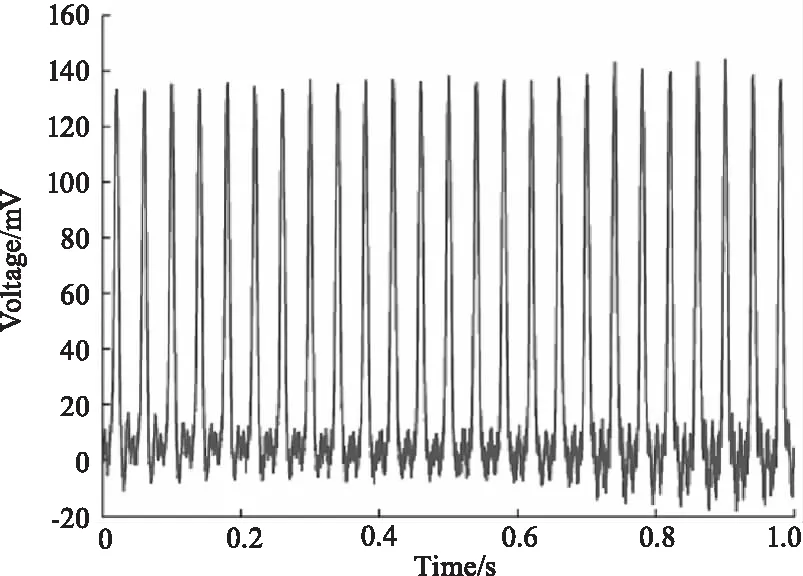
图3 噪声幅值0.05 mV时的SVD去噪结果

图4 噪声幅值0.1mV时的SVD去噪结果

4.2.2 相关检测方法

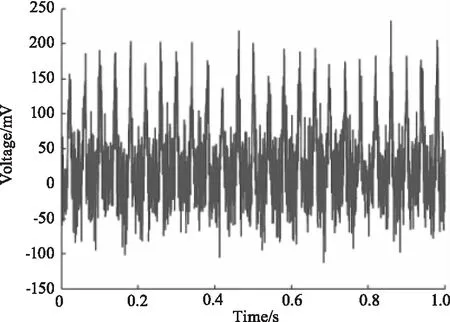
对于三种不同加噪情况下的脉冲回波信号应用相关滤波检测,得到如图6～图8的处理结果,图中从左到右依次为采用5、10、50个脉冲进行相关滤波。去噪后的信号的信噪比和均方根误差分别如表1～表3所示,由表中数据可知,随着相关的脉冲个数的增加,信号的信噪比得到提升,均方根误差下降,表明提升相关脉冲的个数有助于滤波效果的提升。

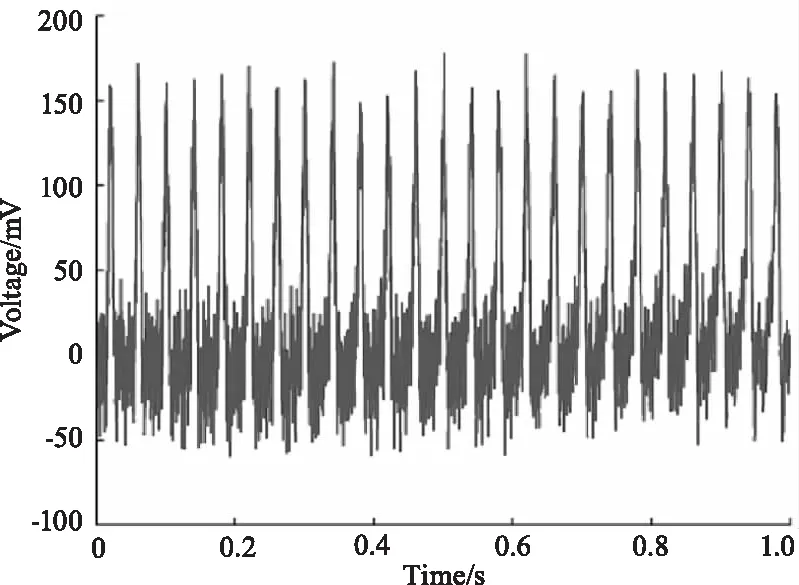
图5 噪声幅值0.2 mV时的SVD去噪结果

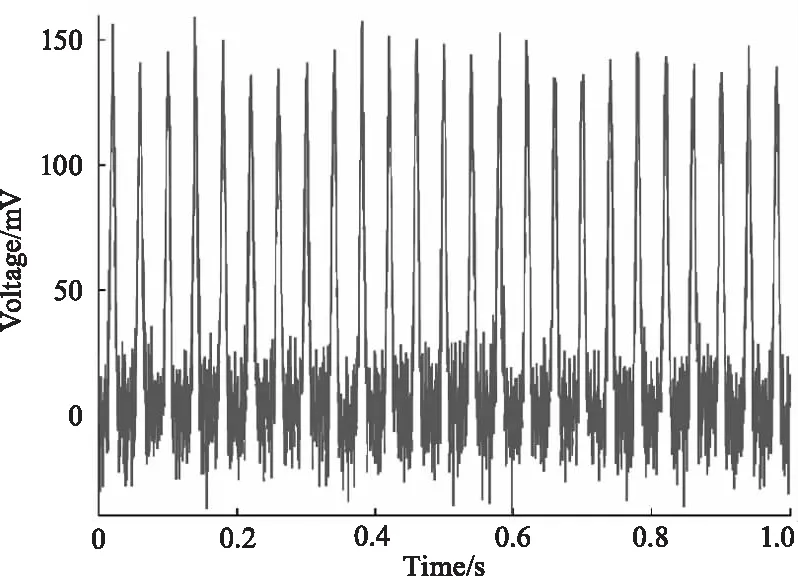
(a)5次相关滤波

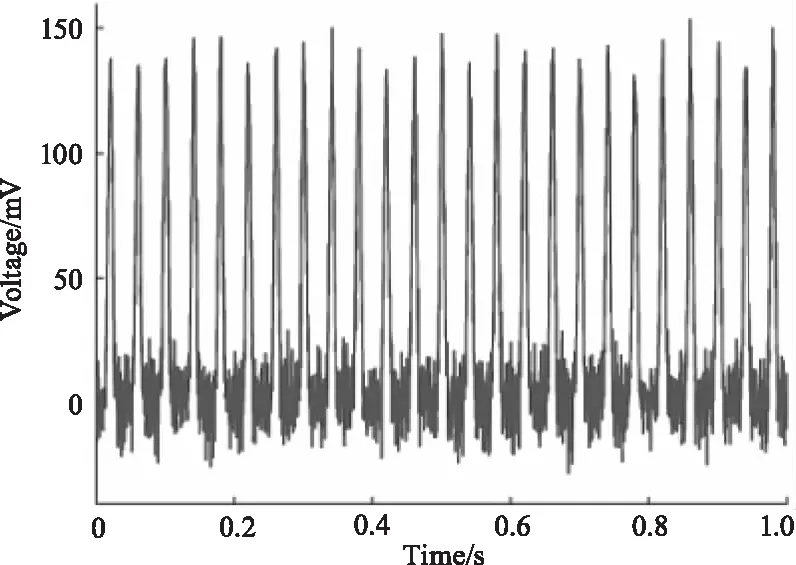
(b)10次相关滤波

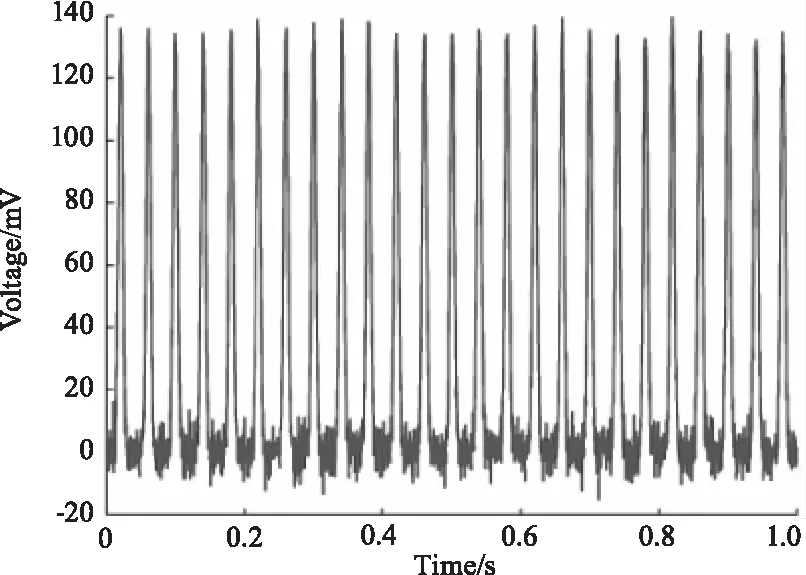
(c)50次相关滤波

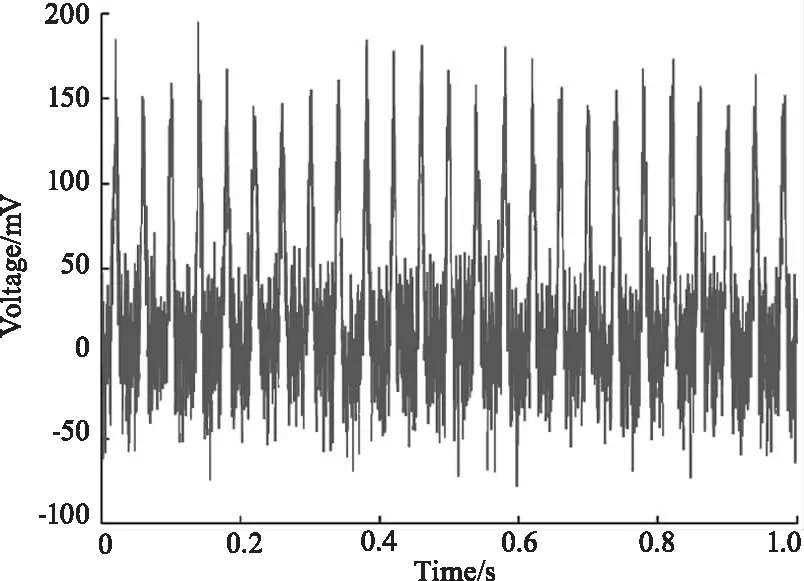
(a)5次相关滤波

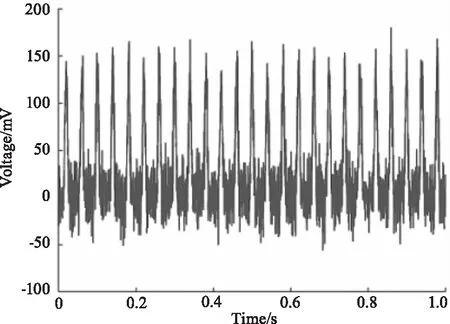
(b)10次相关滤波

(c)50次相关滤波

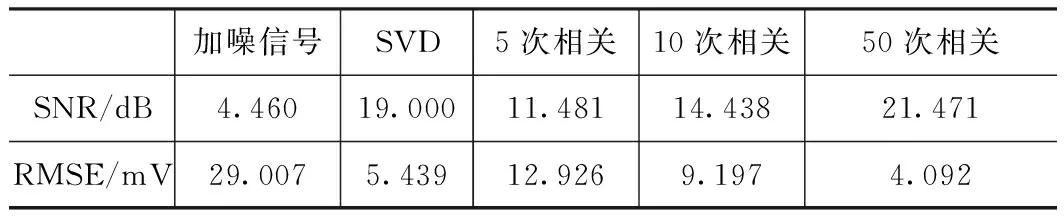
表1 0.05 mV噪声信号处理效果

表2 0.1 mV噪声信号处理效果

(a)5次相关滤波

(b)10次相关滤波

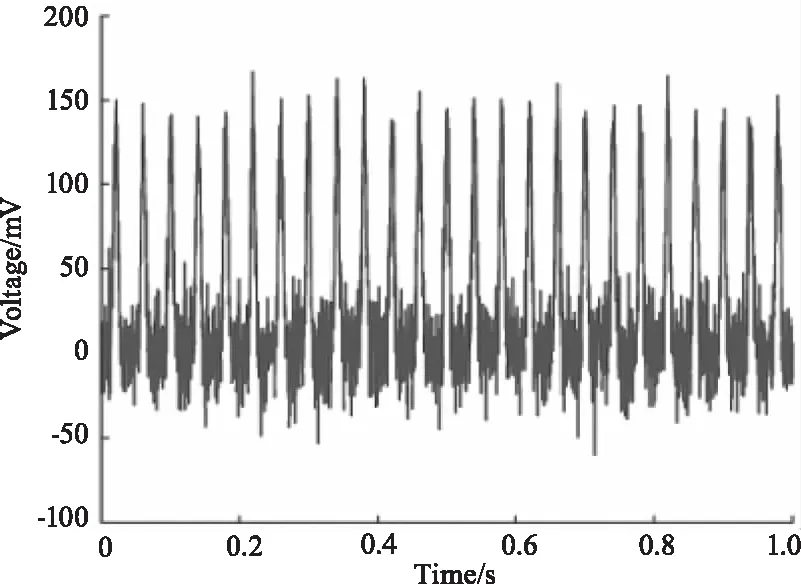
(c)50次相关滤波

对于图8中用5次相关滤波的检测结果,再采用一次奇异值分解方法,可以得到如图9所示的去噪结果,信噪比SNR=14.173 dB,均方根误差RMSE=9.481 mV,提升效果显著。

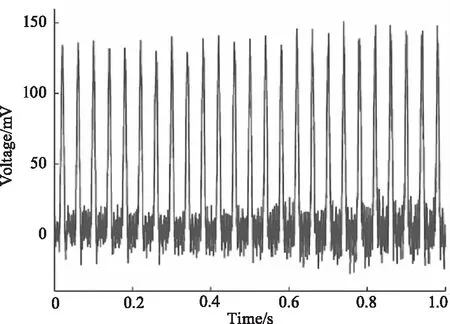
图9 结合5次相关滤波及SVD处理后的脉冲信号

表3 0.2 mV噪声信号处理效果

Tab.3 Denoising results of 0.2 mV noisy signal

加噪信号SVD5次相关10次相关50次相关SNR/dB-7.5926.754-0.5602.3969.430RMSE/mV116.17322.27651.70536.78816.369

4.3 实验数据分析

为了进一步验证上述方法的有效性,采用了实际采集的激光回波数据进行验证,发射激光脉冲频率为1×106Hz。采用的示波器型号为:Tektronix MSO 4054 Mixed Signal Oscilloscope,采样频率为10 kHz。采集得到的回波脉冲信号如图10所示。

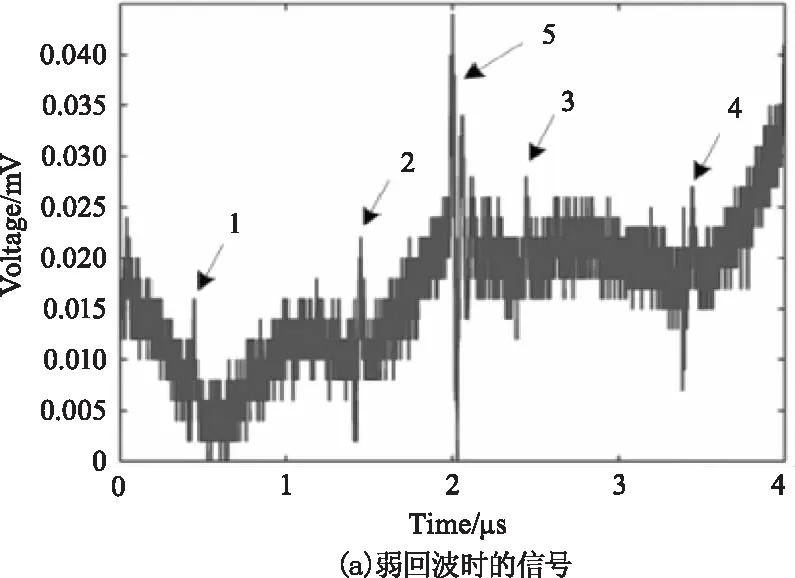
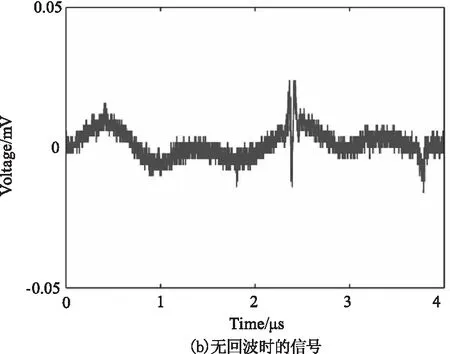
图10 示波器采集回波信号

其中图10(a)为弱回波时的输出信号,在0.5、1.5、2.5和3.5 μs处的特征峰1,2,3,4分别为四个回波脉冲的位置,在2 μs处的特征峰5为电路噪声引起的波峰,后续需通过电路处理提前消除；图10(b)为无回波时的信号；图10(c)为强回波时的输出信号。

从图10中可知,强回波信号无需滤波去噪处理即有良好的信噪比,直接采用阈值分割法就能够有效地提取回波脉冲,而弱回波信号中除了高斯白噪声外,还存在着有色噪声,因此需要先去除有色噪声,然后再结合相关检测及奇异值分解方法去噪,提取出最终的脉冲信号。

4.3.1 去除有色噪声

考虑到弱回波信号中除了有效脉冲外的信号与无回波时的信号并不一致,采用拟合的方式,拟合得到有色噪声的趋势,再用弱回波信号减去该趋势,提取出回波中的脉冲信号。如图11所示为采用阶数为10的多项式拟合结果。

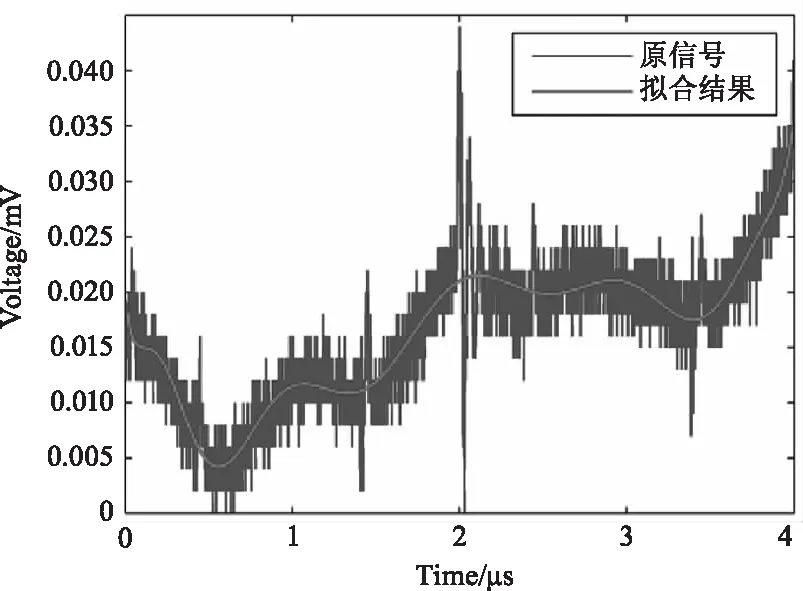
图11 拟合结果

4.3.2 去除白噪声

将弱回波信号与拟合结果相减,并以步长20进行平滑滤波,得到的滤波结果如图12所示。将四个脉冲按信号周期中的同一时刻对齐,得到如图13所示的叠加结果,可见脉冲的峰值位置相互重叠。再经过相关处理后得到如图14所示的增强结果,在第2个脉冲周期的结尾处以及第3个脉冲周期的起始处,由于存在电路噪声的干扰,相关理后,左端仍然存在若干起伏,右端也存在一处起伏较大的地方,但幅值明显比原信号中的干扰幅值衰减了很多。图15为对4次相关处理后的结果再进行奇异值去噪的最终结果,从图15中可知,脉冲信号中的噪声和右侧的干扰得到了有效地抑制和平滑,但是由于左侧干扰的幅值和分布范围较大,难以很好的消除。在后续的硬件电路升级处理中,若是能够将回波脉冲中所夹杂的电路噪声信号去除后再结合本方法,则得到的回波脉冲信号将具有更好的信噪比。

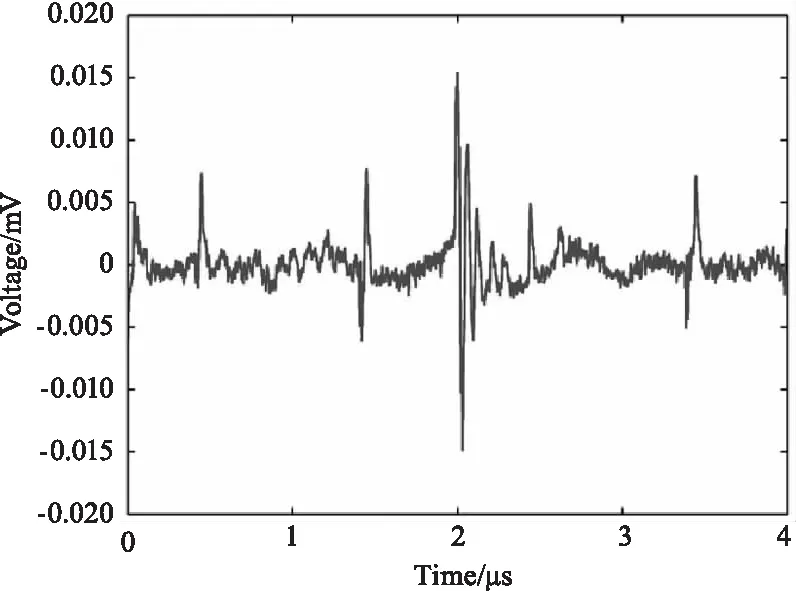
图12 对相减后的信号进行平滑后的结果

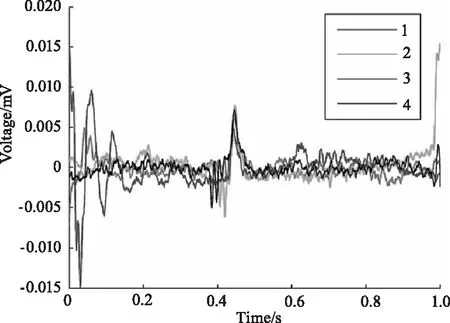
图13 单个回波脉冲叠加图

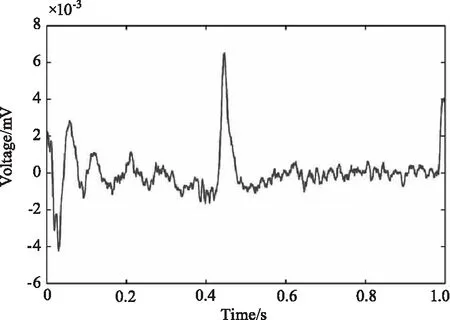
图14 对回波进行4次相关滤波的结果

5 结 论

为了提高远距离探测情况下弱小回波脉冲信号的信噪比,本文提出了一种基于相关滤波与奇异值分解的方法,结合仿真数据和实际采集的回波信号对本文方法的有效性进行了验证,其中对于实际采集的微弱回波信号,先采用拟合的方法去除背景噪声,然后再结合本文方法提升信噪比。实验结果表明,对于低信噪比情况下,本文方法能够显著提升信噪比。在后续的研究中,还可以从合理设计电路,减少电路噪声的影响,并通过提高激光脉冲的重频,增加相关滤波的脉冲个数的方法,进一步提升本文方法的效果。

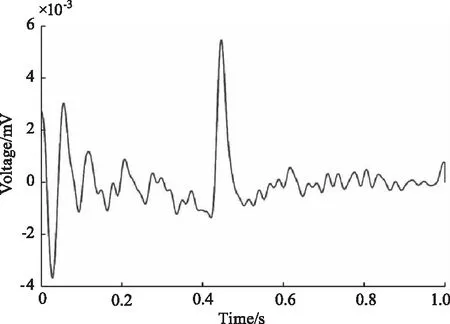
图15 相关滤波后采用SVD滤波结果