GARCH模型族及其在金融市场中的应用研究综述

聂巧平，胡冰倩

（天津商业大学经济学院，天津 300134）

在传统计量经济学模型中，均假定扰动项的方差为常数，然而许多经济时间序列的波动性有聚集现象，在这种情况下，假定方差为常数是不恰当的。针对这种情况，Engle[1]在1982年最先提出了自回归条件异方差（Autoregressive Conditional Heteroskedastic Model，ARCH）模型。并推广到对金融时间序列数据波动性的分析中，ARCH模型作为实证金融计量学的主要工具之一，在实际应用中会涉及到高阶的移动平均，致使参数估计困难，限制了其实际应用。Bollerslev[2]在1986年对ARCH模型进行了推广，提出了广义自回归条件异方差（Generalized Autoregressive Conditional Heteroskedastic Model，GARCH）模型，放松了对系数的限制。在此基础上，衍生出许多GARCH模型，例如TGARCH、EGARCH、IGARCH等，这些模型已被普遍应用于股票、汇率和利率等数据的研究。除了这些领域的应用以外，GARCH类模型在管理科学与工程领域也有相应的应用，如预测瓦斯浓度、预测城际高铁客流量、构造控制图、分析贝叶斯局部影响等。由此可见，GARCH类模型的应用领域十分广泛。

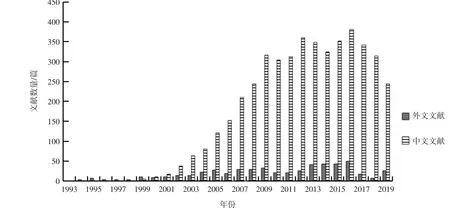
图1 GARCH模型中文文献和外文文献发表数量图

此外，本文统计了1993—2019年来国内外关于GARCH模型的年度发文数量，如图1所示。该图显示了关于GARCH模型的中文文献和外文文献的年度发表数量，从图中可以很明显地看出：（1）对GARCH模型的研究国外要早于国内，且在早期阶段，关于GARCH模型的文献数量较少；（2）从2001年开始，国内外每年发表的文章数量大致呈增长趋势，但国内增长趋势比较明显，这表明对GARCH模型的研究日益广泛。

1 基本的ARCH和GARCH模型

Engle（1982）[1]将自回归条件异方差（ARCH）模型，表示为式（1）：

式（1）被称为 ARCH（q）模型，它充分显示了模型残差所具有的条件异方差性。

ARCH模型的提出很好地刻画了金融时间序列波动性集群的特点，但如前所述，其滞后阶数q往往较大，这导致了对参数的过多要求，因为必须保证方差为正，而用实际数据估计出的模型往往不能满足这一要求。Bollerslev（1986）[2]对 ARCH 模型进行了推广，提出了广义自回归条件异方差（GARCH）模型，模型的一般表达式为式（2）：

式（2）被称为 GARCH（p，q）模型，其中独立同分布，且E（vt）=0，Var（vt）=1。

GARCH模型同时考虑了自回归和异方差中的移动平均成分，从形式上看，一个高阶的ARCH模型可能有一个更为简洁且更易识别和估算的GARCH表达式。显然，GARCH模型比较简洁，与ARCH模型相比对系数的限制较少。GARCH模型自提出至今是最常用、最可行的异方差序列拟合模型。

2 拓展的GARCH模型族

虽然与ARCH模型相比，GARCH模型具有一定的优势，但从GARCH模型的表达式可知，参数的约束条件比较严格，即无条件方差非负和条件方差平稳。同时，GARCH模型忽视了正负扰动的非对称性，这些不足在一定程度上限制了GARCH模型在某些领域的应用，由此衍生出了各种各样的GARCH类模型。

2.1 反映非对称性的相关模型

GARCH模型中由于条件方差对正面冲击与负面冲击带来的反应一致，而在股票市场上，利好消息与利空消息对股票市场的影响并不一样。因此学者们通过改进基本的GARCH来反应这一非对称效应。

Zakoian（1994）[3]在方差方程中引入虚拟变量来反应非对称效应，即TGARCH模型。TGARCH模型以区分均值方程扰动项为条件，在波动方程中加入了虚拟变量来检验波动性，模型的一般表达式为式（3）：

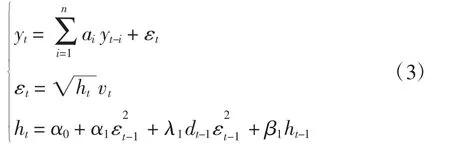
式（3）中，λ1是非对称系数（见表 1），dt-1是虚拟变量，当 εt-1＜ 0 时，dt-1=0，当 εt-1≥0 时，dt-1=0。只要虚拟变量前的参数不等于0，利好消息与利空消息对波动率的影响就是非对称的。

另一种信息不对称影响的模型是指数GARCH模型（EGARCH 模型），该模型由 Nelson（1991）[4]提出，模型中用ln（ht）来代替ht，同时引进加权扰动函数。通过这一改进，使得可正可负，不需要对模型中参数加以任何限制，使得ln（ht）估计参数更为方便，模型的一般表达式为式（4）：

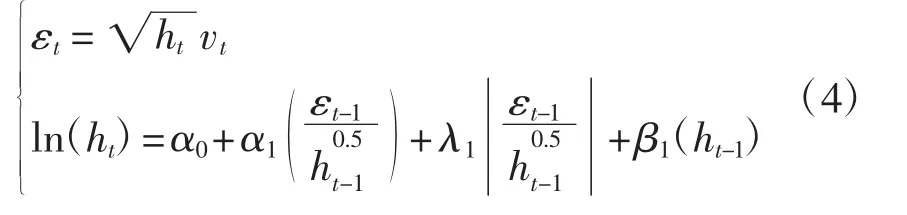
式（4）中，λ1是非对称系数（见表 1）。EGARCH模型可以允许系数为负，且考虑了杠杆效应，但相对于TGARCH模型，很难预测条件方差。

表1 非对称系数

此后，Ding等（1993）[5]还将标准离差引入方差方程，建立了非对称幂GARCH模型，即APGARCH模型。APGARCH模型具有一般GARCH模型的特点，仅多了两个参数，比GARCH模型具有更大的灵活性。

Engle 和 Ng（1993）[6]认为，金融市场上的某些数据存在非线性特征，若忽略这个特征将会降低模型拟合的精确度，因此提出了非线性非对称的GARCH模型，即NAGARCH模型。

以上非对称模型均假定扰动项服从正态分布，但有些数据并没有明显的正态分布特征，针对这一问题，Sentana（1995）[7]提出了二次 GARCH 模型，即QGARCH模型，该模型可以处理具有偏度（正的或负的）分布的数据。

2.2 反映高频、混频数据信息的相关模型

传统GARCH模型针对低频数据即对日、周、月、季度或者年度数据进行分析，低频数据容易造成信息的缺失，而“已实现”波动率可以对高频数据即日内数据，是指以小时、分钟或秒为采集频率的数据进行度量，为此，将“已实现”波动率与GARCH模型相结合成为学者们研究的重点。

Engle（2002）[8]直接将“已实现”波动率作为外生变量与GARCH模型巧妙结合起来，提出了GARCH-X模型，使得该模型具有更好的样本外预测能力和模型解释能力。由于GARCH-X模型直接将“已实现”波动率作为一个外生变量加入方程，不能解释“已实现”波动率的变动，模型存在一定局限性。

Hansen 等（2012）[9]将基于高频数据的“已实现”测度与GARCH模型相结合，简单地实现了条件方差和“已实现”测度的联合模型。以Realized GARCH（1，1）为例，模型的一般表达式如式（5）：

其中，vt～（0，1），ut～（0，）。rt是对数收益率，φt是已实现测度。

Hansen 和 Huang（2016）[10]在 Realized GARCH模型的基础上，添加多个“已实现”波动率，并在波动率方程中添加杠杆函数，即Realized EGARCH模型。该模型不但可以同时对多个“已实现”波动率进行刻画，而且还反映了历史误差项对当前收益率波动的非对称影响。

由于Realized GARCH模型不能反映残差在方向上对未来资产收益的冲击，魏正元等（2017）[11]在Realized GARCH模型中的已实现测度方程中引入参数的扰动，提出了Realized NGARCH模型，该模型可以描述过去已实现测度对当前收益波动大小可能做出的冲击。

在大部分研究中，同一个模型内使用的数据是相同频率的，但也经常会遇到频率不同的数据，因而Engle等（2013）[12]提出了混频数据模型，即GARCHMIDAS模型，模型的一般表达式可参考苏治等[13]一文。该模型可以混合不同频率的数据，利用了更多数据的信息，具有较高的估计精度。

2.3 多元GARCH拓展模型

在金融市场上，其波动率的研究取得了很大的进展，但金融市场的资产多种多样，在进行金融资产组合投资时，就会面临多资产、多收益、多风险的问题。同时，在经济全球化背景下，各国金融市场互相联系、互相影响。研究股票市场之间的联动性，不仅对于个人投资者、机构投资者进行风险管理有较大的参考意义，而且对于政府在金融监管及股票市场政策的制定也有较大的参考价值。鉴于此，许多学者在GARCH模型的基础上进行改进和扩展，形成了一系列的多元GARCH模型。

Bollerslev 等（1988）[14]建立了 VECH-GARCH模型，利用对角矩阵来研究多变量的波动过程。由于VECH-GARCH模型中的协方差矩阵不能保证其为正定矩阵，在VECH-GARCH模型的基础上，Engle 和 Kroner（1995）[15]提出了 BEKK-GARCH 模型，主要目的是为了保证估计出来的协方差矩阵是正定矩阵，且模型中参数更易估计。

虽然BEKK-GARCH模型中的参数更易估计，但需要估计的参数过多，且模型中的参数没有明确的经济意义解释，Bollerslev（1990）[16]提出不直接对协方差矩阵进行建模，而是对相关系数矩阵进行建模，即常数条件相关广义自回归条件异方差（Constant Conditional Correlation GARCH，CCC-GARCH）模型。该模型不仅涵盖了单变量模型的波动特性，而且可以刻画不同变量间的相关系数。

在建立CCC-GARCH模型的时候，假定各个序列之间的相关系数为常数，但实际情况中，金融时间序列之间的相关系数并不是常数，使得CCCGARCH模型不能捕捉序列之间的动态相关性。因此，Engle等（2001）[17]在此基础上引入动态条件相关多变量广义自回归条件异方差（Dynamic ConditionalCorrelation Multivariate GARCH，DCC -GARCH）模型，它不仅能捕捉跨市场的波动溢出效应，还能捕捉各种资产之间的风险交叉传递，DCCGARCH模型的一般表达式为式（6）：

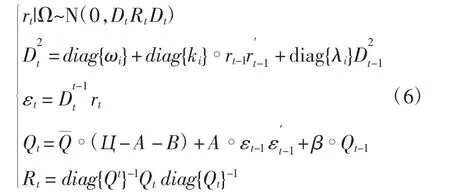
式（6）中，Ω为所有信息的集合，rt为N×1维收益向量，Dt为两个收益序列的相关系数对角矩阵，Qt为条件协方差矩阵，Rt为动态条件系数相关矩阵，εt是残差λ为指数平滑系数，为Hadamard积，A，B为模型参数矩阵。

以上这些常用的多元GARCH模型在估计时技术成本太高，存在“维数灾难”问题，因此Burns（2009）[18]对模型进行改进，提出了PC-GARCH模型。该模型减少了计算量，可以更好地拟合数据，使相关估计更加稳定。

2.4 其他拓展模型

除了上述相关方面的拓展之外，许多学者发现ARCH模型扰动项的自相关系数呈典型的双曲率衰减特征，引发了ARCH模型与长记忆模型相结合的研究。

利用GARCH模型建模时，若外部冲击带来的影响衰减缓慢，即条件方差序列存在冲击影响的持续记忆性，则表现为估计的GARCH系数与ARCH系数之和将无限趋近于1，甚至略大于1，此时条件方差序列是非平稳的，Engle和 Bollerslev（1986）[19]借助差方方程，对GARCH模型重新整合得到单整GARCH（IGARCH）模型。该模型介于短记忆GARCH模型与长记忆GARCH模型之间，是经济、金融时间序列波动持续性研究的基础。

Baillie等（1996）[20]提出了 FIGARCH 模型，与传统GARCH模型相比，该模型对于具有长记忆性的金融变量序列拟合效果更加显著。Bollerslev和Mikkelsen（1996）[21]在 FIGARCH 模型的基础上引入杠杆系数，提出了FIEGARCH模型，该模型通过对数形式处理条件方差，可以确保条件方差为正值。Davidson（2004）[22]认为 FIGARCH 模型存在一定的缺陷，FIGARCH模型中的记忆参数与分整形式中参数的作用相反，造成了很难对记忆参数进行解释，因此Davidson[22]将FIGARCH模型扩展为HYGARCH模型，用双曲GARCH模型来描述序列的长记忆特征，使得该模型能同时捕获波动聚类和长记忆性两种典型特征。

此外，考虑到在金融市场上风险厌恶的投资者会在持有风险资产时要求相应的风险补偿，而这一风险可以用资产收益的波动来衡量，Engle等（1987）[23]把风险引入均值方程中，即ARCH-M模型和GARCH-M模型。在此基础上，又有学者提出了TGARCH-M模型和EGARCH-M模型。此类模型又被称为均值GARCH模型，即条件均值依赖于条件方差，更好地拟合了股市收益。

经典GARCH模型有效地刻画了很多领域时间序列的波动性，但由于经典GARCH模型以条件方差为中心构建方差方程，难以和某些实际数据契合。因此，Schwert（1989）[24]使用条件标准差来构建方差方程，即TSGARCH模型，提高了模型中参数估计的效率。

3GARCH模型的应用

本文主要统计了10个应用领域，分别是金融、宏观经济管理与可持续发展、投资、证券、数学、市场研究与信息、贸易经济、工业经济、农业经济和石油天然气工业，如图2所示。从图中可以看出，GARCH模型在金融领域的研究占比最大，其次是宏观经济管理与可持续发展领域和投资领域。因此基于以上模型的简单介绍，本文选择占比最大金融领域来研究GARCH模型族的应用，并且选择几篇具有代表的文献来介绍其应用。

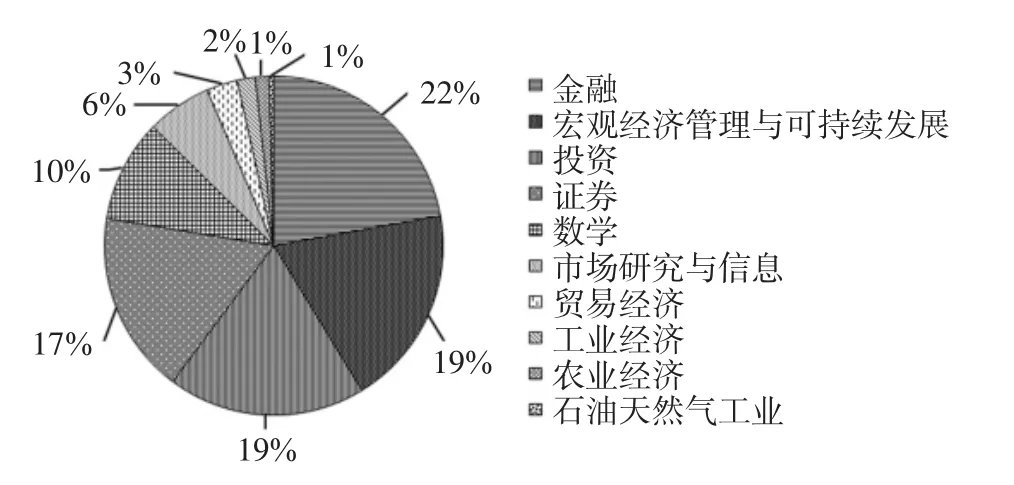
图2 GARCH模型的研究领域分布图（2019年）

3.1 在股票市场预测上的应用

在股票市场方面，Basel等（2005）[25]研究了不同GARCH模型的样本预测能力，发现在信息对称时，GARCH（2，1）模型对 S＆P500 的波动性描述更为准确。Pagan等（1990）[26]对波动率的研究也表明，GARCH模型拥有良好的的拟合效果和预测精度。Prateek等（2016）[27]比较了最近提出的Realized GARCH模型与GARCH模型、EGARCH模型在预测股票市场波动性的预测能力。文中选用16个国际股票指数为研究对象，发现若使用QLIKE损失函数，Realized GARCH模型的预测能力优于EGARCH模型。Eric等（2013）[28]使用 GARCH-MIDAS模型，利用宏观经济变量的月度数据，证明了中国股票市场拥有投机特征的假定，同时说明了宏观经济方面在股票市场的波动性中发挥了越来越大的作用，尤其是CPI通货膨胀。

国内学者唐齐鸣和陈健（2001）[29]研究了中国股市的ARCH效应，通过实证发现ARCH类模型能较好地刻画我国股票市场的波动性。杨琦和曹显兵（2016）[30]运用ARMA-GARCH模型对深圳A股大众公用的股票价格进行了分析预测。文中使用GARCH（1，1）模型进行估计，有效地捕捉了模型残差中存在的条件异方差性，在进行预测时发现该模型在短期内有较好的预测能力，但若使用该模型对股票的价格进行长期预测，预测效果会大幅下降。郑挺国和尚玉皇（2014）[31]进一步使用混频抽样GARCH-MIDAS模型研究发现一系列宏观经济变量（如宏观经济环境、失业率、经济景气指数等）会对股市波动产生的显著影响，而GARCH-MIDAS模型的估计结果优于基本的GARCH模型，说明GARCH-MIDAS模型比较适合刻画中国股市波动率。

3.2 对波动的非对称效应的研究

在波动非对称效应方面，Danielson（1994）[32]以S＆P500指数的日数据为研究对象，发现EGARCH（2，1）模型比 ARCH（5）、GARCH（1，2）模型更好地拟合了数据。Sabiruzzaman等（2010）[33]认为除了考虑对股票价格波动率进行建模，还要考虑对交易量波动进行建模，交易量在金融市场中起着关键作用。文中研究了香港证券交易所日交易量指数波动的模式，利用GARCH模型和TGARCH模型对交易量的波动性进行模拟，发现GARCH和TGARCH模型都很好地拟合了数据。然而，TGARCH模型能够分离好消息和坏消息的影响，还发现每日交易量具有明显的杠杆效应，说明TGARH模型更适合于对交易量指数的波动率进行建模。

国内学者潘锡泉（2017）[34]采用EGARCH模型对人民币汇率波动序列的非对称性进行了研究，发现人民币第二次汇率制度改革之后存在着明显的杠杆效应，而人民币第二次汇率制度改革之后的杠杆效应不显著。朱婧等（2015）[35]认为杠杆效应会扩大风险的损失，故将测量风险的VaR模型与非对称GARCH模型相结合，以上证综合指数和深证成份指数为分析对象，分别对其建立模型。结果发现EGARCH（1，1）模型能较好地拟合上证综合指数，而TGARCH（1，1）模型能较好地拟合深证成份指数，这说明两个数据样本均具有杠杆效应。

3.3 关于市场联动分析的研究

在市场之间联动性分析方面，Sibel（2012）[36]认为金融传染对货币政策、风险计量、资产定价和投资组合分配都很重要，因此研究美国次贷危机期间对新兴市场的影响十分必要。采用DCC-GARCH模型来检验美国次贷危机期间外汇市场之间金融传染的存在，该模型比其他方法具有一定的优势。研究发现美国次贷危机期间大多数发达国家和新兴国家都存在着传染，但新兴市场似乎受到美国次贷危机蔓延的影响最大。Yang 和 Steven（2016）[37]通过研究标准普尔500指数和沪深300指数期货市场之间的相互依赖性来说明中国股市及其对其他股票市场的影响。利用DCC-GARCH模型进行实证分析，结果表明美国指数期货市场在美国和中国指数期货市场之间的信息传递过程中占据主导地位，美国和中国指数期货市场之间的相关性取决于过去的信息，当负面冲击到达两个市场时，相关性就会提高。

国内学者李小好和蔡幸（2019）[38]利用DCCGARCH模型讨论了中国与东盟股票市场之间的一体化进程，发现近些年股票市场一体化进程有了明显提高。李竹薇等（2018）[39]采用DCC-GARCH模型对APEC中12个主要成员国的股票市场为研究对象，发现股票市场存在着很强的联动效应，并且这种联动性具有时变性。

4 比较与总结

综上所述，有必要对本文所介绍的各种模型的优缺点进行比较，整理结果如表2所示。

从表2可以看出，各个模型在某些方面具有独特的优势，但也存在着一些不足。在如此多的模型中，如何选择一个合适的模型或者在多个合适的模型中如何选择最理想的模型显得至关重要。因此，我们要根据实际情况选择恰当的模型，才能达到事半功倍的效果。

本文系统地总结了ARCH模型体系的发展及其相关应用，并详细介绍了一些重要模型。自从Engle提出ARCH模型以后，各种拓展模型及应用成果不断出现，从ARCH模型到GARCH模型，从对称GARCH模型到非对称GARCH模型，从线性ARCH模型到非线性GARCH模型，从短记忆GARCH模型到长记忆GARCH模型，从平稳GARCH模型到单整GARCH模型，从一元GARCH模型到多元GARCH模型，从低频GARCH模型到高频GARCH模型以至混频GARCH模型，这些发展说明GARCH模型体系日趋完善。GARCH模型族能够在几十年内发展为现代经济计量学一个重要的领域，与其运用领域的广泛性密不可分。如前所述，GARCH模型族在金融市场中的实际应用极其普遍和广泛，为投资机构、监管机构、政府机构等实际金融风险管理提供了有益建议。在未来无论是理论上还是应用上，GARCH模型族仍有进一步发展的空间，例如在理论上将不同维度上的模型进行融合发展，并进一步指导对现实金融问题的研究。

表2 各种模型的优缺点比较