基于VTI介质的隧道超前探测qP波正演模拟研究

董载天 王军民

摘      要： 由于隧道超前探测的环境与常规石油地震勘探的差异，不宜直接将过去的模拟方法拿到隧道中进行应用。结合层状地层表现出横向各向同性的特性，推导出在隧道空间适用的二维VTI介质一阶qP波方程，分析了其稳定条件。建立断层和软弱夹层的几种数值模型，利用PML边界解决模型边界反射，采用交错网格进行有限差分正演模拟，得到其共炮点道集。结果表明，qP波有限差分法可以快速地模拟不良的地震响应，规避伪S波和数值不稳定问题，为隧道超前探测资料的解释提供依据，提高预测的准确性。

关  键  词：隧道超前探测;VTI介质;qP波;PML

中图分类号：TV221.2       文献标识码： A       文章编号： 1671-0460（2020）03-0683-07

Forward Modeling of Tunnel Advanced

Detection qP Wave Based on VTI Medium

DONG Zai-tian， WANG Jun-min

（Yangtze University， Hubei Wuhan 430100， China）

Abstract：  Due to the difference between the environment of tunnel pre-detection and conventional petroleum seismic exploration， it is not appropriate to directly apply the past simulation method to the tunnel. Combined with the transverse isotropy characteristic of layered stratum， the first-order qP wave equation of the two-dimensional VTI medium suitable for tunnel space was derived， and the stability conditions were analyzed. Several numerical models of fault and weak interlayer were established. The boundary reflection of the model was solved by PML boundary， and the finite difference forward modeling was carried out by staggered grid to obtain the common shot gather. The results show that the qP wave finite difference method can quickly simulate the bad seismic response， avoid the pseudo S wave and numerical instability problem， and provide a basis for the interpretation of tunnel advance detection data to improve the accuracy of prediction.

Key words：  tunnel advance detection;  TI media;  qP wave;  PML

在我国经济高速发展的当下，大量公路铁路工程都有隧道施工。在隧道工程施工过程中，由于掌子面前方地质状况不详，面对破碎带、裂隙和溶洞的支护不当或支护不及时，经常出现坍塌、突水突泥、冒顶等重大灾害，造成严重的人员伤亡和财产损失。显然在隧道工程中，使用超前探測技术了解掌子面前方地质状况，对工程施工安全极其重要。超前探测方法从原理上可以划分为：地震波法、电磁法（瞬变电磁、电阻率、激发极化、核磁共振）、岩体温度法等，其中地震波法在远距离勘探中有较好的分辨率，成为目前隧道超前探测中的常用方法之一。在隧道地震波法探测中，常用的方法有VSP、HSP^[1]、TSP^[2]、TVSP^[3]、陆地声纳^[4]、HSP^[5]、TRT^[6，7]、TST^[8]、ISIS^[9]等方法。由于隧道施工现场的空间狭小且工程工期压力大，所以隧道超前探测技术必须满足狭小场地条件下进行大距离、高精度、高效率探测要求^[10]，这就要求在对传统方法技术（测线与探测对象平行）进行改进（测线与探测对象垂直）的同时，进一步研究地震波在隧道复杂条件下的传播机理特性^[11]。因此，本文在层状地层条件下，构建断层、软弱夹层等不良地质灾害体模型，从一阶速度?应力qP波方程出发，采用交错网格高阶有限差分进行隧道复杂波场的正演模拟计算，以充分认识不同条件下地震波响应特征。

1  TI介质的波动方程

在我国，层状地层分布广泛，约占陆地面积的77.3%^[12]，在隧道施工过程中大多要面对这样的地质环境，而地下层状在横向各向同性地层往往表现出横向各向同性的物理响应特征。介于笔者使用波动方程法进行地震数值模拟，所以推导出横向各向同性（TransverseIsotropy）介质的波动方程尤为重要。

1.1  波动方程导出

波动方程的建立涉及应力、应变和位移这三个物理量，需要使用弹性体的本构方程、运动微分方程和柯西方程。由本构方程，可知弹性体应力与应变关系表达式：

        （1）

式中： — 应力张量;

e — 应变张量;

C — 弹性常数。

弹性常数共有81个，由柯西方程可知，应变张量有对称性：

               （2）

其中：u、v —位移分量;

x， y —笛卡尔坐标。

而应力张量也有此种对称性，即。因此弹性常数减少为36个，同时弹性常数张量相对于主对角线对称，有。使用单下标替代双下标11→1，22→2，33→3，23（32）→4，13（31）→5，12（21）→6，则可的表达式：

      （3）

上式可简记为：

             （4）

从弹性体的角度，描述完应变与应力关系、应变与位移关系后，通过牛顿第二定律可建立运动平衡微分方程：

              （5）

式中：— 彈性体密度，kg/m;

U — 位移张量;

— 应力张量;

t — 时间，s;

F —体力张量;

L —偏导算子。

偏导算子L为：

       （6）

利用Cauchy方程可将（5）式表达为：

         （7）

1.2  TI介质中qP波波动方程

地表岩土物理性质极其复杂不便于数值模拟研究，地球物理学家为了能借助波动物理研究其波传播特性，根据各项异性弹性体介质的基本对称性进行了分类。其中三方、六方各项异性介质常叫做横向各向同性（Transverse Isotropy，简称TI）介质，是目前实际应用研究中使用最广泛的模型。TI介质又根据对称轴的水平和垂直细分为，VTI介质和HTI介质（图1）。

两介质都需要5个独立的弹性参数来描述，其弹性矩阵分别为：

分别将两式带入公式（7），可得VTI介质三维波动方程：

由于VTI介质与地下实际介质的响应特质较为一致且研究最为广泛，所以笔者主要使用VTI介质的弹性波波动方程，因此此处不再给出HTI介質的波动方程。

在利用此方程进行TI介质的弹性波正演模拟中，波动方程的包含三个分量，占用计算机大量内存，同时由于纵波速度快于横波，而网格的空间步长和采样时间步长主要受最波的小速度影响，为稳定计算，只能减小空间和采样的间隔，使得计算的时间点数与空间点数大幅提高，进一步减慢了计算速度，不利于计算机模拟。且目前实际勘探仍以纵波为主，多分量数据中进行横波分离仍然是个难点问题。

因此笔者借用Alkhalifah提出的声学假设条件，直接将横波速度设为零，从而在复杂的 VTI 介质弹性波方程中分裂出qP波方程^[14]。该方程不产生横波，虽然现实中上不可实现，但在运动学上能对弹性波方程进行有效地近似，便于研究TI介质中qP波的传播规律。

根据Alkhalifah的假设导出的三维 VTI 介质中的qP波方程为：

   （11）

式中：F — 为波场函数;

t — 为时间，s;

x、y、z — 为三维空间坐标;

v 、v_v — qP波的动校正速度和垂向速度，m/s;

η — 各向异性参数。

已知：e、d 为 Thomsen 参数^[15]。

由于隧道超前探测观测方向为掌子面正前方，而常规地震勘探观测方向为地面垂向（如图2），所以笔者后面推导VTI介质中的波动方程时只保留xy分量。

因此，由式（11）可得二维VTI介质中qP波方程：

直接求解上式需要消耗大量内存和时间，所以利用，可将上式转化为：

其中为应力。借鉴Hestholm推导二维VTI介质中qP波方程的一阶应力-速度方程形式的方法，可得：

式中：— 弹性体密度，kg/m;

v_x、v _y— x、y方向速度，m/s;

 — 计算过程中的中间变量。

2  交错网格

在实际计算过程中必须对介质模型进行离散，将介质模型网格化。实际应用过程中，交错网格相比规则网格有更好的差分算子局部特性，更高的精度和更好的收敛性。所以笔者采用交错网格（如图3）将放置在网格节点。

利用Taylor级数展开法，用网格节点上数值的差商近似代替前式中的导数。推导出了时间域 2 阶、空间域2N阶精度的交错网格离散差分格式。

式中： — 空间间隔，m;

— 时间间隔，s;

i、j、k— 空间和时间节点;

U、V— 速度分量v_x和v_y的离散值，m/s;

P、Q、R— 应力和的离散值。

3  有限差分模拟中的重要问题

3.1  PML边界条件

针对隧道超前探测的弹性波数值模拟而设计的数据模型，仅考虑深埋隧道时，隧道空间为自由边界，计算区域外部边界则都是人工截断边界。人工边界会使向外传播的弹性波完全反射回去，从而使正演模拟计算结果与实际情况大不符。为了尽量降低人工截断边界所产生的影响，引入Berenger针对电磁波传播提出了完美匹配层（Perfect Matched Layer，简称 PML）吸收边界条件，削弱人工截断边界的反射，改善正演模拟效果。

根据PML的推导思路，可给出式（14）的吸收边界方程：

式中：d（x）、d（y） — 阻尼因子;

R — 反射系数;

 — 完美匹配层吸收边界的厚度，m;

h — 完美匹配层吸收边界的深度，m;

v — 匹配层中的弹性波波速，m/s。

3.2  稳定性

波动方程的差分格式按照时间进行递推，前一时刻的波函数数值解的舍入误差必然会对下一时刻的波场产生影响。这就需要对误差传播情况进行估计，使其不会随着时间推移而快速增长，以致影响数值模拟的效果进而破坏计算，使模拟无法继续进行。笔者此处借鉴Virieux在1986年提出的推导方法，得到二维VTI介质中二阶时间差分精度、2N阶空间差分精度的稳定条件：

      （17）

当中表示模型中最大速度的平方。当模型横纵空间步长一致时，亦可将方程改写为：

             （18）

3.3  震源加载

此部分还有一个重要问题就是加载震源。本文为保证成像的分辨率，选择使用零相位雷克子波作为震源。其时间域表达形式为：

        （19）

式中：t₀ —初始时刻，ms;

f —主频， Hz。

4  数值模拟实例

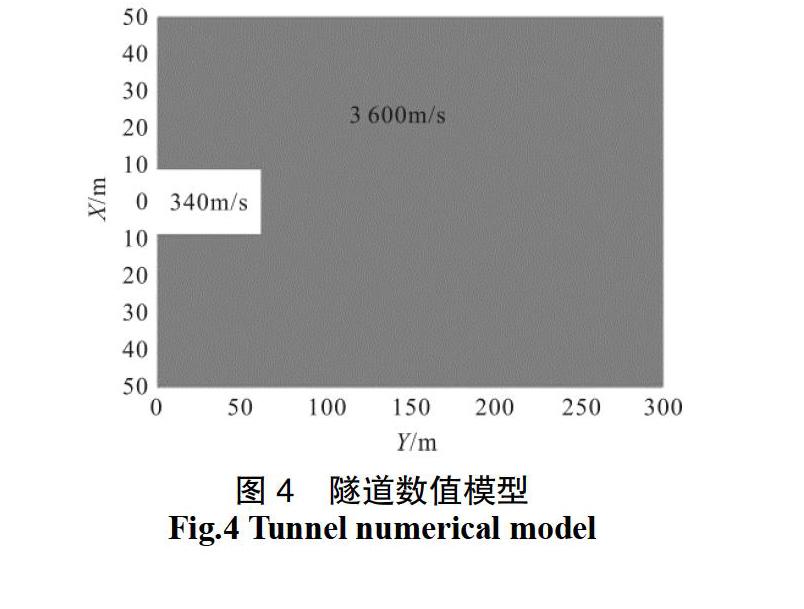
建立隧道空间的模型（如图4），正演模型的尺寸为300 m×100 m，模型四周使用PML吸收边界。

隧道尺寸为60 m×8 m，空腔中充填空气，波速340 m/s; 围岩波速3 600 m/s。采样间隔为0.2 ms，采样时长为0.1 s。

观测方式如所示，掌子面中心单震源，左右两侧墙壁各布置4个检波器，间隔2 m，水平最小炮间距10 m。震源与检波器皆置于墙内，埋深2 m。

通过正演模拟可得到地震响应记录（图6），为共炮点道集（CSP）。可以看出直达波能量很强，无边界反射和伪S波干扰。根据费马原理计算的初至时间在4 ms左右，基本与记录吻合。

4.1  不良地質体模型及其地震响应

隧道施工过程中会遇到很多危害施工安全的不良地质体，常见的有：断层破碎带、软弱夹层等。由于二维平面不存在倾角，所以后续模型中需要关注不良地质体的走向。

4.1.1  断层模型及响应

斷层破碎带是由于断层上下盘搓动引起断面附近的岩体发生破碎，形成破碎带。其稳定性较差，容易引发隧道塌方;在地下水富集区域，破碎带变成了一条良好水通道，极易引发突水突泥灾害。由于破碎带与断层的伴生特性且破碎带本身理化性质过于复杂，笔者此处将断层破碎带的模型设置为断面两侧阻抗不同，破碎带并不在模型当中直接体现。数值模型构建时，首先选择走向与隧道方向垂直，距掌子面80和120 m的断层，断层右盘波速为4 000 m/s（图7）。

对比两模型的CSP道集（如图8）可以看出，当断面与掌子面距离减小时，阻抗界面的反射波逐渐靠近强振幅的直达波，初至有可能被遮蔽，此时仅靠时域记录是难以判断前方断面距离的;当两者间距拉大，反射波整体向后时移，初至明显但振幅减弱，现场施工噪音较强时，会难以见到完整波形。

4.1.2  软弱夹层及响应

软弱夹层成因复杂且尚无统一的分类原则，此处只针对沉积型软弱夹层进行分析。此种软弱夹层往往形成与河流沉积环境，层中粉砂岩、泥岩含量偏高，强度低质地较软弱^[17]。当构造作用使夹层被剪切、破碎时，无论区域是否富水，都会产生低速低密度的软弱夹层。软弱夹层的数值模型参考断层模型，将夹层设置在掌子面前方80 m处且走向与隧道方向垂直，此时一次反射波不会被直达波遮蔽。分别构建10、20 m厚的夹层，波速为800 m/s（如图9）。

此时获得CSP道集（如图10）。由于此时夹层与围岩阻抗差异过大，且检波器内置在墙壁中，导致阻抗界面反射波振幅较强。对于薄夹层来说，子波在夹层中旅行时较短，夹层右侧依旧为高阻抗差界面，所以10 m薄夹层的地震反射记录上出现多次波。而层厚为20 m的夹层，子波旅行时被拉长此时反射波没有在记录时间内返回到检波器，故道集上无明显反射波。

将软弱夹层与掌子面之间距离拉大至120 m（模型如图11）。

从两模型CSP道集（如图12）可以看出，此时两种模型的地震响应颇为一致，显然夹层右界面的反射波由于旅行时较长没有在记录时长内返回到检波器位置。

构建一个右盘为低速岩体的断层（如图13），此时获得其CSP道集（如图14），其与掌子面距离为120 m的软弱夹层的地震响应基本一致。可见固定采样时长有时无法分辨的不同的不良地质体，此时需要增加采样时长或者利用其他地质勘探资料来确定不良地质体形态。

5  结 论

隧道超前探测尚处于发展阶段，由于其探测空间的复杂以及其与传统地震勘探的差异，使得隧道超前探测在实际应用过程中存在一些问题。笔者从弹性体基本理论出发，逐步推导出适用于隧道超前探测二维正演模拟公式，并模拟了断层、软弱夹层的地震响应。从中得到一些结论：

（1）利用三维VTI介质波动方程，根据隧道超前探测的观测方式，推出了适用于隧道勘探正演模拟的二维VTI介质qP方程，后导出其1阶应力-速度方程，进行时间2阶空间2N阶的有限差分正演模拟。其计算迅速，规避了伪S波干扰和计算不稳定性，便于快速得到不同地质模型的地震响应特征。

（2）利用PML吸收边界，处理了隧道后方人工边界引起的反射。采用交错网格和，使方程能较好地模拟断层和软弱夹层的地震响应，减少频散。

（3）二维平面模拟中，采样时长与断层、软弱夹层的物性参数组合不当，会导致两种不同的不良地质体产生相同的地震响应。在数值模拟时，可改变模型参数，使其显现不同的地震响应。而在现场实际情况来说，需要现场工程师结合其他地质勘探资料综合分析。

参考文献：

[1]柳杨春. HSP地质超前预报技术及其应用[J]. 西部探矿工程， 1997 （05）： 40-42.

[2]刘志刚， 刘秀峰. TSP（隧道地震勘探）在隧道隧洞超前预报中的应用与发展[J]. 岩石力学与工程学报， 2003， 22 （8）： 1399-1402.

[3]曾昭璜. 隧道地震反射法超前预报[J]. 地球物理学报， 1994 （2）.

[4]钟世航. 陆地声纳法的原理及其在铁路地质勘测和隧道施工中的应用[J]. 中国铁道科学， 1995 （4）： 48-55.

[5]Inazaki T， Isahai H， Kawamura S， et al. Stepwise application of horizontal seismic profiling for tunnel prediction ahead of the face[J]. The Leading Edge， 1999， 18（12）： 1429?1431.

[6]Otto R， Button E， Bretterebner H， Schwab P.The application of TRT-trae reflection tomography-at the Unterwald Tunnel[J]. Geophysics， 2002， 20 （2）： 51-56.

[7]Yamamoto T， Shirasagi S， Yokota Y， Koizumi Y. Imaging geological conditions ahead of a tunnel face using three-dimensional seismic reflector tracing system[J]. International Journal of the JCRM， 2011， 6（1）： 23-31.

[8]赵永贵. TST隧道超前预报技术及应用[C].中国地球物理学会第22届年会论文集，2006.

[9]Borm G， Giese R， Klose C， et al. ISIS integrated seismic imaging system for the geologic prediction ahead in underground construction[C].65th Annual Conference and Exhibition， EAGE， Extended Abstracts. Norway， 2003： 887?899.

[10]宋先海， 顾汉明， 肖柏勋. 我国隧道地质超前预报技术述评[J]. 地球物理学进展， 2006 （02）： 605-613.

[11]张平松，吴健生.中国隧道及井巷地震波法超前探测技术研究分析[J]. 地球科学进展， 2006 （10）： 1033-1038.

[12]张学民. 岩石材料各向异性特征及其对隧道围岩稳定性影响研究[D]. 中南大学， 2007.

[13]程玖兵， 康玮， 王腾飞. 各向异性介质qP波传播描述Ⅰ： 伪纯模式波动方程[J]. 地球物理学报， 2013， 56 （10）： 3474-3486.

[14]Alkhalifah， Tariq. An acoustic wave equation for anisotropic media[J]. Geophysics， 2000， 65（4）： 44-48.

[15]Thomsen， Leon. Weak Elastic Anisotropy[J]. Geophysics， 1986， 51：1954-1966.

[16]Clayton R， Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bull. seismol. soc. amer， 1977， 67 （6）： 1529-1540.

[17]胡涛，任光明，聂德鑫， 等. 沉积型软弱夹层成因及强度特征[J]. 中国地质灾害与防治学报，2004， 15 （1）： 124-128.