例析多元最值问题的常规求解方法

广东省惠州市第一中学 (516007) 方志平

多元最值问题是指含有多个变量、以求解最大值或最小值为目的的一类数学问题.这类问题内涵丰富,知识面广,综合性强,形式不拘一格,解法灵活多变.多元函数最值问题的难点就在于变量多，导致学生处理问题相对麻烦，所以在解决此类问题时常需将变量数减少，从而降低解题的难度.下面将举例分析求解有关多元最值问题的一些常规方法,供读者参考.

1.基本不等式法

例1 (2016年全国高中数学联赛广东省预赛试题)若正数x、y满足x+3y=5xy,则3x+4y的最小值是.

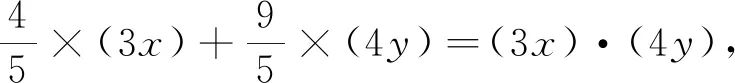
2.消元法

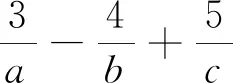
评注：消元是处理多元函数最值问题最基本的方法，遇到此类问题，首选方法就是消元法.如果能够消元，就可以化多为少，化难为易，从而使问题得到解决.

3.分离变量法

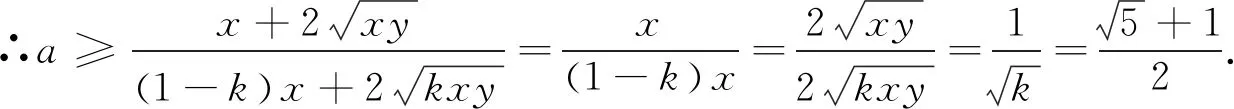
4.判别式法

例4 (2017年全国高中数学联赛吉林省预赛试题)已知x,y,z∈Z,且x+y+z=3,x3+y3+z3=3,则x2+y2+z2=.

当z=1时，(x,y,z)=(1,1,1)；

当z=4时，(x,y,z)=(-5,4,4),(4,-5,4)；

当z=-5时，(x,y,z)=(4,4,-5).

综上，x2+y2+z2=3或57.

评注：题中条件是两个等式，三个变量，方程的解一般是不确定的.不妨用z表示x+y,xy构造一元二次方程，由于方程有整数根x、y，所以判别式Δ为完全平方数，从而先求出整数z的值，于是帮助我们找到了问题解决的突破口.

5.代换法

例5 (2016年全国高中数学联赛四川省预赛试题)实数x、y、z、w满足x+y+z+w=1,则M=xw+2yw+3xy+3zw+4xz+5yz的最大值是.

评注：本题的条件很有隐蔽性，难点在于将M=xw+2yw+3xy+3zw+4xz+5yz合理分组、分解，上述整理具有一定的创造性，将条件x+y+z+w=1代换，把四元变为三元，给问题的解决带来了转机.

6.引入参数法

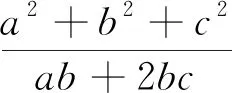
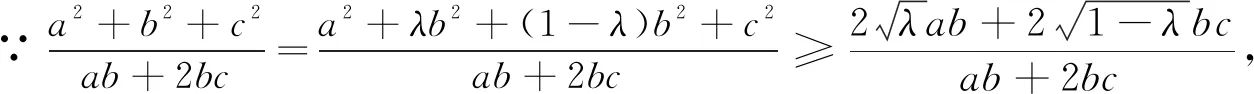
评注：观察分子、分母结构特征，需将分子中的b2分成两部分，即λb2+(1-λ)b2,再利用基本不等式，注意取等条件，问题则迎刃而解.本题与例3在解法上是同出一辙的.

7.换元法

例7 (2017年全国高中数学联赛辽宁省预赛试题)已知x+y=1,问：当实数x、y为何值时，(x3+1)(y3+1)取得最大值？

评注：本题的难点在于如何将已知条件进行转化，再构造新函数.这要求我们在解题中需要有一双“慧眼”，观察发现问题的本质，从而找到解题的切入点.

8.变更主元法

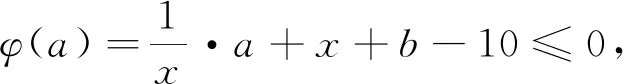
9.数形结合法

例10 (2012年全国高中数学联赛浙江省预赛试题)已知实数a、b、c、d满足ab=c2+d2=1,则(a-c)2+(b-d)2的最小值为.

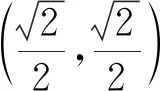
评注：本题条件与所求结果均具有几何意义，借助解析几何的思想方法，数形结合，将抽象变成了直观，可化难为易，化繁为简.

多变量最值问题的解决方法较为灵活多变，没有固定的模式，但总的指导思想就是减元，尽量化为一元问题来处理，转化的过程主要是根据题中条件与结论的特征来寻找突破口.所以我们在解题过程中要注重知识间的内在联系，抓住问题的本质.有时也可转换视角来观察条件和结论.多元变量求最值问题不仅可以提升学生的思维能力，更能提高学生的数学核心素养.