基于卡尔曼滤波算法的MMC子模块IGBT在线监测方法
周 刚
(国网福建省电力有限公司,福建 福州 350012)
0 引言
模块化多电平换流器(module multilevel converter,MMC)自提出以来,在直流输电中得到了广泛应用[1].MMC不仅有传统变换器的输出特性和结构优势,还具有抑制谐波[2-3]和故障保护[4-5]等优点.子模块中绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)的开关管和二极管在运行过程中会逐渐老化,进而对系统安全运行造成威胁[6].因此,研究在线监测MMC子模块IGBT状态参数具有重要的工程意义.目前,MMC子模块IGBT状态监测已得到相关学者的关注.Astigarraga 等[7]提出基于IGBT的壳体温度、导通压降和通态电流3个变量进行寿命预测和老化测试,随着导通压降的增大,元件寿命逐渐减少;Xiong 等[8]通过功率循环加速测试,利用IGBT导通压降的变化估计IGBT的性能.但上述方法对IGBT状态参数的提取需要在测量电路中增加采集量,使得系统更加复杂,还降低了输电系统的可靠性.
以上方法仅关注IGBT状态参数检测方法的研究,并没有对包括二极管在内的IGBT模块进行监测.本研究针对以上不足,提出基于卡尔曼滤波算法对MMC子模块IGBT中的开关管和二极管的状态参数同时在线实时监测的方法.在保证精度估计MMC中IGBT和二极管的同时,基于已配置的子模块电容电压传感器测量数据,采用卡尔曼滤波算法对MMC子模块IGBT中的开关管和二极管的通态电压偏置和通态电阻进行估计,降低电压电流测量误差及离散过程中量化误差等因素对状态参数估计的不良影响.
1 MMC结构和工作原理
1.1 MMC拓扑结构

图1 MMC拓扑结构图Fig.1 MMC topology diagram
MMC的拓扑结构如图1所示.模块化多电平换流器由三相组成,每相有上下两个由n个子模块(SM)级联而成的桥臂.各个子模块中,T1、T2为IGBT开关元件,D1、D2为与IGBT反并联的二极管.Udc和Idc分别为直流侧的电压和电流,O为零电位参考点.
1.2 MMC工作原理
MMC处于运行状态时,它的子模块工作模式有: 当T1门极加开通信号、T2加关断信号时,子模块电容器接入电路投入运行,在不同的直流侧电流方向下电容器分别处于充电或放电状态;当T1加关断信号、T2加开通信号时,子模块电容器被旁路,此时电容器电压为0,子模块端电压为T2或D2的导通压降.
子模块中,IGBT和二极管的导通压降可近似线性表示[13]如下
UT=UT0+iT·rT
(1)
UD=UD0+iD·rD
(2)
其中:UT、UD分别为 IGBT开关管和二极管导通时的端电压,以开关器件导通方向为电压参考方向;iT为IGBT集电极电流;iD为二极管电流;UT0、UD0为通态电压偏置;rT、rD为通态电阻.
为了分析子模块工作状态,以MMC上桥臂为例,引入Sx、Sx1、Sx2、Sx3和Sx4表示第x个子模块的工作状态.Sx表示给T1的开关信号,开通信号为1,关断信号为0;Sx1、Sx2、Sx3和Sx4分别表示子模块中T1、T2、D1、D2的导通状态,导通为1,截止为0.子模块的工作状态和对应的端电压Usmx由Sx和桥臂电流ipj的方向决定,具体如表1所示.T1门极加开通信号Sx=1时,当桥臂电流ipj<0,子模块电容器处于投入状态且T1导通,子模块端电压为UCx-UT1x,当桥臂电流ipj>0,子模块电容器处于投入状态且D1导通,子模块端电压为UCx+UD1x;T1门极加关断信号Sx=0时,当桥臂电流ipj>0,子模块电容器处于旁路状态且T2导通,子模块端电压为UT2x,当桥臂电流ipj<0,子模块电容器处于旁路状态且D2导通,子模块端电压为UD2x.

表1 不同工作状态子模块端电压
2 卡尔曼滤波算法
卡尔曼滤波算法是一种递推最优且线性最小均方的估计滤波算法,因其良好的性能在许多场合得到了广泛应用,算法采用递推,从量测信息中提取被估计量信息并积存在估计值中,且广泛应用于在线估计电力系统的状态参数[9-12],与其他递归算法相比,其主要优点能够消除可能由传感器引起的测量噪声的影响,并且有较强的适应性[13-14].针对IGBT参数在线估计而言,其噪声特性难以获取,应用该算法最为合适.对于一个系统,首先应能用以下线性微分方程进行描述
Xk=AXk-1+qk-1
(3)
Zk=HXk+rk
(4)
其中:Xk、Zk、qk、rk分别为k时刻系统的状态量、量测量以及过程噪声和测量噪声;A为k-1时刻到k时刻的一步转移阵,在本应用中,A为单位矩阵;H为量测阵,两者均由系统本身决定.式(3)为系统的量测方程.
卡尔曼滤波算法的步骤如表2所示.X为一列向量,其元素即系统的各个状态量;P为系统估计误差协方差矩阵;Q为系统噪声序列的方差阵;r为量测噪声方差.

表2 卡尔曼滤波算法
3 子模块状态参数估计方法
本研究所述MMC状态参数估计方法监测子模块IGBT的开关管和二极管的通态电压偏置及通态电阻,需要在MMC的每个桥臂上配置n+2个传感器监测必要的电气量.其中电压传感器有n+1个,即n个子模块电容器上各加一电压传感器测电容电压UCx,以及桥臂上一个电压传感器测桥臂电压US;电流传感器仅需一个,测桥臂电流ipj.在MMC实际运行时,这些传感器往往是已配置的,并不需要额外增设.通过以上电气量可以计算估计MMC状态参数,实现在线监测.
MMC由子模块导通情况以及KVL可知三相完全对称,上下桥臂的工作情况也是完全相同的,故以A相的上桥臂为例进行说明和验证.结合表1子模块导通情况,桥臂上第x个子模块的端电压可如下式表示
Usmx=SxUCx-Sx1UT1x+Sx2UT2x+Sx3UD1x-Sx4UD2x
(5)
而一个桥臂由n个子模块级联而成,故桥臂电压可以由桥臂上所有子模块端电压求和得到
其中Us(ti)为ti时刻的桥臂电压.将式(6)移项得
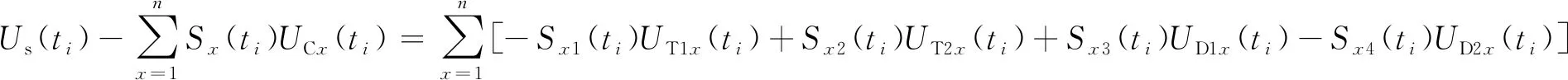
(7)
由式(1)、(2)可知,第x个子模块上IGBT和二极管的导通压降为
UT1x(ti)=UT1x0(ti)-ipj(ti)·rT1x(ti)
(8)
UT2x(ti)=UT2x0(ti)+ipj(ti)·rT2x(ti)
(9)
UD1x(ti)=UD1x0(ti)+ipj(ti)·rD1x(ti)
(10)
UD2x(ti)=UD2x0(ti)-ipj(ti)·rD2x(ti)
(11)
式(8)~(11)中,UT1x0(ti)、UT2x0(ti)、UD1x0(ti)、UD2x0(ti)表示该子模块对应元件的通态电压偏置,rT1x(ti)、rT2x(ti)、rD1x(ti)、rD2x(ti)则表示通态电阻.将式(8)~(11)代入式(7)并写成矩阵形式

(12)
式(12)中,UT1s0(ti)、UT2s0(ti)、UD1s0(ti)、UD2s0(ti)分别表示ti时刻桥臂上所有子模块IGBT的两个开关管即T1、T2和二极管D1、D2的通态电压偏置,rT1s(ti)、rT2s(ti)、rD1s(ti)、rD2s(ti)表示ti时刻桥臂上所有子模块两个IGBT即T1、T2和二极管D1、D2的通态电阻,均为n维列向量;Ss1、Ss2、Ss3、Ss4为对应元件的实际导通状态,为n维行向量.
为表述简洁,令
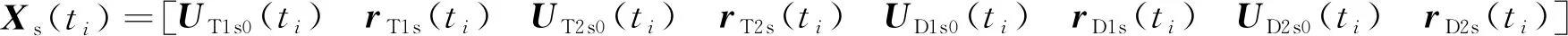
(13)

(14)
其中:Xs(ti)表示一个桥臂上所有子模块的IGBT和二极管的状态参数.又因为流过各个子模块的IGBT和二极管的电流可以表示为
iT1s(ti)=Ssl(ti)·ipj(ti)
(15)
iT2s(ti)=Ss2(ti)·ipj(ti)
(16)
iD1s(ti)=Ss3(ti)·ipj(ti)
(17)
iD2s(ti)=Ss4(ti)·ipj(ti)
(18)
所以式(14)可表示为
Φs(ti)=[-Ss1(ti)iT1s(ti)Ss2(ti)iT2s(ti)Ss3(ti)iD1s(ti) -Ss4(ti)iD2s(ti)]
(19)
因此,桥臂电压与桥臂上所有子模块的IGBT的开关管和二极管的状态参数的关系式为
Us(ti)-Ss(ti)UC(ti)=Φs(ti)Xs(ti)
(20)
式(20)中,Φs(ti)为8n维行向量,Xs(ti)为8n维列向量.
结合上节所述卡尔曼滤波算法,首先设定状态量和协方差矩阵的初值Xs(t0)和P(t0).状态量的初值一般定得较小,本研究将Xs(t0)设为零向量;再设协方差矩阵的初值P(t0)=MI,其中,M为任取的大于0的常数,I为8n阶的单位矩阵.Q是过程噪声.因此tk时刻,卡尔曼增益为
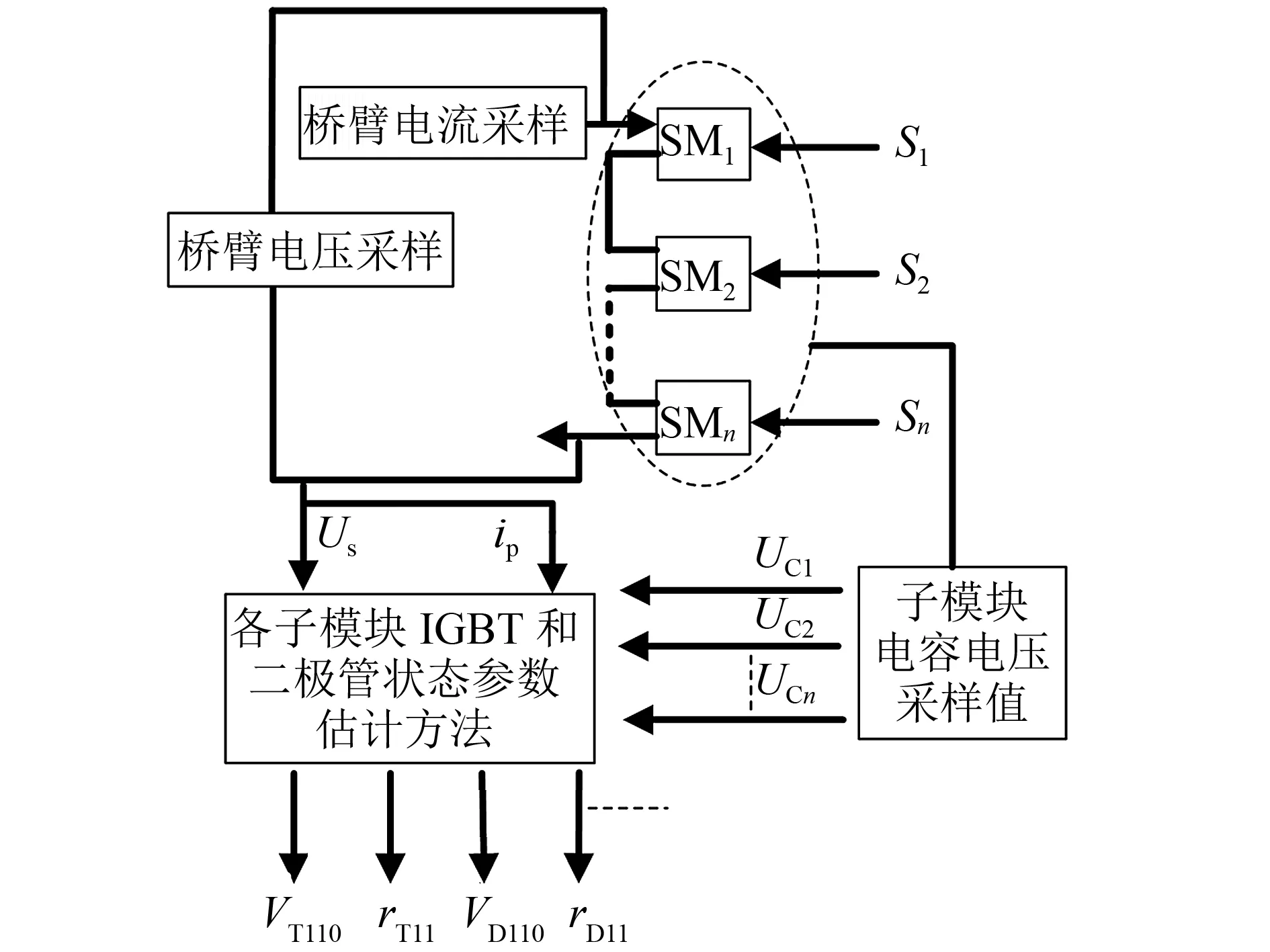
图2 传感器配置及状态参数估计方法Fig.2 Sensors configuration and state parameter estimation method
其中:K(tk)分别是8n维列向量;R(tk)是量测噪声.
tk时刻更新系统状态估计值和误差协方差矩阵为
Xs(tk)=Xs(tk-1)+K(tk)(Us(tk)-Ss(tk)UC(tk)-
Φs(tk-1)Xs(tk-1))
(22)
P1(tk)=P1(tk-1)-

(23)
于是可以得到tk时刻同一桥臂上所有子模块IGBT的开关管和二极管的状态参数估计结果,按以上步骤不断重新迭代,直至收敛,即可不断更新状态参数,实现在线估计.传感器配置及状态参数估计方法如图2所示.
4 仿真分析
为验证本研究所提的同时监测MMC桥臂上各子模块IGBT的开关管和二极管状态参数的方法,在PSCAD/EMTDC搭建MMC-HVDC系统进行仿真验证.在任何一个实际系统中,都存在量测噪声,在卡尔曼滤波算法中,一般认为这种噪声为高斯白噪声,因此传感器的测量噪声可以认为是服从均值为0,方差为Qk的正态分布的噪声[15],可在测量系统中加入高斯白噪声模拟测量噪声.MMC-HVDC仿真系统的相关参数列于表3.

表3 MMC-HVDC系统参数
MMC中,各子模块开关器件的参数设置[9]如表4所示,结温25 ℃下,所有电容的电容值均取值2 800 μF.应用上文所述的监测估计状态参数方法,对IGBT的开关管、二极管的通态电压偏置和通态电阻同时进行估计,桥臂第1个子模块T1和D1估计结果如图3所示,其余子模块与第1个子模块的估计结果基本一致.其估计效果较好,能在0.1 s内收敛,收敛值与设定值几乎完全重合,误差在0.1%以下.由此可见,本研究所述基于卡尔曼滤波算法估计MMC子模块状态参数的方法是有效的,能得到足够准确的估计结果.

表4 不同结温下开关器件参数取值

图3 T1、D1状态参数估计结果(25 ℃)Fig.3 Estimation results of state parameters of T1,D1(25 ℃)
进一步研究算法参数适应性,MMC各开关器件可取结温125 ℃时的参数取值[9],为体现算法的适应性,在仿真中将子模块电容设置在较恶劣的情况,各桥臂6个子模块电容设置为不同的电容值,从3 000 μF起依次递增5%.仍采用图2所示的卡尔曼滤波算法,同时估计各子模块IGBT和二极管的状态参数,桥臂第1个子模块T1和D1估计结果如图4所示.在0.2 s后,状态参数估计结果均收敛于设定值,误差能达到0.1%以下.由此可知,在桥臂子模块中元件参数发生变化时,本研究提出的状态参数估计方法依然可行,算法参数有一定的适应性.

图4 T1、D1状态参数估计结果(125 ℃)Fig.4 Estimation results of state parameters of T1,D1(125 ℃)
5 结语
本研究提出一种基于卡尔曼滤波算法实时估计MMC子模块器件状态参数的方法,通过基于卡尔曼滤波算法的状态参数估计方法,能够快速收敛得到MMC各子模块IGBT中开关管和二极管的状态参数,估计误差在0.1%以下,得到的开关器件通态电压偏置和通态电阻可以用来预测MMC各子模块IGBT器件的运行状态,实现实时状态监测,以便在子模块IGBT出现老化时,操作人员及时更换.此外,该方法大大地减少了配置传感器的数目,节约了经济成本并提高了系统的可靠性.

