有向拓扑下网络化运动控制系统的容侵同步控制
(浙江工业大学 信息工程学院,杭州 310023)
0 引言
运动控制是现代机电领域的重要支柱,其不仅要求实现对单轴系统的速度、位置等物理量的控制,更要提高具有运动协调关系的多轴系统间的同步控制精度。对于纺织印刷机械、数控机床、机器人等复杂设备,多轴之间的同步运动是保证控制性能、提高产品质量的关键。
另一方面,随着网络通信技术的普及,网络化给现代运动控制注入了活力。运动控制网络化的应用,为多轴控制带来了巨大便利,同时也为多轴系统的同步控制精度带来了更大的挑战。
网络化运动控制系统是网络通信技术与运动控制系统的有机结合体,它具有控制精度高、开放程度高等特点。但是,由于网络化运动控制系统易受到网络空间的攻击,其同步控制过程中的稳定性常常不能得到保证。
近年来,学界在网络化容侵同步控制方面已经取得了一系列成果。Shao等[1]提出了一种互联非线性系统的分散容错控制方法,并利用小增益循环的方法来应对耦合效应,该方法可以在保持子系统之间原有状态的前提下实现容错控制。Zhong等[2]提出了一种基于故障估计器的时延反馈控制器,通过构造容错主从同步系统,获得了确保同步误差系统稳定性的充分条件。Qin等[3]提出了一种分布式传感器故障检测与隔离方案,将新的分布式控制法运用于车辆闭环模型中,实时证明了控制律和故障检测方案的有效性。Cao等[4]讨论了带有未知外部干扰的线性多智能体系统跟踪控制问题,提出一种基于分布式扩维状态观测器的跟踪控制策略。Wang等[5]研究了高阶多智能体系统的分布式容错控制问题,提出了一种基于分布式自适应机制的新型容错跟踪控制协议。Zuo等[13]研究了一类利普希茨非线性多智能体系统在执行器故障和领导者未知输入有界情况下的故障跟踪控制问题,提出了一种自适应容错控制协议,通过在线估计执行器故障来更新参数并实现跟踪控制。Chen等[14]研究了分布式自适应协议在多智能体系统中的容错一致性问题, 提出了一种分布式协议增益更新机制,实现了无领导者多智能体系统的分布式连续自适应容错一致性协议设计。在此基础上,提出了一种适用于多智能体系统的分布式容错领导-跟随者一致性协议。Zhang等[15]在有向通信拓扑结构下,利用线性矩阵不等式(LMI)研究了一种基于自适应观测器的分布式故障估计观测器,根据每个智能体的相对输出估计误差,构造各自的故障估计观测器。Ren等[16]研究二阶非线性随机多智能体系统的领导跟随一致性问题,其中每个跟随者的速度是不可测量的,因而为每个跟踪器建立分布式的“降阶观测器”来估计其未知速度,进而提出了一种基于无向连接拓扑结构的分布式控制器,证明了在逆步控制方法下,随机多智能体系统的一致误差可以收敛到原点附近的一个小区域。Li等[17]研究了一类具有外部干扰和执行器/传感器故障的交换网络化控制系统(SNCSs)问题。同时,在通信网络中考虑了网络诱导时延、丢包和包无序等通信约束,提出了一种基于观测器和二阶离散自适应滑模函数的鲁棒自适应滑模控制方法,进而证明了滑模面的可达性。
多智能体容错控制方面的结果多集中于状态反馈控制策略,近年来也出现了少量多智能体输出反馈容错控制问题的研究结果。如文献[11]考虑了无向通信拓扑下的多智能体系统容错控制问题,而文献[12]则考虑了有向通信拓扑下的多智能体系统鲁棒跟踪控制问题。需要指出,实际系统中往往非线性未建模不确定性,已有文献如[13]通常假设非线性不确定性结构已知且满足利普希茨条件,这样处理往往会使得系统稳定性条件具有很大的保守性。
根据上述分析,本文针对带有一般有向通信拓扑的不确定网络化多轴运动控制系统的容侵同步控制问题展开研究,提出了一种有向拓扑下基于分布式中间观测器的容侵同步控制方法。将未知非线性不确定性分解为匹配和不匹配分量,对匹配分量进行补偿控制,同时通过调节特定参数对不匹配分量进行有效抑制。
1 网络化多轴运动控制系统
1.1 网络化多轴运动控制系统组成和工作原理
本文所考虑的网络化多轴运动控制系统实物图与结构图如图1所示,左侧为多轴同步系统,右侧为双轴雕刻机系统。其主要由PC(上位机)、ARM单片机(下位机)、电机、交流伺服系统和CAN总线组成。

图1 多轴运动控制系统
其中,下位机采用基于ARM的CortexTM-M4为内核的STM32F407系列高性能微处理器。该处理器运算速度快、精度高,且其内部集成了大量可供立即使用的接口资源,满足了网络化运动控制系统对处理器的要求。
选用台达ASDA-A2-M型驱动器作为交流伺服系统的驱动部件,其内置运动控制模式,含电子凸轮功能,支持多种轴孔操作需求,并且可在低速运转下实现精准定位控制。
本系统选用CAN 总线实现下位机与伺服系统之间的网络化通讯控制。CAN总线是一种基于国际标准的能够实现分布式控制或实时控制的串行通信网络,具有较高的通信速率和较强的抗干扰能力。基于CAN总线的分布式控制系统具有明显的优越性,因为CAN总线具有避免总线冲突的特点,在非破坏性的前提下提高了实时性。
该网络化多轴运动控制系统的主要控制过程如下:上位机通过TCP/IP协议接收来自下位机的数据信息并根据控制算法更新控制律,并将新的控制指令下发至下位机。下位机作为中转站,接收上位机的控制指令,将TCP/IP协议数据包重新封装为CAN总线数据包,并通过CAN总线将其传输至各交流伺服系统。同时,下位机通过CAN总线实时获取各交流伺服系统的位置、速度、力矩等信息,并将这些数据封装成TCP/IP协议数据包后发送至上位机。CAN总线负责进行下位机与交流伺服系统之间的通讯,并实时传输数据。交流伺服系统实时响应来自上位机的控制指令,并由电机或电机驱动的机械臂做出相应的运动响应。
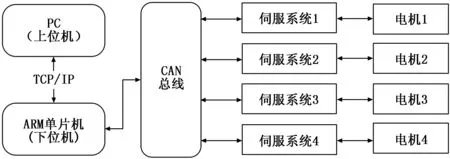
图2 系统结构
针对上述多轴运动控制系统。考虑其存在如图3所示的有向通信拓扑图。其中,电机间的单向箭头表示该节点的测量输出信息可以发送给另一个对象,但不接受信息的反向传递。
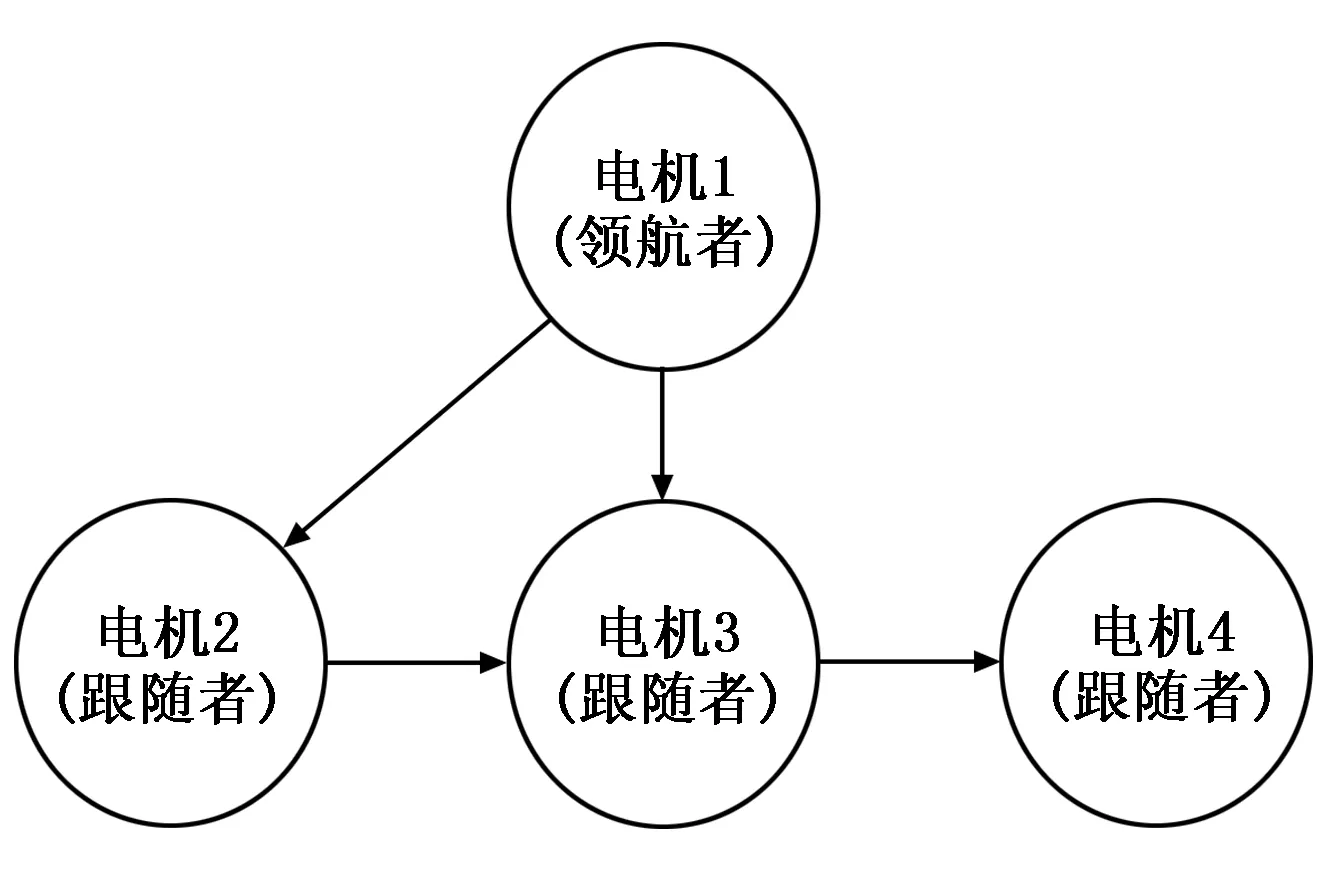
图3 通信拓扑
对一个实际的网络化多轴运动控制系统来说,相比无向通信结构,其拓扑结构为有向通信结构时更具适用性。因为有向通信只需满足单向通信,而无向通信需满足双向的通信条件,因此有向通信是更为普遍适用的情况。运用有向通信拓扑结构可以大大简化系统复杂度、降低对网络计算能力的要求,从而节约系统成本。
定义邻接矩阵A=[aij]∈RN×N,其中aii=0;当(i,j)∈ε时,aij=1;否则aij=0。牵引矩阵D=diag{di}∈RN×N和Laplacian矩阵L=[lij]∈RN×N来表示电机间的信息传递关系。在有向通信拓扑情况下,S和L均为非对称矩阵。上述矩阵定义如下:
(1)
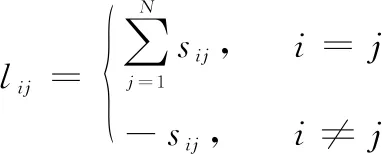
(2)
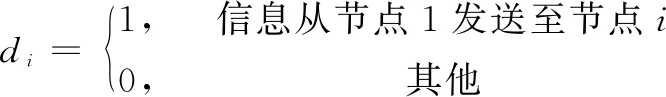
(3)
由于电机间存在一定的网络通信拓扑,当多轴运动控制系统中的任意一轴受到外部攻击时,攻击效应会随着拓扑结构扩散到整个系统,从而影响系统性能。因此,本文针对有向通信拓扑下的不确定网络化多轴运动控制系统,提出了一种基于中间观测器的容侵同步控制方法,确保系统具有良好的容侵同步性能。
1.2 网络化多轴运动控制系统模型
根据伺服系统特性,在速度模式下,对系统模型进行辨识,得到伺服系统的传递函数如下所示:
(4)
其中:ai、bi为模型的定常参量,Ui(s)为多轴伺服系统轴i的速度设定值,Yi(s)为多轴伺服系统轴i的位置设定值。xpi(t)和xvi(t)分别为系统轴i的位置量和速度量,ui(t)为系统轴i的控制输入,yi(t)为系统轴i的测量输出。
根据上文分析,在该控制系统中共有一个领航者(电机1)和三个跟随者(电机2、3和4)。将式(4)转化为状态空间方程,并考虑系统建模非线性误差,得到领航者的系统模型为:
(5)
y0(t)=Cx0(t)
(6)
其中:x0(t)∈Rn是领航者的状态,y0(t)∈Rm是领航者的测量输出,r0(t)是领航者的输入,G(t,x0(t))∈Rn是未知非线性函数,表示系统未建模不确定性。A、B和C为适当维度的常数矩阵。
考虑如下带有建模非线性误差和执行器攻击的跟随者系统模型:
(7)
yi(t)=Cxi(t)
(8)
i=1,2,…,N,其中xi(t)∈Rn、ui(t)∈Rm、fi(t)∈Rm、yi(t)∈Rp、G(t,xi(t))分别为第i个追随者的状态、控制输入、执行器攻击、测量输出和非线性部分,且满足m≤p≤n。
定义第i个跟随者的跟踪误差δi(t)=xi(t)-x0(t)。由式(5)~(8)可以得到第i个跟随者的跟踪误差系统:
(9)
其中:ηi(t)=fi(t)-r0(t),Ge(t)=G(t,x(t))-G(t,x0(t))。
将Ge(t)分解为Ge1(t)和Ge2(t)。其中,Ge1(t)为匹配非线性部分,Ge2(t)为不匹配非线性部分。则式(9)可以重写为:
(10)
将执行器攻击、领航者的参考输入和非线性部分重新合并成一个组合未知信号:
ηi(t)=fi(t)-r0(t)+B*Ge1(t)
本文的控制目标是针对有向拓扑下网络化多轴运动控制系统,设计容侵同步控制协议,确保跟踪误差系统的状态一致最终有界。
2 2容侵同步控制设计
2.1 2.1分布式中间观测器和控制协议
先定义中间变量为:
ξi(t)=ηi(t)-ωBTδi(t)
(11)
其中:ω>0是一个可调参数。需要指出,ω是分布式中间观测器的关键参数,实际上,ω和观测器的收敛速度相关,同时通过调节ω可以改善分布式观测器的跟踪估计性能。
根据式(10)~(11),设计第i个跟随者的分布式中间观测器为:
(12)
(13)
(14)
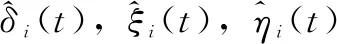
根据上文的分析,设计第i个跟随者的容侵同步控制协议为:
(15)
其中:K为控制器增益,其取值可通过令A-BK为Hurwitz矩阵获得。
在一般有向通讯拓扑条件下,每个跟随者电机会依据通信拓扑结构与相邻电机交换测量输出信息,并通过生成树的信息传递机制确保能够对与领航者电机的跟踪误差进行实时在线估计并实现同步控制。
2.2 跟踪误差系统稳定性分析
将上文设计的协议代入跟踪误差系统,得到如下全局跟踪误差系统其中,其中M=L+D:
(IN⊗B)eξ(t)+(IN⊗ωBBT)eδ(t)+
(IN⊗Ge2(t))
(16)
(IN⊗ωBBT)eδ(t)-(cM⊗FC)eδ(t)+
(IN⊗Ge2(t))
(17)
(IN⊗+Ge2(t))
(18)
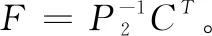
定理1:如果给定标量ω>0,ε>0,若存在矩阵Pj>0,j=1,2,3以及参数c>0,使得:
(19)
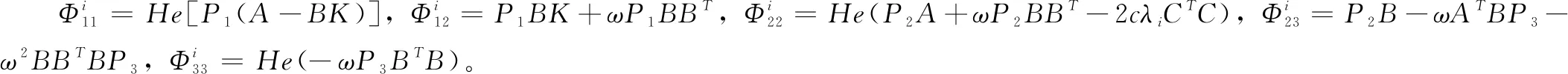
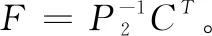
证明:选择Lyapunov函数为:
(20)
对上式求导,结合(16)-(18)可以得到V(t)关于时间的导数。为简便起见,后续推导省略,详细过程可参考文献[8]。证毕。
由于实际系统中往往非线性未建模不确定性,而已有文献如[7]通常假设非线性不确定性结构已知且满足利普希茨条件,这样处理往往会使得系统稳定性条件具有很大的保守性。本文方法将未知非线性不确定性进行分解,对匹配分量进行补偿控制,同时通过调节特定参数对不匹配分量进行有效抑制,从而减少了不等式放缩给闭环系统稳定性带来的保守性。
2.3 2.3容侵同步控制具体步骤
基于分布式中间观测器的容侵同步控制过程主要由以下几个步骤组成:
1)获取领航者电机和各跟随者电机在运行时的数据;
2)设定调节参数ω及系统反馈增益矩阵K;
3)分别计算观测器增益c和F;
4)运用分布式中间观测器对跟踪误差系统的状态和组合未知信号进行估计。若输出估计误差超过设定的阈值,则需重新调节系统的参数并计算相应的观测器增益c和F,直至输出估计误差小于阈值为止;
5)利用估计值设计反馈控制律,对信号进行实时补偿,完成对多轴运动系统的容侵同步控制;
6)获取下一时刻的数据,重复上述2)~5)步骤。
上述具体流程如图(4)所示。

图4 容侵同步控制流程图
3 实验结果与分析
为说明前述容侵同步控制方法的有效性,本节给出了在网络化多轴运动控制系统上的实验结果。
网络化多轴运动控制系统的上位机界面是使用Microsoft Visual Studio 2015编写的。Microsoft Visual Studio是美国微软公司的开发工具包系列产品,是一个基本完整的开发工具集,它包括了整个软件生命周期中所需要的大部分工具,如UML工具、代码管控工具、集成开发环境(IDE)等等,能够帮助开发人员打造跨平台的应用程序及创建跨平台运行的ASP.NET 5网站,从Windows到Linux、甚至iOS和Android都可以轻松搞定。上位机操作界面主要由C++语言进行编写,并结合MFC制作人机交互界面。连接服务器(ARM单片机)时需要将本机IP设置为和服务器IP同簇。同时由于系统传递函数是在速度模式下辨识得到的,因此需要将算法写入速度模式,并将组合未知信号及其估计和系统状态等所需要的曲线实时显示在上位机平台的画图区域内。

图5 网络化多轴运动控制系统上位机界面
各个电机系统参数为:
并设置执行器攻击分别为:
f1(t)=sin(0.5t),f2(t)=0.8sin(0.6t),
f3(t)=1.5sin(0.4t)
领航者的输入r0(t)对于所有跟随者是非可见的。假设其为:r0(t)=0.5sin(0.2t)。根据领航者和跟随者的有向图通信拓扑结构图3以及容侵同步控制协议式(15),设定系统反馈增益矩阵K=[14.6698 23.5635],调节参数ω=4。根据式(19)计算得到观测器增益:c=2385.9,F=[0.0469 0.6023]T。
利用观测器对系统状态和未知信号进行估计,发现误差超出了设定阈值(±0.5),不满足设定的性能指标,因此对参数进行调节使ω=4.5,并重新根据式(19)计算观测器增益:c=9871.6,F=[0.0325 0.8044]T。
图6~8分别给出了组合未知信号ηi(t)的估计值及其误差,并且各自的估计误差均在允许范围内(±0.5)。然而由于不确定实际值无法获得,因此我们仅能提供由领航者非零输入和执行器攻击所构成的组合信号与估计值作比较。其中,黑线代表组合未知信号的实际值,蓝线表示组合未知信号的估计值。图9给出了领航者和跟随者的状态1(位置)和状态2(速度)的跟踪曲线,可以看出,其稳态跟踪误差也均在允许范围内。
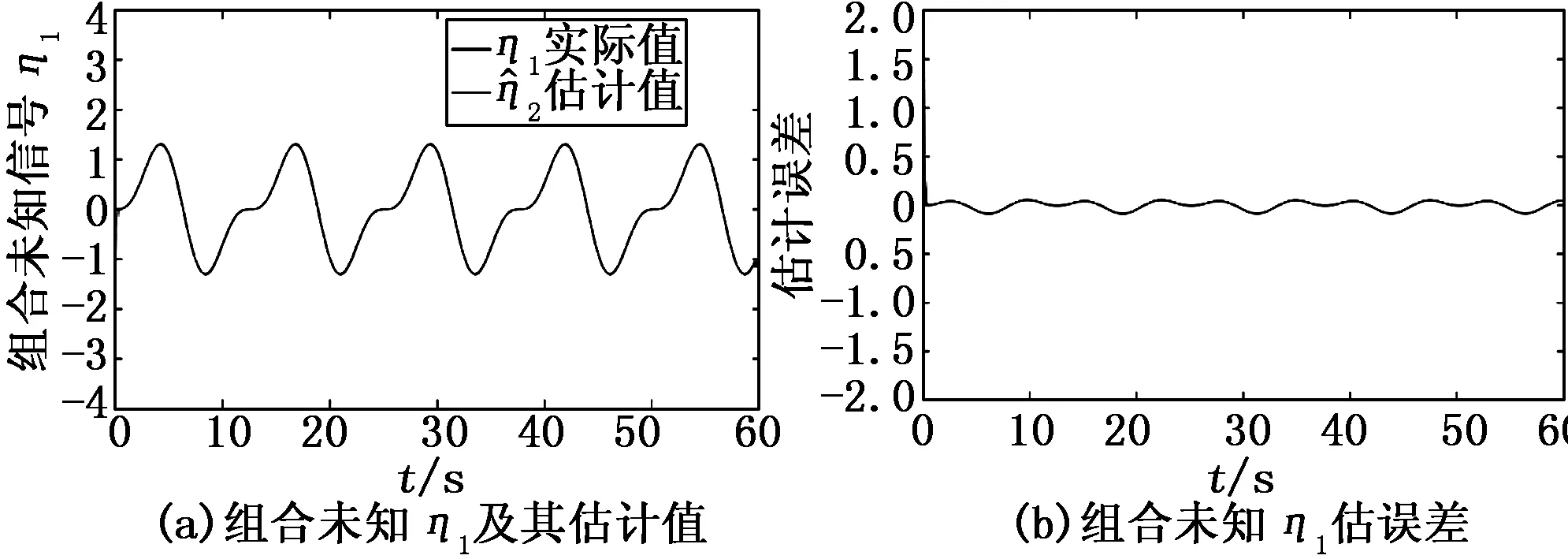
图6 η1估计以及误差
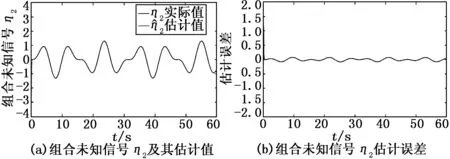
图7 η2估计以及误差
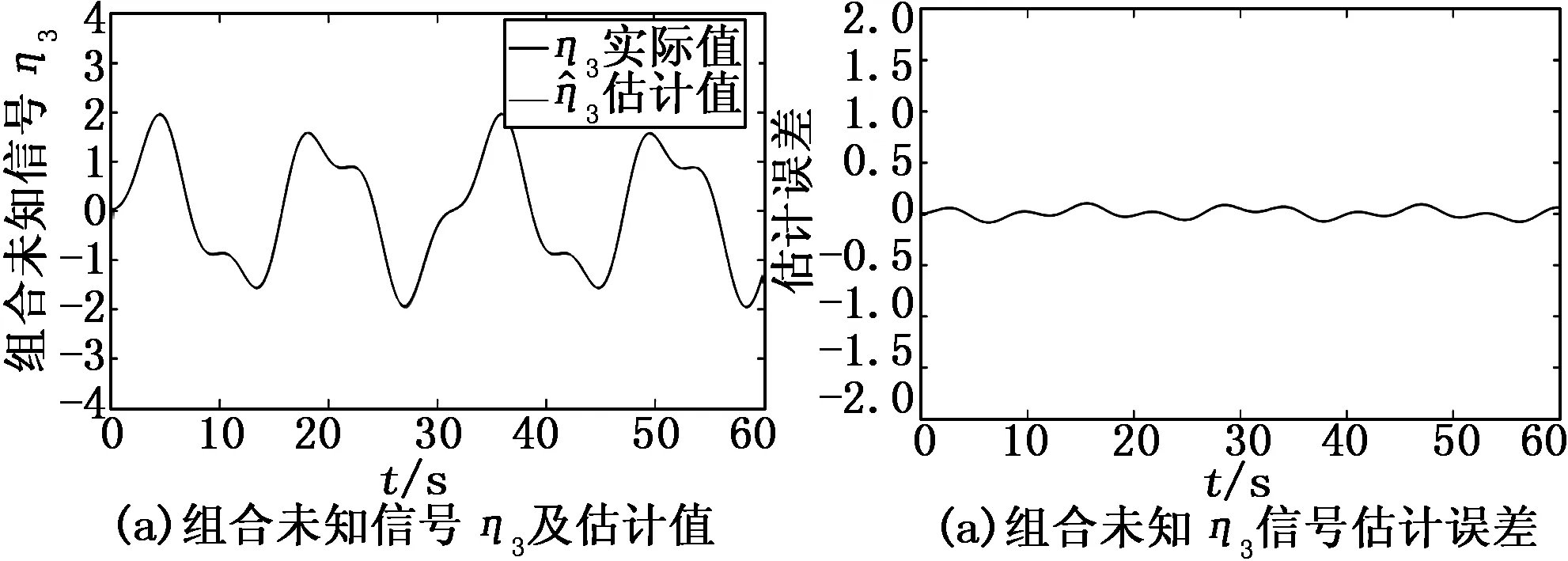
图8 η3估计以及误差
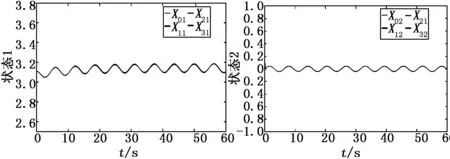
图9 状态1、2跟踪曲线
根据实验结果可知,本文提出的容侵同步控制方法不仅准确估计了系统的位置(状态1)、速度(状态2)以及组合未知信号(包含攻击信号、领航者输入以及未建模不确定性),而且,依据上述估计值所设计的具有攻击补偿的反馈控制律能够确保跟随者与领航者之间的状态同步,因此该方法具有良好的容侵同步控制性能。
4 结束语
针对执行器攻击下有向通信拓扑的网络化运动控制系统,提出了一种基于分布式中间观测器的容侵同步控制方法,通过设计分布式中间观测器估计系统所受到的攻击,并且利用系统状态值和攻击估计值设计容侵同步控制协议,实验结果说明在执行器攻击威胁和不确定性因素影响下,所提方法网络化运动控制系统仍具有较好的同步控制精度和鲁棒性,因而该方法在工程上具有一定的应用价值。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

