有限元法在岩质边坡稳定性分析中的应用示例

常思源　陈柘舟　柴利杰　刘建凯　赵晨曦　杨艳峰　刘明坤

摘 要：本文讨论了岩质边坡失稳破坏的成灾机理及影响因素，对边坡稳定性分析的常规方法进行了分析比较，提出边坡内部应力水平和分布是影响边坡稳定性的决定性因素。以北京门头沟山区某一滑移式崩塌隐患点为研究对象，采用有限元数值模拟方法分析比较软弱夹层对边坡体内应力、应变场的影响，说明了岩质边坡由软弱夹层及其强度指标所决定的重力破坏机理，并对有限元数值方法存在的不足和问题提出思考。

关键词：岩质边坡;破坏机理;稳定性分析;软弱结构面;数值模拟;有限元法

Abstract： This paper introduces the mechanism and influencing factors of rock slope instability and failure， analyzes and compares the conventional methods for slope stability analysis. It is proposed that the internal stress level and distribution of the slope are the decisive factors affecting the stability of the slope. The influence of weak interlayer on the stress and strain field in a rock slope with potential collapse in the Mentougou area in Beijing are analyzed by finite element method. The analysis results reveal that the gravity failure of a rock slope is determined by weak structures and their strength. At last， the shortcomings and problems of the finite element numerical method are pondered.

Keywords： rock slope; failure mechanism; stability analysis; weak structural plane; numerical simulation; finite element method

0 引言

随着城市规模扩大以及城市路网向周边山区辐射延伸，人类工程活动需对山体开挖，形成人工岩（土）质边坡。以北京地区为例，北京地处太行山山脉和燕山山脉交汇处，地形和地质条件复杂，地质构造非常发育，岩层风化破碎严重，新构造运动频繁，加之人类活动剧烈，致使北京地区地质环境比较脆弱，地质灾害较为发育，且灾种多，群发性强（赵忠海，2009）。

据统计，截至2019年5月31日（黄来源，2020），北京市突发性地质灾害隐患点5037处，其中崩塌隐患2609处，占51.8%。2014—2016年間发生崩塌灾害共37次，岩质边坡崩塌32次，岩体一般顺坡坡度40°～65°，且多发于汛期。例如2016年7月房山河北镇108国道复线9 km+720～770 m发生的滑移式崩塌，造成道路堵塞及该段路面、护栏、水管等设施损毁。2016年8月，房山霞云岭乡庄户台村台儿港沟口西北侧发生滑移式崩塌灾害，掩埋房屋7间，损毁10间。据调查统计，自新中国成立以来，北京山区崩（滑）塌灾害直接造成35人死亡，700多间房屋被毁，大量农田、树木被毁，其相当比例的灾后堆积物更是直接成为泥石流发生所需的物质来源（贾三满等，2017）。

以崩塌发生模式来看，北京山区崩塌灾害以倾倒式和滑移式最为常见，分别占崩塌隐患总数的34.6 %和33.6 %（韩建超，2020）。其中滑移式崩塌是一种发生频率较高的山区突发性地质灾害。当边坡坡体有软弱结构面（体）存在时，当其倾向与坡向相同时，软弱结构面上覆的不稳定岩体在重力作用下具有向临空面滑移的趋势，不稳定岩体的重心滑出陡坡，就会产生突然的崩塌（潘懋等，2002）。该灾害多发育于坚硬、性脆、构造节理发育的砂岩、花岗岩、石英岩、碳酸盐岩中，具分布散、规模小，受水力作用影响较大且多发于汛期等特点。

为更好的对边坡隐患进行防治，应综合考虑岩质边坡的破坏类型、规模、影响范围等诸多因素，采取适宜的分析方法深入研究边坡的破坏形式和破坏机理，对边坡稳定性做出科学、客观、可靠的分析评价，选取有效的防止措施，避免造成人民生命财产安全的损失，提高工程的经济效益。

1 边坡地质灾害形成机理分类及边坡稳定性影响因素

1.1 边坡地质灾害形成机理分类

岩质边坡的破坏形式主要为滑坡和崩塌两种类型，成灾机理有相似的地方又存在很多不同，岩质边坡成为灾害隐患，具有许多复杂的成因，灾害成因受自身岩体结构及强度、自然外力和人类活动等多方面因素影响，但其实质是多方因素综合作用的结果，其破坏机理与边坡岩体的变形及应力分布、应变水平有紧密联系，根据的形成机理可按表1、表2进行分类。

滑坡：可根据滑坡体的物质组成、形成原因及滑动形式对滑坡进行分类，较典型的岩质边坡的滑坡分类见表1。

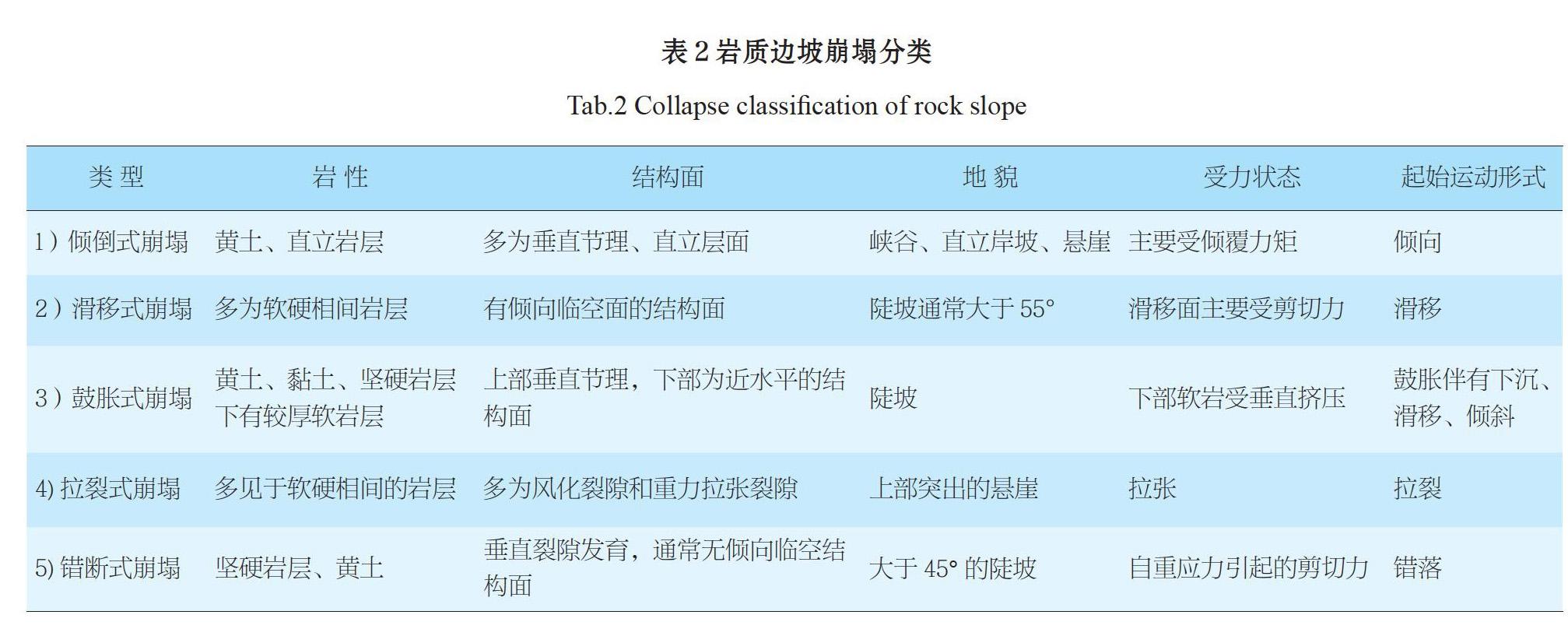
崩塌：崩塌多发生在陡峭边坡地段，一般坡度大于55°，高陡岩质边坡在在节理裂隙发育，岩体破碎，各种软弱结构面的组合位于不利情况下，极易发生崩塌。典型的岩质边坡崩塌分类可见表2。

1.2 边坡稳定性影响因素

（1）岩体结构

岩体结构是决定失稳形式的影响因素中最直接和重要的因素（陈祖煜，1998）。岩体结构可分为块状、层状、碎裂、松散4大类（谷德振，1979）。

松散结构：岩性同破碎结构基本一致，岩体多为泥土夹体积较小的破碎岩块构成，软弱结构面发育成网状。边坡稳定性差，边坡稳定性主要受岩体的抗剪强度控制。

破碎结构：岩性可为构造影响带、破碎带、蚀变带或风化破碎的各种岩石，岩体结构面发育，分布无规则，破碎的岩块间存在咬合力。边坡稳定性一般较差，稳定性受岩块间的摩擦力及咬合力控制。

层状结构：岩性一般为沉积岩、层状变质岩或多次喷发的岩浆岩，岩体多成互层状，结构面发育，软弱夹层或层间错动多为贯穿结构面。边坡稳定性受包括岩层走向、岩层与坡面夹角、岩层倾角组合、岩层厚度、层间结合能力、反倾结构面发育程度及强度等因素控制。

块状结构：岩性一般为岩浆岩、中深变质岩、厚层沉积岩，岩体成块状或厚层状，结构面不发育，多为刚性结构面。所形成的边坡稳定条件好，易形成高陡边坡，失稳破坏形式多为沿某一组结构面崩塌或滑动，边坡稳定性受结构面抗剪强度和岩石抗剪强度控制。

（2）水作用

多数失稳破坏都与水有关，水的作用主要为物理、化学作用及力学效应。

物理作用包括：润滑、软化、泥化、强化结合水等作用;化学作用包括离子交换、氧化还原、水解、溶蚀及渗透作用等;力学作用主要为静水、动水压力。三种作用相互耦合，改变岩土体结构，对岩体受力过程产生复杂影响。

（3）振动外力作用

振动外力包括地震引起的地震力及爆破、机器运转引起的振动力。地震、爆破、机械振动作用表现为累积效应及触发效应，累积作用引发岩体松动、软弱破碎面相对位移增大，孔隙水压力上升等。触发作用导致处于临界状态的边坡瞬间失稳。

（4）其他作用

人类活动作用：主要表现为人类的工程活动对边坡稳定的影响，从而改变边坡的几何形态（高度、坡度、形状）和受力状态（堆载、卸荷）。

风化作用：边坡岩体受到后期风化作用，造成岩体强度降低、裂隙增加，从而影响边坡的稳定性，岩体裂隙在进一步风化时，可致使岩土体脱落、崩塌、滑移等发生。

气候作用：主要表现为温差、降雨、降雪及冻融等作用，这些因素会加速边坡岩体风化，进而造成边坡失稳。

2 岩质边坡稳定性分析评价方法

当前边坡稳定性分析的主流方法可分为定性分析方法和定量分析方法两大类（张丽等，2007）。

（1）定性分析方法

定性分析方法中比较有代表性的是赤平投影法、边坡类比法、坡率法。

赤平投影法：赤平投影法是图解法中较为经典且广泛应用的方法，该方法以岩质边坡稳定性影响因素中的岩体结构面（特别是软弱结构面）作为分析对象，在边坡勘查、测绘等工作基础上，对岩体结构面和边坡临空面产状的空间几何关系进行定性分析，进一步考虑结构面的力学性质和发育程度，对边坡稳定性做出定性判断。

边坡类比法：该方法主要根据边坡高度H、坡面投影长度L来进行类比计算，取同种边坡调查统计获得已知2组以上数据，根据已知边坡的稳定性，按关系式H=aLb统计确定常数a、b，确定拟建边坡设计的允许坡度。

坡率法：该方法根据相应规范查表，确定边坡坡率允许值，将边坡坡率允许值与边坡实际坡率进行对比，从而确定边坡稳定性的分析评价方法。

赤平投影法作为一种应用较为广泛的定性分析法，根据岩体结构面、软弱结构面和临空面的空间几何关系来判断稳定或失衡趋势。通过对众多边坡灾害的成因分析，灾害的发生往往是由于软弱结构体（面）最先达到临界破坏强度，导致边坡整体失稳，进而破坏成灾。边坡类比法和坡率法是通过边坡的外部几何形状等参数与边坡稳定性的统计关系，与经验数据或规范约定条件进行比对，进而判定边坡稳定分析。

（2）定量分析方法

极限平衡法为目前应用最多的定量分析方法，将边坡按一定条件划分为规则块体，分析每一块体的受力平衡条件并建立平衡方程，以求解安全系数来判别边坡是否稳定，主要包括圆弧滑动法（主要用于土质边坡分析）、平面滑动法、折线滑动法等，用上述方法求解边坡稳定性系数（通常为抗滑力（力矩）与下滑力（力矩）的比值），當稳定性系数大于某一临界值（该系数确定需根据边坡类型、安全等级或工程经验确定，一般大于1.0）时，边坡为稳定状态，等于1时为临界平衡状态，小于1时为欠稳定或不稳定状态。

极限平衡法综合考虑边坡几何形态、岩体强度指标、软弱结构体（面）摩擦力等诸多影响因素对边坡稳定性进行分析。该方法积累了大量工程经验，并以工程实践完善了计算参数的选取和修正，被证实是可行、可靠的边坡稳定性分析工作方法。但是该方法忽略了边坡内部应力场分布、应力水平对边坡稳定性的影响，仅从下滑力（力矩）与抗滑力（力矩）的比值是否大于安全系数来判定边坡是否稳定，因此该方法仍具有一定的局限性。

（3）有限元法

近年来随着计算机技术的发展，边坡稳定性分析的数值分析方法也在不断进步。尤其是计算分析软件中对于岩土体本构关系描述的不断改进，使得边坡稳定有限元数值模拟分析方法的功能越来越强。

采用有限元数值模拟方法进行稳定性分析，特别是三维模拟，不仅可以模拟复杂地层的应变相容性、静力许可以及本构关系，而且在建模和分析过程中可以较为充分纳入坡体几何形状、岩层不均匀性的影响。应用有限元方法求解分析主要涉及位移场、应力场两个场变量，主要分析步骤为：（1）连续体的离散化;（2）模型位移函数的确定;（3）根据实际边坡建立有限元模型;（4）将离散化单元集合成系统方程组;（5）求出各节点位移;（6）求出各单元的应力应变。

通过上述过程，即可将边坡体的位移、应力分布以数值和等值线图的方式表达，以供技术工程人员对边坡进行分析。

3 有限元法边坡稳定性模拟应用实例

3.1 研究分析思路

定性、定量分析方法无法对边坡应力水平及分布进行解答，更无法了解软弱结构体（面）对边坡应力场的影响。而有限元法求解可以输出位移、内力（弯矩）、应力、应变计算结果，从而对边坡应力场进行分析和评价。

为说明软弱结构面（体）强度对边坡应力场及应力分布的影响，本节实例研究的思路为：1）建立两种类型的边坡分析模型（模型Ⅰ—无软弱夹层均质岩体;模型Ⅱ—含软弱夹层的非均质岩体）;2）在相同荷载（重力）、边界条件下，求解模型Ⅰ、模型Ⅱ的位移、应变、应力水平;3）通过对比分析说明软弱结构面（体）存在对边坡应力分布和应力水平的影响。

3.2 分析模型建立

以门头沟南雁路某处岩质边坡隐患点为研究对象，建立模型。根据现场实际勘查及《门头沟区南雁路边坡地质灾害隐患防治工程地质调查及稳定性分析告》，该边坡现状为岩质斜坡，现状边坡坡面（261°∠39°～58°），总长约33.6 m，最大坡高约为23.0 m，坡顶表层为植被覆盖。边坡岩性为闪长玢岩，临空面岩体完整性表现为较破碎—破碎，岩体内节理裂隙和劈理等各级结构面发育—较发育，裂隙宽度1.0～3.0 cm，最大裂隙宽度达6.0 cm左右，岩体呈强风化—中等风化状。边坡岩体结构以碎裂结构为主，局部表现为块体结构。边坡现状见图1。

经现场勘查，该边坡坡面岩体受卸荷节理切割及风化作用使结构面和岩体抗剪强度降低，岩体裂隙发育，软硬岩体相间，硬质岩体为强风化—中风化玢岩，软弱岩层为全风化—强风化玢岩，现状边坡坡面产状为261°∠39°～58°，软弱岩体为顺坡，主要产状为243°∠11°～17°，该边坡有发生滑移式崩塌的潜在危险，破坏机理为软硬交界面（潜在滑面）剪切破坏。

数值模型几何尺寸同实际一致，边坡宽度33.6 m，坡面水平投影长度23.1 m，坡高23.0 m，坡度1∶0.9～1∶1.2，倾角约39°～58°。模型几何尺寸、坡面角度、软弱结构层分布位置与实际测绘数据基本一致，由于边坡两侧缺少测绘数据且不影响边坡整体稳定性，为便于計算收敛，将边坡两侧概化为直斜面，将实际坡面、软弱结构层面拟合为曲面。同时忽略风化作用造成的岩体强度不均性及其他结构面对岩体分割影响，仅考虑主要软弱结构层（软弱夹层）存在对应力场变化影响。由于缺少现场试验，边坡数值分析模型计算参数主要依据工程地质手册（2007）及GB 50330-2013《建筑边坡工程技术规范》综合取值，计算参数见表3。

模型计算荷载仅考虑重力，边界约束条件将坡背、坡底按固定约束考虑限制位移及转动;坡侧按铰约束考虑，限制位移。实体模型见图2，单元划分采用高阶单元划分，数值模型见图3（单元体尺寸0.6～1.1 m3，共划分单元7637个，节点1637个）。

3.3 计算结果及分析

3.3.1位移变形结果

（1）模型Ⅰ位移变形结果

图4表明位移变形最大区域为坡脚红色区域，计算最大变形为：0.00698 m。位移等值线可见图4，实际位移量较小，为便于观察位移方向及位移量，将图4位移量按2.5倍进行趋势放大后见图5（仅视觉效果，无数值变化），位移矢量见图6。

图4至图6表明，无软弱结构体的均质岩体边坡的变形最大位置位于坡脚位置附近，变形方向近垂直于底面，具下位移的趋势，主要变形为压缩变形。次要变形为坡面位移，根据图6箭头所示方向，变形方向为顺坡向下，位移方向水平夹角约为50°～60°，较边坡倾角（39°～58°）倾斜8°～11°。当边坡岩体按均质考虑时，变形特征类似于具有较高抗剪强度（黏聚力、摩擦角）的均质土边坡。

（2）模型Ⅱ位移变形结果

位移等值线可见图7，位移量按2.5倍进行趋势放大后见图8，位移矢量见图9。根据图7至图9显示，位移变形最大区域为软弱夹层上缘部位，计算最大变形为：0.00628 m。

图7至图9表明，含软弱结构的边坡的最大变形位移位于软弱结构层上缘坡面处，最大位移方向与软弱结构层位置顺坡方向基本一致，滑移方向顺坡向外，滑移角度约为37°～43°，介于软弱结构层倾角与该处坡面倾角之间，边坡由软弱结构层分割成上下两部分，上部位移量较大，具明显向顺坡面滑移的趋势。

3.3.2剪切应变结果

（1）模型Ⅰ剪切应变结果

根据图10、图11，边坡的最大剪切应变出现于坡顶，最大剪切应变0.00157988（无量纲），该处为最大剪切应变位置与实际情况不符，经分析可知这是由于坡背为固定约束端边界条件设定所致。

坡脚位置的剪切应变次之，位置与位移变形最大位置接近，剪切应变为0.00128396（无量纲）。坡面位置剪切应变最小，剔除坡背为最大剪切应变出现的情况，该结果与实际情况较为相符。

（2）模型Ⅱ剪切应变结果

根据剪切等值线云图12、图13，由于软弱结构层（软弱夹层）强度低，最大剪切应变出现于软弱结构层底部临空部位，最大剪切应变为0.00203039（无量纲），该结果与实际情况比较接近。同时坡背的剪切应变也较大，这是由于坡背设定为固定端约束边界条件的原因，该结果与实际情况不符。

3.3.3 数值模拟结果对比分析

无软弱结构层（软弱夹层）时存在，边坡最大变形位移位于坡脚位置，位移方向几乎垂直底面，主要为压缩变形。边坡次要变形位于坡面下缘，位移方向几乎与坡面顺坡方向平行，位移量与边坡几何形状及岩体强度有关。

坡脚位置为剪切应变最大，该处受上部岩体的挤压、剪切作用可能发生剪切破坏。坡面位置剪切应变相对较小，易受下部岩体的张拉作用，可能发生拉应力破坏。

当软弱结构层（软弱夹层）存在时，边坡最大变形位置为软弱结构层上缘坡面处，由于软弱结构层强度较低，该位置受力后位移十分明显，位移量及位移方向与软弱结构层空间位置、几何尺寸、强度指标有直接关联。

根据剪切应变等值云图，软弱结构底部临空部位为剪切高应力区域，软弱结构内剪切应变水平远高于其他位置。当边坡存在软弱结构层（软弱夹层）时，由于其强度较低原因，边坡内应力场重分布将由软弱结构层（软弱夹层）主导，软弱结构层（软弱夹层）率先达到变形条件，边坡内应力场重分布与变形同步进行，至变形直至破坏后，应力场重分布停止。

3.4 破坏机理分析

天然岩体在其漫长的形成过程中，随着时间积累，在缺少外力作用条件下，其自身应力场不断趋于稳定。经过人工开挖或地质活动等外力介入后，形成具有一定的高度和坡度的边坡，原有应力状态被改变，内部应力场进行重新调整分布。

根据第3.2节数值模拟结果表明，假定边坡岩体无软弱结构层（软弱夹层）存在时，坡顶处受到下部岩体的张拉作用，坡顶处主应力为张拉应力，强度控制指标主要为岩体抗拉强度;坡脚处受上部岩体的挤压、剪切作用，其主应力为压应力和剪切应力，强度控制指标主要为岩体抗压、抗剪强度。

当其他条件不变时，岩体边坡存在软弱结构层（软弱夹层）时，边坡稳定性的强度控制指标主要由软弱结构层（软弱夹层）的抗剪切强度水平决定，由于软弱结构层（软弱夹层）强度较低，造成边坡岩体内应力分布不连续，破坏应力从该处释放，从而造成边坡失稳破坏，以滑移式崩塌灾害形式出现。

在实际工程中，边坡失稳破坏的原因错综复杂，是多种原因的耦合作用造成。但究其本质，其破坏机理可概括为：应力场重分布后，破坏应力（张拉、挤壓、剪切等）作用大于边坡岩体的强度时，即进入临界状态或发生失稳破坏。

4 几点认识和思考

（1）边坡稳定性有限元数值模拟分析的结果表明，边坡岩体的应力较大部位为坡顶、坡角及软弱结构层处，当边坡呈现失稳（或临界状态时），上述3个区域应有明显的变形，如：张拉裂缝、挤压裂隙或剪切破碎带等。所以，坡顶、坡角、软弱结构层处的破坏迹象应为勘查工作的重点。

（2）作为定性分析方法、定量分析方法的一个重要补充，有限元法可应用于求解岩质边坡稳定性问题，数值模拟结果可揭示边坡破坏机理和破坏形式，可为边坡稳定性分析和评价提供依据。但在实际工程应用中，在分析模型中选取的参数有别于定性、定量分析法，有限元法需要更为全面、细致的边坡几何、物理力学参数，以满足更加贴近真实的边界条件和耦合条件。

（3）岩质边坡稳定性受内外双重因素影响，内部因素包括结构面的空间分布、岩性强度及强度差异等，外部因素有人类工程活动、风化作用、雨水侵蚀等。在内外双重作用下，岩质边坡工程性质十分复杂。这就需要模型建立过程中对特定的影响因素进行概化处理，优化模型及算法，使得计算结果更加接近于实际情况，这需要大量的经验数据及软件自身算法的优化来实现。

（4）岩质边坡的稳定分析是很复杂问题，相对于广泛应用的定性、定量分析方法，有限元法是一个理论上更为完备的分析方法，但对边坡岩土体的几何参数和物理力学参数有更高的要求。当前的多种工作方法各有利弊，但无高下之分，采用单一工作方法时，不免有失偏颇，出现片面的结论。综合运用多种方法分析，扬长避短，以得到更加客观科学和可靠的结论，更好解决工程问题。

参考文献：

陈祖煜，1998.岩质高边坡稳定分析方法与软件系统[J].水力发电，3（2）：3-5.

谷德振，1979.岩土工程地质力学基础[M]. 北京：科学出版社.

《工程地质手册》编委会，2007.工程地质手册[M].4版.北京：中国建筑工业出版社.

黄来源，2020.北京市突发地质灾害防治策略刍论[J].城市地质，15（1）：63-75.

韩建超，2020.北京地区崩塌监测预警初探：以琉辛路监测路段为例[J].城市地质，15（2）：148-153.

贾三满，翟淑花，姜媛，2017.北京突发地质灾害防控对策[J].城市地质，12（4）：16-23.

潘懋，李铁峰，2002.灾害地质学[M]. 北京大学出版社.

张丽，黄英，任磊，等，2007. 边坡稳定影响因素及稳定分析方法讨论[J]. 云南水力发电，23（4）：22-26.

赵忠海，2009.北京地区突发性地质灾害易发区划及危险度评价[J].资源调查与环境，30（3）：213-221.