基于强化学习的模型选择和超参数优化

吴 佳，陈森朋，陈修云，周 瑞

(电子科技大学信息与软件工程学院 成都 610054)

近年来，机器学习已广泛应用于如机器翻译[1-2]、语音识别[3-4]、图像识别[5-6]和游戏[7]等众多领域。针对某一问题，如何快速构建一个成熟、可靠的机器学习模型就显得尤为重要。为了满足行业需要，使机器学习算法能够得到快速、高效的利用，一大批企业针对普通用户开发出了一些应用系统，如DataRobot.com[8]、BigML.com[9]、Wise.io[10]等。在机器学习算法的应用中，不可避免涉及两个重要问题：算法模型选择和超参数优化。

现有的机器学习算法众多，具有代表性的算法有逻辑回归(logistic regression)、支持向量机(support vector machine)、决策树(decision tree)和随机森林(random forest)等。针对不同的问题，没有一个机器学习算法模型能够适用于所有问题。在同一问题上，不同的方法所达到的性能也存在不同程度的差异。这给机器学习算法的使用者造成了不小的麻烦。算法模型选择成了机器学习算法广泛应用的一大障碍。

另外，超参数优化同样成为了机器学习算法应用中的难点之一。超参数不同于算法模型内部的参数，它是在算法模型训练之前设置的参数。在训练开始之前，往往希望找到一组超参数的值，即超参数组合，使得算法模型可以在合理的时间范围内对某一数据集的分类或拟合达到最佳性能。这个过程被称为超参数优化，它对机器学习算法的性能起着至关重要的作用。在实践中通常需要不断调整超参数的值，最终选择最佳的超参数组合。若算法模型的超参数搜索空间较大，该过程将非常耗时。

因此，针对某一问题(或数据集)，最终结果很大程度上是由机器学习算法模型和算法对应的超参数组合共同决定的。本文提出了一种基于深度强化学习的方法，用于自动实现机器学习算法的选择和超参数的优化。该方法利用长短期记忆(LSTM)网络[8]构建一个智能体(Agent)来代替机器学习使用者选择最优的机器学习算法及其超参数；Agent 在训练集上训练所选择的机器学习算法及超参数组合所对应的算法模型，在验证数据集上验证该算法模型的性能；以在验证集上的准确度作为奖赏值，利用策略梯度算法(policy gradient)[9]优化Agent 的决策。经过多次迭代，Agent 选择出适合该问题的最优模型及对应的超参数。在Agent 训练过程中，梯度方差较大，本文提出引导数据池来解决该问题。本文主要的贡献在于以下3 点：

1) 使用强化学习框架来解决模型选择和超参数优化问题；

2) 提出了数据引导池结构来提高方法的稳定性；

3) 通过在标准数据集上对8 种机器学习算法进行优化，相比于其他方法，本文提出的方法达到了最好的优化结果。

1 相关工作

模型选择和超参数优化问题通常称为CASH(combined algorithm selection and hyperp-arameter optimization)[10]问题。CASH 问题定义如下：

针对某一数据集，寻找使得式(1)的值最小的算法 A∗及相应的超参数配置 λ∗：

为了解决CASH 问题，研究者提出了一系列解决方案，如随机搜索，贝叶斯优化等。随机搜索在算法和对应的超参数构成的搜索空间中随机采样。该方法执行起来效率高且操作简单，经过少量的尝试就可以搜索到性能较好的机器学习算法及相应的超参数的值。但文献[10]表明，随机搜索方法只有在达到或接近最优值的组合的数量占总的组合数量的比重超过5%时，搜索效率较高；其他情况下，随机搜索方法的表现较差，很难搜索到最优值。Auto-WEKA 是一个基于机器学习工具包WEKA[11]的自动化机器学习框架。CASH 问题首先在Auto-WEKA[12]系统中被解决，其核心是贝叶斯优化方法，主要包括基于高斯过程的贝叶斯优化方法[13]，基于模型的顺序算法配置方法(sequential modelbased algorithm configuration, SMAC)[14]及其改进版本的基于树状结构Parzen 的估计方法(TPE)[15]。文献[16]使用热启动技术提升SMAC 的性能。自适应协方差矩阵进化策略(CMA-ES)算法[17]，是基于进化算法的一种改进算法，主要用来解决非线性、非凸的优化问题，在解决模型选择和超参数优化问题也具有很好的效果。最近，BOHB[18]被提出，该方法将贝叶斯优化与HyperBand 方法相结合用于解决模型选择和超参数优化问题，并具有很好的优化效果。上述这些方法存在一定的局限性，如基于高斯过程的贝叶斯优化方法只适用于低维空间的超参数优化问题。在搜索性能方面，基于贝叶斯优化的方法容易陷入局部最优，很难探索出模型性能最好的算法及超参数组合。在时间性能方法，对于拥有较大的搜索空间的问题，贝叶斯优化方法时间效率会大幅降低。

强化学习(reinforcement learning，RL)[19]是从动物学习、参数扰动自适应控制等理论发展而来的。其基本原理是：智能体的行为决策得到环境的反馈，即奖赏值；通过最大化累积奖赏值，以学习到最优的行动策略。通常利用马尔可夫决策过程对强化学习问题进行建模。随着问题复杂度增加，谷歌的人工智能团队将具有感知能力的深度学习和具有决策能力的强化学习相结合，即深度强化学习(deep reinforcement learning，DRL)[20]，成功解决了诸如与人类进行围棋对弈[21]等复杂任务。通过将深度学习与强化学习结合，实现了从感知(perception)到动作(action)的端对端的学习。目前，深度强化学习在视频[22]、游戏[23]、机器人[24]等领域获得广泛的应用。本文利用深度强化学习的优势来解决CASH 问题。

2 模型选择和超参数优化方法

2.1 Agent 模型结构

模型选择和超参数优化可看作一个多阶段决策问题，在每个阶段(时刻)针对某个模型或者超参数做出相应决策，因此不同的时刻产生不同的输出。由于模型以及超参数之间存在相关性，每个阶段的决策又是相互关联、相互影响的。根据上述特点，模型和超参数设置的过程可由一个可变的字符串来表示，利用长短时记忆神经网络(LSTM)构造的智能体来生成这样的字符串，具体优化过程如图1 所示。

智能体以概率P 为选择一组超参数a1:T，其中，动作a1对应选择的机器学习算法；动作序列a2:T表示a1选择的算法模型中超参数的取值。T–1 为a1选择的算法模型中超参数的总个数，不同的机器学习算法T 的取值不同。接下来，在训练数据集上训练智能体选择a1:T所对应的算法模型；以训练好模型在验证集上的准确率作为奖赏值(reward)，利用强化学习中的策略梯度算法来训练Agent。奖赏值引导Agent 在下次迭代中以更高的概率选择准确率高的算法及对应的超参数的值。随着时间的推移，智能体将学会如何针对某一问题(或数据集)自主选择最优的机器学习算法和相关超参数。

本文利用LSTM 网络构造Agent 来自动选择算法模型及超参数组合。该Agent 的网络结构如图2所示，它的核心由3 层LSTM 网络构成，每层拥有35 个神经元节点；输出层由softmax 函数构成；输入层、输出层与3 层LSTM 网络结构之间各有一个全连接层。Agent 中3 层LSTM 网络结构在任意时刻的结构、参数共享。Agent 在不同时刻输出不同的模型/超参数选择，并把不同时刻选择值在候选值中的索引位置作为下一时刻的输入数据，当所有超参数值生成后，Agent 输出停止。Agent 在任意时刻的输出为对某个模型/超参数所有候选值的评估。该值越大，对应的预选值被选中的概率越高；反之，越低。Agent 根据这些评估值做出最优的选择。

2.2 Agent 训练学习

当Agent 以概率P 选择模型/超参数序列a1:T后，将a1:T对应的算法模型在训练数据集上训练至收敛，再在验证数据集上运行得到的准确率作为奖励信号R 来优化Agent 的参数θ，使得随着时间的推移，Agent 学会选择准确率更高的模型/超参数组合。Agent 训练方法采用强化学习算法中的策略梯度[12]，算法的优化目标为最大化期望总奖赏：

式中， P( a1:T;θ)表示表示Agent 输出模型/超参数序列a1:T的概率。

由于优化目标是找到一个参数θ，使得期望总奖赏最大化。根据梯度下降算法，通过求解目标函数的梯度，进而更新参数θ，最终可求得局部最优值：

根据上式，可以看出 ∇θ(J(θ))为 函数∇θlogP(at|a(t−1):1;θ)的期望。本文利用在固定参数θ 下m 次采样的均值作为梯度更新的无偏估计：

式中，Rk为第k 次采样的模型在验证数据集上的准确率；b 为基准值，其值为已采样到的算法模型的准确率的指数滑动平均值。基准值设置的目的在于减小Agent 训练过程中的方差。

2.3 减小方差

虽然策略梯度算法中采用了基准值降低训练中的方差，但Agent 训练过程中仍存在方差过大问题。为了进一步减小方差，提高Agent 决策的稳定性，本文为Agent 添加一个“引导数据池”。具体来说，设置一个大小为m 的数据池，保存到当前时刻性能表现最好的m 条数据，定期把这批数据送入到Agent 中进行训练。这样做起到了一个把握优化方向、防止模型方差过大的作用，故称之为引导数据池。具体算法如下。

输入：无

输出：最优超参数组合

1) 初始化Agent 的模型参数θ;

2) 初始化引导数据池top_data;

3) for i = 1 : (N/m)

4) for j = 1 : m

5) 初始化Agent 的输入数据input 为全1 向量;

6) for t = 1 : T

7) 将t 时刻的输入数据添加进输入数据列表;

8) 将Agent 在t 时刻输出值作为下一时 刻的输入数据;

9) 将t 时刻的选择添加进动作列表actions;

10) end for;

11) end for;

12) 在训练数据集上训练与动作列表actions 对 应的模型，在验证数据上验证模型准确 性，得到奖赏值并存入奖励值列表rewards;

13) 更新引导数据池top_data;

14) if i == 0

15) b = mean(rewards);

16) end if;

17) if (i+1) % n_step == 0

18) 获取引导数据池top_data 中的数据；

19) 利用策略梯度算法更新Agent 的参数θ;

20) else

21) 利用策略梯度算法更新Agent 的参数θ;

22) end if;

23) b=b*r + mean(rewards)*(1-r);

24) end for

其中，N 表示Agent 采样的总批次数(迭代次数)；m 为Agent 更新一次模型参数所需的数据量大小；n_step 为Agent 利用数据引导池中的数据更新模型参数的步伐大小；r 控制着基准值b 的滑动范围。

为了验证引导数据池的有效性，同样对随机森林算法的超参数进行优化实验。在相同的实验环境下，本文进行了共20 次的未添加引导数据池的Agent 与添加了引导数据池的Agent 的对比实验，如图3 所示。实验结果表明，添加了引导数据池的Agent 在18 次运行中都选择到了同一个最优的超参数组合，而未添加引导数据池的Agent 只有1 次选择到了最优的超参数组合。未添加引导数据池的Agent 所存在的高方差、不稳定的问题得到了有效的解决。

3 实验结果及分析

3.1 搜索空间及数据集

根据文献[25]中对179 种机器学习算法在UCI machine learning repository 数据集上的评估结果，本文挑选了一些具有代表性的学习算法以及相应超参数，并为这些超参数设定了一些候选值，详细情况如表1 所示。

UCI machine learning repository 数据集是一种常见的、用于分类任务的数据集。采用两种UCI标准数据集进行测试，数据集信息如表2 所示。数据集的原始数据经过预处理后，将整个数据集分成验证集和测试集两部分，验证集占整个数据集的80%，数据集中剩余的20%的数据将作为测试集，用于测试所选择的超参数组合对应的模型最终的性能。

在构建Agent 的过程中，Agent 采用3 层LSTM，每一层有35 个隐藏节点。采样的总次数N 设置为5 000 次；每次采样的超参数组合的数量m 设置为8；引导池大小设置为8；数据引导池的利用间隔n_step 设置为10；基准值b 的控制率r 设置为0.8；以−0.2～0.2 之间的随机值对Agent 的权重进行初始化，使用Adam 优化器[26]进行策略优化。

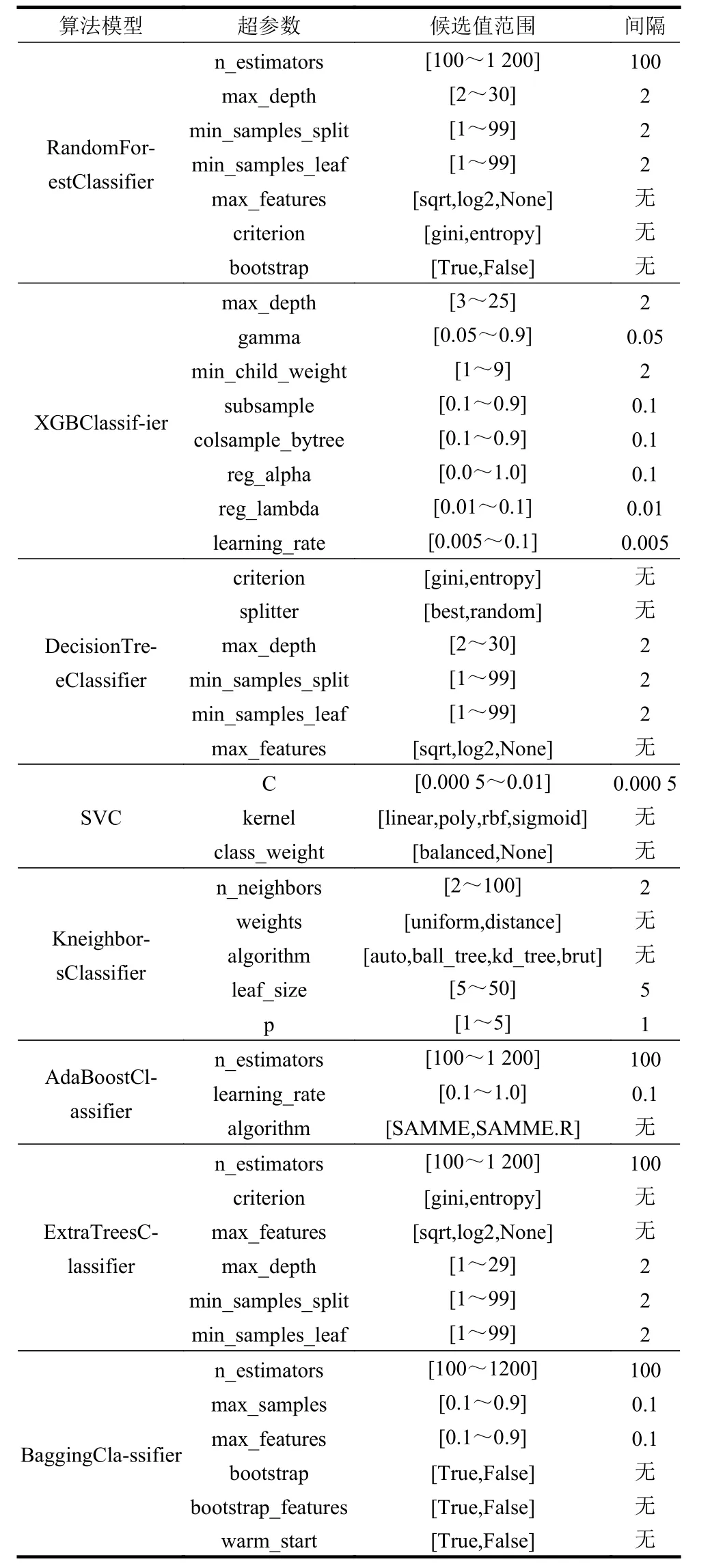
表1 候选算法模型及对应超参数候选值

表2 数据集基本信息

3.2 实验结果及分析

实验在两个UCI 标准数据集下进行，对比了CMAES 优化方法、TPE 优化方法、随机搜索方法的准确度、时间效率、稳定性。实验结果如图4 和表3 所示，所有结果为3 次实验后统计值。图中所示为3 次实验的平均值和1 倍标准差。

图4为优化过程中所有方法的准确度。横轴表示采样次数；纵轴表示每次采样后选择的模型在验证集上的准确率。图中数据为3 次实验的均值和一倍标准差。表3 结果为5 000 次采样完成后，4种方法选择的模型的统计结果(3 次实验平均值)。其中，准确度表示模型在验证集上最高准确率的平均值；耗时为完成3 次训练所耗费时间的平均值，该值大小反应了优化算法的时间性能；标准差为3 次实验最高准确率统计的标准差，该项数据反应了算法的稳定性。

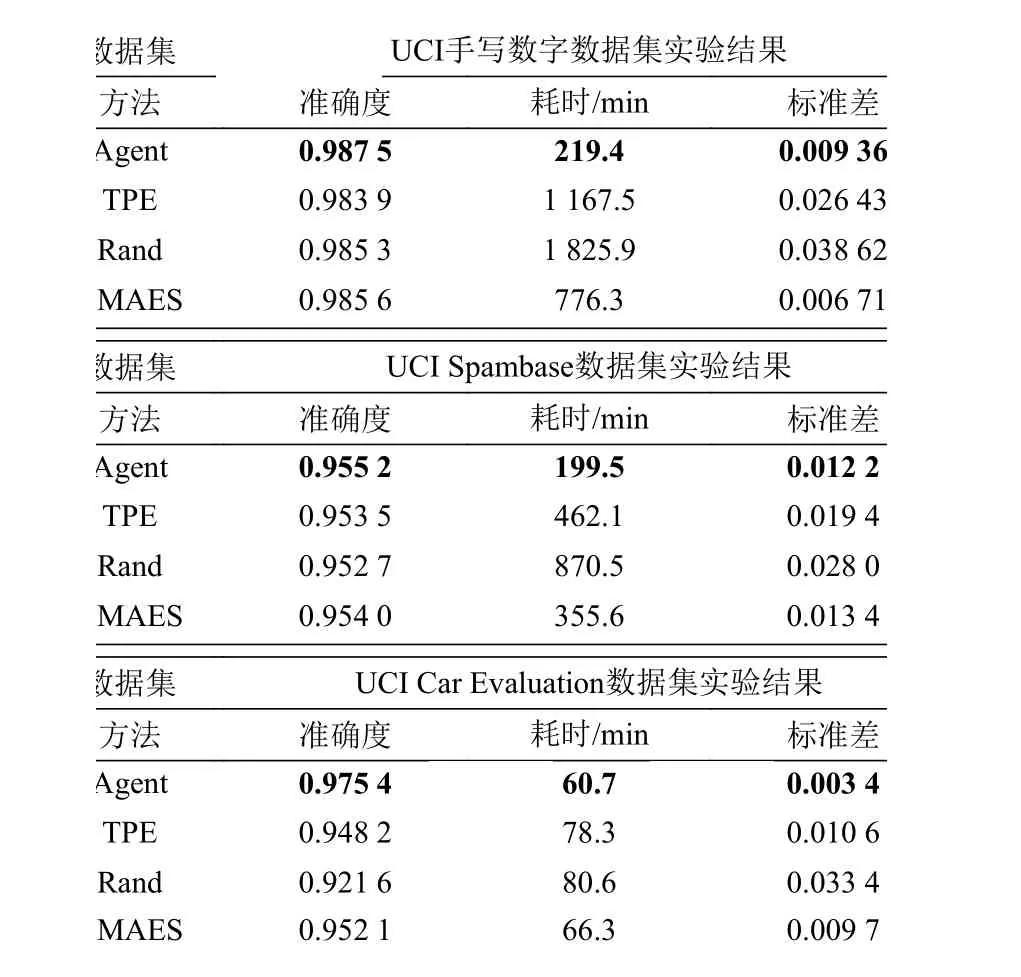
表3 优化结束后统计结果

通过分析实验数据可以看出，本文提出的优化算法能够在最短的时间搜索到最优的结果。虽然随机搜索、TPE 优化方法和CMAES 优化方法也能达到较好的优化结果，相比之下，Agent 能够用远少于前两种方法的时间搜索出更优的算法模型和超参数组合，尤其是在问题规模增大时，Agent 优化方法仍具有很高的时间效率，综合性能更好。TPE 方法使用从开始到当前时刻所有采样的数据进行训练，这就造成了对数据的极大依赖，容易造成过拟合，最终陷入局部最优。相比之下，Agent 在对自身的模型参数进行更新时，每次都是由当前时刻采样到的新数据进行训练，能够搜索到更好最优解。随机搜索算法的搜索效率相比与TPE 算法更低，究其原因在于随机搜索方法的采样具有随机性，随着搜索空间增大，搜索到相同模型超参数组合可能性越小，因而耗费在模型训练上的时间也就越多。通过实验还发现Agent 通过数据引导池结构，相比于TPE 和随机搜索方法能够有效的减小训练时的方差，使训练更加稳定。

4 结 束 语

本文提出了一种基于深度强化学习的超参数优化方法。该方法利用长短时记忆网络构建了一个Agent，针对不同问题(数据集)自动进行算法选择超参数优化。Agent 以最大化模型在验证集上的准确率为目标，以Agent 每次选择的所对应的模型在验证数据集上的准确率作为奖赏值，利用策略梯度算法来修正Agent 的模型参数。经过多次迭代，Agent 最终收敛并选择出最优的算法模型及超参数组合。为了验证算法的可行性和性能，利用Agent对两种标准数据集进行优化实验。通过对比TPE和随机搜索两种具有代表性的超参数优化方法，本文提出的方法在准确率、运行时间效率和稳定性上均优于上述算法，特别是对于规模较大的问题，具有绝对优势，其完成优化所需的时长最低仅约为随机搜索方法的12%和TPE 优化方法的19%。